基于相关性特征选择和LSTM以及正态分布思想的风电机组故障预测
(东方电气新能科技(成都)有限公司,四川德阳 618000)
0 引言
随着我国风力发电的大力推广和平价上网的逐步推行,风电行业尤其是各主机厂,不得不开始关注成本。降本,除了降低制造成本,运行和维护(以下简称运维)成本也是不得不考虑的点。其中,大部件更换成本从几万到上百万不等。受设计、制造工艺以及后期运维质量影响,实际上,大部件的更换频率并不低。
为了降低这部分费用,各大主机厂家、诸多高校和一些业主都在进行故障早期预警相关的研究。如,刘轩的《风力发电机温升故障预警方法研究》[6]、陆超的《基于EEMD-PCA的风电轴承故障预警方法》[7]等。在基于SCADA数据进行的研究方面,大数据、神经网络等技术均得到相关应用,如文献[2,8]。刘轩的《风力发电机温升故障预警方法研究》提出了一种加权主成分分析法,解决了传统主成分分析法没有考虑各主成分的权重问题。但没有考虑到,温度转速等模拟量并非0-1这样的状态量,即没有考虑时间累加效应。此外,分类算法在故障识别中也得到大量应用,如文献[9-10]。然而,分类算法依赖大量可靠的标记样本,这样的样本并不容易大量获取。这无疑增加了实现的难度。因此,本研究将在已有研究基础上,从实际应用的角度,提出一种结合相关性分析、长短期记忆及正态分布思想的风力发电机故障预测解决方案,并进行实际应用。
1 数据获取与预处理
1.1 数据获取
为方便验证预测方案的有效性,应选择发生过主要部件(如主轴承)温度异常机组从故障时刻(包含)往前一个月的数据以及该机组此前稳定运行期间至少一年的数据。数据的粒度为10分钟一个点。
1.2 数据预处理
SCADA数据在产生和存储过程中均可能异常。如,传感器松动极易产生瞬间极大值。因此,必须对极端数据进行清洗。首先求得每一维数据的上下四分位数,再通过四分位数求得上下边界,完成对异常数据的清洗。公式如下:

其中,k∈[1.5,3],与数据的集中程度有关,这里我们取k=1.5。upq,lowq分别是排序后的上下四分位数。uplimit,lowlimit是求出的上下边界,即合理的数据应在上下边界内。对边界外的数据进行剔除。
2 特征处理
2.1 基于经验的初步筛选
一台机组上的传感器有几十到上百个,数据就可能达到上百维。输入维度过大不仅会导致模型过大,同时还会造成精度下降。因此,必须进行有效的特征选择。首先,基于经验[11]选取针对具体部件温度的相关性较大的若干维度数据。假设要监测的部位是主轴后轴承,根据经验,我们可以大致选出风速、功率、环境温度、机舱温度、转速、主轴前轴承温度这些相关量。
2.2 相关性特征选择
再利用相关性分析对上一步选取的经验维度进行进一步的分析,实现进一步降维。相关性计算采用的是皮尔逊相关系数。

图1中,区域颜色越蓝,表示两两相关性越强。由图1可知,与主轴后轴承温度相关性由强到弱的量分别是前轴承温度->机舱温度->环境温度->转速->功率->风速。显然,我们应首先剔除风速这个最不相关的变量。

图1 输入数据各维度相关性Fig.1 Correlation of various dimensions of input data
此外,环境温度和机舱温度存在很强的相关性,并且,轴承的直接外环境是机舱,因此,我们可以进一步剔除环境温度这一变量。最后,基于实际应用场景,我们对前后轴承均需要实施监测。因此,前后轴承温度不宜作为彼此输入参数。针对主轴后轴承温度,我们最终使用机舱温度,功率和转速作为输入数据。
2.3 归一化
由于各输入数据的数值范围差异较大,因此,有必要进行归一化处理。归一化能加快收敛速度,在一定程度上能提高模型精度。由于数据基本满足正态分布,本项目采用的是均值方差归一化。
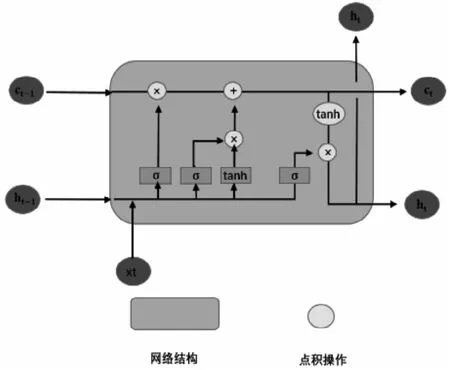
图2 LSTM 网络结构示意图Fig.2 Schematic diagram of LSTM network structure

3 使用LSTM网络训练模型及验证
3.1 模型构建
长短期记忆(Long Short-Term Memory),简称LSTM。是在循环神经网络(Recurrent neural Network)的基础上,增加了时间序列上各时刻数据的不同权重。解决传统循环神经网络梯度可能会消失的问题。(如图2)
本文使用多层LSTM,输入为前文确定的机舱温度、功率、转速,输出为主轴后轴承温度。使用数据为贵州遵义某风场11#机组历史运行数据,选择2019年全年数据作为训练和测试样本。使用参数搜索算法,设定网络层数在2~12层之间,初始学习率0.0005~0.01之间,优化控制器采用Adam和SGD,随机生成8组参数组合。最终发现,在本问题下,最佳网络层数为4层,最佳学习率为0.001,优化器Adam比SGD更容易收敛。
3.2 模型验证
该机组在7月14日由监控系统发出主轴后轴承高温报警信号,温度超过设定限制50℃。因此,选择2020年5月至7月16日数据作为验证集。
理论上,在给定工况下,部件温度应该符合某一正态分布。进而,实际值与预测值(理论值)的差值(以下简称残差)也应符合正态分布。图3为训练集上残差分布直方图。
由图3可知,实际残差基本符合均值为0的某一正态分布。基于小概率事件基本思想[3],通过查概率表可知,残差落在(μ-3σ,μ+3σ)以外的概率小于千分之三,残差落在(μ-2σ,μ+2σ)以外的概率小于百分之三。这里,我们只关心温升,即实际值超过理论值。因此,将μ+2σ作为初级预警线,将μ+3σ作为严重警告线。

图3 训练集上残差分布直方图Fig.3 Histogram of residual distribution on the training set
使用训练好的模型预测理论温度值,并计算实际值与健康值之间的残差。绘制残差曲线,如图4。
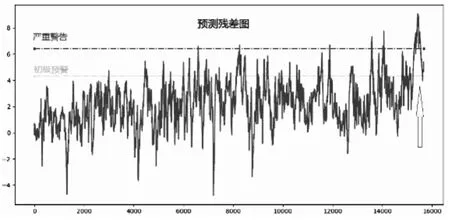
图4 测试集上残差随时间变化曲线Fig.4 The residuals on the test set change with time
从图中可以明显看出故障发展的趋势。早期残差基本处在“初级预警”线下,即实际数据和理论健康数据很接近。后期逐渐突破“初级预警线”(黄色),直至突破“严重警告线”(红色)。同时,可以看到,使用此模型可以让我们提前两三个月发现故障趋势。(图中红色箭头所指位置为实际故障报警时刻)
4 应用与展望
4.1 应用
基于此方法,我们快速搭建了模型批量训练的平台。开发了基于实时数据采集、预警的软件,并配套开发了可视化界面。目前已在超过5个风场部署运行,界面示如图5。

图5 产品应用某界面Fig.5 A certain interface of product application
4.2 总结
提出了一种基于经验和相关性分析的特征选择方法,一种结合循环神经网络和正态分布的小概率事件思想的故障早期预测方法。并在此基础上,对方法进行了实际应用。
4.3 展望
本项目未针对时间序列的长度对预测准确性的影响展开研究。在兼顾高效性能的前提下,寻找这一长度值。
此外,在理论上,训练集为机组健康状况下运行数据。相近环境中的相同机型应可以共用模型。以上两点值得进一步研究。

