基于投入产出技术的吉林省产业关联分析

王雨薇 王静 邓拓

【摘  要】论文介绍了投入产出表及投入产出模型，从直接消耗系数矩阵引出完全需求系数矩阵，利用完全需求系数矩阵计算各产业部门的影响力系数与感应度系数，之后利用2017年吉林省地区投入产出表，计算了吉林省各行业的影响力系数与感应度系数，同时根据影响力系数与感应度系数对吉林省各行业进行了分类，在此基础上，分析各类行业在吉林省经济结构中的作用与地位。

【Abstract】This paper introduces the input-output tables and input-output model， derives the complete demand coefficient matrix from the direct consumption coefficient matrix， and uses the complete demand coefficient matrix to calculate the influence coefficient and induction coefficient of each industrial sector. After that， the paper uses the input-output table of Jilin Province in 2017 to calculate the influence coefficient and induction coefficient of various industries in Jilin Province， and classifies various industries in Jilin Province according to the influence coefficient and induction coefficient. On this basis， the paper analyzes the role and position of various industries in the economic structure of Jilin Province.

【关键词】投入产出;产业关联分析;吉林省

【Keywords】input-output; industrial association analysis; Jilin Province

【中图分类号】F127                                             【文献标志码】A                                                 【文章编号】1673-1069（2021）10-0066-04

1 引言

国民经济运行过程中，在各产业之间总有一定的投入产出关系，即某一部门的产出是另一部门的投入，这样就构成了整个经济系统的投入产出关系。由美国经济学家里昂惕夫提出的投入产出技术，已成为现代产业关联分析的重要方法，其数学模型的表现形式有投入产出表和投入产出数学模型。投入产出表可以展现经济系统中各部门的投入来源与产出流向的平衡表。投入产出模型则是在投入产出表的基础上建立起来的，运用数学符号表达的各产业之间的数量联系。

2 投入产出分析基本原理

在国民经济运行中，各产业部门产出的产品和服务都被哪些部门消耗和使用了，这些都可以被投入产出表完整地展示出来，而各类产业部门对其他产业部门的产品消耗关系则可以通过投入产出模型来表达。

2.1 投入产出表

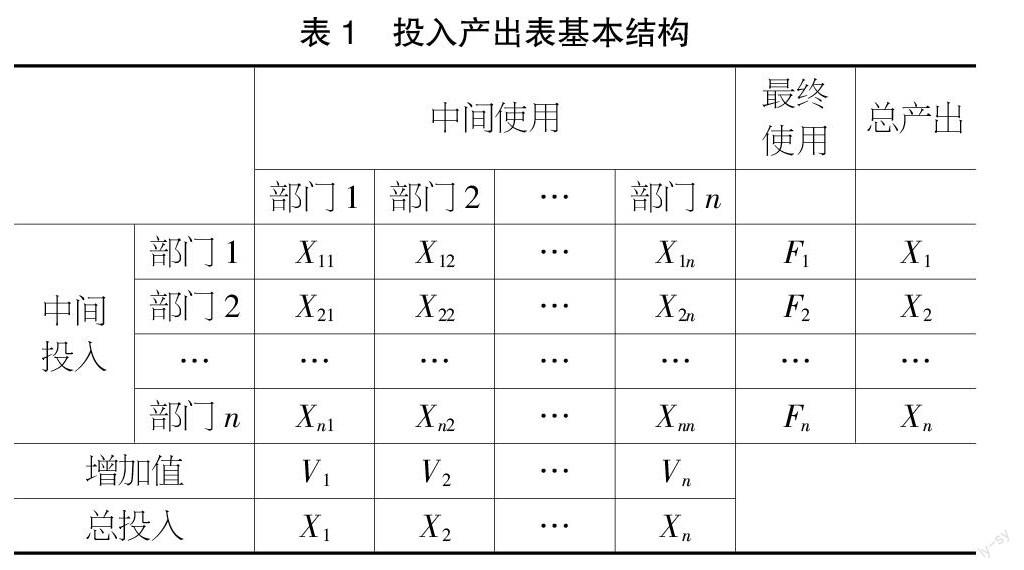
投入产出表最开始引入的是实物型投入产出表，而实物型投入产出表的单位不统一，在建立行向和列向关系时考虑因素较多，对于各产业部门之间的投入产出关系表现度较差。而价值型投入产出表统一了全表的计量单位，克服了实物型投入产出表的缺点，对于产业部门之间的关联关系具有更强的表现能力，同时，在价值型投入产出表的基础上的数学模型更加丰富，可以方便地推导各类产业间的关联系数。价值型投入产出表可以发挥出比实物型模型更广泛的内容和作用，因此，本文主要利用价值型投入产出表进行分析。价值型投入产出表的基本表现形式如表1所示，该表以整个国民经济系统作为描述对象，将其作为一个经济系统，各产业部门成为系统中的各个要素，采用表格形式表达了各产业部门间的投入产出关系。由于价值型投入产出表中的数据统一使用货币作为计量单位，表格中的行向数据与列向数据都可以加总。随着计算机技术的发展，投入产出模型的求解变得十分方便，投入产出技术也得到了十分广泛的应用。

假设表中包括n个部门，则：

Xij表示在经济系统中，j部门消耗i部门产品或服务的价值;

Fi表示i部门产出的产品或服務被最终使用消耗的价值;

Xi表示i部门在经济系统中产出产品或者服务的总价值;

Vj表示j部门在经济活动中一共创造的增加值。

2.2 投入产出模型的基本假定

投入产出表的数据是可计算一般均衡模型的基础，因此，一般均衡理论的假设条件也适用于投入产出模型，另外，为了可以很好地运用投入产出模型，投入产出分析还有3个基本假定。

①“纯”部门（同质性）假定。各产业部门生产技术与投入结构单一，产品同质。该假定也可以理解为，产业部门内的产品可以完全替代或按比例生产，产业部门之间的产品不具有替代性。

②直接消耗系数稳定性假定。某一定时期内直接消耗系数不发生变化，包括了2个方面：一是直接消耗系数不随时间改变;二是直接消耗系数在同一产业部门内的各企业之间保持不变。

③比例性假定。经济系统中各产业部门的产品的产出与投入呈现不变的正比例关系。

在3个基本假定中，“纯”部门假定是最重要、最核心的假定，有了这个假定，投入产出分析便可以采用线性的分析方法。其他2个假定则是为了简化模型分析过程中的复杂性。

2.3 投入产出模型

投入产出表可以从行、列2个方向建立平衡关系。表格的横向表示对应的产业部门的产品流向哪些纵向部门，流入各部门产品价值和等于总产出，即：中间使用+最终使用=总产出。列向数据表示产品生产中的各种投入要素，包括固定资产折旧、劳动者报酬、生产税净额和营业盈余等，这些要素的价值量之和等于总投入，即：中间投入+增加值=总投入。按行建立的数学关系式为：

Xi=（Xi1+Xi2+…+Xin）+Fi=Xij+Fi

按列建立的数学关系式为：

Xj=（X1j+X2j+…+Xnj）+Vj=Xij+Vj

利用投入产出表可以计算每生产单位j部门的产品，要耗费i部门产品的数量，并将其定义为直接消耗系数，公式表达为：

aij=

直接消耗系数是投入产出分析中的最基本消耗系数，也是其他系数的计算基础，其大小表示产业部门之间直接联系的紧密程度。

用矩阵形式表示a、F以及X如下：

A=，F=，X=

则行方向的投入产出模型用矩阵形式可以表示为：

X=AX+F

整理后得到：

F=（I-A）X，X=（I-A）-1F

式中：I为单位矩阵，B=（I-A）-1为里昂惕夫逆矩阵，也称完全需求系数矩阵。

2.4 影响力系数与感应度系数

直接运用投入产出表可以计算出直接消耗系数，然而各产业之间还有间接的投入与消耗，这样就需要计算完全需求系数，通常利用投入产出表计算出完全需求系数矩阵，然后运用完全需求系数矩阵计算影响力系数和感应度系数，其中，影响力系数主要通过衡量某产业部门对其他各产业部门产品的需求量，来反映该部门对于整个国民经济的拉动作用。各类部门的产出增加对其他部门的产品需求量大小不同，对于产品需求量大的部门，对社会经济的拉动作用大，影响力系数反映了这个拉动作用的大小。一般利用完全需求系数矩阵某一列的和与所有列和的平均值的比值来计算影响力系数。

Rj=，i=1，2，…，n;j=1，2，…，n

式中，Rj为影响力系数，衡量了j部门增加单位产品所需要投入与各部门增加单位产品所需要投入的对比关系，bij为B=（I-A）-1里昂惕夫逆矩阵中的元素。

Rj反映j部门增加单位最终产品对经济系统中各产业部门投入的需求程度，即对于国民经济各产业部门的拉动程度。当Rj>1时，说明j部门增加单位的最终产品对国民经济中各部门的需求量大于各部门的平均水平;当Rj<1时，说明j部门增加单位的最终产品对国民经济中各部门的需要量小于各部门的平均水平。可知，影响力系数越大，j部门对国民经济的拉动作用越强。

感应度系数主要是通过衡量各产业部门均增加单位产品对该部门产品的需求量，来反映该部门对于整个国民经济的支撑作用。一般来讲，如果社会各产业部门均增加一单位产品，对某部门的产品需求量大则说明该部门对国民经济的支撑作用强，反之亦然。感应度系数就反映了对国民经济支撑作用的大小。一般利用完全需求系数矩阵计算某一行的和与所有行和的平均值的比值的方式来计算感应度系数。

Si=，i=1，2，…，n;j=1，2，…，n，

式中Si为感应度系数，衡量了各部门均增加单位产品的条件下，i部门的投入与各部门投入平均值的比值。

当Si>1时，表明全社会各部门均增加一个单位的产品的使用，对i部门投入的需求量大于各产业部门的平均水平;当Si<1时，表明国民经济各部门均增加一个单位的产品的使用，对i部门投入的需求量小于各部门的平均水平。

利用影响力系数和感应度系数从不同侧面反映了各产业部门在国民经济中的地位。一般认为，影响力系数较大的产业是国民经济中的“支柱产业”，而感应度系数较大的产业则为“基础产业”。

3 吉林省产业关联分析

3.1 各部门的产业关联度

根据《中国地区投入产出表-2017》中吉林省2017年42部门投入产出表，计算各行业的影响力系数和反应度系数并排名，计算结果如表2所示。

从影响力系数和感应度系数计算的结果可以看出，2017年吉林省地方经济的10个重要的“支柱产业”分别为“其他制造产品和废品废料”“专用设备”“通用设备”“电气机械和器材”“非金属矿物制品”“造纸印刷和文教体育用品”“金属制品”“金属冶炼和压延加工品”“交通运输设备”“电力、热力的生产和供应”。10个重要的“基础产业”分别是“金属冶炼和压延加工品”“金融”“金属制品、机械和设备修理服务”“租赁和商务服务”“交通运输、仓储和邮政”“批发和零售”“农林牧渔产品和服务”“电力、热力的生产和供应”“化学产品”“金属矿采选产品”。

3.2 各部门关联交叉分析

根据影响力系数和感应度系数大小（是否大于1），对各部门进行分類，形成以下42个部门的产业关联结果（见表3）。

第一类：影响力系数和感应度系数均小于1。这类部门对国民经济的拉动力较弱，同时对国民经济的支撑作用也不强。从分类结果可以看出，吉林省该类产业部门以第三产业为主。

第二类：影响力系数小于1且感应度系数大于1。从分类结果可知，吉林省这类产业包括6个部门，第三产业仍占据较多的席位，该类产业部门对国民经济的拉动能力较弱，但是，对于国民经济具有一定的支撑作用，经济快速发展时期，该类产业也有可能成为经济发展的瓶颈，也不能完全忽视该类产业的发展。该类部门应归于拉动力弱、制约性强的部门，具有一定的产业关联性。

第三类：影响力系数大于1且感应度系数小于1。从分类结果可知，吉林省这类部门共有17个。这类部门对国民经济需求的拉动力较大，地方经济的快速发展需要此类产业的拉动，因此，应稳定和促进该类产业的发展。同时，这类产业的感应度系数较小，因而受经济需求压力较小，一般是国民经济中较为成熟的产业。该类部门应归于拉动力强、制约力弱的部门。

第四类：影响力系数和感应度系数均大于1。这类部门具有拉动力强、制约力强的双重性质，这类产业包括“金属冶炼和压延加工品”“金属制品、机械和设备修理服务”“电力、热力的生产和供应”“化学产品”“金属矿采选产品”“造纸印刷和文教体育用品”“食品和煙草”7个产业部门。他们是拉动国民经济发展关键的支柱产业，是政府应予以大力支持的产业。

4 结语

根据吉林省产业关联分析结果可知，“文化、体育和娱乐”“餐饮和住宿”“教育”“房地产”这些部门对国民经济没有较大的拉动力，而且，部门自身也不易受到整个经济的拉动，是关联效果（后向关联和前向关联）最低的产业。因此，2020年这些行业受到疫情冲击，但对吉林省经济的总体影响不大。

“租赁和商务服务”“批发和零售”“交通运输、仓储和邮政”“金融”这4个行业为第二类行业，影响力系数小于1，感应度系数大于1，这4个部门对国民经济的拉动不大，虽然感应度系数大于1，但这4个行业中除“金融”行业外，均为劳动密集型行业，对国民经济的约束性较低，因此，2020年这3个行业受到疫情影响也不会对经济整体运行造成较大的影响。

“有色金属冶炼及压延加工业”“化学原料及化学制品制造业”这2个行业为第四类行业，对经济的拉动作用较强，同时也是受到经济的影响，2个行业的影响力系数排名分别为8和23，对经济的影响能力有限。在前面提到的“制造业”由于其范围比较广，没有纳入行业之中，通过吉林省产业关联分析，影响力系数前十位的行业“其他制造产品和废品废料”“专用设备”“通用设备”“电气机械和器材”“非金属矿物制品”“造纸印刷和文教体育用品”“金属制品”“金属冶炼和压延加工品”“交通运输设备”“电力、热力的生产和供应”中，绝大部分为“制造业”范畴之内，这些行业是对吉林省经济拉动较强的行业，应密切关注。

【参考文献】

【1】刘起运，陈璋，素汝劼.投入产出分析[M].北京：中国人民大学出版社，2006.

【2】董晓明.河北省产业结构研究与主导产业选择[D].沈阳：辽宁大学，2014.

【3】余倩.我国产业关联度分析[J].对外经贸，2014（08）：72-74.

【4】郭富.基于产业关联的东北区域发展研究[D].哈尔滨：哈尔滨工业大学，2016.