二维正交各向异性位势问题的高阶单元快速多极边界元法1)

李 聪 胡 斌 胡宗军 牛忠荣

∗(安徽建筑大学土木工程学院,合肥 230601)

†(合肥工业大学土木与水利工程学院力学系,合肥 230009)

引言

相较于有限元法(FEM),边界元法[1](BEM) 只需在结构外边界划分网格,因此BEM 可对复杂几何模型进行简单的网格划分.然而BEM 生成的系数矩阵是非对称满阵,构造矩阵所需的运算量级为O(N2),如果采用高斯消去法求解,则所需运算量级更是达到O(N3),因而导致BEM 难以计算大规模问题.伴随快速多极算法[2-3]发展起来的快速多极边界元法(FMBEM)可很好地解决这个问题,其所需的运算量和存储量较传统BEM 大大降低,FM-BEM 成为近20 年边界元领域的热门课题之一,并被广泛应用于二维位势和弹性问题、三维声场问题等.

有关快速多极边界元法的研究和应用起源于20世纪90 年代初,主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4-6],而后被广泛应用于二维[7-14]、三维[15-22]问题中.Pierce 等[10]采用二维实数域的Taylor 展开格式,实现了O(NlogN)量级的用于二维弹性力学问题的多极边界元法.Liu 等[11]将快速多极算法与对偶边界元法相结合,模拟了二维线弹性多裂纹扩展路径.吴清华[12]将快速多极算法和高振荡积分方法相结合,求解了一类带高振荡Hankel 核的边界积分方程,求解结果和传统方法吻合较好,计算效率也得到大幅度提升.Nishimura 等[19]采用分段常值形函数去离散裂纹问题的超奇异边界积分方程,然后耦合快速多极算法和GMRES 法求解三维裂纹问题.赵丽滨等[20]利用Taylor 级数将三维弹性静力学边界积分方程的核函数进行展开,引入快速多极算法应用于薄体结构问题.Zhang 等[22]耦合了快速多极算法和混合边界元节点法(Hybrid BNM),并将该方法成功应用于三维位势问题的求解.Wang等[21]耦合快速多极边界元法和重复相似子域法,构造出含夹杂的复合材料结构的预处理技术,对三维复合材料进行了大规模的数值模拟.

目前,快速多极边界元法大多采用常值单元,其优点是所有的近场积分,包括奇异积分和几乎奇异积分[23-26]均可采用解析公式直接计算,但对于曲线边界和复杂物理场,常值单元的计算只能依赖于使用大量单元,且计算精度和计算效率往往不能令人满意.使用高阶单元能够获得更准确的计算结果,但由于存在奇异积分和几乎奇异积分的计算难题[27-28],因而鲜见高阶单元快速多极边界元法的相关报导.本文在复平面内计算高阶单元的奇异积分和几乎奇异积分,建立高阶单元快速多极边界元法,并将其应用于二维正交各向异性位势热传导问题分析.

1 二维位势问题的常规边界积分方程

考虑二维正交各向异性材料位势问题,见图1.内点y的位势ϕ(y)可由边界位势ϕ(x)和法向位势梯度q(x)的积分形式表达

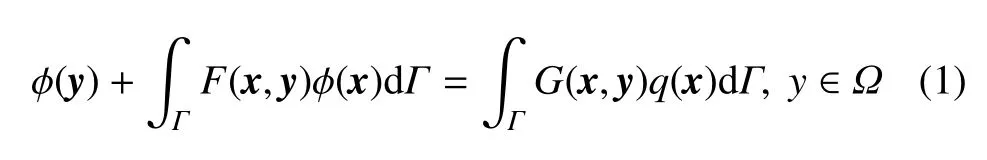
式中,x(x1,x2)称为场点,y(y1,y2)为源点.当源点y落在边界Γ 上,可得二维正交各向异性位势问题的边界积分方程

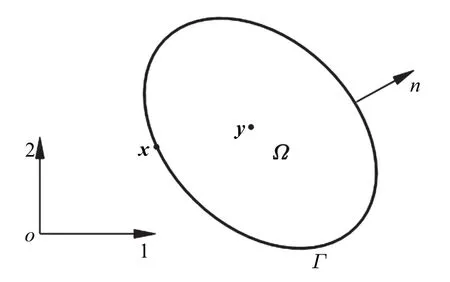
图1 正交各向异性材料位势问题Fig.1 Potential problems of orthotropic materials

其中,c(y)=α/(2π),α 为源点y处边界的内折角.位势G(x,y)和位势梯度F(x,y)的基本解为

当源点y与积分单元Γe的节点重合,式(7) 的积分核是奇异的.当源点y临近积分单元Γe,式(7)和式(8)的积分核呈现出几乎奇异性.相较于奇异积分,高阶单元几乎奇异积分的计算更加复杂.为了尽可能减少处理高阶单元奇异和几乎奇异积分所带来的计算量负担,在复数域内建立高阶单元奇异和几乎奇异积分的计算列式.

2 复势法计算高阶单元奇异和近奇异积分

图2 复平面坐标转换Fig.2 Complex plane coordinate conversion

式中,Re[···]和Im[···]分别表示复变函数的实部和虚部.

2.1 线性单元

对于线性单元,如图3 所示,z1,z2是单元首、末节点复数坐标.在单元局部坐标系oξ 下有

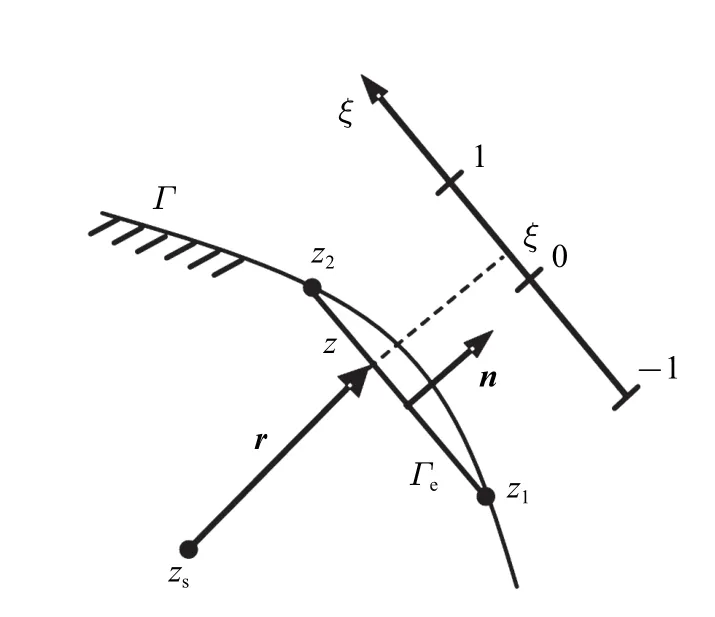
图3 线单元坐标变换Fig.3 Coordinate conversion of a linear element

2.1.1 奇异积分

2.1.2 非奇异积分和几乎奇异积分

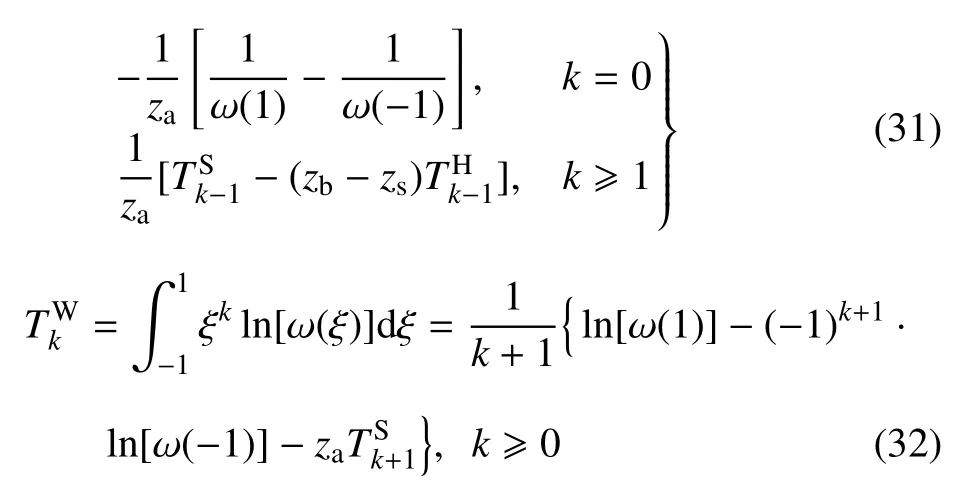
2.2 3 节点二次单元

对于3 节点二次单元,如图4 所示,z1是单元首节点的复数坐标,z2是单元中节点的复数坐标,z3是单元末节点的复数坐标.在局部坐标系oξ 下有

注意到在使用二次单元模拟直线边界时,za可能等于0.因此,二次单元边界积分的计算分为za=0 和za0 两种情形.

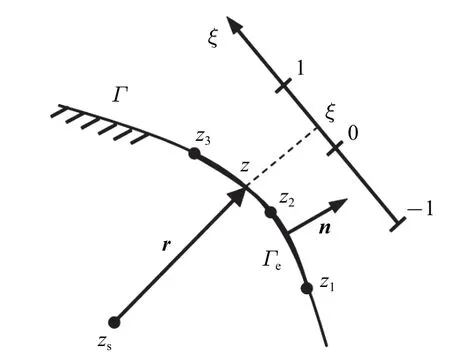
图4 二次单元坐标变换Fig.4 Coordinate conversion of a three-node quadratic element

2.2.1 情形Iza0

(1)奇异积分

当源点zs与积分单元首节点z1重合,使用ξ=2η −1 变换可得

式(41)等号右边第1 项采用常规Gauss 数值积分计算,第2 项采用对数型Gauss 数值积分计算.

当源点zs与积分单元中节点z2重合

式(42)等号右边第1 项采用常规Gauss 数值积分计算,后2 项采用对数型Gauss 数值积分计算.

当源点zs与积分单元末节点z3重合,使用ξ=1 −2η 变换可得

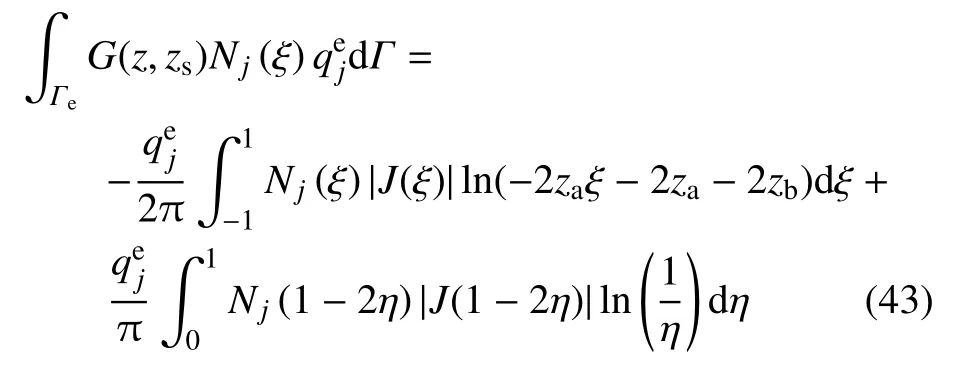
式(43)等号右边第1 项采用常规Gauss 数值积分计算,第2 项采用对数型Gauss 数值积分计算.

(2)非奇异积分和几乎奇异积分

当源点zs位于积分单元外

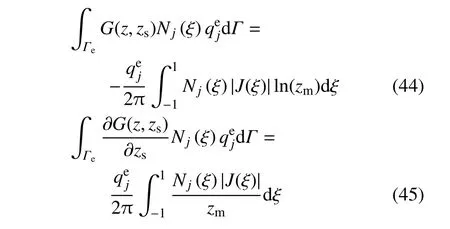
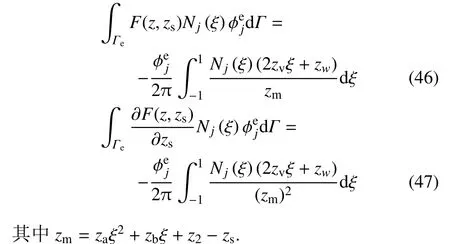
二次单元坐标变换的雅可比|J(ξ)|是根号下ξ 的二次多项式.根号的存在使得式(44)和式(45)难以处理.因此,将|J(ξ)|在ξ=0 处进行泰勒展开

式(49)和式(50)等号右边第1 项的奇异性已然去除,可采用常规的Gauss 数值积分计算.式(49)和式(50)等号右边第2 项与式(46)和式(47)的积分项可归纳为以下几种

2.2.2 情形IIza=0

当za=0 时,如图5 所示,式(32)变成

坐标变换的雅可比|J(ξ)| 和单元单位法向量n(ξ) 均为常量,此时单元是几何线性的,奇异和几乎奇异积分的计算可参考线性单元.

至此,线性单元和二次单元近场积分的计算已在复平面内完成.值得指出,复平面的使用极大地简化了积分的计算公式,这为高阶单元应用于快速多极边界元法提供了便利.

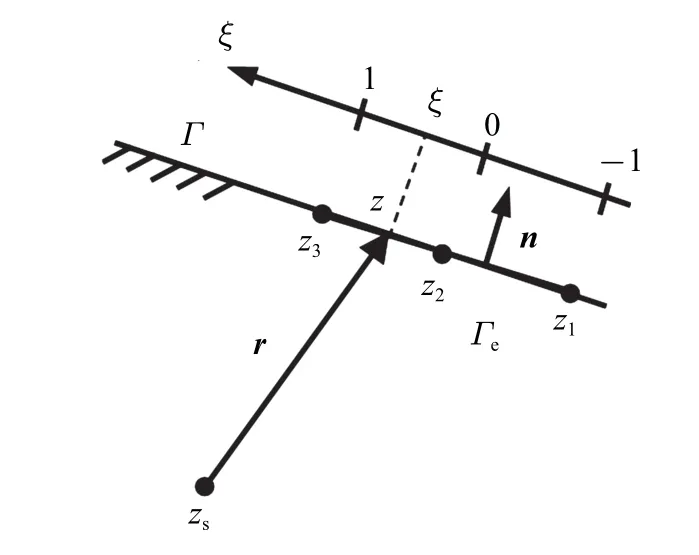
图5 二次单元直边界Fig.5 Three-node quadratic elements modelling the straight boundary

对于二维问题,快速多极边界元法利用四叉树结构将源点y对边界单元的积分分成近场积分和远场积分.以图6 为例,若源点位于cellC内,可将与cellC有公共角点的cell 称之为“邻居”.源点对于cellC及其“邻居”内的边界单元的积分是近场积分,采用本文建立的算法处理.而源点对于剩余的边界单元的积分是远场积分,采用快速多极展开式计算.有关快速多极展开式的计算过程这里不再阐述,详见文献[29].通过方程(2)求得所有未知的边界位势和位势梯度后,域内任意点的位势和位势梯度由式(1)和式(6)算得.

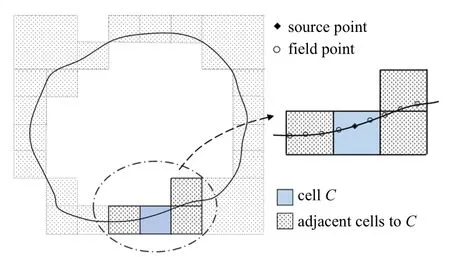
图6 “近场积分”和“远场积分”Fig.6 “The near-field integrals”and“the far-field integrals”

3 算例

为验证本文建立的高阶单元快速多极边界元法的计算精度和计算效率,分别采用常值元快速多极边界元法(FM-BEM-C)、线性元快速多极边界元法(FM-BEM-LA)、二次元快速多极边界元法(FM-BEMQSA)和二次元常规边界元法(CBEM)计算了正交各向异性不规则闭域、圆环闭域热传导问题和随机多孔方板问题.

3.1 正交各向异性不规则闭域热传导问题

不规则闭域的外边界为

情况1:当传热系数ς1=ς2时,各向同性问题.分别采用FM-BEM-C,FM-BEM-LA 和FM-BEM-QSA对图7 结构进行计算,计算结果见表1.

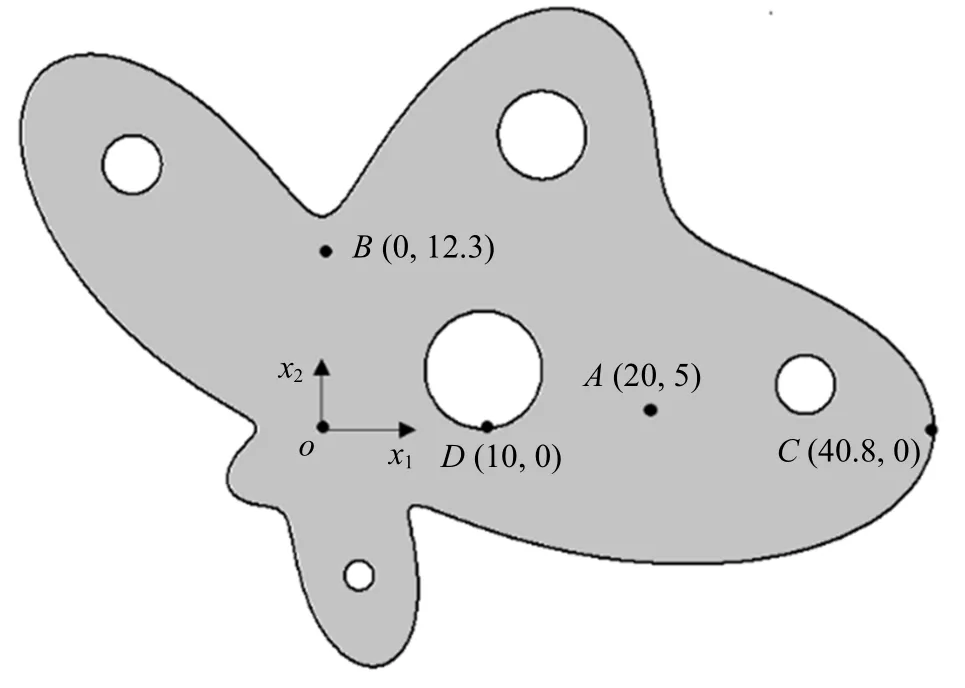
图7 不规则闭域热传导问题Fig.7 Heat conduction in an irregular domain

表1 不规则闭域A、B 点的温度ϕTable 1 The temperatures of inner points A and B in an irregular domain

表1 显示,若边界单元总数n定值,与精确解相比,FM-BEM-QSA 的精度最高,FM-BEM-LA 次之,FM-BEM-C 最差.当n=12 960 时,B点FM-BEM-C的温度ϕ 计算值较解析解的相对误差为0.77%.然而,在n=3240 时,FM-BEM-LA 的计算值较解析解的相对误差为0.15%;在n=1620 时,FM-BEM-QSA 的计算值较解析解的相对误差已小于0.12%.显然,高阶单元FM-BEM 的计算精度和计算效率较FM-BEM-C大幅度提升.

情况2:当传热系数ς1=3,ς2=2,正交各向异性问题.沿外边界均匀划分2880 个单元,沿内边界均匀划分720 个单元.采用FM-BEM-QSA 和FM-BEMLA 计算边界C.D点附近的温度ϕ 和温度梯度qx2,如表2 和表3 所示.

表2 和表3 的结果显示,FM-BEM-LA 和FMBEM-QSA 计算外边界C.内边界D点附近的温度ϕ、温度梯度值q与解析解吻合得很好,FM-BEM-QSA的计算结果更优.实际上,当内点十分接近外边界C.内边界D点时,近边界点温度的计算涉及高阶单元的几乎强奇异积分(1/r),温度梯度的计算更是涉及几乎超奇异积分(1/r2),计算难度较大,但本文第2 节建立的正则化算法能够很好地处理这些积分.

3.2 正交各向异性椭圆环闭域热传导问题

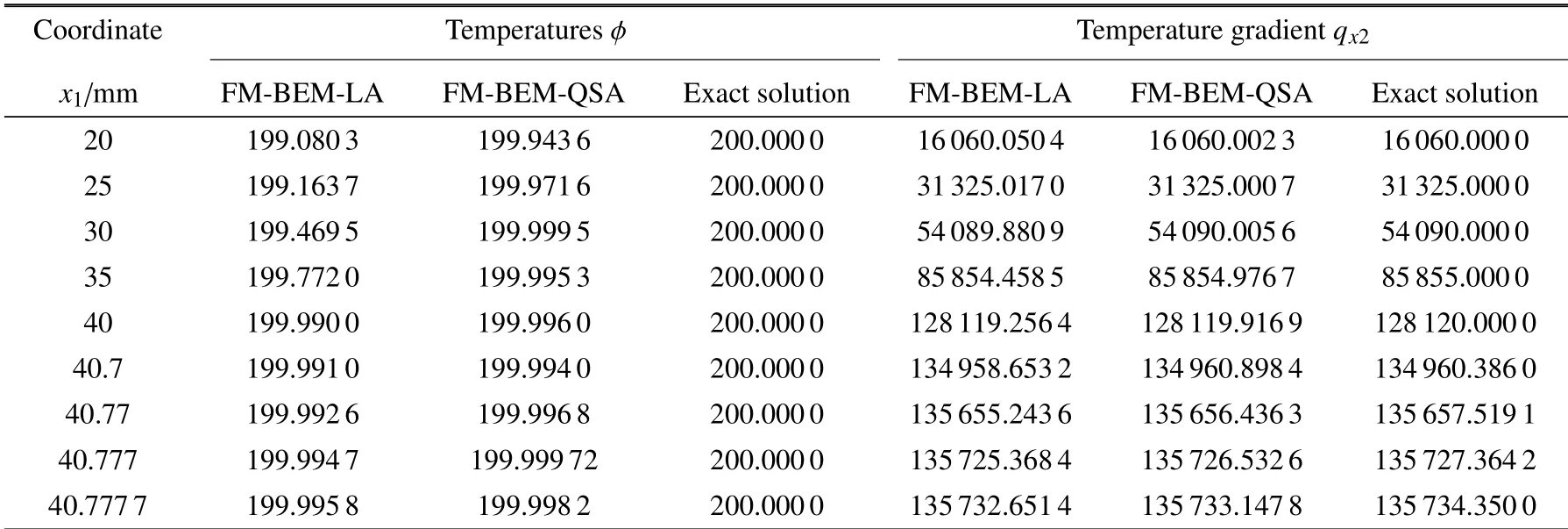
表2 正交各向异性不规则闭域C 点附近沿x2=0 mm 内点的温度ϕ 和温度梯度qx2Table 2 Temperature and temperature gradient of inner point near point C(x2=0 mm)

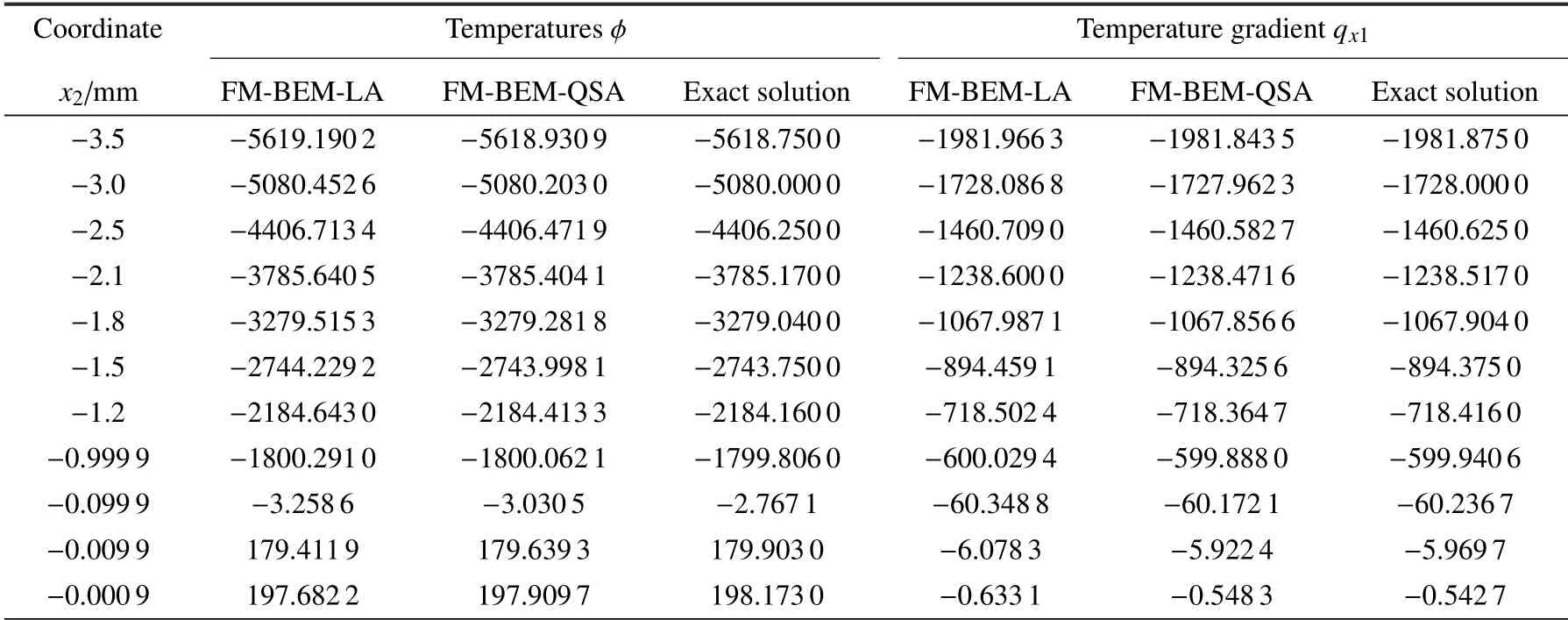
表3 正交各向异性不规则闭域D 点沿x1=10 附近的温度ϕ 和温度梯度qx1Table 3 Temperature and temperature gradient of inner point near point D(x1=10 mm)

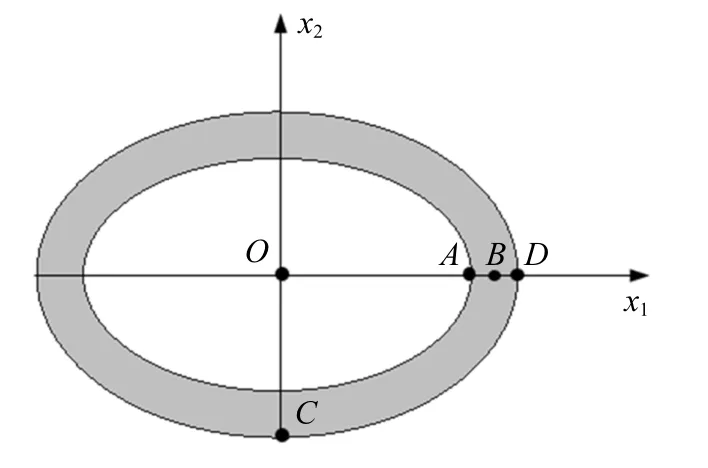
图8 椭圆环闭域热传导问题Fig.8 Heat conduction in the elliptic ring domain

定义厚长比δ=(b2−b1)/b1,δ 越小,结构越薄.使用FM-BEM 处理薄体问题时,近场积分的计算不仅仅涉及到奇异积分的计算,还涉及到几乎奇异积分的计算.当δ=0.02 时,正交各向异性椭圆环全域的温度云图和y1方向的温度梯度云图如图9 所示.表4 给出了取不同δ 的椭圆闭域结构中A,B,C,D点的温度ϕ 和温度梯度q的常规边界元法(CBEM)和FM-BEM 计算值,这里CBEM(二次元) 采用的是二次单元离散边界.与解析解相比,CBEM 和FM-BEM的计算结果在δ=1.0×10−1∼1.0×10−6范围内均保持高精度.当δ 减小至1.0×10−6时,FM-BEM-LA 计算结果失效,CBEM(二次元) 和FM-BEM-QSA 的计算结果依旧精确,与解析解的相对误差均小于0.1%.这是由于当δ 减小至1.0×10−6,若边界继续采用线性元离散,源点y落在了域外,其计算结果失效,而若边界采用二次元离散,源点y落在域内,其结果仍然精确,见图10.因此在离散超薄结构曲线型边界时,应采用二次元.对于超薄体结构,FM-BEM-QSA 的计算精度与二次元CBEM 几乎相同,在快速算法的帮助下,FM-BEM-QSA 能够处理大规模问题,具有更广阔的应用前景.

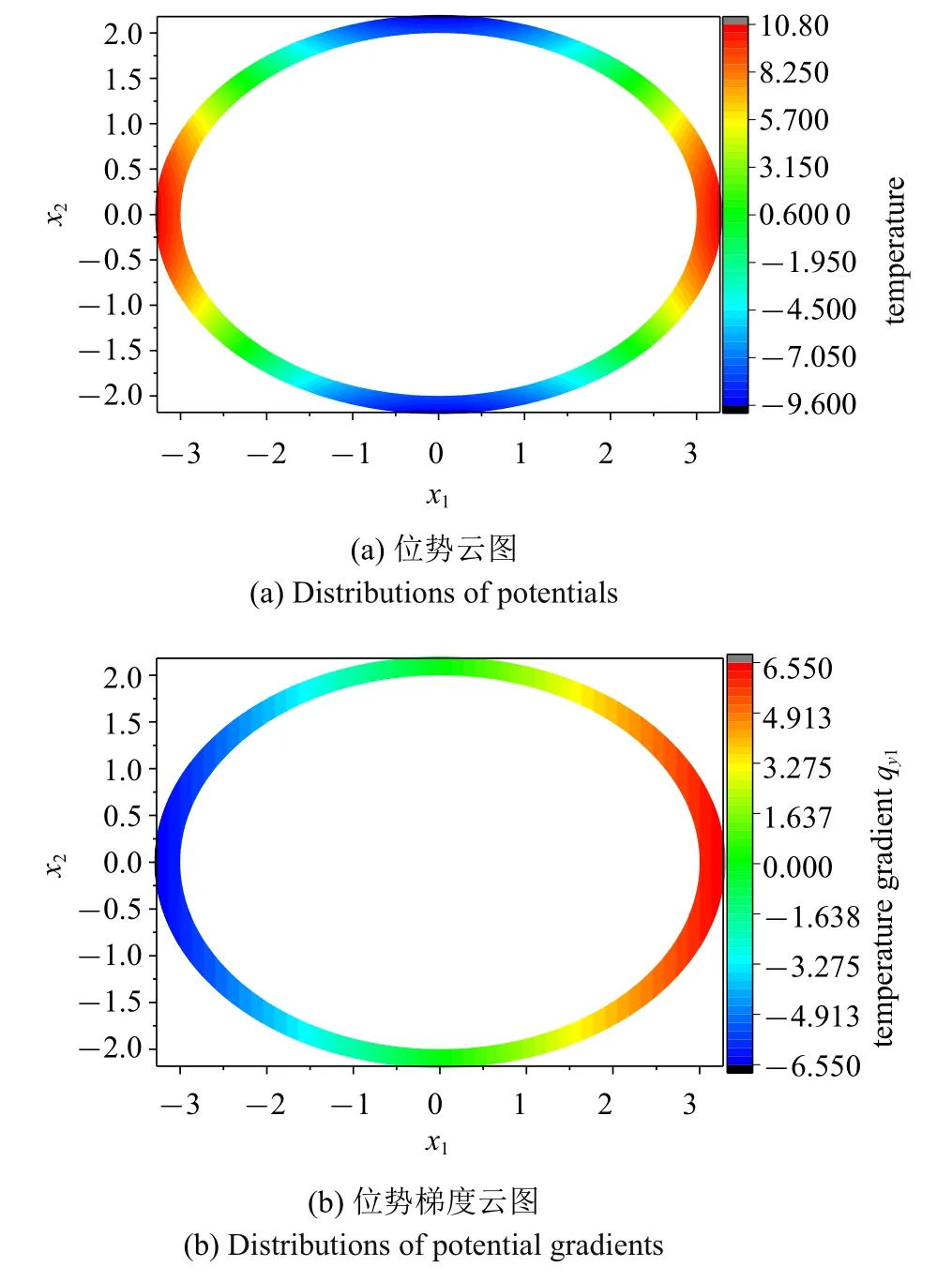
图9 正交各向异性椭圆环闭域全域的位势和位势梯度云图(δ=0.02)Fig.9 Distributions of potential and potential gradient of the orthotropic elliptic ring domain(δ=0.02)

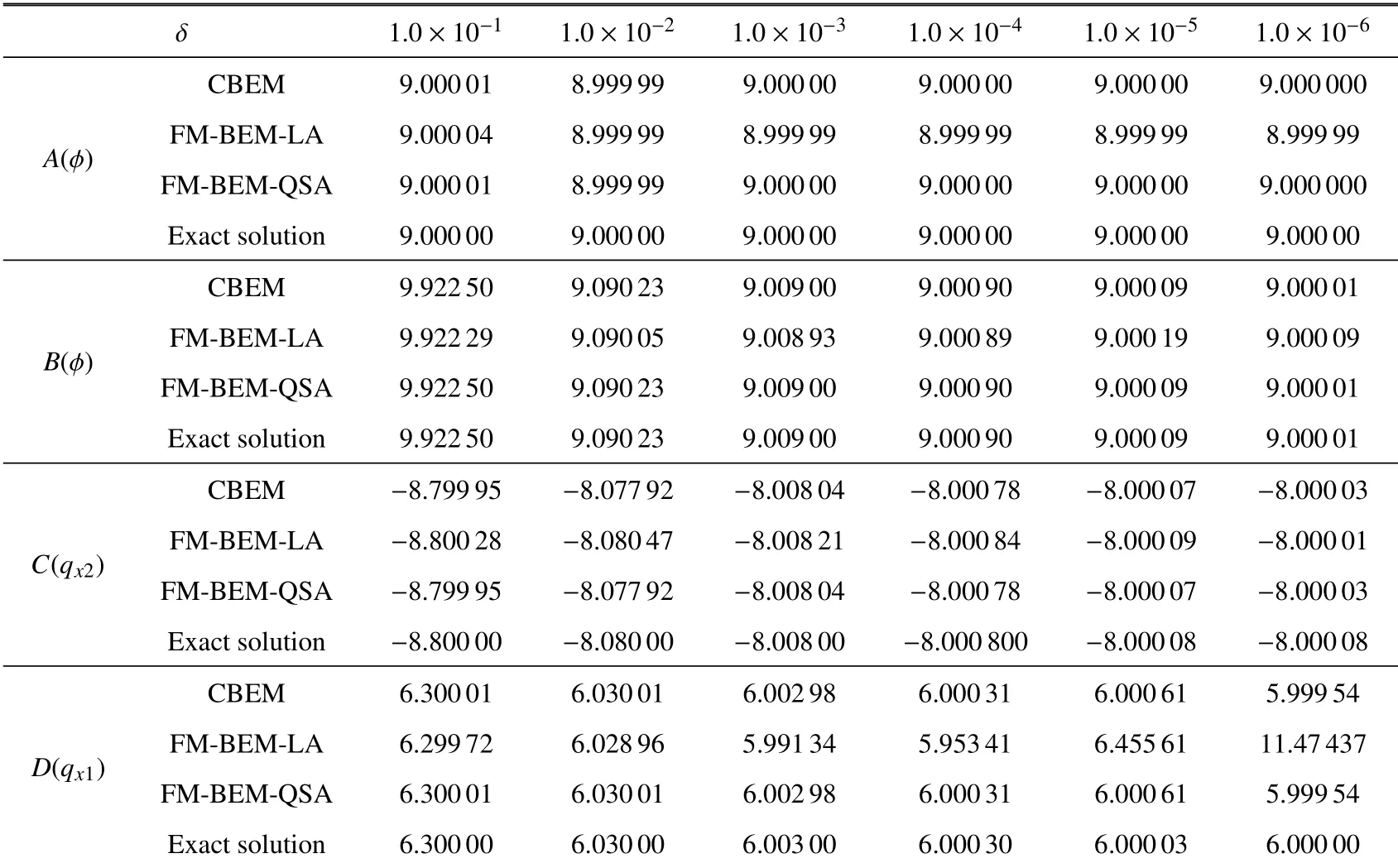
表4 正交各向异性椭圆环闭域A,B,C,D 点的温度ϕ 和温度梯度qTable 4 Temperature and temperature gradient of point A,B,C,D

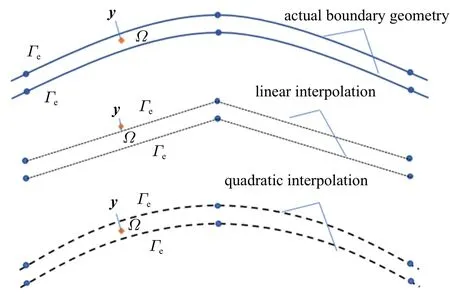
图10 源点y 相对单元几何说明Fig.10 Geometric relation between the source point y and element

3.3 随机多孔方板

考虑一个边长200×200 含多个随机孔的方板,如图11 所示,m×m个随机椭圆孔置于矩形方板中,其中m=100,200,300,400,500,600,800.传热系数ς1=1,ς2=2,每个椭圆孔边界采用360 个节点离散,方板的每条直边采用5000 个节点离散.矩形方板的左右两直边以及椭圆孔边的位势ϕ 已知,矩形方板的上下两直边的位势梯度q已知.该问题的解析解为ϕ=+3x1x2+5.所有的计算在一台Intel Xeon(R) CPU E5-2670 @2.60GHz 内存为16.0 GB 的电脑上完成.

采用FM-BEM 对随机多孔方板进行计算,通过调整随机椭圆孔的数量,获得采用FM-BEM-C,FMBEM-LA 和FM-BEM-QSA 消耗的CPU 时间与自由度(DOFs)之间的关系,如图12 所示.

图12 计算结果显示FM-BEM-C,FM-BEM-LA 和FM-BEM-QSA 所需CPU 时间与自由度数量成线性关系,计算量均处于O(N)量级.

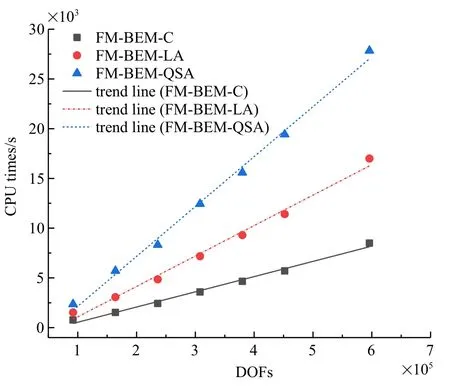
图12 CPU 时间与自由度的关系Fig.12 Relationship between CPU time and degrees of freedom

上述3 个算例的计算结果表明,在给定的计算精度下,相对于常值单元FM-BEM,高阶单元FM-BEM使用节点数显著减少,所需CPU 时间大幅度降低,因此高阶单元FM-BEM 可更加有效求解大规模问题.此外,高阶单元奇异积分和几乎奇异积分计算难题的解决,使得高阶单元FM-BEM 能够处理超薄体问题,拓宽了高阶单元FM-BEM 的适用范围.

4 结论

通过解决高阶单元奇异积分和几乎奇异积分的计算难题,建立了适用于二维正交各向异性位势问题的高阶单元快速多极边界元(FM-BEM),其优点如下:

(1) 高阶单元FM-BEM 的计算精度和计算效率较常值单元FM-BEM 的精度高.

(2)高阶单元奇异积分和几乎奇异积分难题的解决,使得高阶单元FM-BEM 能够应用于超薄体结构,具有广泛的应用前景.

(3) 高阶单元FM-BEM 计算时间与自由度数量成线性关系,其计算效率仍处于O(N) 量级,适用于求解大规模问题.