改进WOA的单液流锌镍电池充电策略
宋春宁,莫伟县,苏有平
(广西大学电气工程学院,广西 南宁 530004)
目前的电池充电优化技术,主要以缩短充电时间、降低能量损耗等目标为主[1],而影响的因素主要是充电电流。充电电流过大,虽然能缩短充电时间,但充电时的能耗也随之增大,反之亦然。孙志昆[2]设计了100阶段的充电策略,以充电时间与温升为优化目标,虽然能缩短充电时间、降低温升,但并未考虑环境温度的影响。陈亚爱等[3]为解决铅酸电池充电时的极化现象,提出一种基于马斯曲线的快速充电控制策略,用实验验证了提出的充电控制策略能实现快速充电,且不影响铅酸电池的使用寿命。单液流锌镍电池与双液流电池相比,只需要一个储液罐和一个电机,不需要昂贵的离子交换膜,具有循环寿命长、安全性能好、制造和维护成本较低、使用方便和无记忆效应等优点。研究该电池的充电过程,具有一定的意义。
鲸鱼优化算法(WOA)[4]是一种群体智能优化算法,在迭代计算过程中模仿座头鲸群体的捕食行为,来寻找目标问题的最优解。由于它的最优个体及运动方式依概率更新,具有更大的随机性和更快的收敛速度。黄清宝等[5]在WOA基础上提出了基于余弦控制因子和多项式变异的鲸鱼优化算法,有更快的收敛速度及收敛精度;O.Diego等[6]提出了一种混沌鲸鱼优化算法(CWOA),利用混沌变异增强算法跳出局部最优解的能力;王廷元等[7]提出一种基于自适应策略的混合鲸鱼优化算法,利用蝙蝠算法的局部搜索机制,达到增强种群多样性、避免过早陷入局部最优的目的,提高了收敛速度和寻优精度。
本文作者建立时间-能耗模型,并提出改进的WOA对电流值进行优化,实现对单液流锌镍电池的充电控制。
1 单液流锌镍电池时间-能耗模型的建立
1.1 单液流锌镍电池等效模型的建立
电池用的主流等效电路模型有电化学模型、内阻(Rint)模型、阻容(RC)模型、Thevenin模型和新一代汽车合作伙伴(PNGV)模型等。锌镍液流电池内部的化学反应复杂,采用电化学模型不利于分析与计算;内阻模型过于简单,只考虑一个电压源与一个内阻,不能很好地对锌镍液流电池内部反应进行描述;PNGV电路模型与RC模型,虽然能较好地描述锌镍液流电池内部反应,但存在计算复杂的问题。
综合模型精度和计算复杂程度考虑,选用Thevenin模型,为后面对电池的建模、辨识参数及SOC估算提供基础,模型如图1所示。
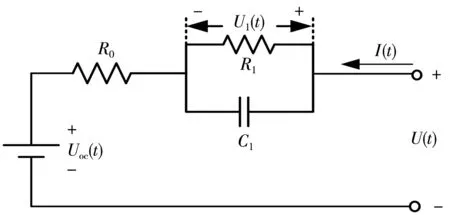
图1 电池的Thevenin模型
图1中:Uoc是开路电压(OCV);R0是欧姆内阻;R1、C1分别是极化电阻与极化电容;U是电池两端的电压;U1是极化电容两端的电压;I是充电电流值,箭头方向是电流方向;t是时刻。此外,模型还考虑了开路电压随SOC的变化[8]。
1.2 单液流锌镍电池等效模型的参数辨识
根据图1的电池Thevenin模型与基尔霍夫电压定律、基尔霍夫电流定律,得到辨识参数,满足关系式:
(1)
为了辨识电池的参数,可通过混合动力脉冲能力特性(HPPC)中脉冲充电曲线得到模型参数R0、R1与C1,单步脉冲充电曲线如图2所示。
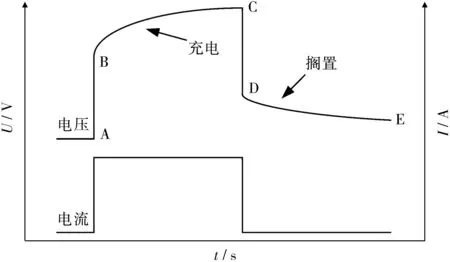
图2 单步脉冲充电曲线
在图2中,B点电压为UB、A点电压为UA;A-B阶段电压变化由欧姆内阻R0引起;B-C阶段电压变化由R1和C1组成的RC电路的零状态响应引起;C-D阶段电压变化是因为充电电流撤走的缘故;D-E阶段电压变化由R1和C1组成的RC电路的零输入响应引起;对应的零输入响应和零状态响应分别见式(2)与式(3),其中R1和C1组成的RC一阶电路的时间常数τ见式(4)。
U1=U1(0)e-t/τ
(2)
U1=IR1(1-e-t/τ)
(3)
τ=R1C1
(4)
式(2)-(3)中:e为自然常数。
根据图2所得,对应的欧姆内阻按式(5)计算。
(5)
在D-E阶段,根据式(2)通过MATLAB的cftool工具箱拟合计算,得到τ;在B-C阶段,根据式(3)及式(2)得到τ,然后拟合计算,求得极化电阻R1,再由式(4)得到极化电容C1,由此可得到电池不同SOC对应的R0、R1、C1及τ。参数可为后续建立时间-能耗模型提供数据基础。
实验用单液流锌镍电池的尺寸为40 cm×20 cm×60 cm,额定容量Cn为8.5 Ah,制备时的环境温度为 25 ℃,电解液的体积为2.0~3.0 L,其中氢氧化钾(张家口产,95%)浓度为10.00 mol/L,氧化锌(张家口产,99.5%)浓度为0.80 mol/L、氢氧化锂(张家口产,98%)浓度为0.25 mol/L;正极材料是氧化镍(智电芳华蓄电研究所提供)、负极材料是镀锌电极(智电芳华蓄电研究所提供)。用CT-3004-5V200A-NTFA电池综合测试柜(武汉产)进行测试。
1.3 单液流锌镍电池的SOC与OCV曲线
单液流锌镍电池的OCV与SOC具有函数关系,电池静置60 min后,极化电压U1衰减至接近0 V,此时端电压等于OCV。通过脉冲充电曲线可得到OCV与SOC的数据,再结合6次多项式拟合,得到式(6)的关系式:
Uoc=a0S6+b0S5+c0S4+d0S3+e0S2+f0S+g0
(6)
式(6)中:S是SOC,a0=-6.971、b0=23.74、c0=-32.06、d0=22.06、e0=-8.341、f0=1.833、g0=1.598。
1.4 时间-能耗模型建立
在建立时间-能耗模型前,将整个SOC(0~95%)每隔5%进行划分,分为N(N=19)个阶段,对应N个电流值对单液流锌镍电池进行分段恒流充电,电流为0.2~1.5C;选用最终SOC为95%是为了防止过充和排除上限电压的影响;选用间隔5%、分N个阶段,是因为充电的时间与电流大小有关,而产生的能耗与电流大小、欧姆内阻、极化内阻及极化电压有关。欧姆内阻、极化内阻及极化电压随SOC的变化而变化,通过间隔SOC进行分阶段充电,能更精准地描述产生的能耗;该模型输出的是充电产生的总能耗与总时间。
1.4.1 时间模型
分段恒流充电是每个阶段以不同电流对单液流锌镍电池进行充电,通过累加每个阶段的充电时间,得到单液流锌镍电池充电过程的时间模型,所对应的关系式见式(7)。
(7)
式(7)中:ttotal是整个充电过程的总时间;ΔQ是每个阶段充入的容量,即0.05×Cn;Ix是每个阶段的电流值。
1.4.2 能耗模型
对于所采用的Thevenin模型,能耗主要是由欧姆内阻R0及极化电阻R1产生,关系式见式(8)。
(8)
式(8)中:Eloss是充电过程中总能耗;Icharg是充电电流;R0与R1随着SOC变化而变化。
令Icharg[k]=Icharg[kΔt],U1[k]=U1[kΔt],假设kΔt到(k+1)*Δt时刻电流保持不变,则对式(8)进行离散化可得到式(9):
(9)
据式(9)所得,充电产生的能耗与分段电流值Icharg[k]、R0、R1和U1有关,而后三者与SOC有关,且随SOC动态变化,可以根据参数辨识得到对应的参数值。
2 SOC的估计与鲸鱼优化算法
2.1 扩展卡尔曼滤波(EKF)估计SOC
卡尔曼滤波算法是一种线性系统最优估计算法,最优值是由“预测值”+“修正”得到,但单液流锌镍电池是一个非线性系统对象,因此卡尔曼滤波不能直接用于该对象。扩展卡尔曼滤波(EKF)是在卡尔曼滤波的基础上,对非线性模型进行一阶Taylor级数展开,只考虑一次项,不考虑高次项,在非线性对象的展开点附近被近似线性化,从而使用卡尔曼滤波。
对于EKF的系统状态空间如式(10)所示:
(10)
式(10)中:x是状态向量;y是观测量;f、g都是非线性函数;w、v分别是过程噪声与测量噪声。
根据式(1),选取[S(k),U1(k)]T作为系统状态变量,端电压U作为输出量。基于Thevenin等效电路模型的一阶Taylor级数展开EKF离散状态空间方程,见式(11)。
(11)
式(11)中:ts是系统采样时间,一般ts=1 s;η是库仑效率,此处假定为1;Ik是充电电流。
2.2 鲸鱼优化算法
2.2.1 基本鲸鱼优化算法原理
鲸鱼优化算法是模仿座头鲸鱼气泡网攻击捕食行为的一种启发式优化算法,在群体捕食过程中,个体所处的坐标将作为问题的一个解,最优个体的位置即为最优解。该算法包括3个阶段:包围猎物、气泡网攻击和寻找猎物。
①在包围猎物阶段,数学模型如式(12):
X(iter+1)=X*(iter)-a(2r-1)|2rX*(iter)-X(iter)|
(12)
式(12)中:iter代表当前算法迭代次数;X、X*分别代表当前解和目前最佳解;r是[0,1]中的随机向量;权重a随着iter的增加,从2线性减小到0。
②在气泡网攻击阶段,数学模型如式(13):
X(iter+1)=|2rX*(iter)-X(iter)|eblcos(2πl)+X*(iter)
(13)
式(13)中:b为常数;l是[0,1]随机向量;π是圆周率。
③在寻找猎物阶段,数学模型如式(14):
X(iter+1)=Xrand(iter)-a(2r1-1)|2r2Xrand(iter)-X(iter)|
(14)
式(14)中:Xrand表示鲸鱼从种群中随机选择一个个体作为目标位置;r1,r2是[0,1]的随机数。
在WOA中,当控制参数A=|a(2r-1)|<1时,进行局部搜索,此时,鲸鱼以0.5的概率来包围猎物,以0.5的概率来进行螺线运动;当控制参数A>1时,算法进行全局探索。
2.2.2 一种改进的鲸鱼优化算法
权重a是线性减小的,即算法全局探索能力线性减小,局部搜索的能力线性增强。为增强算法的全局探索能力,避免算法过于早熟,黄清宝等[5]提出了一种改变参数a的方法(记为f1WOA),将a改为按照余弦曲线变化,使得a在算法迭代前期较大并缓慢减小,以充分进行全局探索,在算法迭代后期急速减小,以进行局部搜索。
在余弦曲线变化的基础上,本文作者提出一种改进的方式(记为f2WOA),增加了随机性,如式(15)所示。
(15)
式(15)中:itermax是最大迭代次数500;r3是[0,1]的随机数;k1、k2是[0,1]的数,且k1+k2=1。
当k1=0.3、k2=0.7时,权重a与迭代次数的关系如图3所示。
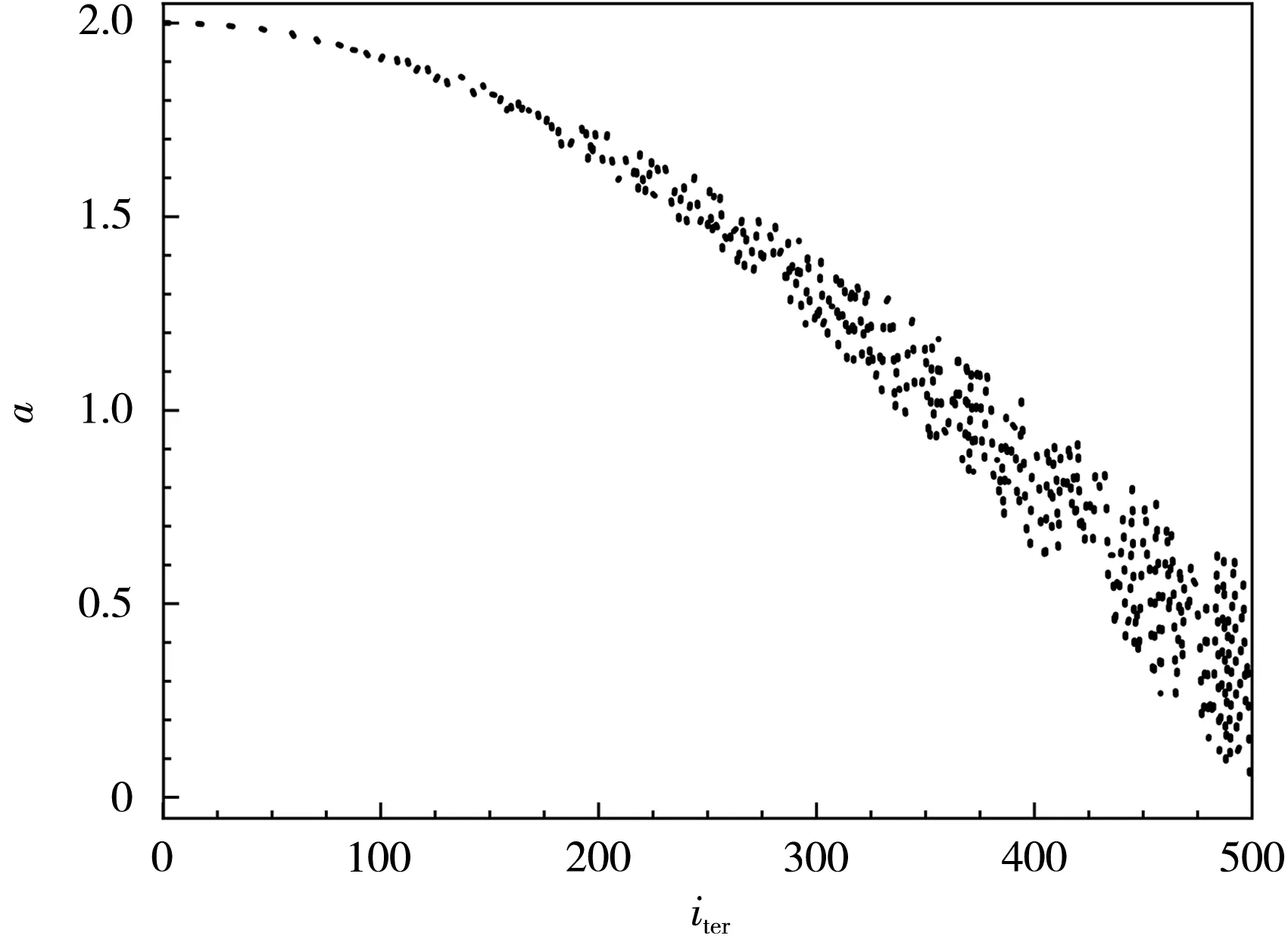
图3 权重a与迭代次数iter的函数关系曲线
从图3可知,在算法迭代后期,且此时适应度值的变化幅度比较小时,a能获得较大的权重,能增强算法的全局搜索能力,较好地跳出局部最优。
2.2.3 鲸鱼优化算法目标函数的建立
时间-能耗模型输出的是总时间ttotal、总能耗Eloss。当电流值大时,充电时间就短,充电过程能耗就高;电流值小时,充电时间就长,对应的能耗就低。这是两个相互矛盾的问题,因此对两个问题进行优化,是双目标优化问题。在双目标优化问题上,吴字强等[9]提出了一种针对燃料电池系统稳态输出功率与效率的优化算法,实现对输出功率和效率的最优化。对于双目标优化,常用的方法是权重系数变化法,实验用该方法将双目标优化问题转化为单目标优化问题[2]。
根据时间-能耗模型,优化0~95%SOC的电流值。在这个SOC范围内,对充电时间与充电过程的能耗进行整体优化,则单液流锌镍电池的目标函数如式(16):
Objective=αEloss+βttotal
(16)
式(16)中:α、β分别是能耗权重与时间权重,整个充电过程中,电流值不同,产生的能耗Eloss与充电时间ttotal也不同;Objective是时间能耗-模型的适应度。
因为Eloss、ttotal的单位不同,数量级也不相同,无法进行比较,并且会在后面计算适应度时产生偏差,无法得到准确结果,所以要对两个目标值进行归一化处理。常用的归一化方法有最大-最小标准化、Z-score标准化和函数转化等[10]。本文作者采用最大-最小标准化方法,但未将一个数值映射到[0,1],而是映射到[0,100]的区间,以便于比较。目标函数变换成式(17):
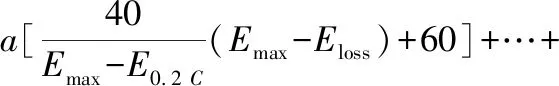
(17)
式(17)中:Emax、tmax是每个阶段电流取值最大(1.5C)时对应的充电产生的总能耗与充电所用总时间;E0.2 C、t0.2 C是每个阶段电流取值最小值(0.2C)时对应的充电产生的总能耗与充电所用总时间。Obj是目标函数变换后时间能耗-模型的适应度。
3 仿真与分析
3.1 改进的鲸鱼优化算法仿真分析
采用4个标准测试函数的shifted型进行仿真实验[5],分别为F1(shifted Sphere)、F2(shifted Quartic with noise)、F3(shifted Rosenbrock)和F4(Shifted Ackley),测试改进鲸鱼优化算法(f2WOA)的求解能力。所有仿真实验在PC上运行,程序为Matlab 2014a的M脚本语言。测试函数见表1。

表1 4个标准的偏移型测试函数
表1中:xi是函数解x的第i维量的值;oi是偏移量o的第i维量的值;zi是过程变量。
将改进的鲸鱼算法(f2WOA)与基本的鲸鱼优化算法(WOA)、余弦变化的鲸鱼算法(f1WOA)进行比较。实验设置为:种群规模N=50,最大迭代次数为50 000次,偏移量oi(i=1,2,……,n)为搜索范围内的随机值。3种算法分别对每个测试函数独立运行30次,记录算法求得的最优函数值的平均值(Ave)和标准差(Std),其中平均值反映了算法的求解精度,标准差反映了算法的求解稳定性,运算结果见表2。

表2 测试函数优化结果对比
从表2可知,在求解精度及稳定性方面,改进的鲸鱼优化算法(f2WOA)要优于WOA与f1WOA。
3.2 算法(f2WOA)求解时间-能耗模型仿真分析
为了验证该方法(f2WOA)能否达到优化目的,采用文献[11]中恒流恒压方法中的0.5C恒流充电方式进行实验对比。实验选择的SOC是0~95%,即当SOC等于95%为充满,电流值取值为1.70~12.75 A(0.2~1.5C)。选用改进的鲸鱼优化算法(f2WOA)求得能耗权重α与时间权重β比重不同时,充电过程产生的能耗与所用时间,以及0.5C恒流充电产生的能耗与所用时间,结果见表3。
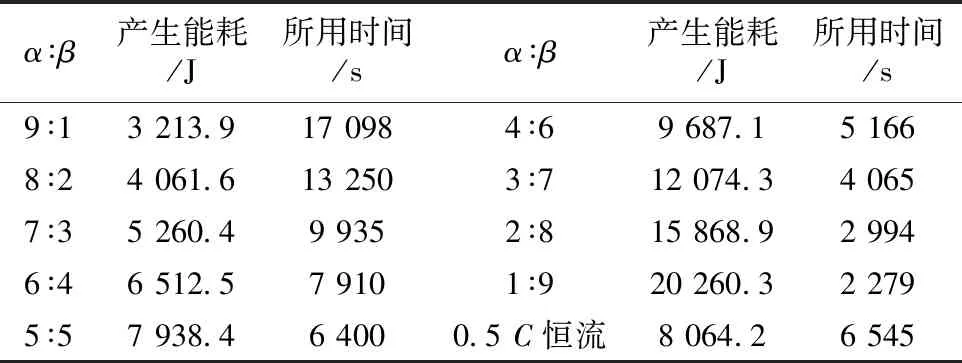
表3 不同α、β比及恒流充电产生的能耗与所用时间
从表3可知,当α∶β为9∶1~6∶4时,充电产生的能耗较少,但充电时间延长;当α∶β为4∶6~1∶9时,充电所用的时间缩短,但能耗增加。
将表3数据作图,得到图4,不同α、β比优化后的电流值列于表4。
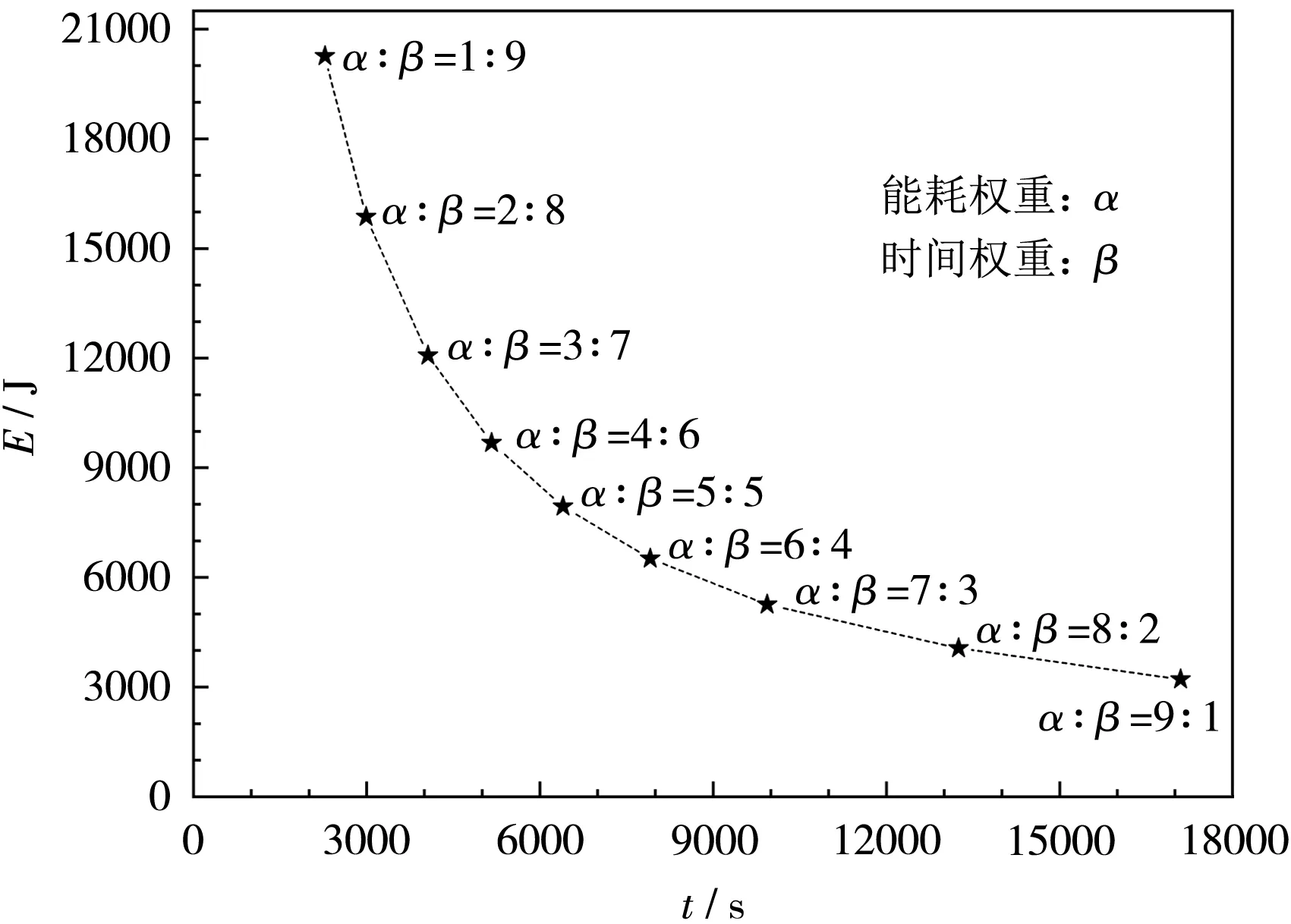
图4 不同权重比优化结果
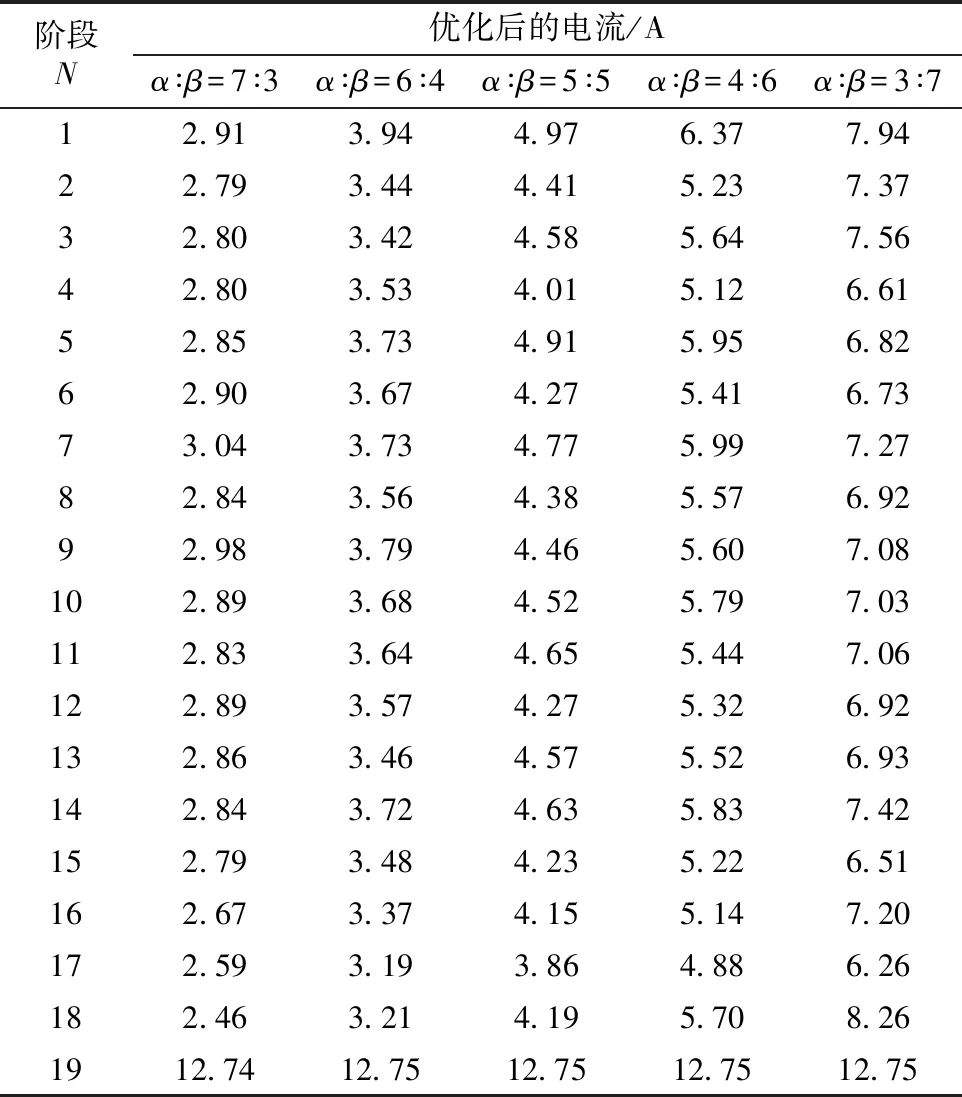
表4 不同α、β比优化后的电流值
从图4可知,当能耗权重α占比较大时,优化偏重于能耗,所对应产生的能耗较短,但充电所用时间较长;当时间权重β占比较大时,优化偏重于时间,充电所用时间较短,但产生的能耗较多。这是两个相互矛盾的指标,要根据不同侧重点选用不同的能耗权重α、时间权重β比。
当α∶β=5∶5时,能耗较恒流充电少了125.8 J、时间缩短了145 s,即能耗减少了1.58%、充电时间缩短了2.27%。结果表明,通过SOC来进行分阶段充电,以产生能耗和充电所用时间为目标进行优化,可以降低能耗及缩短充电时间。
4 结论
本文作者提出了改进的鲸鱼优化算法(f2WOA),在求解复杂问题上与余弦变化的鲸鱼算法(f1WOA)、基本的鲸鱼优化算法(WOA)相比,有较优的求解精度及稳定性。通过脉冲充电实验,辨识得到电池的具体参数,建立时间-能耗模型,使用改进的鲸鱼优化算法(f2WOA)优化该模型。仿真分析结果表明:通过分阶段对单液流锌镍电池进行充电,采用优化后的电流值,较0.5C恒流充电能耗减少1.58%、充电时间缩短2.27 %。本文研究过程中,假定电池的参数不变,没有考虑到电池受到老化及电解液流速的影响,在后续的研究中可考虑添加这两方面的内容。

