活性粉末混凝土梁抗剪承载力分析

罗 华,骆雅洁,尹萱洋,周 亮,刘王苗

(1.湖南理工学院 土木建筑工程学院,湖南 岳阳 414006;2.湖南理工学院 南湖学院,湖南 岳阳 414006)

0 引言

活性粉末混凝土(Reactive Powder Concrete,RPC)是一种具有广阔应用前景的高性能新材料.以往的研究大部分集中在材料的性能方面[1～5],近年来对RPC构件的抗弯承载力和变形性能研究较多[6～9],对RPC梁的抗剪性能研究较少.作为一种具有较高抗压、抗拉强度的混凝土,RPC的抗剪性能对其在工程中的应用至关重要.邓宗才[10]等基于修正压力场理论,提出了配筋RPC梁抗剪承载力计算方法.王强[11,12]等基于修正压力场理论及塑性理论分别推导了RPC梁的受剪承载力简化计算公式.罗伯光[13]等采用桁架拱模型推导了RPC梁抗剪承载力计算公式.因此进行RPC梁抗剪性能的研究,为RPC构件的设计提供相应的理论基础具有重要意义.本文基于软化桁架理论,提出RPC梁抗剪承载力的一种计算方法.

1 RPC梁抗剪承载力计算模型

1.1 软化桁架理论计算模型

软化桁架计算模型如图1所示.配筋RPC梁在荷载作用下,剪跨区将出现斜向裂缝,从而形成桁架.

软化桁架理论应用于配筋RPC梁抗剪分析基于以下假定:(1)弯矩由桁架的弦杆承受;(2)混凝土的主应力方向与主应变方向一致,且与纵筋成α倾角;(3)腹板上的剪应力平均分布;(4)只考虑RPC和钢筋的总体行为,RPC开裂后仍假定RPC与钢筋之间的应变协调.

1.2 剪跨区内微元体的应力求解方程

(1) 剪应力τlt

对于T形截面,考虑上翼缘板部分参加抗剪,如图2所示.根据假定,剪应力在正截面腹板上平均分布,于是

其中b为腹板的厚度;h0为腹板的有效高度;c为上翼缘Ap参加抗剪对腹板厚度的增大系数.

图1 软化桁架计算模型

图2 T形截面受力

(2) 竖向正应力σt

竖向正应力σt可由与剪应力τlt的比例常数k决定:

其中k由所选计算截面位置和剪跨比计算确定.

(3) 纵向正应力σl

以往研究表明,钢筋混凝土梁小剪跨比(一般λ＜2)情况下,截面所受弯矩相对较小,可忽略,即假定

但在大剪跨比(λ≥2)情况下,弯矩的影响不可忽视.考虑剪跨比的影响,按平截面假定腹板的平均纵向应变为

其中εa为桁架上弦杆的应变;εb为桁架下弦杆的应变.

为确定上下弦杆的应变,首先根据桁架中受力平衡条件计算桁架中弦杆的内力,再由求得的上下弦杆的内力计算出上下弦杆应变:

其中Aa,Ab分别为上弦杆混凝土、下弦杆钢筋的截面面积;Ec,Es为材料相应的弹性模量.

2 基于软化桁架理论的计算结果与已有文献试验结果比较

基于软化桁架理论进行RPC梁斜截面抗剪承载力全过程分析,并采用MATLAB软件编程计算文[14]中试验梁的抗剪承载力.理论计算值与试验实测值比较见表1.

图3、图4分别为开裂荷载理论计算值与试验值比较结果和极限荷载理论计算值与试验值比较结果.由图3可以看出,由理论计算所得开裂荷载与试验结果符合较好,其中理论值与试验值比值的平均值为1.037,标准差为0.131.由图4可知,由理论计算所得极限荷载与试验结果符合也较好,但由于试验梁L-1-100-a、L-1-100-a-8及l-1-100-a剪跨比较小,承载力很高,试验难以测得极限荷载.不计这三根试验梁的结果,极限荷载理论值与试验值比值的平均值为0.9797,标准差为0.0406.

表1 计算开裂荷载和极限荷载与文[14]试验结果比较

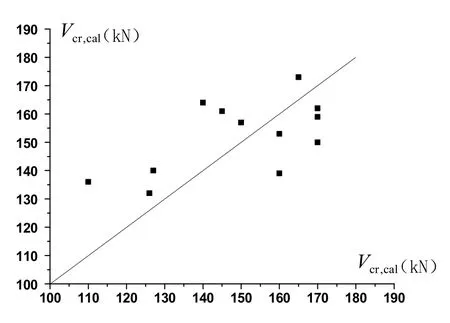
图3 开裂荷载理论计算值与试验值比较

图4 极限荷载理论计算值与试验值比较

3 计算结果与其他试验结果比较

为验证本文计算模型的适用性,对文[13,15]中的RPC梁抗剪承载力进行了计算,并与原文中的试验结果进行了对比.理论公式计算结果与文献试验结果比较见表2.

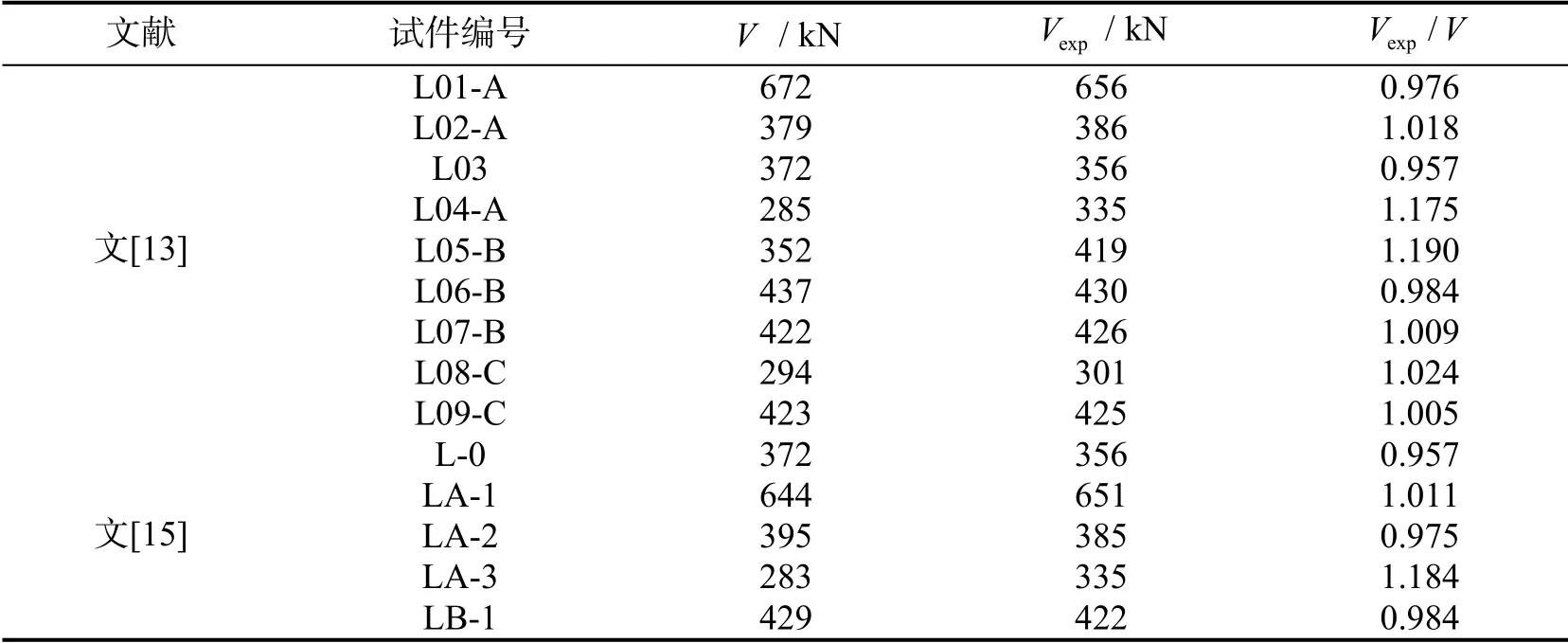
表2 计算结果与文献试验结果比较

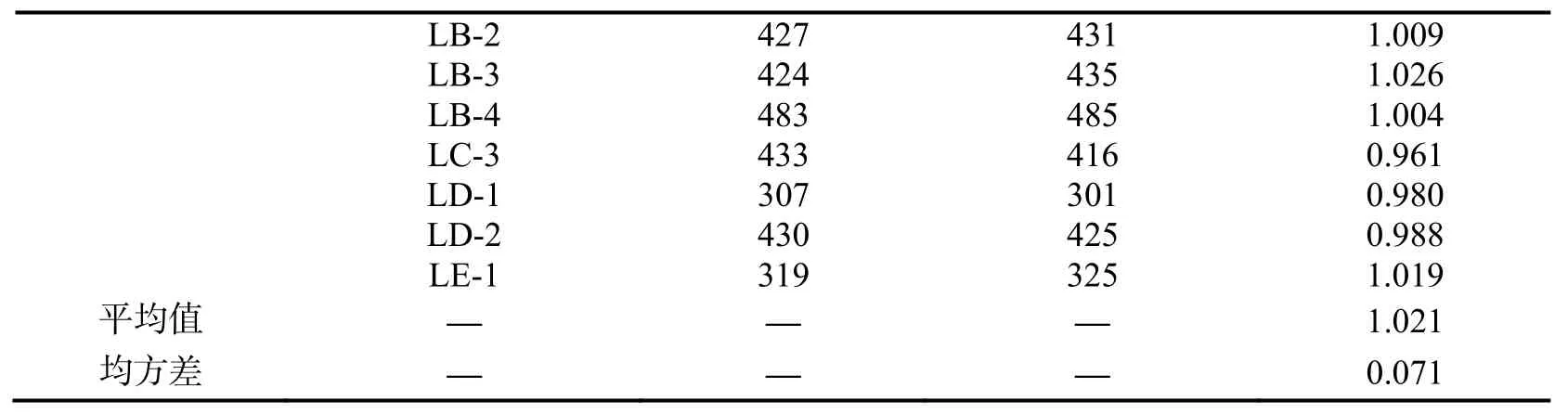
注:V为公式计算值,Vexp为试验数据.

由表2中数据比较可知:试验值与理论值之比的平均值为1.021,均方差为0.071,试验值与理论值较吻合,离散系数较小.这说明,本文提出的抗剪承载力计算模型可应用于RPC梁抗剪设计与计算.

4 结论

(1) 基于软化桁架理论的受剪破坏分析,可以较好地模拟活性粉末混凝土梁的抗剪性能,且抗剪承载力的计算结果与试验结果吻合较好.

(2) 将本文的计算模型应用于文[13～15]中RPC梁抗剪性能试验,计算结果与试验结果吻合较好.因此,采用本文计算模型来预测RPC梁的抗剪承载能力是可行的.