基于三维重建飞机气动特性的飞行包线
苏光旭, 张登成, 张久星
(1.空军工程大学航空工程学院, 西安, 710038; 2.94916部队, 南京, 211500; 3.93756部队, 天津, 300131)
飞行包线是以飞行速度、飞行高度、载荷等为边界用来表示飞机飞行范围的封闭图形[1],是飞机飞行性能关键指标。飞行包线是确保飞行安全的基础,现代战斗机通过多种包线限制可以实现飞行员的“无忧虑”飞行。文献[2]按照飞行任务将飞行包线分为基本飞行包线、小表速包线、大表速包线、发动机空中启动包线、速度载荷包线、突发载荷包线以及安全弹射救生包线等。基本飞行包线是以飞机平飞状态下的失速限制、理论升限,以及最大平飞速度限制所组成的飞机飞行边界。
对于飞行包线的计算与应用,国内外学者做了大量研究。文献[3]提出了多种评估军用飞机飞行边界的方法,可以通过评估未知飞机的飞行性能进而给出飞行边界。文献[4]和[5]基于飞行数据,通过可达平衡集的评价方法求取飞机所有状态点的机动能力,给出了飞机的机动飞行包线。文献[6]基于飞机的包线数据库,提出了一种针对机翼故障的估算动态飞行包线以确保飞行安全的方法。文献[7]使用现有的飞机几何模型计算了飞机结冰数据库,提出了一种基于神经网络自适应动态逆的结冰飞机飞行安全边界保护方法。综合现有研究成果,飞机的气动特性是飞行包线计算的关键,而几何模型是气动特性计算的基础,很少有针对气动参数未知的飞机建立精确飞行包线的工作先例。
综上所述,本文是以气动参数未知飞机的飞行安全和空战仿真为研究背景,对飞机几何模型进行三维重建,应用计算流体力学(computational fluid dynamics, CFD)分析了飞机的纵向气动特性,基于所计算的气动数据通过“简单推力法”[8]确定平飞包线,增加最大平飞速度限制条件,给出了飞机的基本飞行包线。气动特性分析与包线计算充实了该飞机的飞行性能,为飞机的飞行安全提供了技术支撑,为其动作库构建和空战仿真奠定了基础。本文的研究方法,是一个完整的从飞机逆向建模到飞行包线计算的技术途径。
1 飞机几何外形三维重建
某几何外形参数未知的飞机是一种翼身融合的常规气动布局双发重型战斗机,本文综合运用图像明暗恢复形状和工程图重建法建立飞机的三维几何模型,为数值模拟计算进行模型准备。其主要步骤介绍如下:
1)透视参数求解。由图形学知识,通过照相机标定可以求解图像的透视参数,包括相机焦距、视点距离、坐标系转换矩阵等。如图1所示,对于飞机照片一般使用“仅知两个灭点的相机标点”[9]方法,通过优化迭代计算第三灭点的位置,从而求解各透视参数。
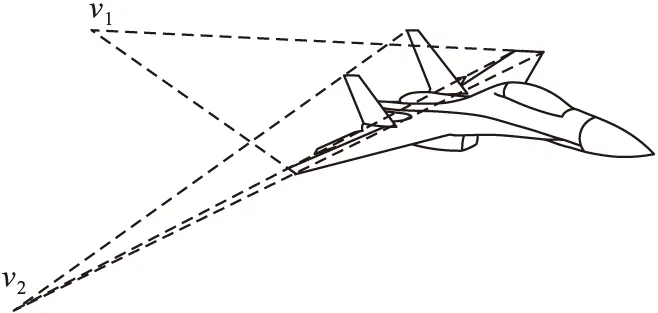
图1 飞机照片的两个灭点
2)图像明暗恢复形状建立局部三维曲面。使用图像明暗(灰度)恢复形状(shape from shading,SFS)可以初步求解观察体曲面的初始高度值[10-11]。在已知反射特性的前提下,依据图像灰度约束方程[12]求解模型的表面梯度,得到物体的表面高度,即可恢复曲面的外形。本文使用三次参数样条曲线拟合[13]曲面的高度数据构建局部三维外形,如图2飞机机头锥的线框模型。

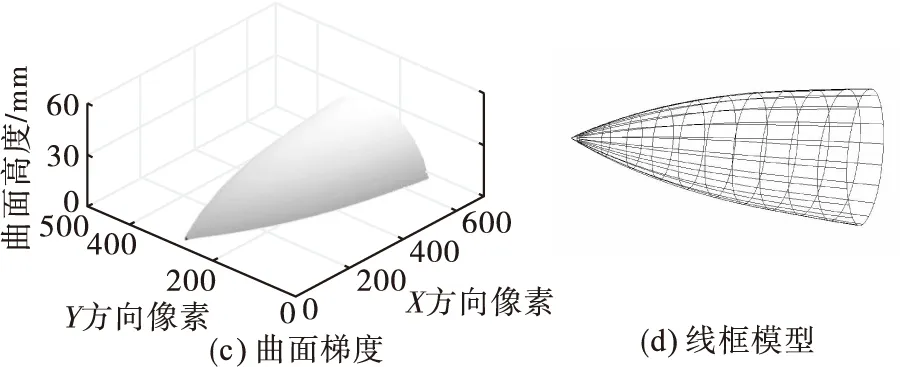
图2 飞机机头锥的重建过程
3)工程图重建法整合飞机整机模型。飞机整机模型的三维重建是一个复杂繁琐的过程,需要分成不同部件和曲面进行重建,本文根据平行投影原理通过工程图重建法[14]进行整机模型的拼接。另外,对于气动参数影响较大的部件如机翼等,需要使用翼型数据辅助建模。图3给出了整合后飞机的线框模型以及模型的渲染效果。

图3 整机线框模型与渲染效果
2 气动特性计算
使用重建的飞机三维几何模型,在不同巡航高度、迎角和马赫数的飞行状态下进行数值模拟计算,得到气动数据并分析其纵向气动特性。
2.1 网格划分与计算条件
使用成熟的CFD计算软件进行数值模拟计算。网格划分(图4)为非结构网格,网格总数922万。边界层内第1层网格高度控制在0.002 mm,以满足机体表面黏性边界层的计算要求[15]。
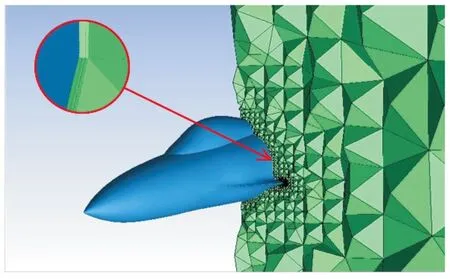
图4 网格划分
求解计算条件中,飞机表面使用无滑移壁面条件,外场壁面定义为压力远场条件,湍流模型使用对涡黏性系数修正的方法以适应不同区域流动的Spalart-Allmars模型。
2.2 网格无关性与算例验证
为了进行网格无关性验证,在Ma=0.8、α=5°、飞行高度h=10 km工况下,选用3套非结构网格计算整机的升力系数和阻力系数。网格数和计算结果见表1,网格划分情况见图5。通过对比可见网格量变化对计算结果影响微弱,为了兼顾计算精度和计算时间,选取中网格。

表1 不同网格量升力系数和阻力系数计算结果对比
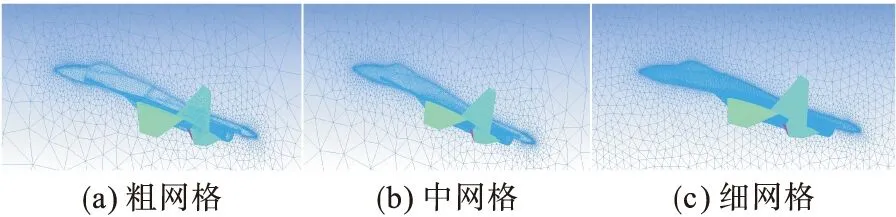
图5 不同网格量的网格划分
采用AIAA阻力会议的标模DLR-F6翼身组合体作为验证模型[16]来检验本文计算方法的正确性。选用相同的S-A湍流模型和计算条件,该翼身组合体网格划分和计算结果如图6所示,分别计算了机体的升力系数CL、阻力系数CD、机身俯仰力矩Cm,其中Exp为试验数据,S-A为数值计算结果。可以看出,仿真计算结果与试验数据吻合较好,满足工程应用的要求。

图6 模型算例验证
2.3 气动特性分析
在软件计算精度验证的基础上,对图3所示飞机模型计算不同飞行高度,飞机从亚声速到超声速不同迎角下的纵向气动特性,下面以飞行高度h=10 km为例进行分析(见图7)。

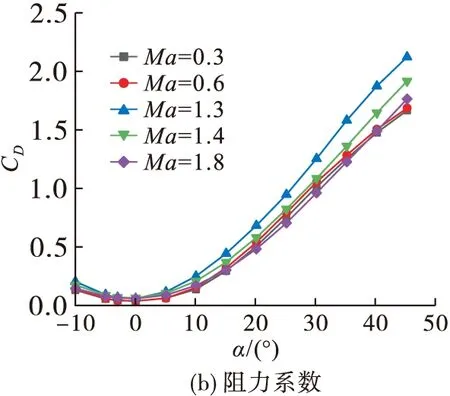
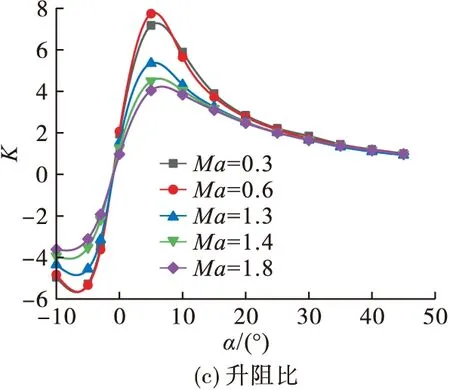
图7 h=10 km纵向气动特性
图7给出飞机的升力系数CL、阻力系数CD和升阻比K(K=CL/CD)随迎角α的变化拟合曲线。从不同飞行马赫数下升力系数随迎角变化规律可以看出,升力系数随着迎角增大成S型增长,零升迎角在-2°左右,失速迎角在30°左右,说明该飞机的气动布局具有较好的大迎角失速特性。就不同的飞行马赫数来看,飞机在跨声速飞行时升力系数变化率最大,而低马赫数飞行时飞机的升力系数变化率最小。
从阻力系数随迎角的变化规律可以看出,在小迎角飞行(α<10°)状态下,阻力系数随迎角增大增长的较为缓慢,而在较大迎角飞行状态阻力系数随迎角增大呈线性增长。就不同的飞行马赫数来看,随着飞机飞行马赫数增大,整机的阻力系数先增大后减小,在Ma=1时阻力系数达到最大值,且增长率最大。
从升阻比随迎角的变化规律可以看出,随着迎角增大,升阻比呈现出先减小后增大再减小的趋势,最大升阻比的峰值均在α=5°左右,而且马赫数越小这种变化越明显。最大升阻比7.726出现在Ma=0.6时,随飞行马赫数增大,最大升阻比逐渐减小,Ma=1.8时最大升阻比减小为4.04,说明飞机在小迎角亚声速飞行状态下具有较好的亚声速巡航特性。
根据升力特性可知飞机具有较好的大迎角失速特性,为了分析其大迎角状态下的流动机理,图8给出了Ma=0.8时不同迎角下飞机纵向的涡强分布。可以看出,来流经过边条翼时形成了明显的脱体涡,这个最明显的脱体涡的尺度表示了流经机翼上方湍流的宏观尺寸,脱体涡的形状不规则,大体环绕在机翼上方,沿机身纵轴尺度不断增大。通过对比可以发现,随着迎角不断增大,脱体涡强度不断增大,涡流动速度加快,加强了切洗效应[17],机翼的低压区和低压程度不断增大,这是升力增大的主要原因。当迎角为30°时,机翼上方脱体涡的尺度扩大,出现了破裂的趋势,切洗效应减弱,此时的升力系数接近峰值,当迎角再增大时,对应图7(a)升力系数变化规律,升力系数开始减小。

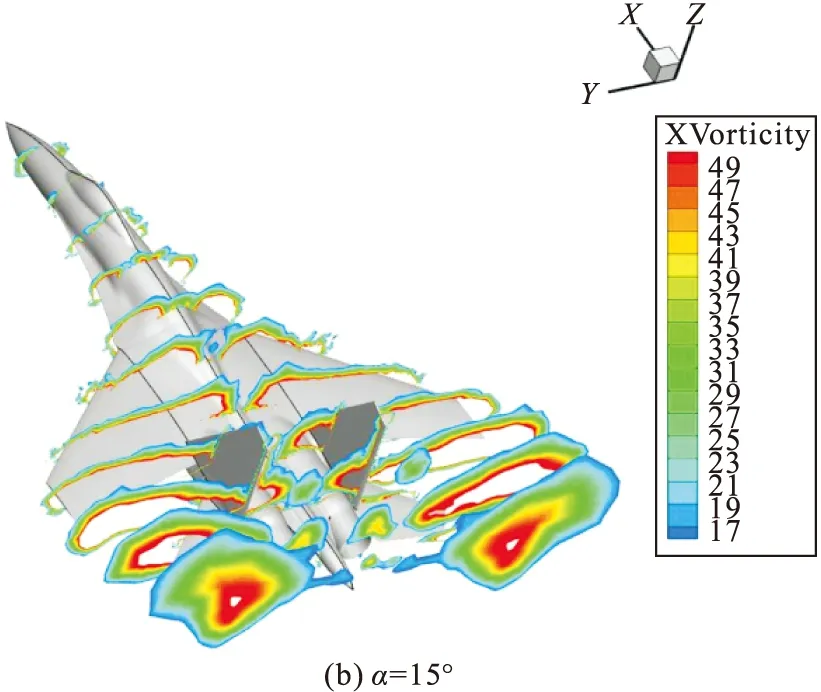
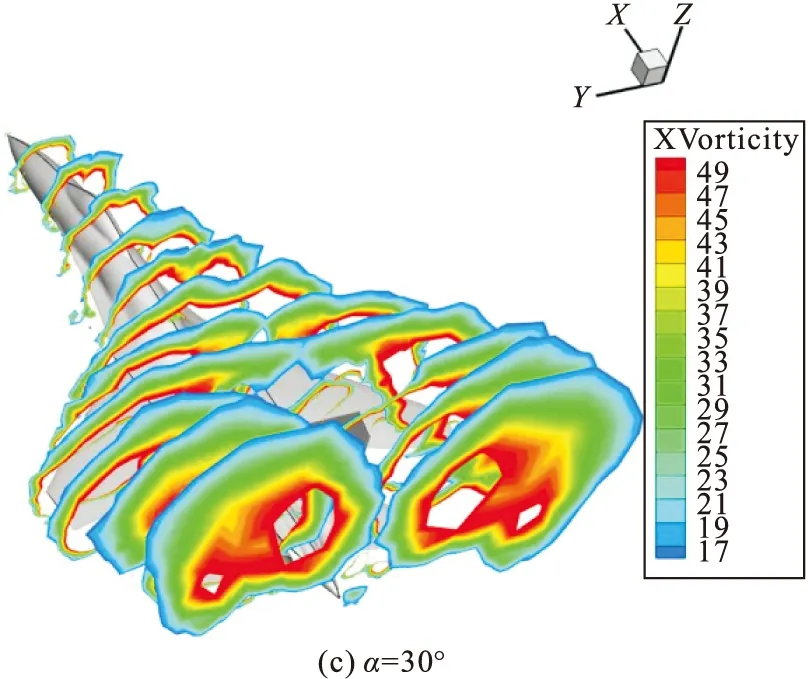
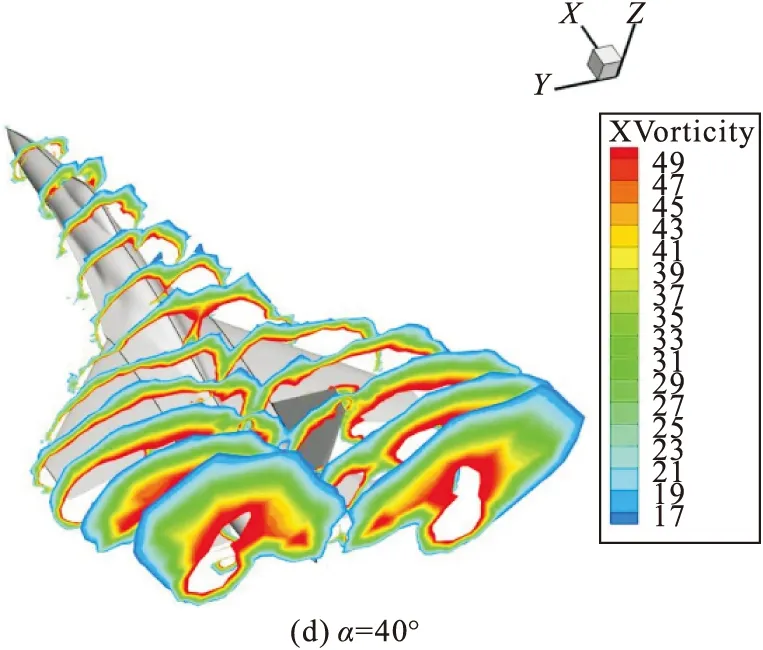
图8 0.8 Ma时不同迎角涡强分布
3 飞行包线的计算
基于CFD计算的气动参数,使用“简单推力法”加平飞最大速度限制条件的方法分别求解飞机的最小平飞速度、静升限以及最大平飞速度,给出飞机的基本飞行包线。
3.1 最小平飞速度
最小平飞速度是飞机在某一高度下能够保持平飞的最小速度,是基本飞行包线的左边界,即失速限制。根据平飞条件,求某一固定高度下的最小平飞速度,需联立以下公式:
(1)
CL max=fMa
(2)
式中:CL max为飞机最大允许升力系数;v′为当地声速;ρ为空气密度,取决于飞行高度h;S为机翼面积。式(1)为飞机的平飞约束条件,即升力与重力相等。式(2)体现了飞机的气动特性,可以根据CFD计算结果进行拟合得到。
选取一系列适当的Mai(i=1,2,…),根据平飞约束条件式(3)可解得选取马赫数Mai所对应的最大升力系数CL max i,求CL max i~Mai拟合曲线与CFD计算结果拟合曲线的交点,可以得到在某一高度下的平飞最小速度,即Mamin=0.342。
(3)
图9给出了h=10 km时2条曲线的拟合结果,图中Polyfit表示多项式拟合结果,下同。
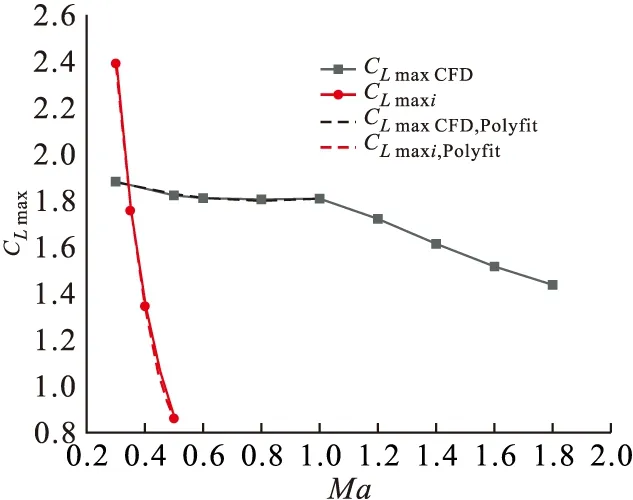
图9 h=1 km CL max随Ma变化关系
求得不同高度的平飞最小速度之后进行拟合即得飞行包线左边界,见图10。

图10 不同高度下的最小飞行马赫数
3.2 升限的确定
飞机的静升限,又称为理论升限,定义为飞机的最大上升率为0时的飞行高度,即所能保持平飞的最大高度。飞机上升率为飞行速度在竖直方向上的速度分量,根据定义有:
(4)
式中:θ为飞机的航迹俯仰角。
当飞机在铅锤面内作定常运动时,假设飞机的迎角α不大且飞机的推重比较小,则飞机在铅锤面内的质心动力学方程可以表述为:
(5)
式中:PAVL为发动机的可用推力;L为升力;D为飞行阻力。另根据平飞的限制条件,其所需推力Pr等于飞行阻力,经推导可得:
(6)
所以,当飞机的最大上升率为0时,有:
(7)
因此,计算固定马赫数下飞机平飞时的升阻比K,当在某一飞行高度下K满足上式时就可以得到对应飞行马赫数下的理论升限。
下面以Ma=1.2为例说明计算过程:
1)根据飞机平飞的限制条件,求解当Ma=1.2时不同飞行高度下平飞所需升力系数CL,L=G,如表2所示。

表2 Ma=1.2不同高度下的平飞升力系数
2)根据CFD计算结果,将不同飞行高度下飞机升阻比K随升力系数的变化规律进行多项式拟合,如图11所示。根据拟合结果求解不同飞行高度下平飞所需升力系数对应的平飞升阻比KL=G,如表3所示。
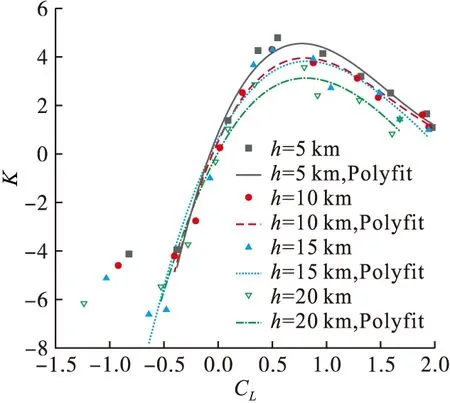
图11 不同高度下升阻比随升力系数的变化

表3 Ma=1.2不同高度下的平飞升阻比
3)根据2)的计算结果,得出G/KL=G随飞行高度的变化规律并进行拟合,见图12。其实,这里的G/KL=G即为Ma=1.2时飞机的平飞所需推力Pr随飞行高度的变化关系,将平飞所需推力与可用推力绘制在同一曲线图上,曲线的右交点所对应的飞行高度即为飞机在Ma=1.2时的理论升限hmax=16 077 m。
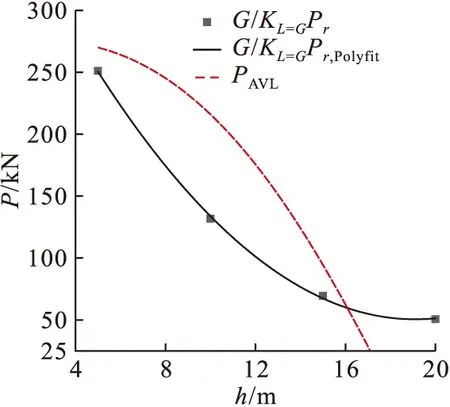
图12 可用推力与平飞所需推力变化
分别计算不同飞行马赫数下的理论升限,即可得到飞行包线的上边界,如图13所示。
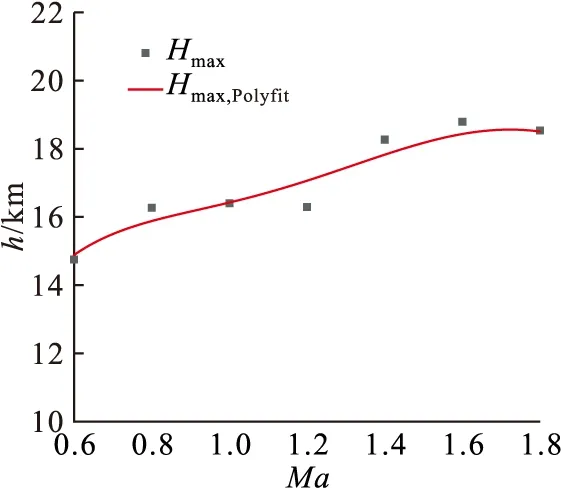
图13 理论升限随马赫数的变化关系
3.3 最大平飞速度
根据平飞条件,由PAVL=Pr可以得到由推力限制的最大平飞速度,但是现代高性能战斗机由于气动外形的改进和发动机推力的提升,按照简单推力法计算得到最大平飞速度一般会超过飞机所能承受的结构强度、刚度和温度极限,因此,本文综合运用动压限制、温度限制和推力限制的方法确定飞机的最大平飞速度。
3.3.1 动压的限制
具有超声速飞行能力的飞机在飞行高度h≤12 km时最大平飞速度主要受到所能承受的最大气动载荷,即动压的限制[3]。动压限制通常以最大允许表速的形式对飞行员显示,它体现了飞机机体结构的刚度和强度。文献[18]提出了一种使用气动弹性静力学模型求解飞机最大气动载荷的方法,较为繁琐,本文结合与该飞机具有相似构造的同类飞机A以及外军具有类似战术指标飞机的飞行性能[19]估算该型飞机的最大允许表速。
飞机在海平面飞行时最大允许表速等于给定最大气动载荷的飞行真速,根据换算关系可以计算出最大允许表速在不同飞行高度所对应的飞行马赫数,如图14的动压限制所示。
3.3.2 温度的限制
飞机在高速飞行时,气动增温使机体表面温度急剧升高,当温度过高时机体结构材料会产生机械性破坏,因此机体表面的温度也限制了飞机的最大平飞速度。现代军用飞机蒙皮所使用的材料主要有铝、镁合金,在一些特殊部位会使用少量的钛合金或者以碳纤维为代表的高性能复合材料[20],其中能够承受温度最低的是铝合金类材料,以此作为机体表面温度的限制值是合理的。
根据空气动力学知识,气动增温主要取决于环境温度Ti和Ma,有:
T0=Ti(1+0.2Ma)2
(8)
式中:T0为机体表面温度;Ti取决于飞行高度。因此,可以通过最大温度限制计算出不同飞行高度下的Mamax,温度限制如图14所示。
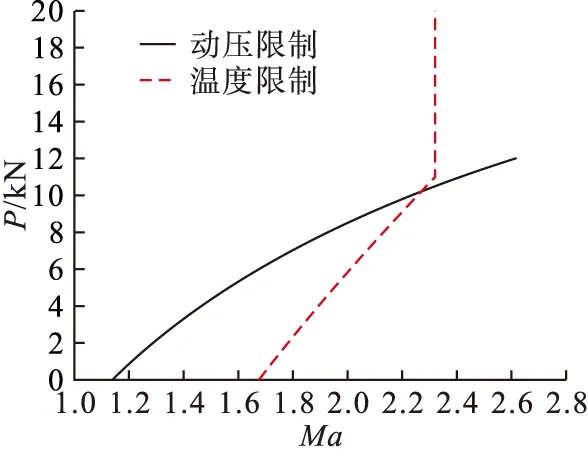
图14 动压和温度限制的最大平飞速度
3.3.3 推力限制
推力的最大值也限制了最大平飞速度,根据平飞时P=D,当飞机的阻力系数取得最小值CD min时,飞行速度达到最大值,即有
(9)
经过计算可知,以推力为限制的飞行速度超过了动压限制和温度限制,对于飞行包线无意义。
3.4 对比验证
将由图10、图13和图14所计算的结果绘制到一张曲线图上并求交集,即为飞机的基本飞行包线,如图15所示。飞行包线的左边界为失速限制,超过左边界时飞机的升力将不足以维持其飞行高度;上边界为静升限,飞机到达静升限时上升率为0,不能够继续爬升;右边界为动压限制和温度限制,超过右边界时飞机结构发生破坏而不能安全飞行。
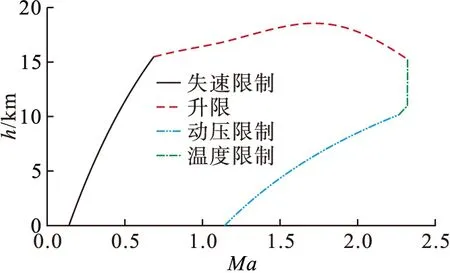
图15 基本飞行包线计算结果
将同类飞机A的飞行包线与计算结果绘制在一张曲线图上进行对比(见图16)。分析可知,本文计算结果与已知飞机A的飞行包线基本相符,说明了计算结果的可靠性;计算结果的左边界偏保守,主要是由于数值模拟计算以及曲线拟合产生的误差造成的;计算结果的上边界及右边界范围更大,这主要是由于该飞机是在飞机A的基础上改进升级而来,推力、结构强度都有相应的提升,计算得到的温度极限值和最大表速较大,包线边界向右上扩展,拥有更大的极限飞行速度。
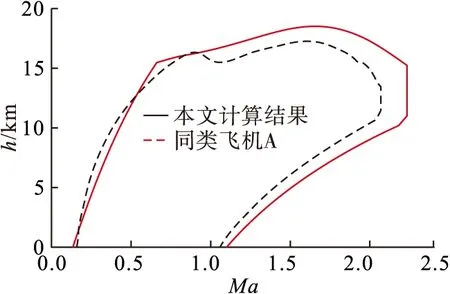
图16 飞行包线对比验证
4 结论
本文通过三维逆向建模建立了飞机的三维几何模型,通过计算流体力学的方法计算分析了其纵向气动特性,并基于气动数据计算了体现飞机基本飞行性能的飞行包线,为该飞机的飞行安全提供了技术支撑,为其空战仿真进行了数据准备。具体结论如下:
1)气动特性方面,采用翼身融合气动布局的该型飞机在小迎角飞行状态下具有较好的巡航性能,升阻比较高,并且飞机的大迎角飞行性能突出,失速迎角在30°左右;
2)飞行包线方面,经过对比验证,计算得到的基本飞行包线能够体现飞机的飞行性能,具有较高的可靠性;
3)本文所做工作探索出了一条从三维逆向建模到气动特性计算、飞行边界求解来研究外军缺乏气动参数飞机飞行性能的完整技术途径,具有较高的通用参考价值,可以应用于其他先进飞行器。

