基于全碳化硅功率组件的变流器母排杂散电感解析计算方法
刘 博 刘伟志 董 侃 马 强 刁利军
基于全碳化硅功率组件的变流器母排杂散电感解析计算方法
刘 博1刘伟志2董 侃2马 强3刁利军1
(1. 北京交通大学电气工程学院 北京 100044 2. 中国铁道科学研究院机车车辆研究所/北京纵横机电技术开发公司 北京 100094 3. 中车长春轨道客车股份有限公司 长春 130000)
碳化硅(SiC)器件的高开关速度使得其对杂散参数更为敏感,容易激发高频振荡和超调。因此需要对功率回路杂散电感进行准确计算,其中以母排电感最为关键。该文首先对现有母排电感计算方法分析比较,并提出一种考虑趋肤效应影响的母排电感计算方法;在此基础上,结合有限元仿真定量分析空间几何参数、器件布局和母排开孔等因素对母排电感的影响,并通过最小二乘逼近得到多异结构母排电感解析计算公式。最后,使用该方法计算1 200V/423A SiC MOSFET测试平台的母排电感,并分别与Ansys Q3D仿真提取结果和实验测试结果对比,结果表明,该方法计算大功率变流器叠层母排杂散电感具有较高的实用性和准确性,可为SiC MOSFET的应用研究和叠层母排的布局设计提供有益支撑。
叠层母排 杂散电感 解析计算 双脉冲测试
0 引言
近年来,碳化硅(Silicon Carbide, SiC)MOSFET凭借导热系数高、阻断电压高等优势在电动汽车[1]、船舶电力[2]和轨道交通[3]等领域获得了广泛应用。由于SiC MOSFET具有良好的开关特性,目前,基于SiC MOSFET的电力电子装置的开关频率已经达到MHz级,很大程度上提升了系统的功率密度[4-5]。但是,SiC MOSFET开关动作时,过大的d/d在与回路电感的作用下感生出较高的电气应力[6],同时还可能导致高频噪声[7]和传导干扰[8]等问题。为了对系统中额外应力和高频振荡等非理想特性进行评估,要对功率回路的杂散电感进行准确提取[9]。
回路电感由器件内部杂散电感、支撑电容寄生电感以及母排电感组成。其中器件杂散电感和支撑电容寄生电感可以由数据手册获得,而母排电感的准确提取一直受到专家学者的关注。目前,母排杂散电感的提取方法主要有数值计算法、测量法和解析法[10]三种:数值计算法主要通过有限元分析或部分单元等效电路的方法求解麦克斯韦方程,结合母排的材料、尺寸等影响因子从而得到电感值,这种方法可以获得影响规律,但需要大量的仿真结果进行归纳,仿真时间太长[11];测量法可以很好地对母排电感进行较为准确的提取,但是却不能解释其背后更深层次的物理意义[12];解析法虽然推导过程较为繁琐,但是计算迅速,同时可以深入地了解母排电感变化的物理机制,为低感母排的优化设计提供理论依据[13]。目前研究主要集中在针对平行双导线和同轴线的分析[14-15],关于平行板电感分析模型的文献较少,文献[16-17]分别提供一种计算公式,但是并未给出详细推导过程和验证。
针对以上问题,本文在前人研究的基础上,建立叠层母排的物理模型,从电感产生的机理出发,进一步考虑高频应用环境影响,得到更高精度叠层母排电感的解析式。基于此,定量分析了结构参数与元器件布局对母排电感的影响,得到多异结构母排的数学模型。最后,设计了一款叠层母排,将解析式计算结果与传统电感提取方法对比,验证了本文提出模型的有效性和正确性,可以为后续叠层母排的优化设计提供一定参考。
1 叠层母排杂散电感计算方法
1.1 传统的杂散电感提取方法
电感是表征回路包含磁能的能力,被定义为
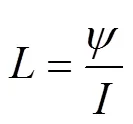
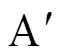
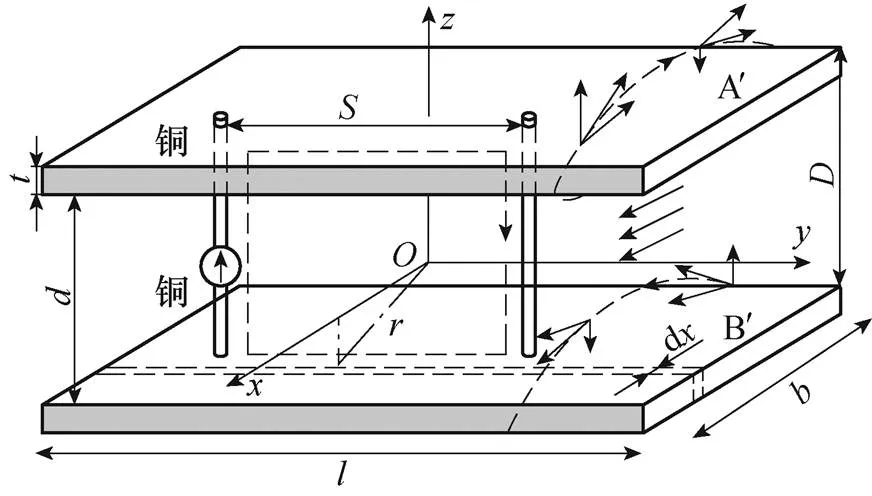
图1 叠层母排模型
传统电感模型将母排近似为双传输线,则内磁通可以表示为
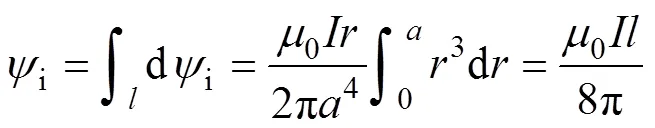
式中,0为磁导率,0=4p×10-7H/m;为导体半径;为积分变量;为导体长度。
内电感可表示为
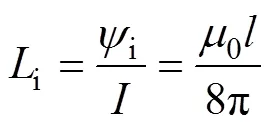

将内、外电感相加可以得到母排计算公式为
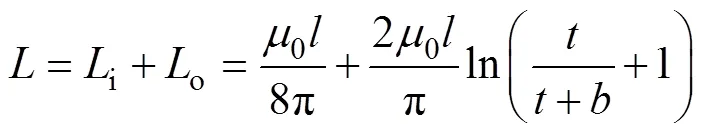
在上述计算过程中,将母排近似为圆直导线进行计算,但由于导体为方形,与圆直导线存在一定误差。此外,对于叠层母排,除导体自感外,互感对总电感的影响也非常大,但该方法未能考虑互感的影响。
1.2 基于安培环路定律的杂散电感提取方法
由于电流镜像流过正负母排,且间距极小,因此叠层母排互感较大,从而降低母排整体电感。但是互感计算方法极其复杂,并且很难给出准确的表达式。文献[18]提出一种计算方法,将正负母排作为整体进行分析。
由于将母排作为整体,在分析磁场时,上、下导体所产生的磁场将互相抵消,对导体内部而言,只存在平行于导体截面的磁场,磁场强度为/(2),根据安培环路定理得
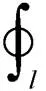
式中,为磁场强度,母排电感表示为
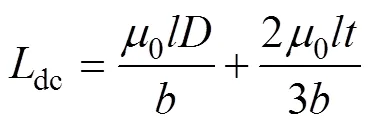
1.3 考虑趋肤效应影响的提取方法
由于开关器件的高频环境,除了母排结构尺寸之外,还应考虑趋肤效应对母排电流分布的影响。1.2节所述计算方法中,未考虑趋肤效应的影响,由于正负铜排间距很小,且趋肤深度远小于母排厚度,因此趋肤效应引入的计算误差较大。由于导体对电流有趋肤效应,电流主要分布在趋肤深度中,趋肤深度表达式为
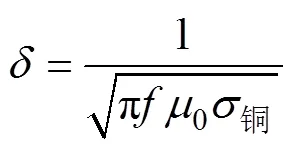
根据式(8)对导体内电感计算公式进行修正,考虑趋肤效应情况下导体内部的磁通环路面积为

磁通量为
母排内电感为
结合式(7)~式(11),给出考虑趋肤效应时的母排电感计算公式为

2 仿真模型与空间几何参数分析
根据式(12),影响叠层母排杂散电感的空间几何参数主要有母排长度、厚度、宽度以及正负母排间距。为了更清楚地认识空间几何参数的影响规律,在Ansys Q3D软件中对母排模型进行仿真。杂散电感的计算、电流路径的仿真均跟变换器工作频率等有一定关系,本文以1 200V/423A的全SiC双脉冲测试平台为研究对象,变换器工作频率为50kHz,平台直流侧采用2支1 120mF的支撑电容并联。
2.1 仿真模型
首先对规则母排进行建模,直流母排的3D模型如图2所示,图2中,母排包括正负母排两层导电层,=400mm,=250mm,=1mm,=0.5mm。
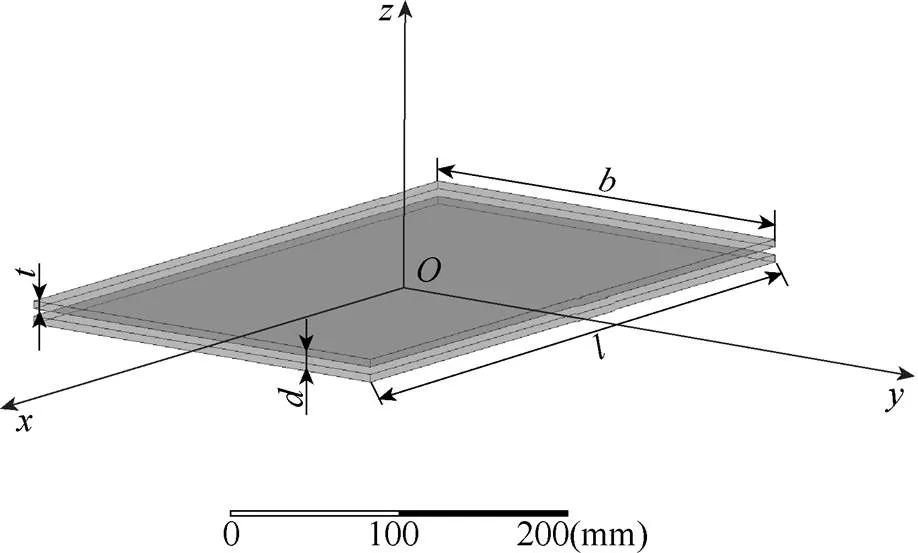
图2 直流母排模型
根据母排的电流流向对正负导电层分别添加激励。每个导电层选取电流流入面作为Source,电流流出面作为Sink,并将整个导电层设置为一个Signal Net。仿真设定的最大频率、最大步长可以采用文献[19]提出的计算公式获得,分析某一几何参数影响时,其他因子按照图2标注尺寸取值。
2.2 电感计算方法验证
使用Ansys Q3D软件对直流母排进行有限元仿真,将本文所提出母排电感计算方法与现有计算方法、仿真结果进行对比。图3为在不同计算模型和仿真条件下,动态调整各影响因子得到的母排电感。M1为传统杂散电感提取方法,M2为基于安培环路定律的计算方法,M3为本文在考虑趋肤效应影响下提出的改进算法。
由图3可以看出,传统算法模型由于未能考虑互感影响,且将矩形母排等效为传输线,导致模型与实际情况差距较大,因此误差较大。方法M2基于安培环路定律的杂散电感提取方法将正负母排作为整体分析内外电感,避免了互感计算复杂的问题,模型具有较高的准确性,但由于未考虑趋肤效应影响,计算结果与仿真结果存在较大误差。
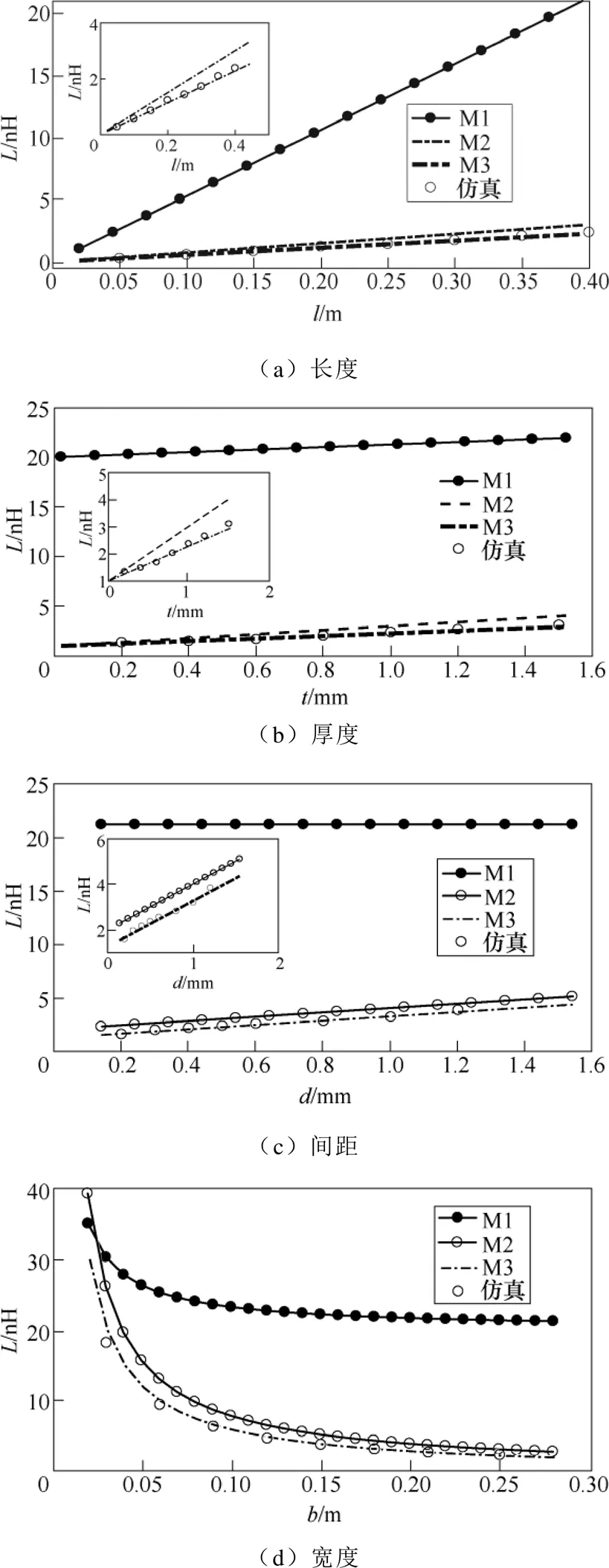
本文在方法M2的基础上,分析了叠层母排的趋肤效应,并通过计算趋肤深度重新确立了磁通回路,进一步给出了母排电感计算公式,计算值与仿真结果基本趋于一致,验证了理论分析的正确性。
2.3 几何参数分析
根据图3中曲线对母排电感与空间几何参数的关系进行分析。在母排间距、厚度和宽度一定的情况下,随着回路长度的增加,母排电感随长度呈线性增长,当长度达到200mm时,母排电感为1.23nH,长度为400mm时,电感为2.38nH,增大了93.5%。宽度为100mm时,电感为5.5nH,增加到200mm时电感降为2.78nH。宽度从30mm到250mm,每增加一倍,降幅约为50%,基本呈线性变化。间距从0.5mm变化到1mm,电感增大了34.9%,厚度从1mm增加到2mm,电感增大了30%。母排越宽,电流路径越宽,将母排剖分为无数细导线,宽度增大则可以理解为并联导线数量增加,电感相应减小。母排长度、厚度和层间距离增加时,正负母排围成的回路面积增加,因此增加了电感量。
根据仿真结果的定量分析,长度和宽度变化对母排的影响最大,但是母排长度和宽度受装置整体布局制约较大,很难成倍变化。设计母排时,应尽量增大器件的横向布局幅度。另外,母排厚度关乎导体载流量,在耐压范围内,应通过减小正负母排距离减小杂散电感。
3 多异结构母排建模分析
实际应用中,叠层母排并不是特定的规则导体,而是受到器件布局、连接等诸多因素影响。基于此,本文通过梳理引起母排电感增量的常见因素,结合Ansys Q3D仿真和最小二乘拟合,从数学角度定量分析母排电感。
3.1 最小二乘拟合原理

令
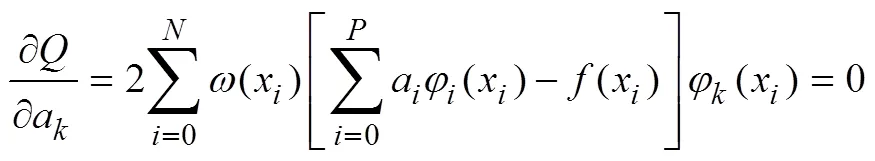
求解公式


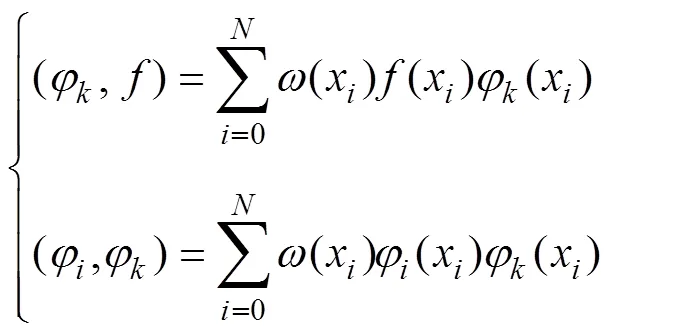
所求多项式为
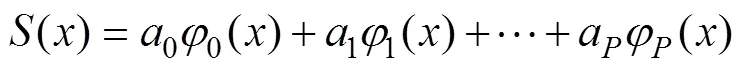
误差二次方和为
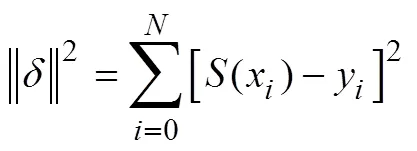
3.2 元器件对母排电感的影响
叠层母排作为功率主回路的连接线,主要接入器件为母线电容、吸收电容和功率器件。功率器件及母排模型如图4所示。由于正负端子之间的距离,图4中电流Ⅱ不存在耦合电流,无论电容还是功率器件,正负接口间距都会导致母排的耦合面积减小,从而影响母排电感。

图4 功率器件及母排模型
为分析元器件正负端口间距对母排电感的影响。在Ansys Q3D中构建3D母排模型(=300mm,=100mm,=1mm,=1mm)。首先,确定元器件相对位置关系。通常情况,功率器件和吸收电容的位置固定,需要对比分析母线电容布局对母排电感的影响。图5列举了四种母线电容布局方式比较。

图5 母线电容布局方式比较
通过仿真得到不同母线电容布局对应母排电感见表1,布局Ⅳ中,耦合面积最小,因此电感最大;布局Ⅲ中,电感最小,相较Ⅰ、Ⅱ两种方式降低了5.8%。因此母线电容布局方式采用布局Ⅲ。
表1 不同母线电容布局对应母排电感

Tab.1 Busbar inductance values for different bus capacitor layouts
通过逐步增大正负端口距离pn,得到不同(=pn/)对应的电感值。一次、二次拟合曲线及其与仿真结果的误差如图6所示,图中,1、2分别为一次、二次拟合对应的误差。从图6可以看出,在母排长度固定的情况下,正负母排电流耦合面积减小,母排电感增大。器件正负端子距离每增大10mm,电感增大约2.3nH,母排电感与端口尺寸近似呈线性关系。
可以看出,器件端口超过15mm后,一次、二次拟合误差均不超过0.7nH。为了尽可能简化计算方法,根据数据拟合结果,给出由元器件正负端口距离引起的电感增量为
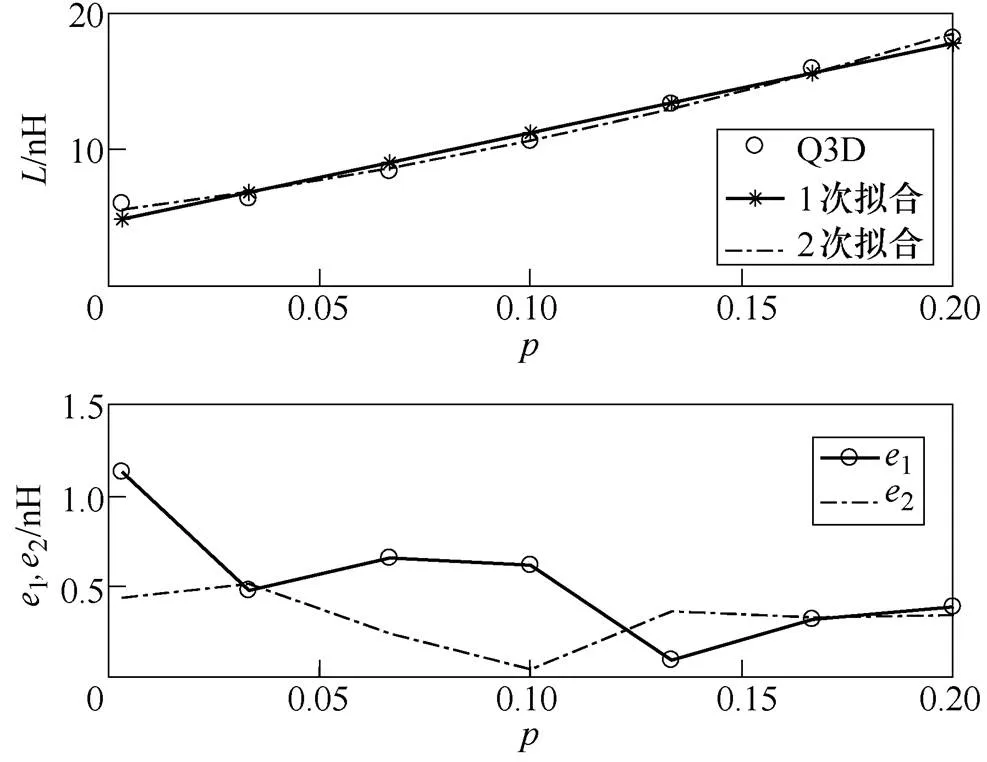
图6 元器件正负端口对电感的影响
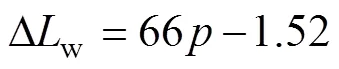
式中,=pn/,pn为元器件正负端口距离。
3.3 开孔对电感的影响
为了使用螺栓将元器件与母排进行安全的电气连接,需要在母排上开孔,另外存在控制线等穿过母排的情况,也需开孔。而开孔将会使得电流路径变窄,从而导致电感增大。开孔有在单层导电体开槽和在双层母排对称开孔两种情况。在3.2节中搭建的母排上做开孔仿真,获得开孔半径为2.5mm到15mm的母排电感值,开孔面积对母排电感的影响和拟合曲线误差如图7所示。
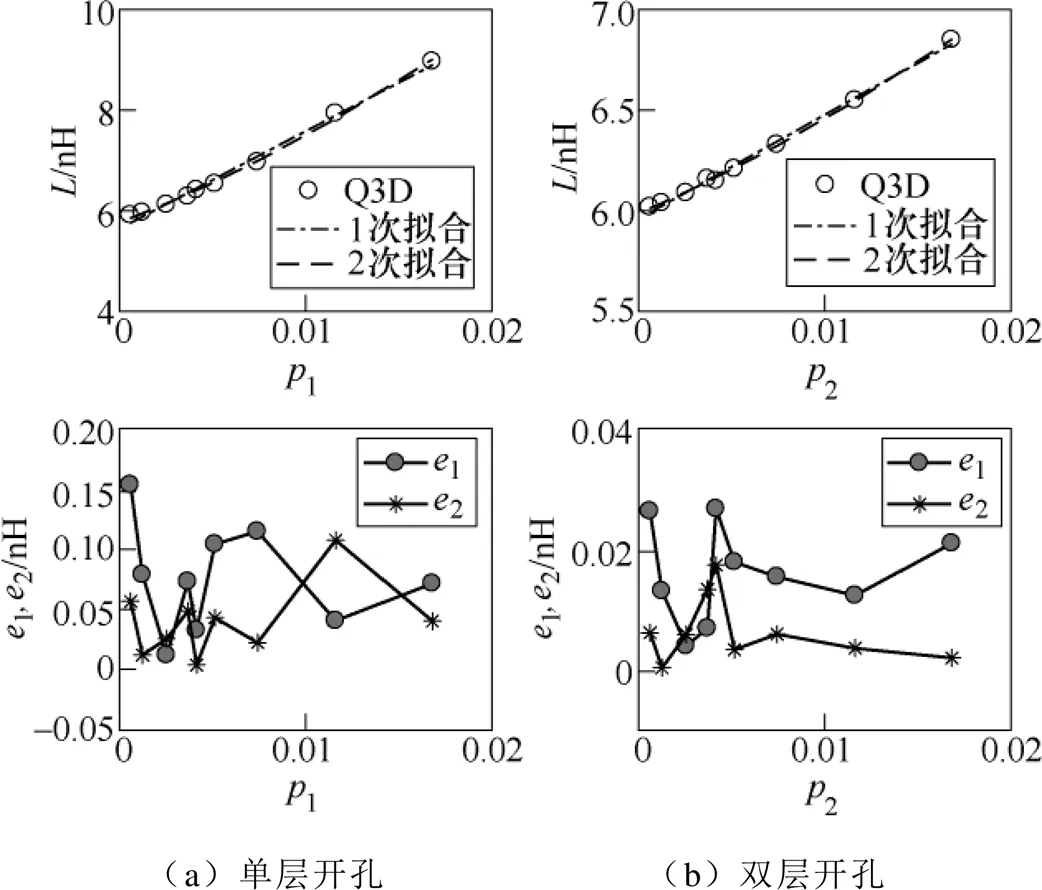
图7 开孔面积对母排电感的影响和拟合曲线误差
对于单层开孔情况,采用一次拟合,最大误差为0.15nH,低于3%,与二次拟合差距不大,为简化运算,采用一次拟合结果。双层开孔时,二次拟合误差明显优于一次拟合,因此采用二次拟合,最大误差小于0.02nH,误差精度可控制在0.22%以内。
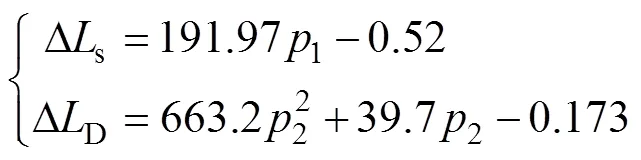
式中,1=1/;2=2/。
双层开孔使得母排电流路径变窄,阻抗变大,电感值出现增加;而单层开孔,除去电流路径的影响之外,耦合面积减小,电感值增大幅度更大。由图7可看出,开孔半径为10mm时,双层孔增量为0.55nH,单层孔电感增量达到1.94nH,为双层孔的3.5倍。
开孔位置和开孔形状将会影响电流路径,进而改变母排电感值。在宽度和长度方向不同位置处开孔(半径相同),图8统计了不同位置开孔对母排电感的影响,b为开孔在母排宽度上的所处位置,l为开孔在母排长度上的所处位置。

图8 不同位置开孔对母排电感的影响
结果表明,开孔位置在宽度上变化时,越靠近中心位置杂散电感越小,最大值bmax=6.17nH,最小值bmin=5.97nH。其原因在于开孔位置靠近边缘时,会使得孔洞两侧阻抗差距较大,电流将会更多地绕行阻抗较小一侧,因此靠近边缘位置开孔将会使得部分电流路径相对增大,电感值增加。而孔洞在长度方向上移动不改变电流路径,因此对母排电感值几乎不产生影响,仿真结果与理论分析一致。综上,根据开孔位置不同,式(18)母排增量公式应乘以相应的调节系数b。
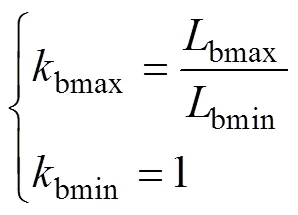
孔洞改变电流路径,因此应考虑开孔形状对母排电感的影响。图9列举了四种不同开孔形状及其电流分布(孔洞面积相同),采用Ansys Q3D仿真得到母排电感见表2,与C、D两种类型相比,A、B两种开孔方式的电感最大能降低3.55%,因此在母排开孔时应尽量选择A或B。本文开孔分析以圆孔为例,对于其他开孔类型对应的电感增量应乘以调节系数S,S=0.965~1。
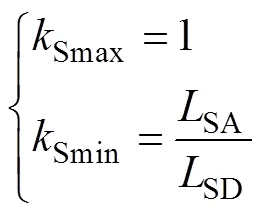
式中,SA、SD分别为长方形开孔和圆形开孔时的母排电感。
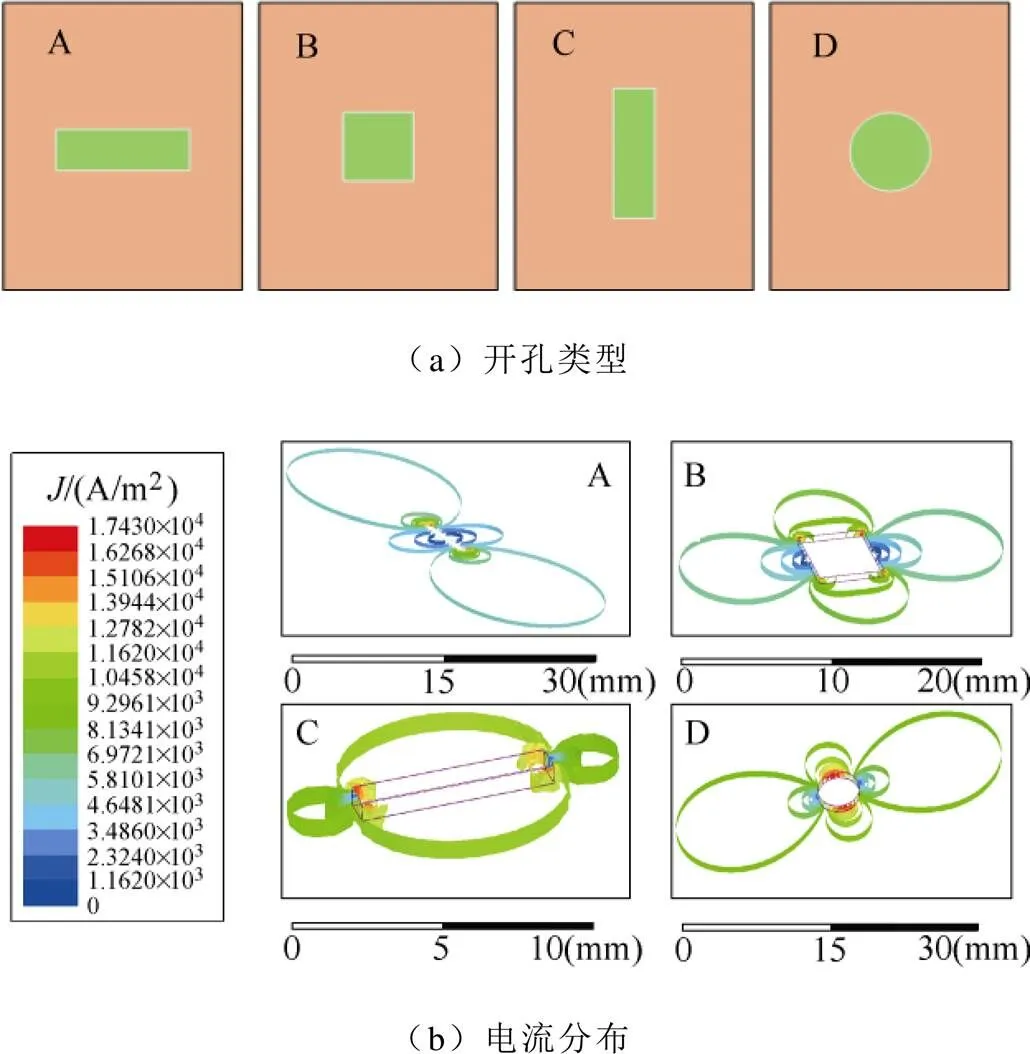
图9 不同开孔形状及其电流分布
表2 各开孔形状下的母排电感

Tab.2 Busbar inductance values under each opening shape
3.4 叠层母排数学模型
规则形状的叠层母排电感可以由式(12)进行计算。综合元器件布局、尺寸和开孔位置、形状、大小等因素对电感的影响分析,给出多异结构叠层母排的电感计算方法为
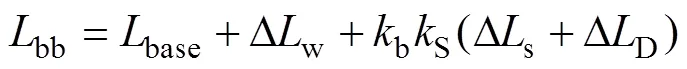
式中,base为规则形状母排电感。
4 方法验证
为评估理论分析的正确性,以1 200V/423A的SiC MOSFET双脉冲测试平台为例,对本文提出的叠层母排计算方法进行验证。
4.1 母排模型和实验平台
双脉冲测试平台的母排俯视图和侧视图如图10所示,图中标注尺寸单位为mm。
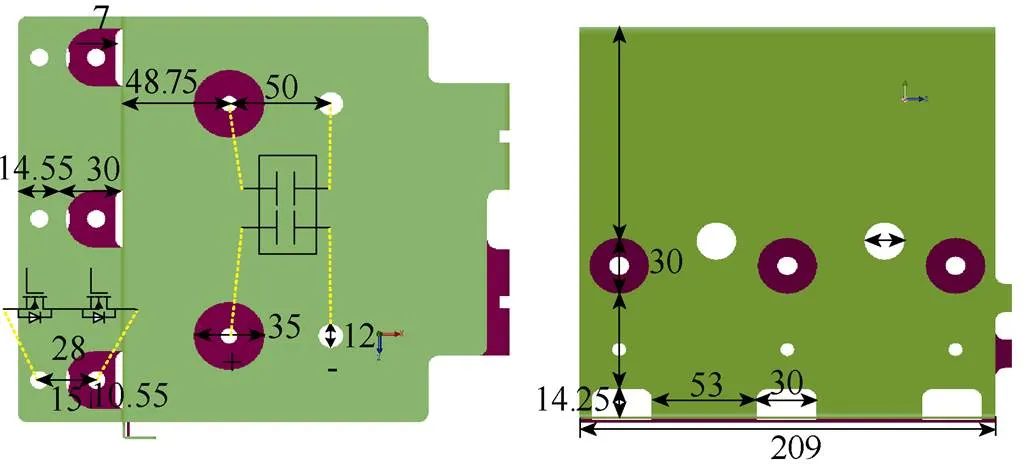
图10 叠层母排模型
双脉冲测试平台如图11所示。图11b中,双脉冲测试平台按照图11a所示的电路搭建,图中,T0~T3为4个测试点。其中,被测开关器件SiC MOSFET使用的是Cree公司生产的CAS300M12BM2;驱动板使用Agile Switch的62EM1-62mm;示波器采用的是YOKOGAWA的DLM2024,带宽200MHz。电流采用罗氏线圈获得;双脉冲信号由Firstack的双脉冲测试仪获得。

图11 双脉冲测试平台
4.2 模型验证
测试过程中使用电压探头测量SiC MOSFET两端电压03和支撑电容两端电压13。使用罗氏线圈测量漏极电流d。图12为700V/300A工况下双脉冲实验波形,利用该过程计算母排电感。

图12 关断过程波形
母排电感可以采用关断电流下降斜率dd/d和关断电压过程电压尖峰peak计算,即
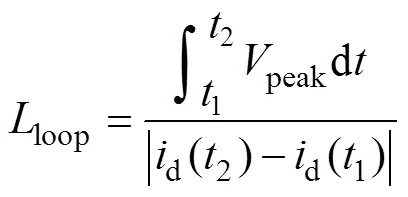
功率回路电感主要包括支撑电容寄生电感sn、母排电感bb(bb=bb1+bb2)、源极电感S和漏极电感D四部分,其中,bb1、bb2分别为正负母排电感。因此母排电感为
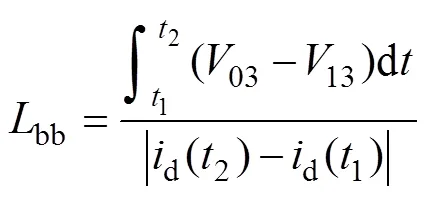
在杂散电感的提取实验中存在很多非理想因素,如电压、电流的读数误差,电流变化率选取时段不同造成偏差。表3统计了700V/300A工况下回路中各部分杂散参数提取结果,可以看出,母排电感值偏低,而支撑电容寄生电感和功率模块寄生电感偏高,这是由于在测试过程中将电压探头夹在母排上,人为缩短了母排回路,从而导致支撑电容寄生电感和器件测量结果偏高,在计算叠层母排电感时,回路电感采用实验测量值,器件寄生电感d和支撑电容寄生电感sn采用数据手册值(器件寄生电感d=s+D,回路电感loop=sn+bb+d),叠层母排的计算结果为bb=60.55-20-15=25.55nH。
表3 各部分电感
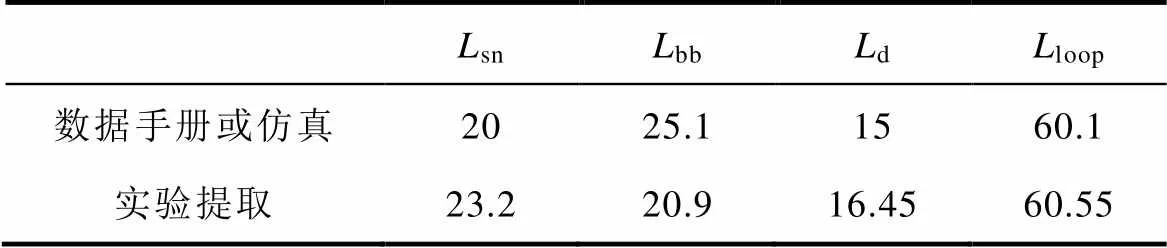
Tab.3 Inductance of each part (单位: nH)
目前,叠层母排电感的常规获取手段包括有限元仿真、实验测量和模型计算三种。表4给出三种提取方法下图10所示母排的电感,并以本文方法为标准值进行误差分析,与Ansys Q3D仿真结果和实验测量结果进行对比。
表4 不同方法获得母排电感

Tab.4 Different methods to obtain the busbar inductance value
本文计算方法与仿真和实验结果基本吻合,具有较高精度,验证了本文所提出叠层母排电感计算方法的有效性。
5 结论
本文针对叠层母排电感解析计算问题开展研究。通过仿真分析与数学模型相结合,得到了多异结构叠层母排电感的解析公式,主要包括以下内容:
1)分析了高频环境下,趋肤效应对母排电感的影响,并给出考虑趋肤深度的叠层母排电感数学计算方法,结果表明:高频环境下,电流主要流经导体表面,本文给出的规则叠层母排计算公式误差低于5%,准确度得到较大提升。
2)以双极板叠层母排为研究对象,研究了功率器件布局和母排开孔位置、大小等对母排电感的影响,并结合Q3D仿真定量的给出电感增量解析公式。结合规则母排模型,给出多异结构母排电感解析计算方法。
3)采用本文所提计算方法对基于SiC MOSFET双脉冲测试平台的多异结构叠层母排电感进行计算,与实验结果误差为7.26%,不足2nH,验证了该方法的有效性和准确性。
[1] Millan J, Godignon P, Perpina X, et al. A survey of wide bandgap power semiconductor devices[J]. IEEE Transactions on Power Electronics, 2014, 29(5): 2155-2163.
[2] Yin Shaobo, Xia Jinhui, Zhao Zhen, et al. Fast restarting of free-running induction motors under speed-sensorless vector control[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 6124-6134.
[3] Diao Lijun, Du Huiqing, Shu Zhan, et al. A comparative study between AI-HM and SPD-HM for railway auxiliary inverter with pulsating DC link[J]. IEEE Transactions on Industrial Electronics, 2017, 65(7): 5816-5825.
[4] 张建忠, 吴海富, 张雅倩, 等. 一种SiC MOSFET谐振门极驱动电路[J]. 电工技术学报, 2020, 35(16): 3453-3459.
Zhang Jianzhong, Wu Haifu, Zhang Yaqian, et al. A resonant gate driver for SiC MOSFET[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(16): 3453-3459.
[5] 王莉娜, 马浩博, 袁恺, 等. SiC MOSFET半桥电路开关瞬态过电流、过电压建模与影响因素分析[J]. 电工技术学报, 2020, 35(17): 3652-3665.
Wang Lina, Ma Haobo, Yuan Kai, et al. Modeling and analysis of influencing factors of transient over- current and overvoltage in SiC MOSFET half-bridge circuit switches[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3652-3665.
[6] 朱义诚, 赵争鸣, 王旭东, 等. SiC MOSFET与SiC SBD换流单元瞬态模型[J]. 电工技术学报, 2017, 32(12): 58-69.
Zhu Yicheng, Zhao Zhengming, Wang Xudong, et al. Transient model of switching unit between SiC MOSFET and SiC SBD[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 58-69.
[7] Sakairi H, Yanagi T, Otake H, et al. Measurement methodology for accurate modeling of SiC MOSFET switching behavior over wide voltage and current ranges[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7314-7325.
[8] 江师齐, 刘艺涛, 银杉, 等. 基于噪声源阻抗提取的单相逆变器电磁干扰滤波器的设计[J]. 电工技术学报, 2019, 34(17): 3552-3562.
Jiang Shiqi, Liu Yitao, Yin Shan, et al. Design of electromagnetic interference filter for single-phase inverter based on noise source impedance extra- ction[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3552-3562.
[9] 谢佳季, 游小杰, 郭希铮, 等. 基于SiC MOSFET的辅助变流器应用研究[J]. 电源学报, 2017, 15(2): 67-76.
Xie Jiaji, You Xiaojie, Guo Xizheng, et al. Appli- cation of auxiliary converter based on SiC MOSFET[J]. Journal of Power Supply, 2017, 15(2): 67-76.
[10] Shi Yuliang, Xie Ren, Wang Lu, et al. Switching characterization and short-circuit protection of 1200V SiC MOSFET T-type module in PV inverter appli- cation[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 9135-9143.
[11] 金祝锋, 李威辰, 胡斯登, 等. 大容量电力电子装置中母排杂散电感提取方法的优化研究[J]. 电工技术学报, 2017, 32(14): 1-7.
Jin Zhufeng, Li Weichen, Hu Sideng, et al. Optimi- zation study of bus bar stray inductance extraction method in large-capacity power electronic devices[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 1-7.
[12] Reigosa P D, Iannuzzo F, Luo H, et al. A short-circuit safe operation area identification criterion for SiC MOSFET power modules[J]. IEEE Transactions on Industry Applications, 2017, 53(3): 2880-2887.
[13] Hazra S, Madhusoodhanan S, Moghaddam G K, et al. Design considerations and performance evaluation of 1200V 100A SiC MOSFET-based two-level voltage source converter[J]. IEEE Transactions on Industry Applications, 2016, 52(5): 4257-4268.
[14] 刘欣, 王利桐, 梁贵书, 等. 压装组件中圆柱形母线的部分电感计算方法[J]. 电工技术学报, 2020, 35(增刊1): 1-9.
Liu Xin, Wang Litong, Liang Guishu, et al. Com- puting method for partial inductance of cylindrical busbar conductor[J]. Transactions of China Electro- technical Society, 2020, 35(S1): 1-9.
[15] Ruehli, Albert E, Antonini, et al. Skin-effect loss models for time- and frequency-domain PEEC Solver[J]. Proceedings of the IEEE, 2013, 101(2): 451-472.
[16] 阮杰, 刘畅, 李广卓, 等. 适用于器件并联型ANPC拓扑的低感叠层母排设计方法[J]. 高电压技术, 2019, 45(7): 2093-2100.
Ruan Jie, Liu Chang, Li Guangzhuo, et al. A low inductance laminated bus design method for device parallel ANPC topology[J]. High Voltage Engineering, 2019, 45(7): 2093-2100.
[17] Caponet M C, Profumo F, De Doncker R W, et al. Low stray inductance bus bar design and construction for good EMC performance in power electronic circuits[J]. IEEE Transactions on Power Electronics, 2000, 17(2): 225-231.
[18] 刘峰, 马伯乐, 杨光. 大功率变流器模块主电路杂散电感分析[J]. 机车电传动, 2013, 1(6): 15-19.
Liu Feng, Ma Bole, Yang Guang. Stray inductance analysis of main circuit of high-power converter module[J]. Locomotive Electric Drive, 2013, 1(6): 15-19.
[19] 朱俊杰, 原景鑫, 聂子玲, 等. 基于全碳化硅功率组件的叠层母排优化设计研究[J]. 中国电机工程学报, 2019, 39(21): 6383-6393.
Zhu Junjie, Yuan Jingxin, Nie Ziling, et al. Research on optimal design of laminated busbars based on full silicon carbide power modules[J]. Proceedings of the CSEE, 2019, 39(21): 6383-6393.
Analytical Calculation Method for Stray Inductance of Converter Busbar Based on Full Silicon Carbide Power Module
12231
(1. School of Electrical Engineering Beijing Jiaotong University Beijing 100044 China 2. Locomotive & Vehicle Research Institute of China Academy of Railway Sciences Beijing Zongheng Electro-Mechanical Technology Co. Ltd Beijing 100094 China 3. CRRC Changchun Railway VEHICLES Co. Ltd Changchun 130000 China)
The high switching speed of silicon carbide (SiC) devices makes them more sensitive to stray parameters and easily excites high-frequency oscillations and overshoot. Therefore, it is necessary to accurately calculate the stray inductance of the power circuit, and the busbar inductance is the most critical. This paper first analyzes and compares existing busbar models, and proposes a calculation method of busbar inductance that takes into account the skin effect. On this basis, based on finite element simulation, the influence of spatial geometric parameters, device layout and busbar openings on the busbar inductance is quantitatively analyzed. Moreover, through the least squares approximation, the analytical calculation formula for the inductance of the busbar with multiple different structures is obtained. Finally, this method is used to calculate the bus inductance of the 1 200V/423A SiC MOSFET test platform, and the results are compared with Ansys Q3D simulation results and experimental results. It is shown that this method has high practicality and accuracy in calculating the stray inductance of high-power converter laminated busbars, which can provide useful support for the application research of SiC MOSFETs and the layout design of laminated busbars.
Laminated busbars, stray inductance, analytical calculation, double-pulse-test
TM46
10.19595/j.cnki.1000-6753.tces.L90080
国家重点研发计划项目(2020YFF0304103)和北京市科委项目(Z181100004418005)资助。
2020-06-20
2021-01-06
刘 博 男,1996年生,硕士,研究方向为新型电力电子器件应用。E-mail: 18121460@bjtu.edu.cn
刁利军 男,1980年生,教授,博士生导师,研究方向为电力电子在轨道交通方向的应用。E-mail: ljdiao@bjtu.edu.cn(通信作者)
(编辑 陈 诚)

