变电站软导线端部力矩的计算

(中国电力工程顾问集团华东电力设计院有限公司，上海 200001)

0 引言

在变电站设计中，计算软导线两端的约束反力时，通常只考虑力而不考虑力矩，这是因为通常认为软导线是绝对“柔软”的，即认为软导线只有抗拉刚度，没有抗弯强度[1-3]。但实际情况并非如此，尤其是当软导线直径较大，或者采用多分裂导线时，软导线的抗弯强度是不可忽略的。由于软导线具有抗弯强度，因此导线端部就会存在约束力矩，该力矩作用在设备的端子板上，可能对端子板造成损坏。

本文考虑了软导线的抗弯强度后，推导了软导线的力学方程，给出了端部力矩的计算方法，并提供了几个工程算例。

1 软导线的力学模型

建立坐标系，令Y轴垂直于地面，X轴平行于地面，软导线两端点的坐标分别为(0，0)和(L，h)，两端点与地面的夹角分别为θ1和θ2。假设导线只受重力作用，单位长度的导线所受重力为q。如图1所示。

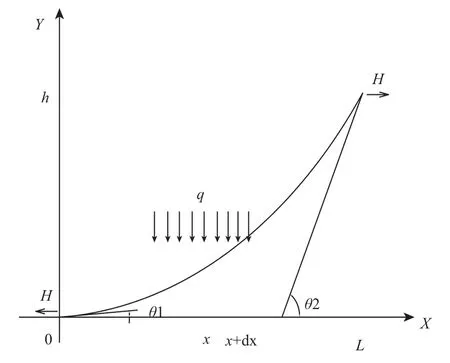
图1 软导线示意图

取软导线中的一个“dx”微段作分析，受力如图2所示；由于考虑到导线的抗弯强度，微段的两端不仅受力的作用，还有力矩作用。同理，导线所受的水平力和垂直力的合力方向不再沿导线的切线方向，这一点是与未考虑抗弯强度时有区别的。

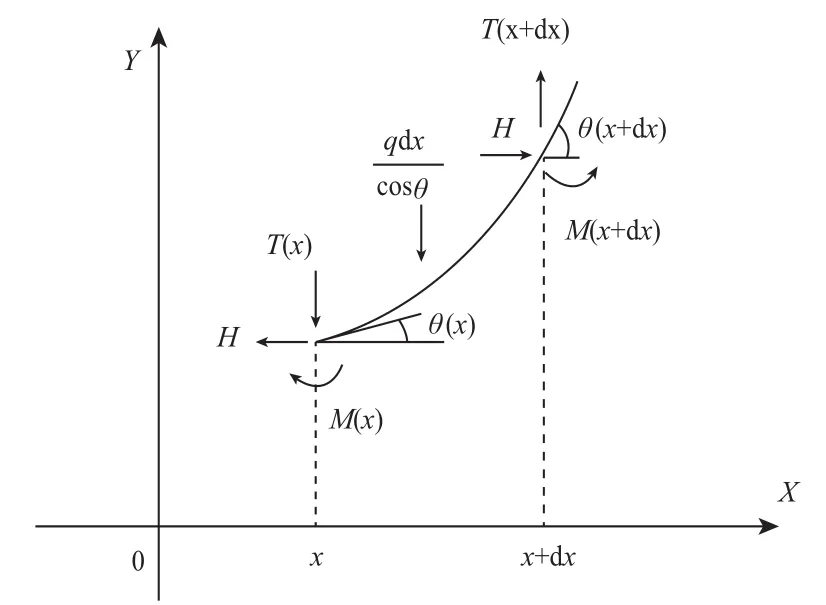
图2 软导线受力分析

根据受力和力矩平衡条件，有如下的关系式。

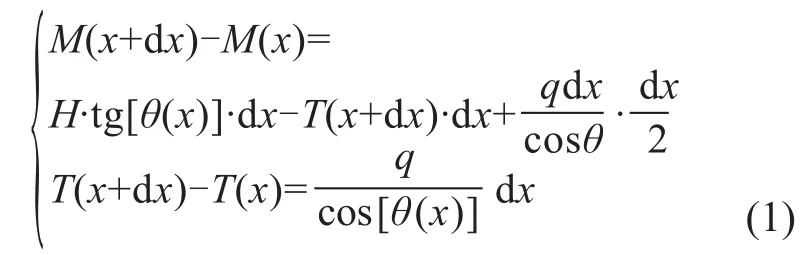
设软导线的方程为y=f(x)，则(1)式中的

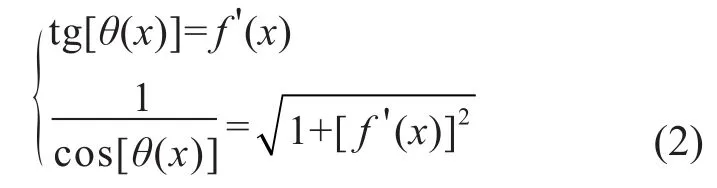
将(2)式代入(1)式，同时将(2)式右端的“dx”移到左端，并略去高阶无穷小量，可得：

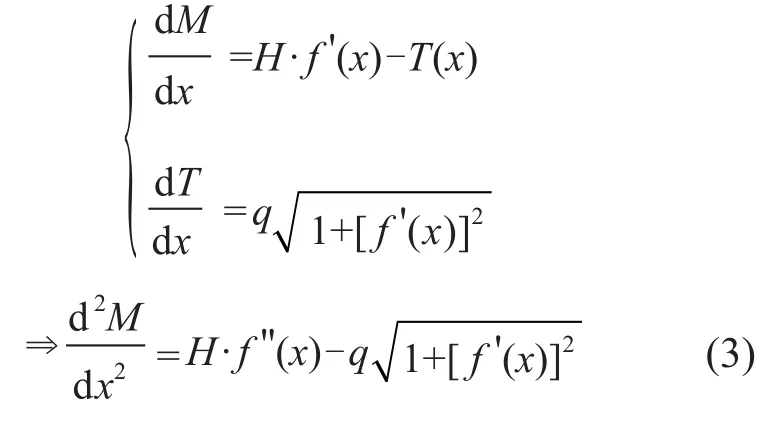
将导线看作一根杆件，根据材料力学[4]，杆件上的弯矩可表达为：

其中E为材料的弹性模量，I为杆件的截面系数。

将(4)式代入(3)式，得到：

式(5)是考虑到抗弯强度后软导线的力学方程。这是一个四阶的非线性微分方程，而且方程中还有一个未知数“H”，即软导线所受的水平力；要解这样一个微分方程，需要5个已知条件。导线两端的边界条件共有4个，即两端的函数值和一阶导数值；导线的弧垂可以作为第5个已知条件。

若I=0，即忽略软导线的抗弯强度，则式(5)退化为常见的软导线方程；若H=0，即导线端部为水平滑动连接、水平方向上没有约束，则式(5)退化为常见的支撑管母线方程。

2 软导线方程的求解

式(5)是软导线精确的微分方程，但由于是非线性的，求解困难，因此在工程应用时需要对其作一定的近似。方程中的非线性主要来源于项，当导线的弧垂与导线长度相比较小时，，将该近似表达式代入式(5)，并令则软导线的方程可近似为一个线性微分方程[5-7]。

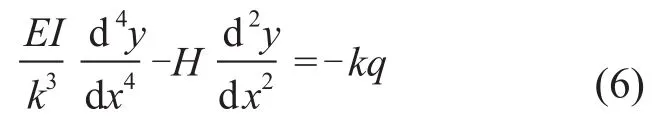
式(6)是一个四阶的线性微分方程，其通解为：

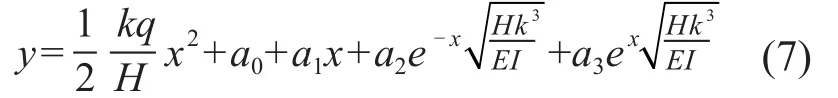
其中a1，a2，a3，a4为待定系数，由微分方程的边界条件决定。软导线微分方程的边界条件如下。

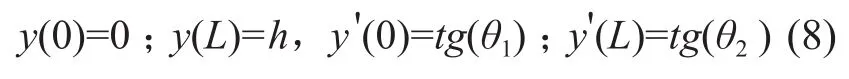
将边界条件代入式(7)，可以求解出待定系数如下。

求解出四个待定系数后，仍存在一个未知数“H”，即导线的水平力未知。通常软导线的弧垂是已知的，可通过弧垂反推出“H”，具体方法可采用试凑法，这里不赘述。

根据式(4)，软导线任一点的力矩为：

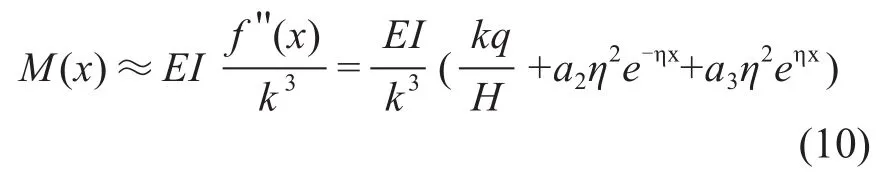
根据式(3)，导线任一点的垂直力为：

工程中的软导线多为绞线，将绞线近似看作一“束”子导线构成的集合体，忽略子导线间的摩擦，则软线的截面系数的计算方法如下[8-9]：

式中：n为绞线中包含的子导线根数；r为子导线的半径，m。

3 算例

根据上文的推导结果，下面给出几个工程实例做计算。

1)某110 kV设备连线，相关计算输入及计算结果见表1。

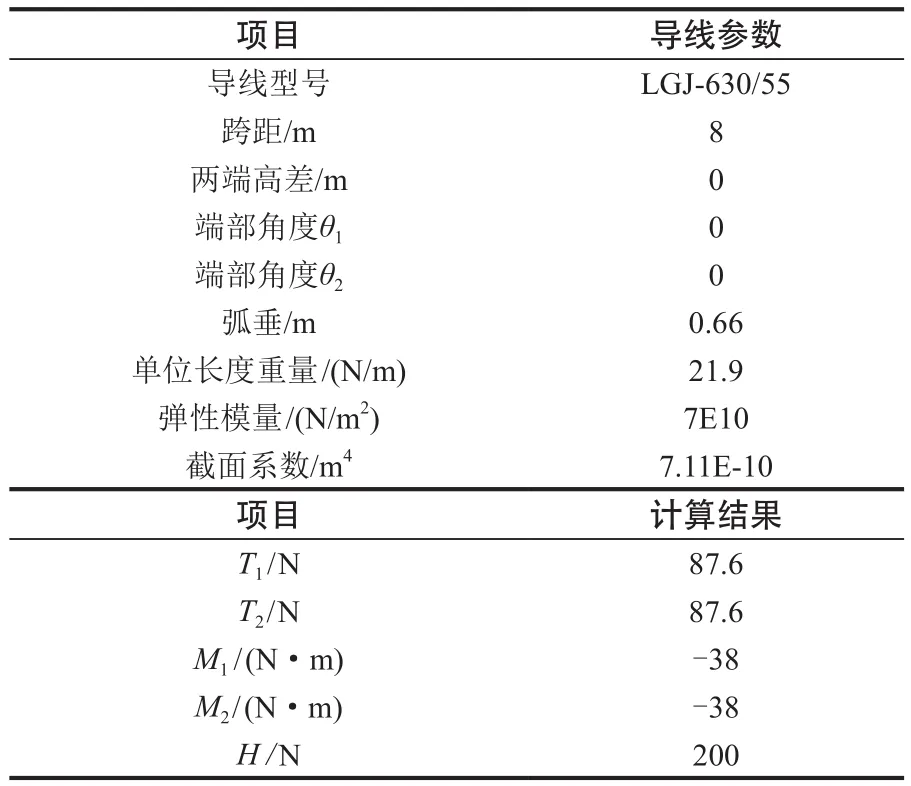
表1 某110 kV设备连线计算结果

2)某220 kV设备连线，相关计算输入及计算结果见表2。

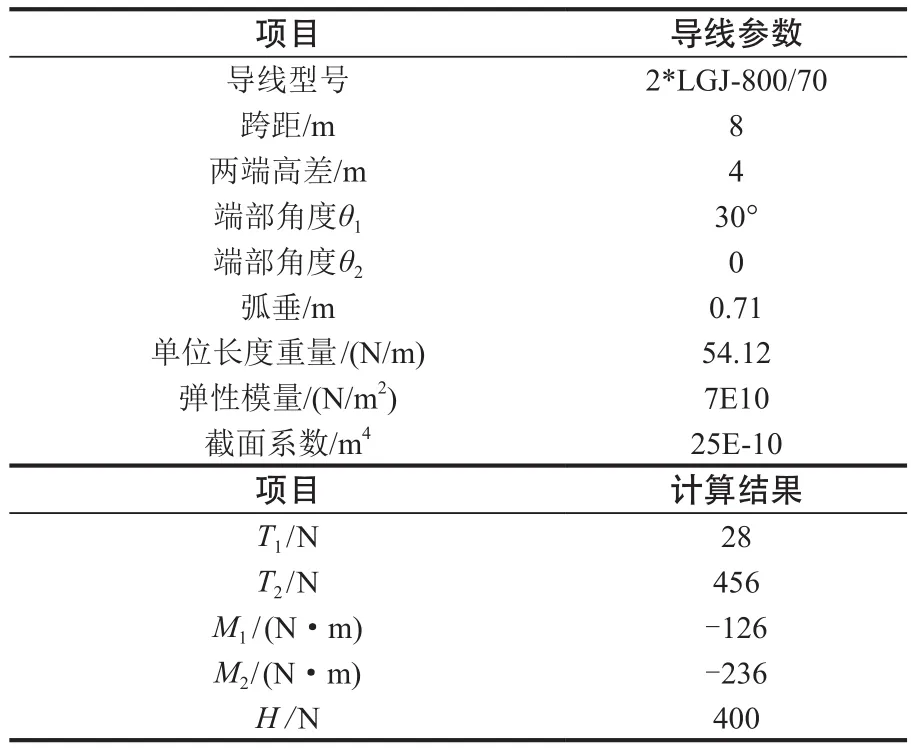
表2 某220 kV设备连线计算结果

3)某500 kV设备连线，相关计算输入及计算结果如表3～表5所示。

表3 金具角度与导线自然弯曲角度相反时设备连线计算结果

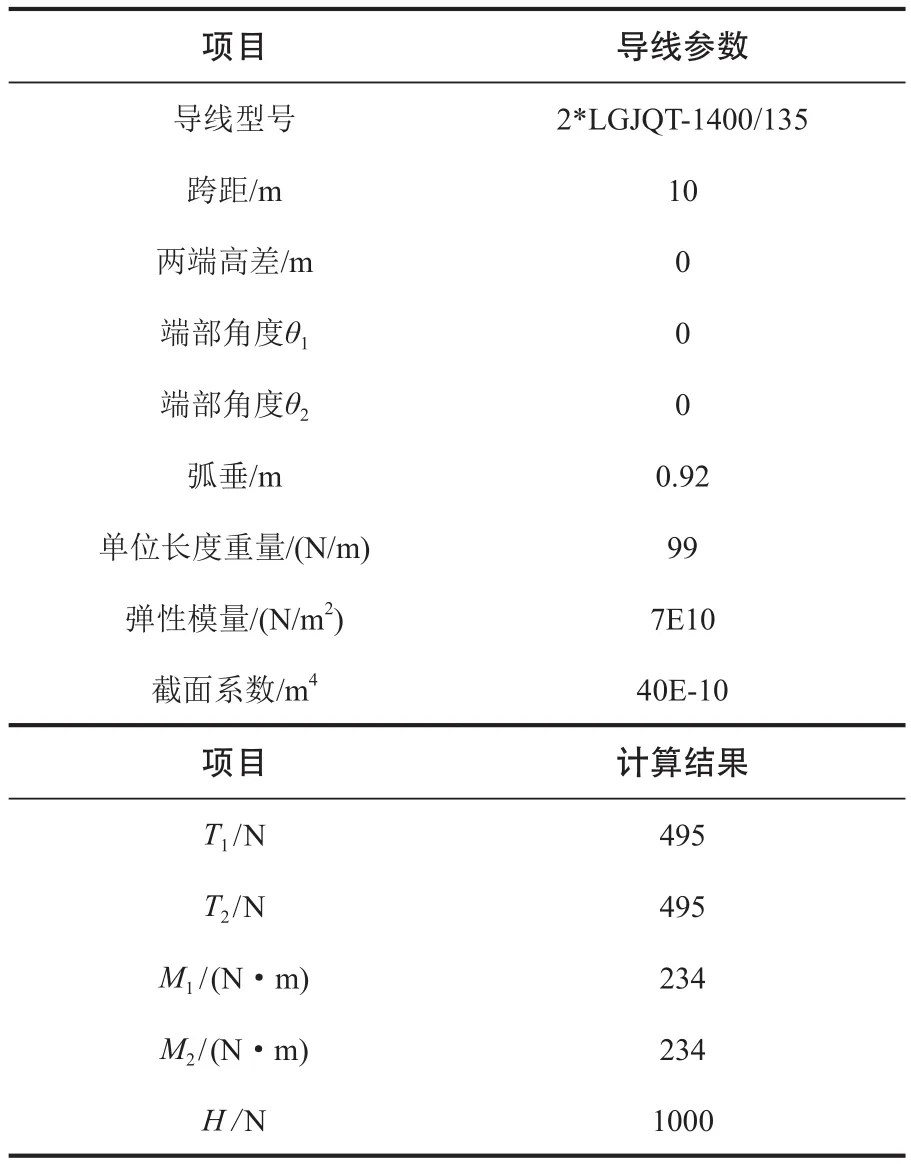
表4 金具角度为零度时设备连线计算结果

表5 金具角度与导线自然弯曲角度相同时设备连线计算结果

由表1～表5可以看出，导线端部的力矩随着导线重量的增加而增加，随着导线抗弯强度的增加而增加。

对比表3～表5可以看出，同样跨度和导线重量下，适当调整导线端部的角度，使其尽量与导线自然弯曲角度相同，可以明显降低端部力矩。实际工程中，调整导线端部的角度可以通过选择金具的角度来实现。

4 结论

计及软导线的抗弯强度后，本文推导了软导线的力学表达式，为一个四阶的非线性微分方程。结合工程实际，引入一定的近似条件，本文又将微分方程线性化，并给出了它的解。

通过几个算例可看出，随着导线重量和抗弯强度的增加，导线端部的力矩由数十N·m增大到了数百N·m；因此在工程设计中，导线端部力矩不应该被忽略处理，而应纳入设备的招标规范中，否则设备端子板有可能被力矩损坏。另外，合理选择设备端子板连接金具的角度可以有效降低端部力矩。

本文共有两处近似，在实际应用中会造成一定的误差：

2)计算软导线截面系数时，将其看作一“束”子导线构成的集合体，未考虑子导线绞绕的效果及相互的摩擦力；对于多分裂导线，也未考虑间隔棒的影响。后续应结合理论和试验开展软导线截面系数的研究。