基于最小构造模型的地空瞬变电磁一维正反演技术研究

张振雄, 易国财, 王仕兴, 郭 明, 何 可, 张赛民, 毛立峰

(成都理工大学 地球勘探与信息技术教育部重点实验室，成都 610059)

0 引言

地空瞬变电磁法(Ground-airborne TEM)，是采用接地长导线源供以阶跃电流信号从而在空间产生一次磁场，一次磁场通过激励地下地质体感应出变化的二次场，通过空中的接收线圈接收二次场信号，从而达到探测地下目标体的目的。地空瞬变电磁系统在上世纪50年代开始研究，直到90年代后才被应用于海岸线结构调查、火山结构调查、地下断层调查等[1-3]。国内的起步研究较晚，阳贵红[4]对电性源低空探测系统进行了研究，总结了数据预处理的若干方法；嵇艳鞠[5]用无人飞艇进行了首次试飞探测，验证了地空瞬变电磁的可行性；李貅[6]提出了地空瞬变电磁逆合成孔径成像技术，改进了传统的单点处理方式；高嵩等[7]提出了地空瞬变电磁信号的模型, 并在原有噪声的基础上加入了无人机干扰和接收线圈运动的噪声，增加了系统的灵敏度和精确性等。

瞬变电磁的一维正反演技术在上世纪40年代-60年代由前苏联人首先实现，并建立了具体的解释理论和工作方法，使得瞬变电磁真正进入了实用阶段。李吉松等[8]研究了电偶源瞬变测深的一维正演和视电阻率响应；翁爱华等[9]讨论了提高长偏移距瞬变电磁测深晚期数值响应计算精度的计算方法；闫国翔[10]对带激电效应的电性源瞬变电磁法进行了一维正反演研究。目前而言，瞬变电磁的二维、三维正反演技术计算量过大，耗费时间过长，难以短时间内应用于瞬变电磁资料的解释，所以一维正反演技术仍是现在瞬变电磁解释资料的首要选择。

笔者通过对长导线源一维正演公式的梳理，经过Hankel变换、Gauss积分和频-时转换，得出了长导线源的一维时间域响应公式，并通过解析解和数值解的对比验证了正演程序的准确性。不同于李锋平[11]烟圈反演的定性研究和张澎[12]采用最平坦模型约束的自适应正则化反演。笔者对比了三种不同约束模型对目标层的识别能力，将最小构造模型约束下的正则化反演方法，运用于某滑坡实测数据的反演中，结果表明，最小构造约束模型下的自适应正则化反演，可以较为准确地反映工区的地下电阻率分布，为搭载该方法的地空瞬变电磁系统应用于其他工区开了先例。

1 一维正演研究

1.1 正演算法

对于水平层状一维频率域垂直磁场正演公式有：

(1)

式中：Hz为垂直分量的频率域磁场响应(A/m)；ω为采样角频率(rad/s)；I为电流强度(A)；L为长导线源长度的一半(m)；R为偏移距(m)；rTE是TE模式下的反射系数；z是接收线圈距离地面的高度(m)；λ是积分变量；J1是一阶贝塞尔函数。

为求得时间域感应电动势，需对式(1)进行Hankle变换和Gauss积分，然后通过频-时转换得到时间域感应电动势。

笔者通过G-S变换将地空瞬变电磁频率域响应转化为时间域响应得：

(2)

式中：Vz为感应电动势(V)；Km为G-S变换的系数；Sm是决定于计算机位数的正偶整数。

1.2 算法正确性验证

通过对比数值解跟解析解吻合程度和相对误差验证正演程序的准确性。设定误差公式为式(3)。

Re= (Sn-Sa)/Sa×100%

(3)

Nabighian等[13]推导出的均匀大地接地长导线源瞬变电磁响应的表达式为式(4)。

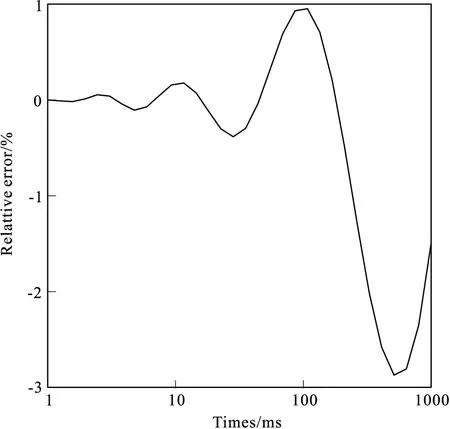
图2 偏移距1 400 m相对误差曲线Fig.2 Relative error curve of 1 400 m

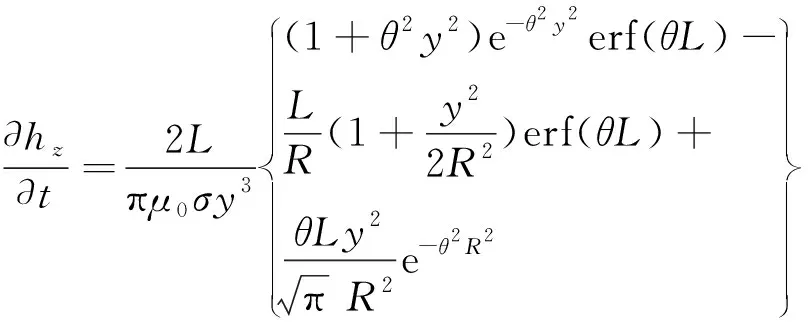
(4)

图3 偏移距3 000 m数值解与解析解对比Fig.3 Comparison of numerical solution and analytic solution with offset of 3000 m

图4 偏移距3 000 m相对误差曲线Fig.4 Relative error curve of 3 000 m

从图1～图4可以看出，相同模型下数值解与解析解的曲线拟合程度较好。偏移距Y=1 400 m的模型中，1 ms～100 ms的相对误差在1%以内，100 ms以后的相对误差值最大只有2.8%；偏移距Y=3 000 m的模型中，1 ms～100 ms的相对误差在0.4%以内，100 ms以后的相对误差值最大只有0.9%，满足正演精度要求。两个模型和Nabighian[13]正演给出的模拟结果吻合程度较好，从而定量地验证了正演程序数值计算的正确性。

1.3 正演响应分析

理论设置电阻率为20 Ω·m和200 Ω·m的均匀半空间模型。线源长度为1 000 m；发射电流为20 A；接收线圈有效面积为1000 m2；接收点坐标为(0，200，0)，并绘制了其不同时刻的场值切片图(图5、图6)。

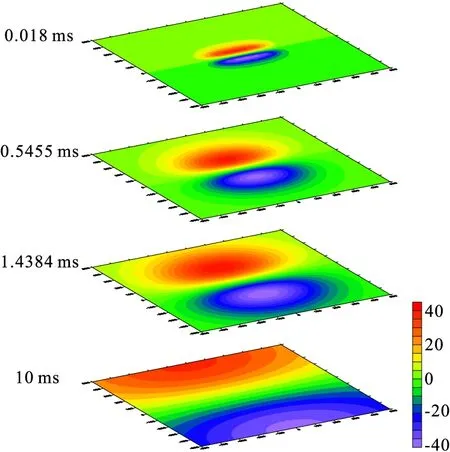
图5 均匀半空间20 Ω·m正演场值切片Fig.5 Uniform half space 20 Ω·m forward field value

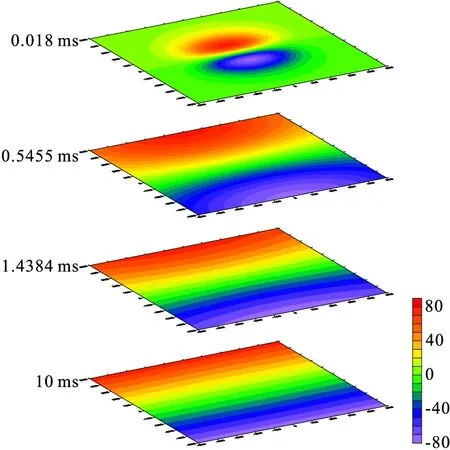
图6 均匀半空间200 Ω·m正演场值切片Fig.6 Uniform half space 200 Ω·m forward field value

对比图5、图6可以发现，均匀半空间的电磁场在低阻地质体中扩散速度慢且场值衰减慢，在高阻地质体中扩散速度快且场值衰减快。综合两张切片图，随着时间增加，正演得到的响应值呈指数衰减，且衰减规律与Nabighian的烟圈理论相符合[13]。

2 自适应正则化反演

2.1 反演原理

目标函数：

φ(m)=φ1(m)+λφ2(m)

(5)

式中：φ(m)为总目标函数;φ1(m)为观测数据目标函数;φ2(m)为模型约束目标函数;λ为正则化因子；m为模型向量。

观测数据目标函数φ1(m)可表示为式(6)。

φ1(m)=‖W1(Δd)‖2

(6)

其中:Δd是观测数据与理论响应差向量;W1为数据加权矩阵。

模型约束目标函数φ2(m)可表示为式(7)。

φ2(m)=‖Wmm‖2

(7)

其中：Wm为模型数据加权矩阵。

2.2 约束模型的构建

Wm作为模型数据加权矩阵，可以分为最小构造模型、最平坦模型和最光滑模型，三种矩阵模型如下：

为了验证不同约束模型对反演结果的影响，分别用三种约束模型对H型和K型地电模型进行反演，初始模型均为100 Ω·m的均匀半空间。得到最终结果见图7、图8。

由图7、图8可以看出，无论是中间层为低阻的H型模型或中间层为高阻的K型模型，采用不同约束模型得到的反演结果都能大致反应出模型的真实值。然而针对中间层为低阻的H型模型，采用最小构造模型约束的反演结果更精确。针对中间层为高阻的K型模型，采用最平坦模型约束得到的反演结果更为精确，在实际应用中需要根据不同的目标层选择合适的模型约束。

2.3 正则化因子的选取

正则化因子λ采用陈小斌[14]提出的CMD方案：

(8)

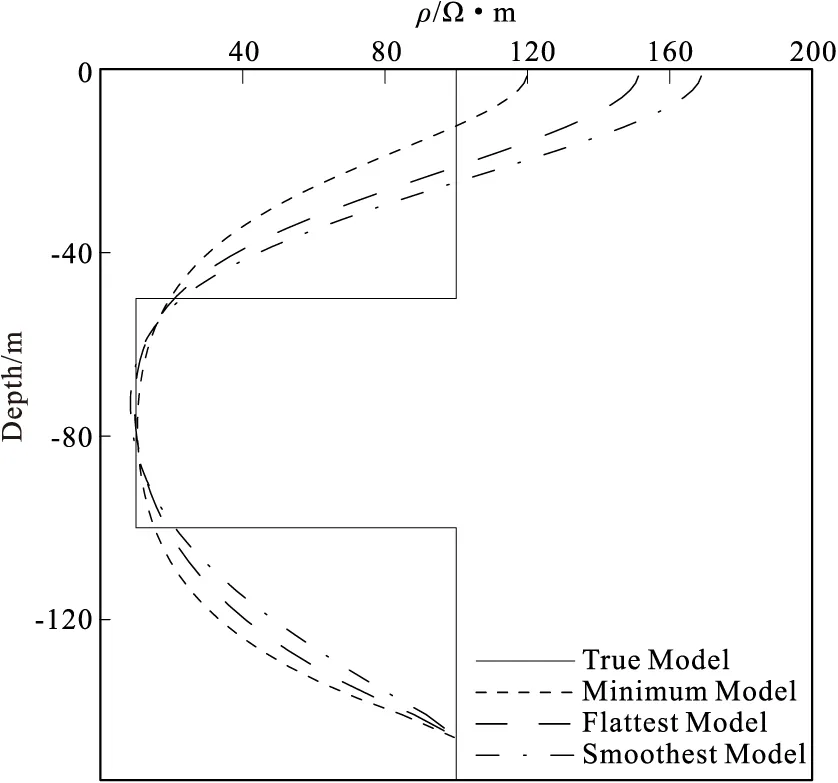
图7 不同约束模型下H型模型反演结果Fig.7 H model inversion results under different constraint models

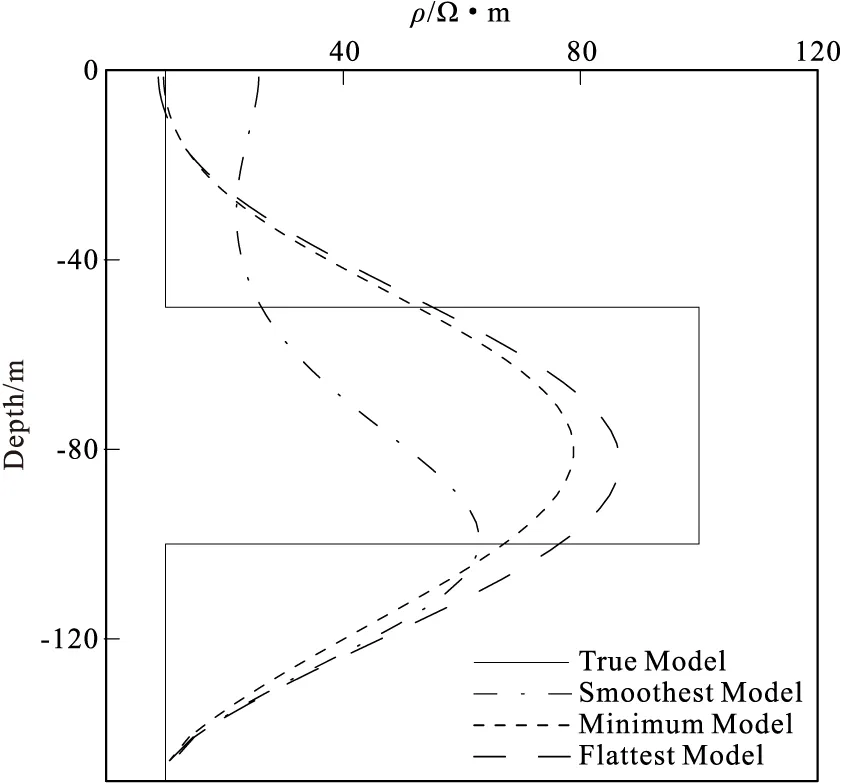
图8 不同约束模型下K型模型反演结果Fig.8 K model inversion results under different constraint models

采用这种方案，能同时满足观测数据目标函数和模型约束目标函数的需求，且不需要设置正则化因子的初值，对比常用的正则化方法，减少了计算量并提高了效率。

2.4 模型修正量及终止条件

根据总目标函数的极小化原则，可得到反演方程为式(9)。

(9)

其中：Δm为待求的模型修正向量；Jk为当前模型的雅克比矩阵。求解可得模型参数修正量为式(10)。

m=m0+Δm

(10)

反演的终止条件由相对拟合误差(RFE)进行判断，RFE定义为式(11)。

(11)

当反演拟合差小于RFE或者达到给定的迭代次数的时候反演迭代结束，从而得到最佳的反演模型。

2.5 反演模拟计算

为了验证反演程序的准确性，这里以两层D型地电模型，三层H型地电模型和四层HK型模型为例进行了最小构造模型约束下的自适应正则化反演计算。

设置发射电流为20 A，线源长度为1 000 m，接收点坐标为(0，200，50)。在时间为0.01 ms～10 ms内等对数间隔取32个采样点，设定RFE=1.0×10-5，迭代次数为10次，取拟合差最小的数据作为最终反演结果，初始模型为均匀半空间模型。反演模型参数如表1所示。

模型反演所得结果如图9、图10、图11所示。

从图9～图11中可以看出，反演结果曲线与设定模型拟合程度较好，验证了反演方法的有效性。然而通过对比可以发现，模型的高阻部分拟合程度较差，在H模型的起始高阻部分，出现了反演结果的电阻率值较实际模型电阻率略高的现象，在HK型模型的中间高阻层出现了反演结果比实际模型的电阻率值略低的现象。但是在模型的低阻部分，反演结果与模型拟合情况较好。说明该反演方法对于低阻层的识别性要高于高阻层，对于低阻层的反映值比较真实。

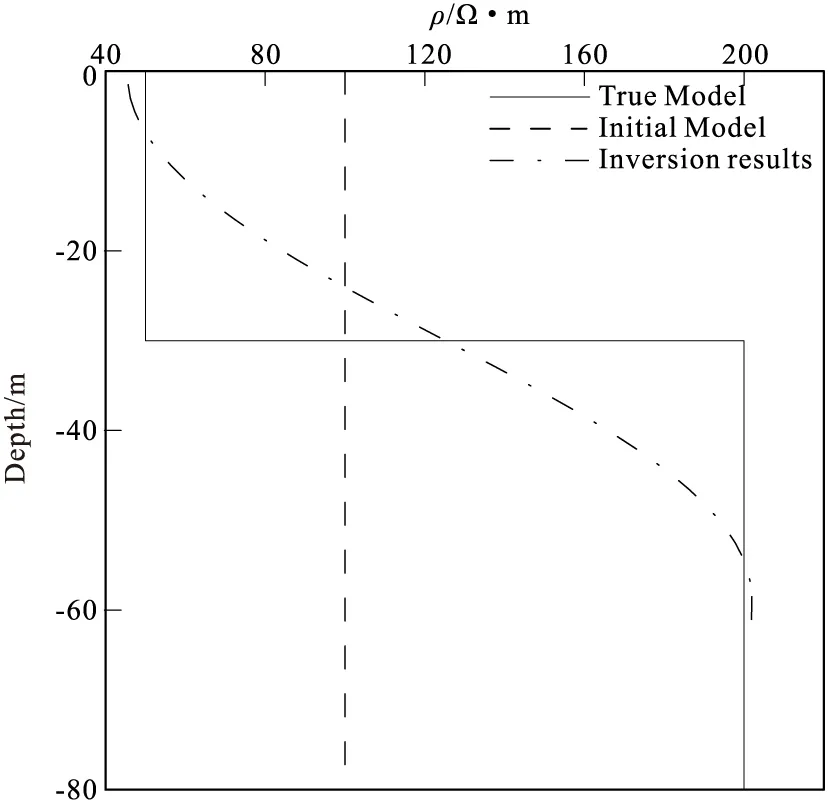
图9 D型模型反演结果图Fig.9 D model inversion results

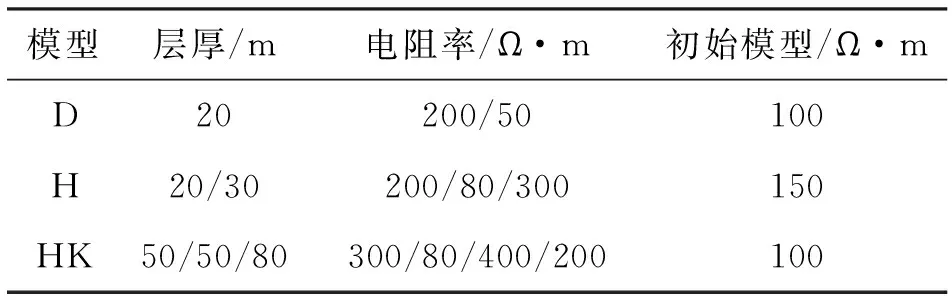
表1 模型参数Tab.1 Model parameters

图10 H型模型反演结果图Fig.10 H model inversion results

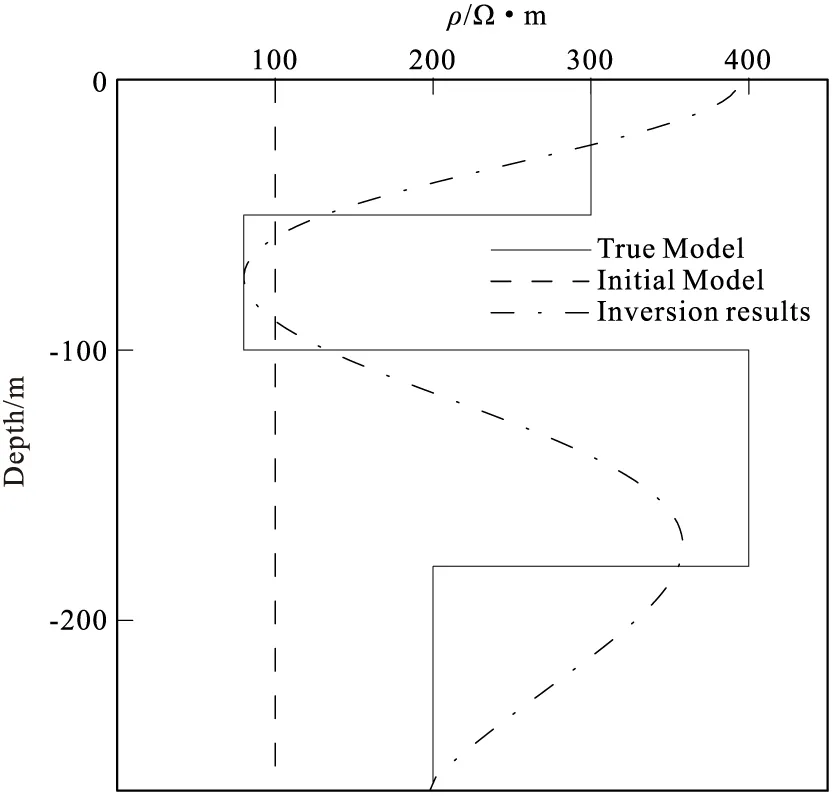
图11 HK型模型反演结果Fig.11 HK model inversion results

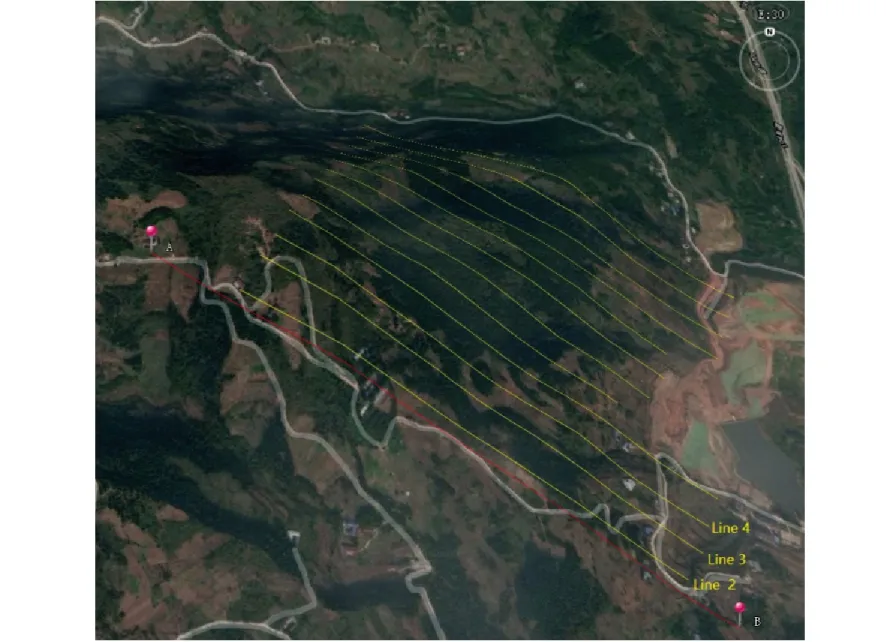
图12 测线布置三维地貌图Fig.12 A three-dimensional geomorphologic map of line layout

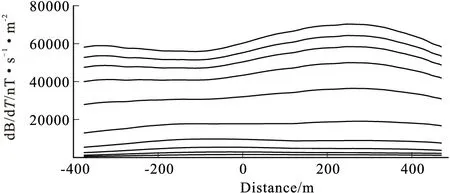
图13 测线2电磁响应曲线Fig.13 Electromagnetic response curve of Line2

3 应用实例

3.1 工区概况及测线布置

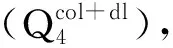
本次地空瞬变电磁测线布置如图12所示，从西北到东南海拔逐渐降低。其中红色线条表示线源布置，长度为1 100 m，黄色线条为测线布置，共计12条测线。测线长度因高压线影响，最长测线长度为800 m，最短测线为600 m，每条测线间距为50 m，测线与线源相互平行。

系统由发射系统和接收系统两部分组成。本次施工中发射系统采用TXU-30发射电流大小为20 A的双极方波。采用搭载接收机和感应线圈的无人机在空中进行接收，感应线圈的有效面积为1 055 m2,飞行高度为50 m，以2.5 m/s的速度沿着测线连续观测测量。

3.2 反演结果及解释

采集到的原始数据经数据预处理后得到电磁响应剖面，从电磁响应剖面可以初步判定信号的强度和质量。以测线2为例可以看出信号的强度较高，满足反演要求(图13)。

由于该滑坡的地质结构中间层电阻较低，采用最小构造模型约束的正则化反演方法进行反演工作，得到测线2的反演结果和地质解释推断图(图14、图15)。

图14 测线2数据反演结果Fig.14 Inversion results of Line2 measured data

图15 测线2地质解释推断图Fig.15 Geological interpretation inference map of Line 2

图16 反演切片图Fig.16 Inversion section diagram

由图14可以看出，反演结果可以较好地反映出滑坡的地下电性结构。图14的左上部表层呈现出的电阻率值相对较高，推测是第四系高阻覆盖层，中间含水夹层呈现明显的相对低阻特征，再向下达到电阻率较高的以中厚层砂岩为主的基岩层。随着地势的降低，滑坡电阻率呈现上低下高的趋势，推测是滑坡发生后导致含水坡积物堆积，表层电阻率降低。将已知的地质信息结合反演结果得到地质解释推断图(图15)，从上到下依次为覆盖层、强风化界线、含水层和基岩层。

将测线2、测线3、测线4联合做反演切片得到图16，可以看出测线的横向连续性较好，三条测线的电性结构大致相同，测线-300 m到0 m表层均反映出高阻特征；-300 m到0 m中间目标层均呈现低阻特征；0 m到400 m表层为表现出低阻的滑坡体堆积物；-300 m到400 m整体下层是呈现高阻的砂岩层。该结果与已有的地质资料吻合度较好，验证了地空瞬变电磁探测方法的有效性。

从图16可以得知，在滑坡区域使用地空瞬变电磁法来进行滑坡内部结构的探测，为滑坡区域提供内部电性构造，对于滑坡的治理有一定的积极意义。

4 结论

1)正演计算时利用Hankel变换、Gauss积分和频-时转换，得出了长导线源在层状介质中的时间域响应公式，并通过对比解析解和数值解的吻合程度，验证了正演程序的准确性。

2)通过对正则化自适应反演公式的推导，分析了不同约束模型对反演结果的影响，针对不同地质目标要选择合适的约束模型。经理论反演可得该方法对高阻层的反映有些偏差，对低阻层的反映较精确的特点。

3)通过对滑坡实测数据的反演研究可以发现，该方法可以较为准确地反映工区的地下电阻率分布，为进一步的解释工作提供了材料，为地空瞬变电磁系统的推广提供借鉴。

致谢

感谢审稿专家对本文的审阅及所提宝贵的修改意见，感谢物探化探计算技术期刊以及编辑部的审稿、收录等帮助。