基于BP神经网络的海啸爬坡高度预测

周哲儒, 苏 波

(江苏大学 土木工程与力学学院, 江苏 镇江 212000)

海啸是人类近海生产作业的一大威胁,它通常是由于板块运动和巨物的突然下坠引起,巨浪冲击至岸边后不仅会摧毁沿海的堤岸、码头、建筑等,还会席卷人类,对人民生命和财产安全造成严重威胁,因此,对近岸海浪爬坡高度的研究预测,对海岸工程,减少财产损失及人员伤亡具有重要意义[1]。

在研究海啸最高爬坡高度时,通常将海啸波简化为孤立波计算,近年来,国内外的学者对孤立波的最大爬坡高度进行了较多的研究,主要以理论、数值模拟计算、试验研究方面为主。理论方面,Madsen等[2]理论研究了海啸波的波列,包括孤立波和N波的爬高和回落的解析解。试验研究方面,Hsiao等[3]在1∶60的平摊海面上进行了破碎孤立波演化的实验,提出了1个简单的可用于预测(1∶15～1∶60)均匀海滩上破碎孤立波的最大爬升高度。Nimish等[4]采用1∶12的斜坡,研究了在不同波峰间距下,等高双孤立波的爬高互相影响。荣一毅等[5]首次在1/10的斜坡上进行等三孤立波的爬高实验,分析了孤立波爬高放大系数随波峰间距变化的规律。数值模拟方面,Tsung[6]利用Boussinesq模型对孤立波的爬坡和漫顶进行了数值模拟。

近年来,神经网络快速发展,它具有良好的自适应学习能力和非线性映射能力,常用于处理物理机制、因果关系复杂的非线性问题。Mandl等[7]采用递归神经网络,以印西海岸实测海浪为模型,预测结果的相关系数较高。Günaydin等[8]采用前馈反馈传播(FFBP)和广义回归神经网络(GRNN)2种人工神经网络方法预测海啸上升高度,预测效果良好。

本文利用OpenFOAM对孤立波爬坡运动进行数值模拟,获取相关爬高运动参数,并在此基础上使用BP神经网络实现了对孤立波爬坡高度的预测,输出结果具有较好的精度。

1 模型建立与分析

通过OpenFOAM软件进行模拟仿真,建立数值波浪水槽,对孤立波爬高进行数值模拟。建立如图1所示的计算模型,图中波高为H0,静水面深度h0,斜坡角度为β,波浪的最大爬坡高度为R,分别建立静水深h0为1.2 m、2.2 m、2.9 m 3种工况,模拟3种不同静水深度情况下孤立波运动情况以获取孤立波爬坡高度R。

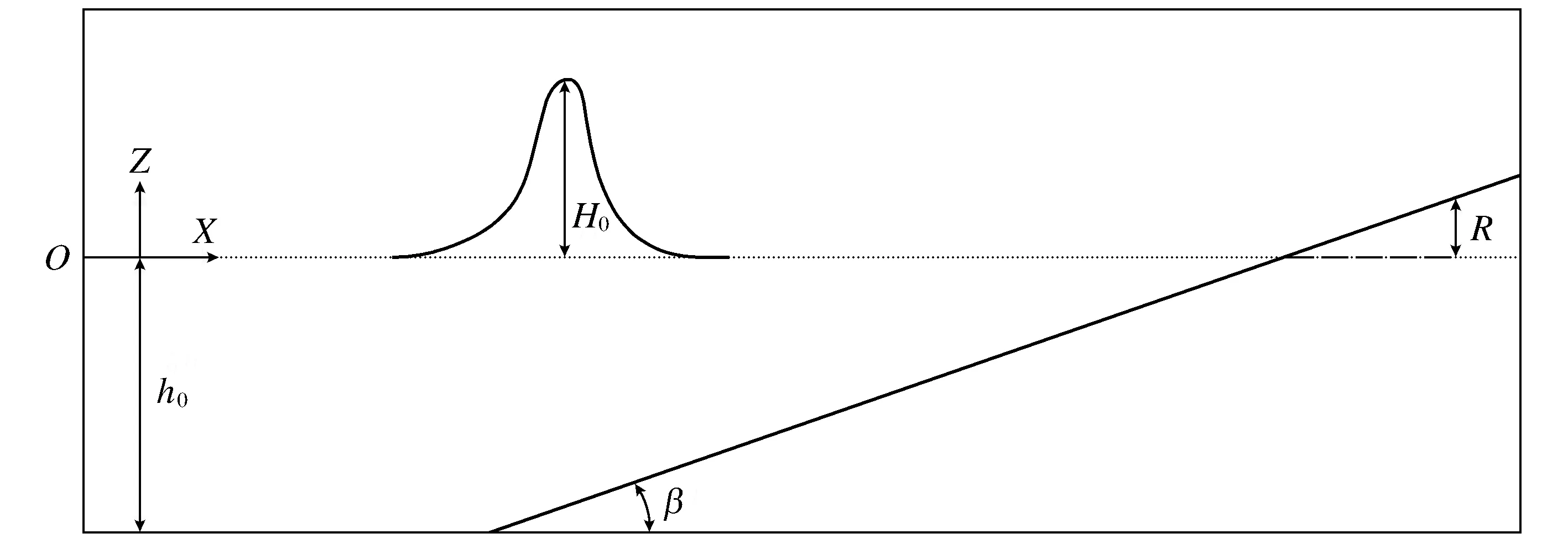
图1 数值计算模型示意图Fig.1 Numerical calculation model diagram

图2为通过OpenFOAM所建立的二维数值波浪水槽示意图,其中岸滩为定床,不因波浪的影响而改变,且孤立波运动至岸边直至破碎,静水深计算高度始终为h0不变。

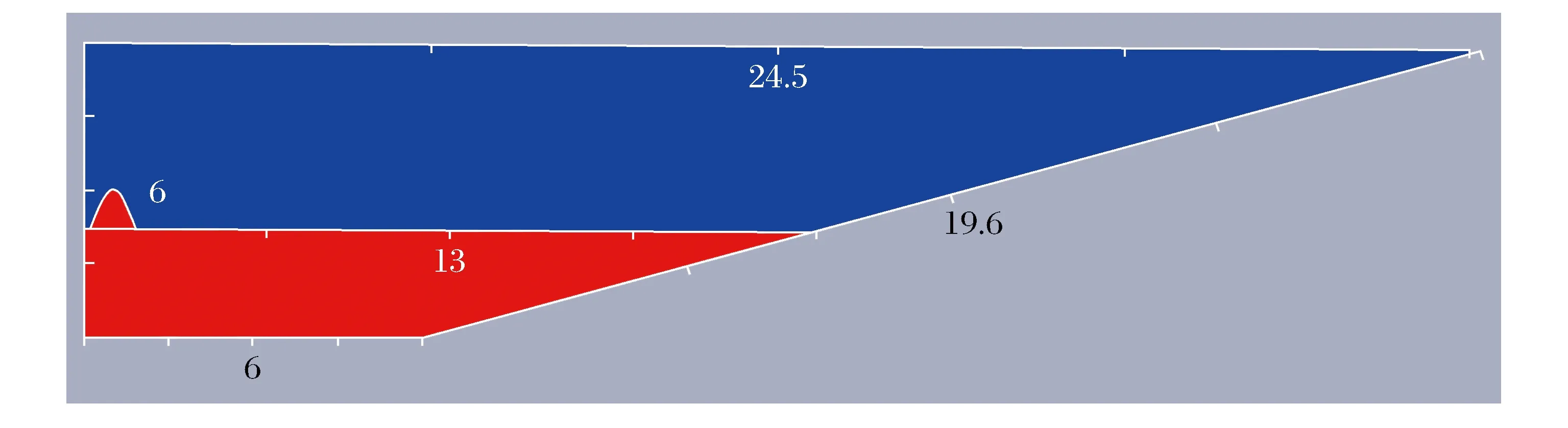
图2 二维数值波浪水槽示意图Fig.2 Schematic diagram of a two-dimensional numerical wave flume

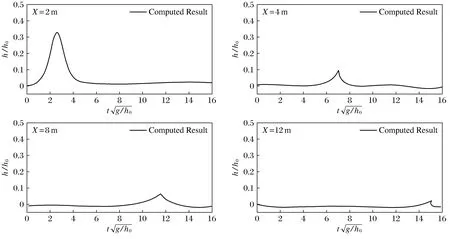
图3 不同位置处波面时程变化曲线(h0=2.2 m)Fig.3 Time history curve of wave surface at different positions(h0=2.2 m)

初始运动状态下,波高最大,随着不断运动,势能消耗,波高逐渐变小,待运动至岸边时,孤立波破碎,波高几乎为0,由此可见该模型较好地模拟了孤立波的实际运动状态。为了进一步验证模拟结果与理论值的差异,这里引入Synolakis孤立波最大爬高公式进行数值验证,公式如下:

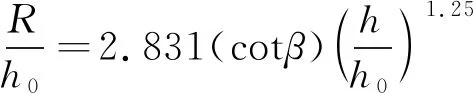
(1)

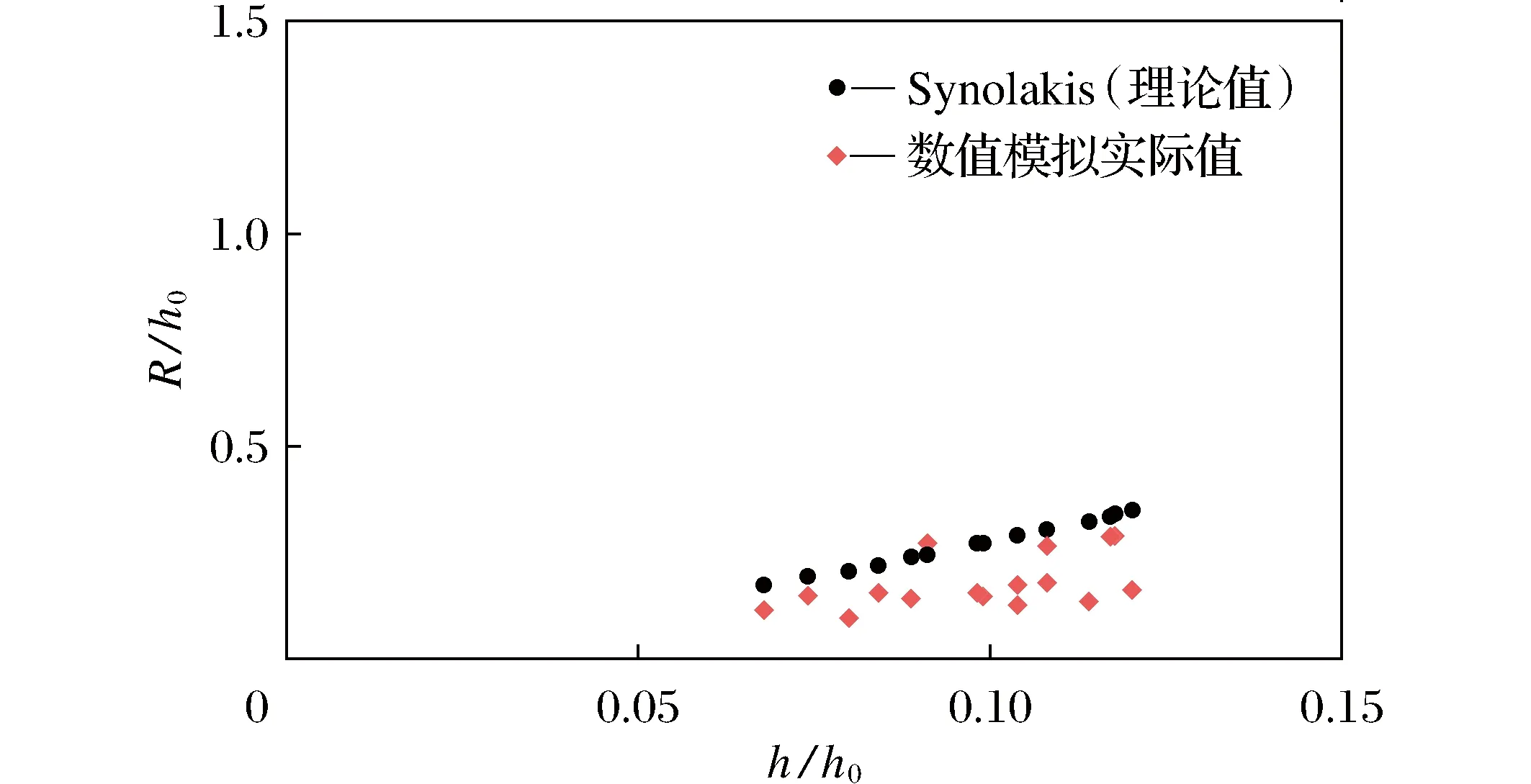
图4 Synolakis理论相对爬高与数值模拟结果对比Fig.4 Synolakis theory relative climb and comparison of numerical simulation results

式中:R/h0为相对波高;h/h0为相对爬高;β为坡脚。

绘制出数值模拟真实值与通过经验公式所得理论值的比较图,如图4所示。 从图中可以看出, 理论值分布大致呈一条直线,数值模拟的实际值分布较为离散, 与理论值相比,存在一定的差距。 但从数值上分析来看, 任意一组理论值与数值模拟实际值误差均小于0.2, 误差最大为0.186, 最小为0.028, 平均相对误差约为17%, 总体看来,模拟数据具有一定的精度, 较好地反映了孤立波的实际爬高情况。

2 BP神经网络孤立波爬高预测模型

BP(back propagation)神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,它具有较强的非线性映射能力和柔性网络结构[10],能够通过分析大量数据来获取其内在联系,从而解决一些非线性问题。一个完整的神经网络主要由输入层、输出层和一个或若干个隐藏层组成,通过不断优化各层之间的连接权值、阈值,最终达到最好的拟合结果。有关BP神经网络的网络结构、算法原理、流程可详见文献[11-12]。

2.1 建立模型

对孤立波的爬高进行预测,首先确定孤立波爬高的影响因素,其次获取大量的样本数据。

2.1.1 孤立波爬高影响因素

2.1.2 样本数据获取

本文共选取70组样本,除了数值模拟的16组样本外,另外54组来源于文献[3],将它们打乱后随机选取50组作为预测样本,剩余20组作为测试样本,样本数据如表1所示。

表1 实测与模拟样本数据Table 1 Measured and simulated sample data

2.2 网络参数设置

输入层、隐藏层、输出层节点数分别为3、3、1，其中隐藏层为2层,学习率为0.15,最大学习次数10 000次,激活函数为对数型Sigmoid函数[14]。

3 结果分析

训练结果如图5～图7所示。由图5可知,在训练了10 000次左右,可以看出误差最终介于(0,0.02)之间,训练样本结果实现了有效收敛。图6绘制了20组预测样本真实值与预测输出值的比较,图中可以看出,BP神经网络对数据的预测情况较为良好,预测样本的实际值与预测值走势较为相同。从图7可以更直观的看出,样本数据分布在直线y=x上,部分在直线两侧,拟合性较好。计算真实值与预测值的相关系数R=0.941 8,为高相关性,因此,本文提出的基于BP神经网络的爬高预测模型具有一定的估测能力。但从图6、图7可看出,有几组样本偏离值较大,输出结果和真实值对比存在显著误差,主要因为以下几个原因:

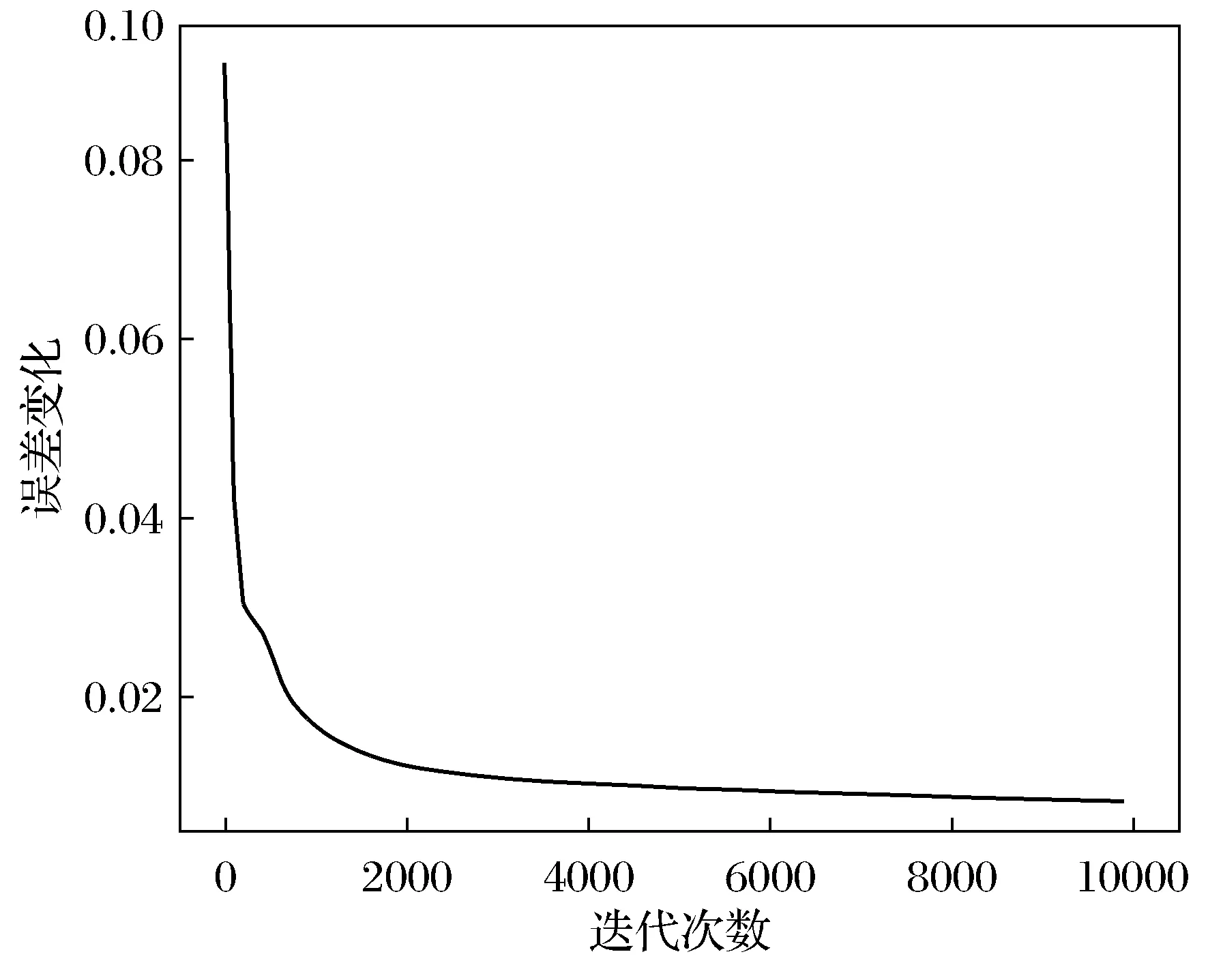
图5 迭代训练图Fig.5 Iterative training diagram predicted

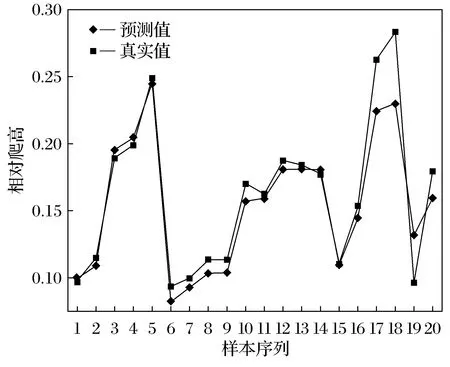
图6 预测样本实际值与预测值比较Fig.6 Comparison of predicted value and actual value

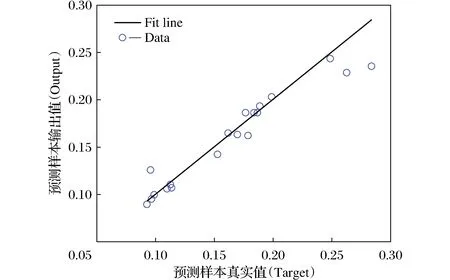
图7 预测样本回归图Fig.7 Regression diagram of predict samples

1) 样本容量不足。神经网络对样本数量具有一定的要求,样本不足可能导致训练得到的模型不具有一般适用性,部分样本对模型变现较为不敏感,得不到理想输出结果。

2) 网络参数学习率的选取。学习率的过大会造成误差不递归,不具规律性,过小则会导致训练次数过多,误差ei不下降。所以学习率选取也会导致最终训练模型不具有一般适应性,即误差仍然存在。

4 结 论

BP神经网络是一种按照误差逆向传播算法训练的神经网络,它用于处理一些非线性数据类型具有巨大的优势,本文借助BP神经网络对孤立波爬高进行了预测,这对我国部分沿海地区评估海啸风险、防灾减灾及近岸基础设施的建设提供了参考。值得说明的是,本文的模型输入因子仅包含静水深、坡脚等因素,实际情况下要复杂的多,还有可能和海面上风速、海底底面的摩擦系数等因素有关[15],因此,在输入因子选取方面可以不断地探索以求获得更完善的结果。