可见光与红外图像组K-SVD融合方法

王志社，姜晓林，武圆圆，王君尧

可见光与红外图像组K-SVD融合方法

王志社，姜晓林，武圆圆，王君尧

（太原科技大学 应用科学学院，山西 太原 030024）

传统稀疏表示融合方法，以图像块进行字典训练和稀疏分解，由于没有考虑图像块之间的内在联系，易造成字典原子表征图像特征能力不足、稀疏系数不准确，导致图像融合效果不好。为此，本文提出可见光与红外图像组K-SVD（K-means singular value decomposition）融合方法，利用图像的非局部相似性，将相似图像块构造成图像结构组矩阵，通过组K-SVD进行字典训练和稀疏分解，可以有效提高字典原子的表征能力及稀疏系数的准确性。实验结果表明，该方法在主观和客观评价上都优于传统稀疏融合方法。

图像融合；非局部相似性；结构组矩阵；组K-SVD

0 引言

红外成像技术通过接收目标的红外辐射，将肉眼不可见的红外辐射能量转化为电信号进行成像，可以探测到隐藏目标或伪装目标，具有很好的抗干扰能力，可以全天时全天候工作；可见光成像技术通过捕捉物体的反射光进行成像，可以很好地获取物体的细节信息、颜色信息和纹理特征[1-2]，但易受天气、光照的影响。因此，可见光与红外图像具有较强的互补特性，只有将这两类图像信息进行融合，综合两类图像的互补信息，才能够有效提高成像系统的性能[3-4]。

目前，可见光与红外图像融合方法大致可以分为多尺度变换融合[5-6]、稀疏表示融合[7-11]、混合模型融合[12-14]、拟态融合[15]、深度学习融合[16-17]等。多尺度变换融合方法采用尺度变换数学模型描述图像特征，采用相应的融合规则进行合并，得到最终的融合图像。由于尺度变换数学模型往往对某一类图像特征敏感，易造成融合图像信息缺失。稀疏表示融合方法利用字典原子表征图像特征，通过合并稀疏系数重构得到最终的融合图像。Yang等[9]首次提出基于稀疏表示的图像融合算法，随后，Yu等[10]提出联合稀疏融合方法，Liu等[11]提出自适应稀疏融合方法，提高了稀疏融合的效果。混合模型融合方法采用多种算法进行嵌入、组合，如多尺度稀疏融合[12]、多尺度嵌入融合[13-14]等，混合模型融合方法在一定程度上克服了单一融合方法的局限性。拟态融合方法[15]是利用可见光与红外图像的差异特征，驱动选择相应的融合算法，为图像融合方法提供了新的研究思路。深度学习融合方法利用神经网络自主学习图像特征，获得了较好的融合效果[16-17]。

稀疏表示在过完备字典上对图像信号进行表示，可以有效表征图像特征，是目前图像融合的热点之一。但传统稀疏表示图像融合方法将图像分割成重叠的块，字典训练及稀疏分解过程均以图像块为单位进行，块与块之间是相互独立的，造成图像特征不能被准确提取，融合效果较差[18]。图像中的局部位置和非局部位置存在相似结构，这种特征被称为非局部相似性，通过非局部相似性可以建立图像相似块之间的联系。非局部相似性在图像去噪、图像去模糊等方面取得较好效果[19-20]。

可见光与红外图像融合就是要将两类图像的显著特征进行有效合并，而实际上，图像中的显著特征不仅与局部结构有关，还与图像非局部结构有关。从两类图像的成像机理和成像特点可以看出，可见光图像具有丰富的结构信息，图像块反映了局部的几何结构，相似的结构在图像不同位置重复出现，具有非局部结构相似性。而红外图像中，绝大多数为背景区域，其灰度变化缓慢，背景区域的图像块之间存在较强相关性，也具有明显的非局部结构相似性。为了直观显示，如图1所示，通过计算图像结构块的相似性，在可见光与红外图像分别自动选取了7个图像相似块，并进行局部放大，可以看出，图像相似块具有明显的非局部相似性，这也说明，可见光与红外图像的局部位置及非局部位置上均存在结构相似的图像块。因此，通过建立图像局部结构与非局部结构的内在联系，将相似的图像块构建成图像结构组，以结构组代替传统的图像块，利用结构组的重复结构和冗余信息，通过对结构组进行字典学习和稀疏分解，可以使字典原子和稀疏系数更有效地描述图像显著特征，从而有效解决传统稀疏表示融合方法存在的问题。

本文针对传统稀疏表示融合方法字典表征能力不足，稀疏系数不准确的问题，通过非局部相似性建立相似图像块之间的联系，以欧氏距离为度量准则，依据图像的非局部相似性特征将相似图像块采用向量化、矩阵化的方式构建为结构组矩阵，在此基础上，构建组K-SVD训练模型，以结构组代替传统图像块，优化结构组字典学习和稀疏分解问题，将源图像的相似结构特征与融合过程充分结合。该方法建立了图像块之间的内在联系，以结构组矩阵为单位进行字典训练和稀疏分解，增强了字典原子的表征能力和稀疏系数的准确性，提高了图像的融合性能。

图1 可见光与红外图像非局部相似性示意图

1 模型构建

1.1 结构组矩阵构造

结构组矩阵构造基于图像的非局部相似性特征，首先采用滑动窗将源图分割成大小相同的图像块，然后根据相似性度量准则，从图像的确定邻域内提取相似块，对相似块采取向量化、矩阵化的方式构建成结构组矩阵，用于字典训练和融合过程，具体过程如图2所示。

1）图像块提取

假设源图像1、2的大小均为×像素，采用滑动窗，滑动步长为1像素，按照图中所示的轨迹，自左向右、自上而下进行滑动。分别将源图像分解为大小为×的(－＋1)·(－＋1)个图像块。

2）结构组构建

在×的邻域内，以欧式距离作为度量准侧，计算每一个初始图像块x最相似的个图像块。将初始图像块x与个相似图像块构成一个结构组G，这样每个结构组中共有＋1个图像块。对于×的输入源图像，共有(－＋1)·(－＋1)个初始块，则可以构建(－＋1)·(－＋1)个结构组。

3）图像块向量化

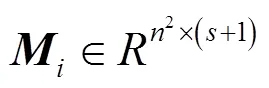
图2 相似结构组矩阵示意图

1.2 组K-SVD字典训练模型

假设信号∈R，字典∈R×，当大于时，称字典为冗余字典。信号可以表示为＝或者≈。∈R为稀疏表示系数，中的多数元素为0，只有少数元素不为0，称是稀疏的，可以在字典上稀疏表示。因此，稀疏表示就是将信号表示为一个冗余字典中少数原子的线性组合。由于实际应用中存在噪声，当考虑噪声时，信号在字典上的稀疏表示求解可以表示为：

对于结构组矩阵，在对应的字典上的稀疏表示优化问题可以表示为如下的形式：

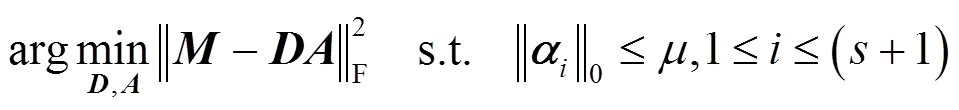
在字典学习中，字典更新阶段是在系数矩阵不变的情况下，对字典进行更新。可以表示为下面的优化问题：

上式中的优化问题有一个封闭解，可以通过单独对中的每一列求解，并且在求解过程中，只更新每一列的非零项，值为零的项保持不变，这样的优化问题可以表示为：

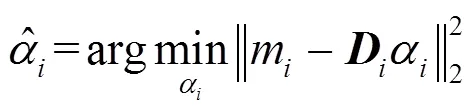
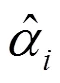
上述迭代算法先更新字典，后更新系数矩阵，可以得到式(3)优化问题的近似解。组K-SVD算法对迭代更新过程进行了改进，结构组矩阵在字典上的稀疏编码优化问题可以表示为：

2 融合方法

可见光与红外图像组K-SVD融合方法如图3所示，具体步骤如下：

图3 融合方法总体框架

1）图像块提取：对于大小为×的输入源图像1、2，采用滑动窗技术，滑动步长为1像素，按照从左到右、自上而下的轨迹遍历整幅图像。设图像块大小为×，则可以分别提取源图像1、2的(－n＋1)·(－＋1)个图像块。

2）结构组矩阵构建：对源图像1，在×的邻域内，以欧式距离为度量准则，计算出初始图像块的最相似的个图像块，并进行块向量化、结构组矩阵化处理，得到相应的结构组矩阵；对源图像2，每个初始块对应的相似块与1相同。

3）训练样本选取及字典学习：从源图像中随机选出个初始块作为训练样本，采用组K-SVD字典训练方法求解源图像对应的字典。

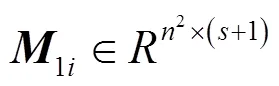
5）稀疏系数融合：1i()、2i()，＝1, 2, …,＋1为系数向量，分别为稀疏系数矩阵1、2的第列。对应的稀疏系数向量采用绝对值取大的规则进行融合：

最终得到融合系数矩阵Fi。

6）图像重构：将得到的系数矩阵Fi与字典重构得到融合结构组矩阵，对结构组矩阵进行逆变换得到融合的图像块，之后将每一个图像块放回到对应的位置，相同位置像素进行均值化，得到最终的融合图像。

3 实验结果及分析

3.1 设定

为了评价组K-SVD融合性能，实验采用4组可见光与红外图像，分别为“UNcape”、“Kaptein”、“Dune”和“Road”。对比的融合方法采用3种传统的稀疏融合方法，分别为稀疏表示融合方法（Sparse Representation, SR）[9]、联合稀疏融合方法（Joint Sparse Representation, JSR）[10]和自适应稀疏融合方法（Adaptive Sparse Representation, ASR）[11]。评价指标采用0[21]、w[22]、e[22]和ab/f[23]四个评价指标。0从图像的亮度、对比度和结构失真度来衡量融合图像的退化程度，w描述源图像的显著信息转移到融合图像的合并程度，而e和ab/f主要描述源图像到融合图像的边缘信息融合程度。评价指标数值越大，说明融合效果越好。

组K-SVD融合方法参数设定如下：①结构组构造模型参数，图像块大小为8×8，滑动窗大小为40×40，滑动步长为1像素。②结构组稀疏模型参数，训练样本图像块数量为10000，相似图像块个数设定为19，字典大小为64×256，字典原子稀疏度为5。

3.2 结果分析

4组可见光与红外图像的融合结果如图4～图7所示，其中，(a)和(b)分别表示可见光与红外图像，(c)、(d)、(e)分别是稀疏表示融合方法、自适应稀疏融合方法和联合稀疏融合方法得到的融合图像，(f)是本文方法得到的融合图像。

图4为“Nato_camp”的融合实验结果。从图4(a)和(b)可以看出，红外图像行人目标位置清晰，背景信息（如树木、道路和房屋等）细节不清楚，信息丢失较为严重；而可见光图像中，道路、树木和房屋等背景信息清晰，但行人目标缺失，可以看出这两类图像具有很大的互补性。图4(c)是SR融合图像，可以看出，融合图像的边缘信息较为模糊，纹理信息缺失严重；图4(d)是ASR融合图像，融合图像较好保留了两类图像的主要互补信息，但依然存在图像边缘信息模糊，存在一定的伪影现象；图4(e)是JSR融合图像，行人目标清晰，对比度较高，但融合图像存在过增强现象，背景信息缺失严重。图4(f)是本文方法的融合图像，从结果可以看出，融合图像行人目标位置、轮廓信息清楚，背景信息如树木、房屋、道路等保留较好，图像整体视觉效果好于传统稀疏融合方法。

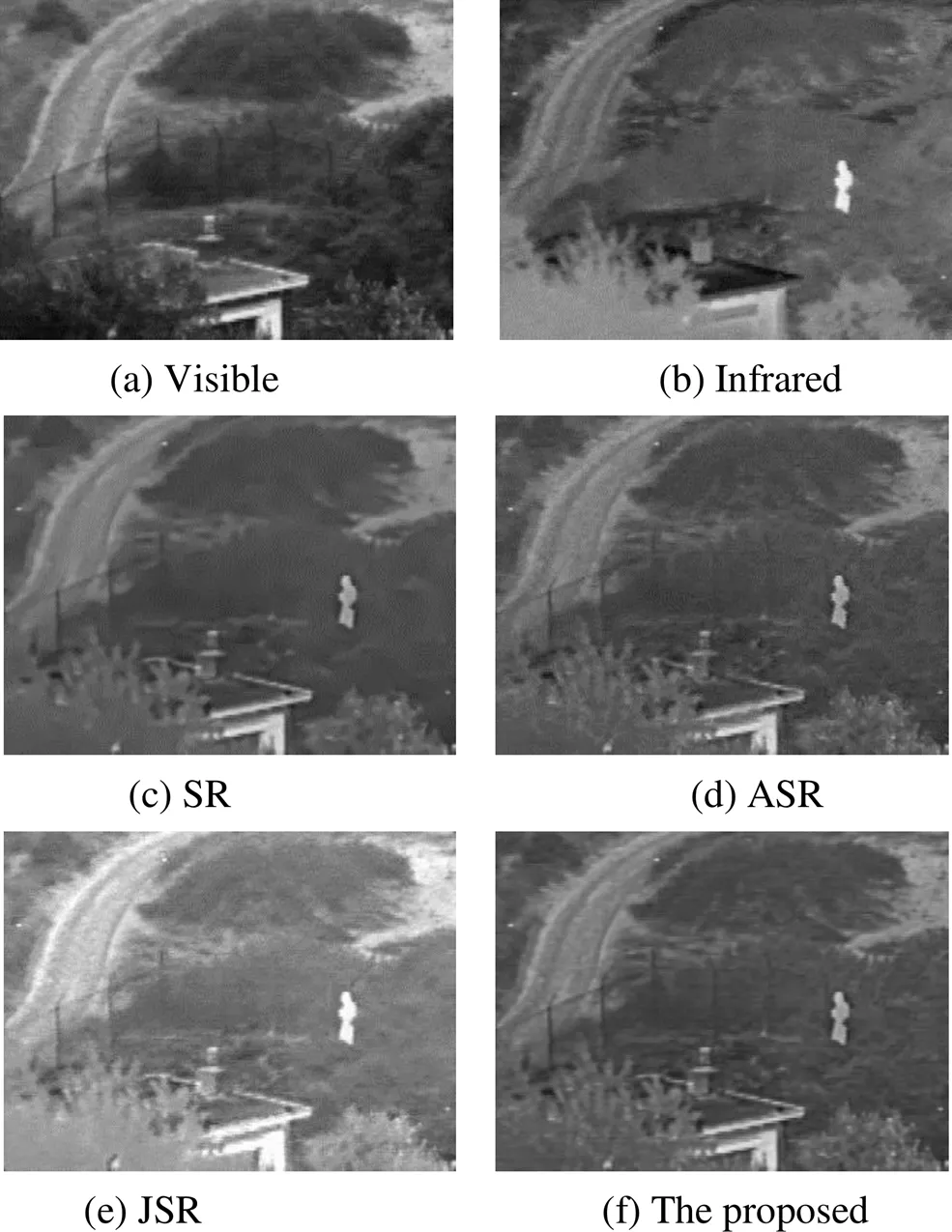
图4 “Nato_camp”图像融合实验结果

图5为“Kaptein”的融合实验结果。图5(a)和(b)分别是可见光和红外图像，图5(c)、(d)和(e)分别是SR融合图像、ASR融合图像和JSR融合图像。从结果可以看出，SR融合图像虽然保留了红外图像的目标信息，但图像背景细节信息丢失严重，例如地面、树木等；ASR融合图像视觉效果好于SR融合图像，行人目标、背景信息较为清楚，但边缘信息较为模糊；JSR融合图像行人目标的对比度较高，但融合图像过增强现象严重，如树木、门窗的边缘细节信息丢失。图5(f)是本文方法的融合结果，可以看出，融合图像包含了两类图像的主要互补信息，行人、地面、树木等细节信息清楚，视觉效果较好。

图6和图7分别为“Duine”和“Road”的融合实验结果。从实验结果来看，SR和ASR的融合效果相对较差，JSR融合图像虽然对比度较高，但细节信息丢失严重，本文方法的融合图像视觉效果较好，图像中的细节信息及边缘轮廓信息保留完整。从主观视觉来看，4组实验结果评价结果一致。

图5 “Kaptein”图像融合实验结果

图7 “Road”图像融合实验结果

4组可见光与红外图像融合结果的客观评价指标如表1～表4所示，表5为客观评价指标的平均值。从结果来看，对于“Kaptein”图像，本文融合方法获得最好的融合效果；对于“Nato_camp”图像，本文的融合方法在评价指标w、e和ab/f获得最优的结果，0指标略低于ASR的结果；对于“Duine”和“Road”图像，本文的融合方法在评价指标w和e获得最优的结果，而指标0和ab/f低于ASR方法，这说明本文的融合方法在提取显著特征信息和边缘信息保留方面效果较好，总体来看，本文的融合方法优于传统的稀疏表示融合方法。

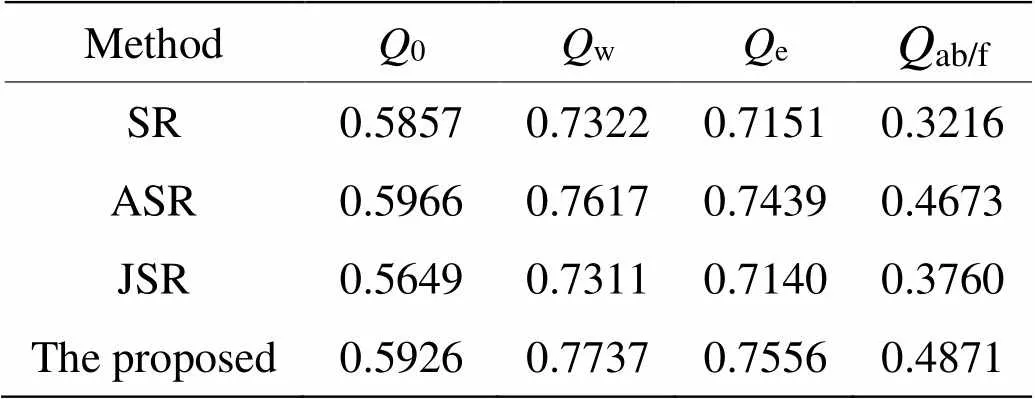
表1 “Nato_camp”图像融合客观评价指标

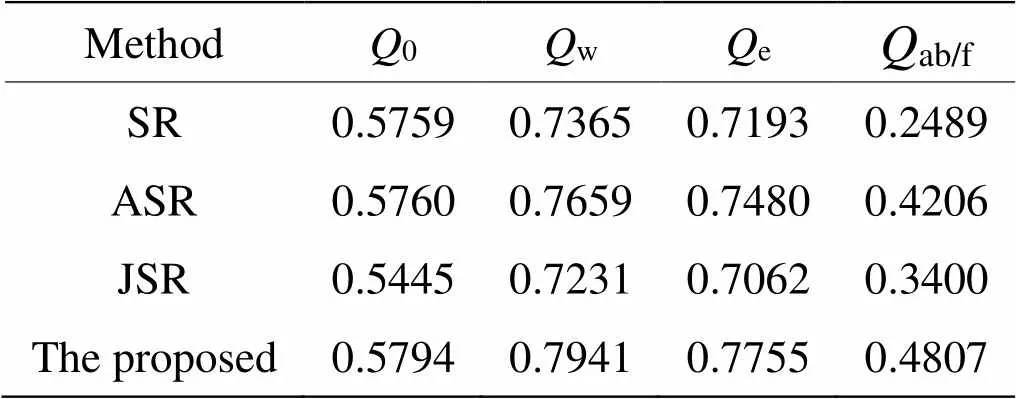
表2 “Kaptein”图像融合客观评价指标

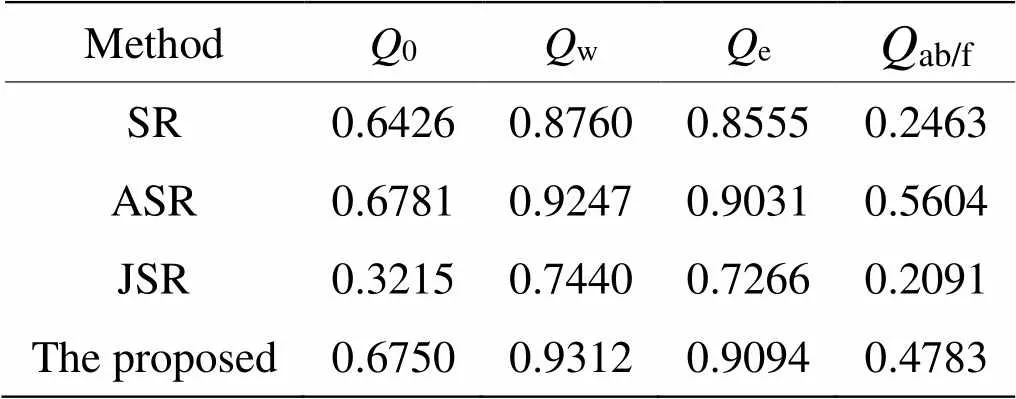
表3 “Duine”图像融合客观评价指标

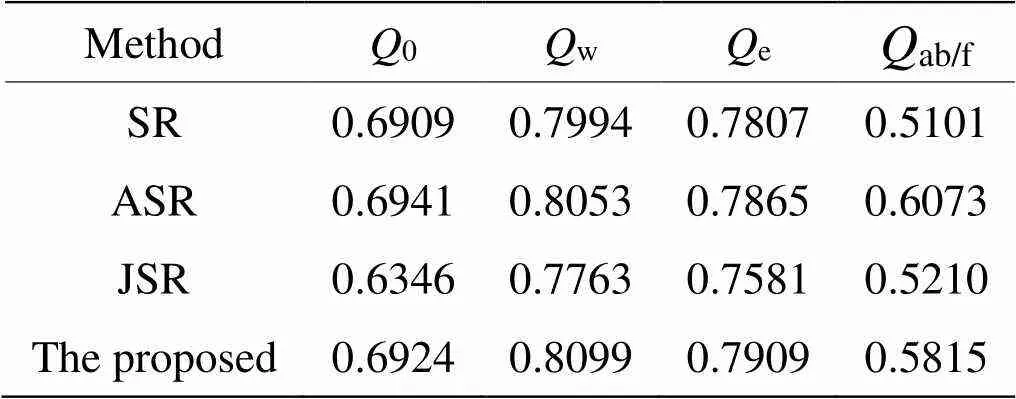
表4 “Road”图像融合客观评价指标

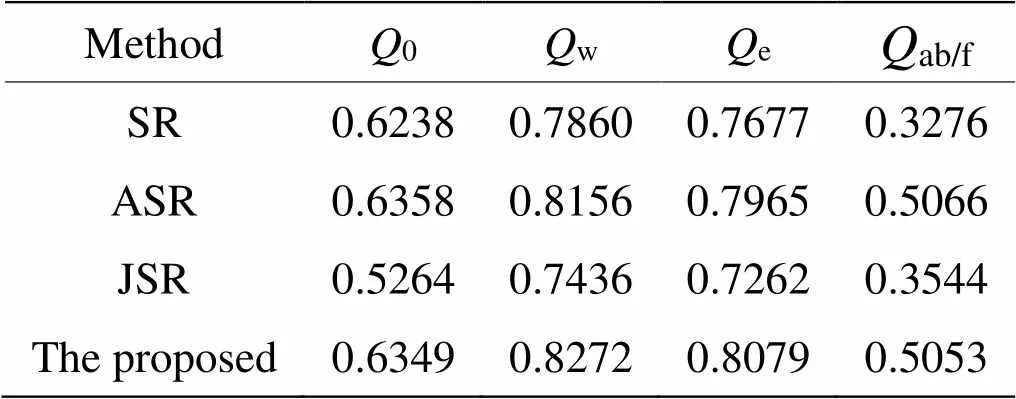
表5 不同融合方法评价指标的平均值

为了进一步对融合效果进行评价，采用两组名为“Nato_camp”和“Duine”的图像序列进行实验。“Nato_camp”图像序列为同一场景中32幅在时间上连续的图片，“Duine”图像序列为同一场景中23幅在时间上连续的图片。采用0、w、e和ab/f对融合效果进行评价。将得到的评价指标绘制为曲线图进行对比，具体的绘制方法为：分别将4种融合方法的0值绘制为曲线，并将这4条曲线整合到同一幅图像中；另外3种评价指标曲线图的绘制方法与0相同。

图8和图9分别为图像序列“Nato_camp”和“Duine”对应的曲线图。如图8所示，(a)、(b)、(c)、(d)分别为评价指标0、w、e和ab/f对应的曲线图。每幅图中，点状曲线对应SR方法的评价指标，圈型曲线对应ASR方法，块状曲线对应JSR方法，叉型曲线对应本文提出的方法，右下角为图像序列不同融合方法对应评价指标的平均值。通过两组分析曲线可知：在图8中本文方法的0值低于ASR方法，w、e和ab/f值均为最高；在图9中本文方法的0、w和e值略低于ASR方法，ab/f值为最高。

因此，通过对4组可见光与红外图像及两组图像序列进行融合实验，结合主观视觉效果和客观评价指标对实验结果判断，本文方法与另外3种方法相比，融合效果最好。

4 结语

本文提出了可见光与红外图像组K-SVD融合方法，利用图像非局部相似性，以欧式距离为度量准则，构建图像结构组矩阵，以结构组代替传统的图像块，在此基础上，研究了组K-SVD的稀疏分解模型，以结构组矩阵作为训练样本，构建学习字典，并进行组稀疏分解，采用绝对值取大的合并规则进行合并，得到最终的融合图像。实验结果表明，该方法可以有效提取图像的显著特征信息，减少边缘特征信息丢失，融合图像视觉效果较好，在主观和客观评价上，都优于传统的稀疏表示融合方法。

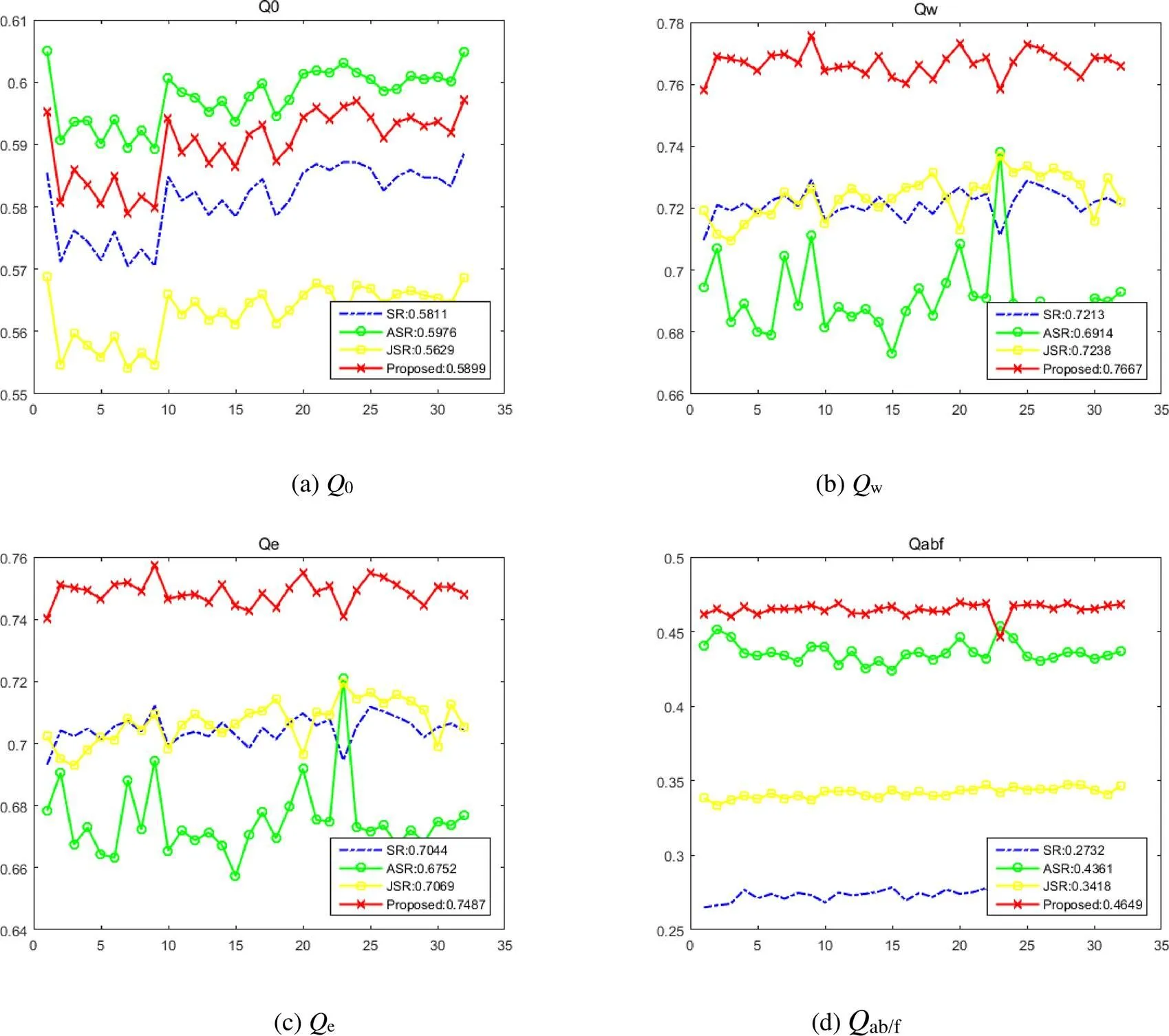
图8 图像序列“Nato_camp”的客观评价指标

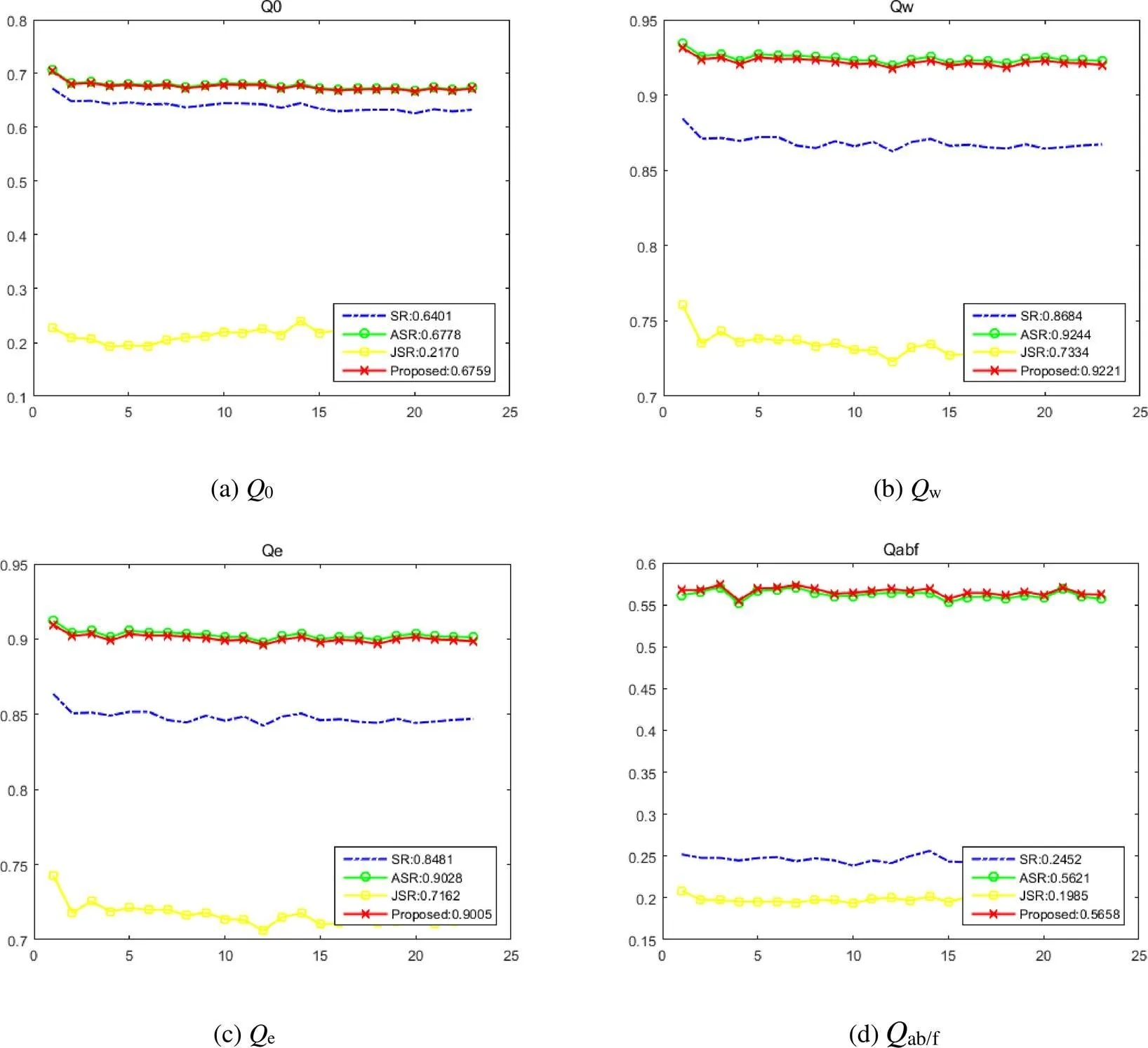
图9 图像序列“Duine”的客观评价指标

4 结语

本文提出了可见光与红外图像组K-SVD融合方法，利用图像非局部相似性，以欧式距离为度量准则，构建图像结构组矩阵，以结构组代替传统的图像块，在此基础上，研究了组K-SVD的稀疏分解模型，以结构组矩阵作为训练样本，构建学习字典，并进行组稀疏分解，采用绝对值取大的合并规则进行合并，得到最终的融合图像。实验结果表明，该方法可以有效提取图像的显著特征信息，减少边缘特征信息丢失，融合图像视觉效果较好，在主观和客观评价上，都优于传统的稀疏表示融合方法。

[1] MA J, MA Y, LI C. Infrared and visible image fusion methods and applications: A survey[J]., 2019, 45: 153-178.

[2] LI S, KANG X, FANG L, et al. Pixel-level image fusion: a survey of the state of the art[J]., 2017, 33: 100-112.

[3] Elguebaly T, Bouguila N. Finite asymmetric generalized Gaussian mixture models learning for infrared object detection[J]., 2013, 117(12): 1659-1671.

[4] LI H, DING W, CAO X, et al. Image registration and fusion of visible and infrared integrated camera for medium-altitude unmanned aerial vehicle remote sensing[J]., 2017, 9(5): 441.

[5] LI S, YANG B, HU J. Performance comparison of different multi- resolution transforms for image fusion[J]., 2011, 12(2): 74-84.

[6] FU Z, WANG X, XU J, et al. Infrared and visible images fusion based on RPCA and NSCT[J]., 2016, 77: 114-123.

[7] ZHANG Q, LIU Y, Blum R, et al. Sparse representation based multi-sensor image fusion for multi-focus and multi-modality images: a review[J]., 2018, 40: 57-75.

[8] ZHANG Z, XU Y, YANG J, et al. A survey of sparse representation: Algorithms and Applications [J]., 2015(3): 490-530.

[9] YANG B, LI S. Multifocus image fusion and restoration with sparse representation[J]., 2010, 59(4): 884-892.

[10] YU N, QIU T, BI F, et al. Image features extraction and fusion based on joint sparse representation[J]., 2011, 5(5): 1074-1082.

[11] LIU Y, WANG Z. Simultaneous image fusion and denoising with adaptive sparse representation[J]., 2014, 9(5): 347-357.

[12] LIU Y, LIU S, WANG Z. A general framework for image fusion based on multi-scale transform and sparse representation[J]., 2015, 24: 147-164.

[13] WANG Z, YANG F, PENG Z, et al. Multi-sensor image enhanced fusion algorithm based on NSST and top-hat transformation[J]., 2015, 126(23): 4184-4190.

[14] WANG Z, XU J, JIANG X, et al. Infrared and visible image fusion via hybrid decomposition of NSCT and morphological sequential toggle operator[J]., 2020, 201: 163497.

[15] 杨风暴. 红外偏振与光强图像的拟态融合原理和模型研究[J]. 中北大学学报: 自然科学版, 2017, 38(1): 1-7. YANG Fengbao.2017, 38(1): 1-7.

[16] LI H, WU X J. DenseFuse: A Fusion Approach to Infrared and Visible Images[J]., 2019, 28(5): 2614- 2623.

[17] MA J, YU W, LIANG P, et al. Fusion GAN: A generative adversarial network for infrared and visible image fusion[J]., 2019, 48: 11-26.

[18] 姜晓林, 王志社. 可见光与红外图像结构组双稀疏融合方法研究[J]. 红外技术, 2020, 42(3): 272-278. JIANG Xiaolin, WANG Zhishe. Visible and Infrared Image Fusion Based on Structured Group and Double Sparsity[J]., 2020, 42(3): 272-278.

[19] DONG W, LEI Z, SHI G. Nonlocally centralized sparse representation for image restoration[J]., 2012, 22(4): 1620-1630.

[20] ZHANG J, ZHAO D, GAO W. Group-based sparse representation for image restoration[J]., 2014, 23(8): 3336-3351.

[21] WANG Z, Bovik A, A universal image quality index[J].. 2002, 9(3): 81–84.

[22] Piella G, Heijmans H. A new quality metric for image fusion[C]//10th, 2003: 173-176.

[23] Xydeas C.S, Petrovic V, Objective image fusion performance measure[J]., 2000, 36(4): 308-309.

Visible and Infrared Image Fusion Based on Group K-SVD

WANG Zhishe，JIANG Xiaolin，WU Yuanyuan，WANG Junyao

(School of Applied Science, Taiyuan University of Science and Technology, Taiyuan 030024, China)

In the traditional image fusion method based on sparse representation, image blocks are used as units for dictionary training and sparse decomposition. The representation ability of dictionary atoms for image features is insufficient if the internal connection between the image blocks is not considered. Moreover, the sparse coefficients are inaccurate. Therefore, a fused image is not desirable. In view of the abovementioned problem, this paper proposes a fusion method based on the group K-means singular value decomposition (K-SVD) for visible and infrared images. Considering the image non-local similarity, this method constructs a structure group matrix using similar image blocks, and then, dictionary training and sparse decomposition are performed in the units of the structure group matrix by group K-SVD. Thus, this method can effectively improve the representation ability of dictionary atoms and the accuracy of the sparse coefficients.The experimental results show that this method is superior to the traditional sparse fusion method in terms of subjective and objective evaluation.

image fusion, non-local similarity, structure group matrix, group K-SVD

TP391.4

A

1001-8891(2021)05-0455-09

2020-08-20；

2020-10-24.

王志社（1982-）男，副教授，博士，研究方向为红外图像处理、机器学习和信息融合。E-mail：wangzs@tyust.edu.cn。

山西省面上自然基金项目（201901D111260）；信息探测与处理山西省重点实验室开放研究基金（ISTP2020-4）；山西省“1331”工程重点创新团队建设计划资助（2019 3-3）；太原科技大学博士启动基金（20162004）。