时标上时滞神经网络的牵制同步控制

蔡庆瑞，黄振坤,宾红华

(集美大学 理学院，福建 厦门 361021)

神经网络是模仿神经元信息传递过程所构建出的一种数学模型，近年来神经网络广泛应用于信息、图像等领域[1].早期的研究，大部分没有考虑信息传递具有一定的速度限制，因此没有考虑到信息传递过程中会产生时滞.事实上，在现实世界里可以找到很多受到节点时滞影响的动态网络系统，因此非常有必要将节点的时滞加以考虑[2].1989年，Macrus等首次建立了时滞神经网络模型，并研究了其平衡点的全局稳定性[3].文[4]在其基础上引入多时滞并研究了系统的全局指数稳定性，文[5]则在文[3]的基础上引入时变时滞且分析了系统的渐近稳定性.

同步是许多自然系统中的一种典型集群行为[6]，也是神经网络中研究的热点.但由于网络系统通常含有大量的节点，很难通过对每个节点添加控制器来控制一个具有大量节点的网络系统.为了降低控制器的数量，一种很自然的方法是通过控制一部分节点来控制整个网络达到同步.文[7]提出一种有效的牵制控制方法使动态网络达到平衡.文[8]通过讨论信号在网络中的传输，揭示牵制控制的机理.应用单一的控制器策略，文[9]讨论了一类具有非对称性和非线性的耦合复杂网络，给出了局部和全局耦合牵制同步的结果.

在实际问题中经常会遇到连续和离散交叉出现的情况，因而研究时标上的动态网络系统也具有重要的意义.Bohner等研究了时标上复值域神经网络的全局稳定性[10].文[11]证明了时标上多重时滞双向联想记忆神经网络周期解存在性和全局指数稳定性.时标统一并推广了连续情况下的微分方程和离散情况下的差分方程，在同时具有离散和连续的情况时，采用时标理论可省去大量的重复性工作，相关的理论和应用研究可参考文[12].本研究引入时标相关理论，分析复杂时域上具有时滞节点和线性反馈的动态网络牵制同步问题，利用不等式建立网络系统达到同步的充分条件，相关结果与文[13]的主要结论进行对比.

1 预备知识

时标T指的是实数集R的任意非空闭子集.当tt}；当t>infT时，后跳算子ρ:T→T定义为ρ(t)=sup{s∈T:st，则t是右扩散的；如果σ(t)=t，则t是右稠密的.函数μ:T→R+定义为μ(t)=σ(t)-t. 设函数f:T→R，若∀ε>0，∃δ>0，使得f在t的邻域上U(=(t-δ,t+δ)∩T)满足|[f(σ(t))-f(s)]-fΔ(t)[σ(t)-s]|≤ε|σ(t)-s|,∀s∈U则称f在t点是可导的，记fΔ(t)为f在t处的Δ-导数[14].定义[a,b]T=[a,b]∩T.

考虑一个包含N个线性耦合独立节点的复杂时滞动态网络，可用以下时标T上的动力系统描述：

(1)

其中：i=1,2,…,N,xi=(xi1,xi2，…,xin)T∈Rn为第i个节点的状态向量.f:Rn×Rn→Rn是连续可微函数.τ>0是常数时滞.A∈Rn×n是内耦合矩阵，C=(cij)N×N∈RN×N是网络的扩散耦合矩阵，cij=

在这个模型中，矩阵C不一定是对称的，元素cij可以不为0或1.而且内耦合矩阵A=(aij)n×n也不一定是对称的.

假设s(t)是下面孤立系统的唯一解：

sΔ=f(s(t),s(t-τ)).

初值为φ∈C，其中s(t)在相空间中可能为平衡点、周其轨道、非周期轨道和混沌轨道.

在开始主要结果之前，先提出一些必要的假设和引理以及条件.

条件(A1)[13]:对于向量函数f(x(t),x(t-τ))，满足标准Lipschitz 条件，即对于任意的x1(t)=(x11(t),x12(t),…,x1n(t))T和x2(t)=(x21(t),x22(t),…,x2n(t))T，存在常数L1L2>0使得

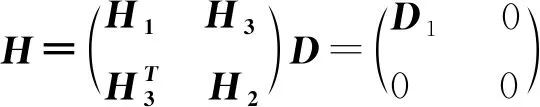
以上引理满足则要求控制增益di为无穷，但在实际系统中是不可能实现的，因此我们可以引入常数ε0解决这个问题.事实上，当λmax(H2)<0时，对于某些0<ε0<|λmax(H2)|，存在d>0，使得如果di>d，就有λmax(H-D)≤λmax(H2)+ε0<0.

定义1[6]对于任意的初始ψ∈C，若解xi(t)(i=1,2,…,N)满足

则称被控制的时滞动态网络(1)在时标意义上渐进同步.

定义误差向量：

ei(t)=xi(t;ψ)-s(t;φ)=0,i=1,2,…,N.

2 主要结果

假设选取l个节点i1,i2,…,il并用线性反馈控制器进行控制，可用如下方程描述

(2)

因此，被控制的网络(1)可以写成以下形式

(3)

不失一般性，可选前l个节点进行控制

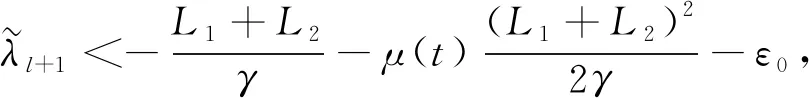
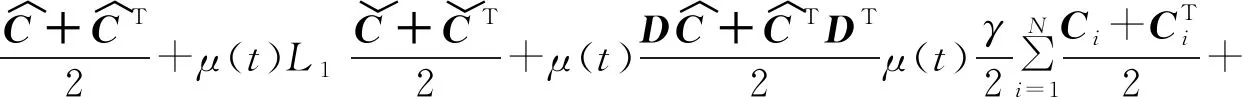
其中：当j=i或k=i且j≠i≠k时，上述矩阵对应位置的元素为-cijcik.

证明由于假设条件(A1)满足，建立Lyapunov函数：

(4)

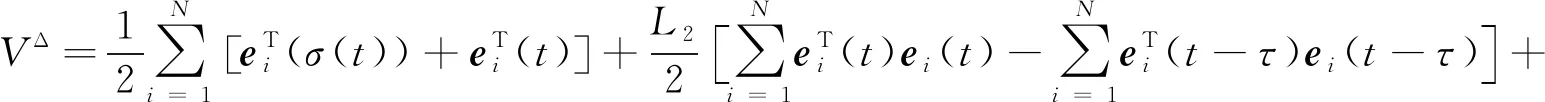
(5)

利用假设条件(A1)可得

(6)

(7)

其中,第一项：

(8)

第二项：

(9)

第三项：

(10)

第四项：

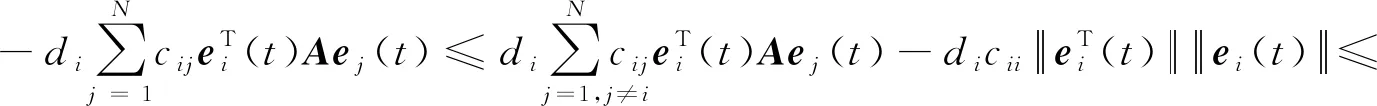
(11)

第五项：

(12)

最后一项：

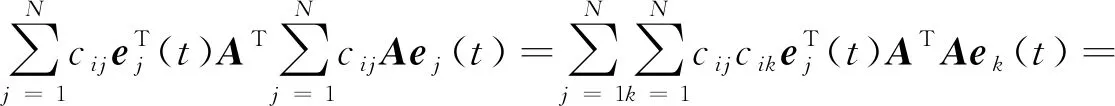
(13)

结合式(5)-(13)得，

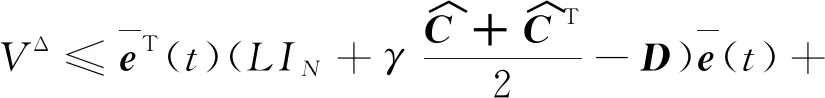
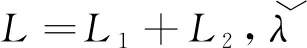
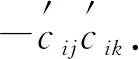
推论1取T=Z，τ∈Z，则根据时标理论可得系统(3)为

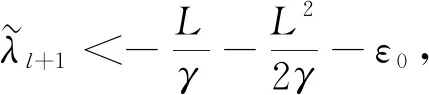
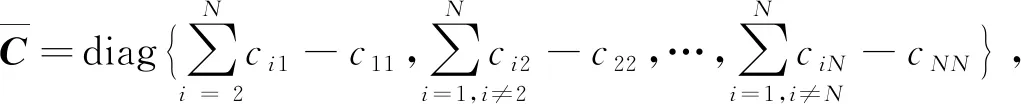
其中：当j=i或k=i且j≠i≠k时，上述矩阵对应位置的元素为-cijcik.

评论1根据定理1和推论1的结论，系统(3)不仅在连续和离散的情况下能达到时标意义上渐进同步，甚至在离散和连续交叉出现的复杂时域下也能达到时标意义上渐进同步，该结果将文献[13]的结论推广到了一般复杂时域上.

3 数值仿真

(14)

其中:f=(f1,f2)T,f1(xi(t),xi(t-τ))=-xi1+0.2tanh(xi1(t))+0.1tanh(xi2(t))-

0.1tanh(xi1(t-τ))+0.2tanh(xi2(t-τ)),f2(xi(t),xi(t-τ))=-xi2+0.1tanh(xi1(t))+

0.2tanh(xi2(t))+0.1tanh(xi1(t-τ))-0.5tanh(xi2(t-τ)).

图1 初值(2,1)的解(s1) 图2 初值(2,1)的解(s2)Fig.1 Solution of first component of condition (2,1) Fig.2 Solution of second component of condition (2,1)

根据定理1，系统(14)在线性反馈控制器(2)的控制下能达到时标意义上渐进同步，如图3和图4.

图3 系统误差(E1) 图4 系统误差(E2)Fig.3 System errors of first component Fig.4 System errors of second component

总之，本研究利用Lyapunov稳定性理论和时标理论，通过线性反馈牵制控制对具有时滞节点的动态复杂网络进行控制，得到了系统的同步准则.该准则不仅对连续的系统适用，对时间轴上同时具有离散和连续特点的系统也适用，是文[13]的改进，最后通过一个例子验证了所提出控制方法的有效性.