基于最大似然估计与卡尔曼滤波的室内目标跟踪*
(广州杰赛科技股份有限公司,广东 广州 510310)
0 引言
随着信息技术的快速发展,基于位置信息的服务(LBS,Location Based Services)已经成为信息化产业的重要基础,在移动互联网、物联网以及工业制造等领域发挥重要的作用。市场研究机构的分析数据[1]表明,室内定位市场规模的复合年增长率高达42%,在2020年将达到410亿美元。高精度的室内定位技术作为LBS的关键技术之一,近年来也得到了广泛的关注。
在室内定位场景中,基于Wi-Fi的定位技术是目前最为成熟的技术之一,在目前已经部署的室内定位系统中,约有一半采用了基于Wi-Fi的室内定位技术。典型的Wi-Fi定位技术主要包括基于传播模型测距的定位技术、基于信号到达时间测距的定位技术,以及基于信号指纹的定位技术等三类。基于传播模型测距的定位技术只适用于空旷的室内环境,如果室内环境复杂,间隔较多,会造成电波传播衰耗差异很大,从而带来较大的定位误差。基于往返时间测距的定位技术则需要在信号的帧结构中添加时间标签,需要基于特定的设备才能够实现。基于指纹匹配的定位技术具有对环境适应性强,不需要对现网设备进行改动的特点,是当前室内定位系统采用的主流技术[2-6]。
对于指纹定位技术来讲,主要面临两个方面的挑战。首先,信号指纹特征提取以及匹配算法对指纹定位的精度会有很大的影响。受到室内环境的影响,电波在室内传播时产生快衰落,造成接收信号在较短的时间范围内发生较大的波动,如何构建信号指纹数据库以及处理指纹匹配是现阶段面临的一个挑战[7]。另外,由于室内人员流动频繁,室内电波传播过程会受到室内人员的阻挡,引起测量误差,也会对定位的精度产生很大的影响。
针对当前室内定位技术存在的两个问题,本文的主要贡献是:提出一种基于最大似然估计与卡尔曼滤波的融合室内定位方法,首先采用最大似然估计进行定位,减小信号波动对定位结果的影响,然后再利用卡尔曼滤波算法对定位结果进行滤波处理,减小测量误差对定位结果的影响,最后通过仿真验证了所提算法的性能。
1 最大似然估计定位算法
定位算法可以分为两个阶段:离线阶段和在线阶段,如图1所示。在离线阶段,首先在需要提供定位服务的区域按照一定的间隔设置多个参考点(RP),然后在每个RP上收集接收信号的强度,建立指纹库。在在线阶段,移动终端将采集到的各个接入点(AP)的接收信号强度信息发送给服务器,服务器通过特定的匹配算法将终端所发送的指纹信息与指纹库中的数据进行匹配,从而完成对终端位置的估计。
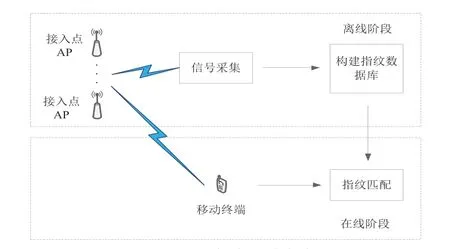
图1 指纹定位系统架构
1.1 构建指纹数据库
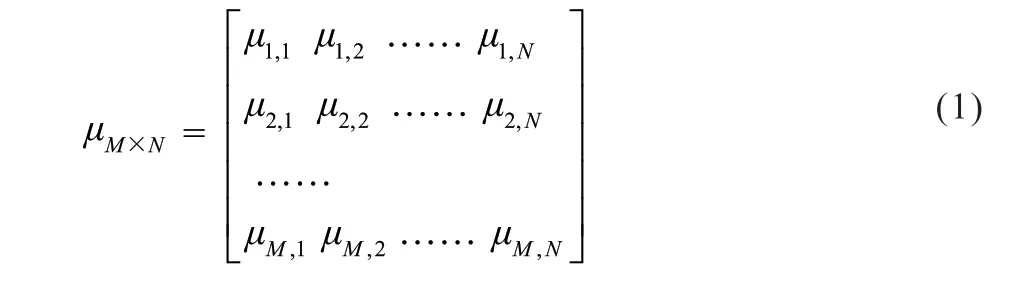
在离线阶段,在定位区域内共设置M个参考点{RPi,i=1,2…,M}上采集来自N个接入点{APi,i=1,2,…,N}的接收电平信息,构建指纹数据库,指纹数据库包含每个RP的接收信号均值与方差如式(1)、式(2)所示:
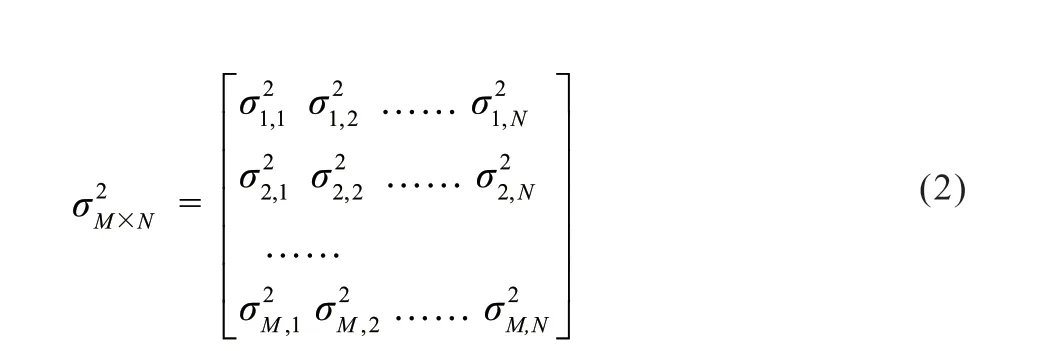
1.2 指纹匹配

则测量点与参考点RPi之间的似然函数可以表示为:
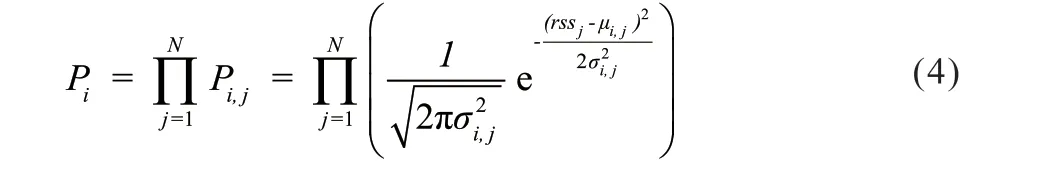
将RP按似然函数从大到小进行排序,取前K个RP的位置Lk进行加权作为测量点的定位结果。每个RP的权值ωk计算方法如下:

2 卡尔曼滤波
为减小测量误差对定位结果的影响,需要对定位结果进行滤波处理。参考文献[9-11]中采用了粒子滤波的算法,然而粒子滤波算法需要大量的粒子才能达到较高的精度,算法的计算复杂度高,不能满足实时定位需求。卡尔曼滤波[12]是一种最优的自回归数据处理算法,它可以利用上一时刻的估计值和当前时刻的测量值求出当前时刻的估计值,得到具有最小均方误差的估计结果[13]。相对于粒子滤波算法来讲,具有计算效率高的优点。
卡尔曼滤波主要包括状态预测与状态更新两个过程,如图2所示。在预测过程中系统根据终端内置传感器上报的运动状态信息对当前位置进行估计,得到当前位置的先验估计值以及方差;在更新过程中系统根据当前指纹定位的结果对先验估计值进行性更新,得到当前位置的后验估计值以及方差。
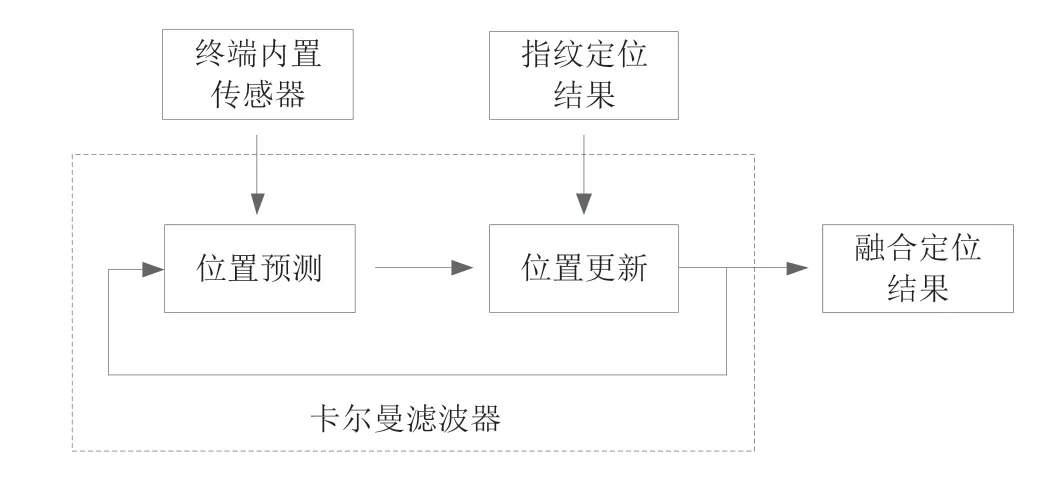
图2 卡尔曼滤波器系统架构
卡尔曼滤波器的预测方程为:


式(10)~(12)中,Fk为卡尔曼增益,H为观测矩阵,Zk为k时刻的位置测量值,R为测量噪声的协方差矩阵,即上一节中最大似然估计算法定位结果的方差。

x,y表示终端的坐标,vx,vy表示终端在两个坐标轴上的移动速度。
本文中将上一节基于最大似然估计算法得到的定位结果作为测量值Zk,则系统的测量矩阵可定义为:

3 性能仿真分析
3.1 仿真场景设定
某大厦二层的平面图如3所示,楼层的长度为32 m,宽度为23 m,在该区域内共部署了6个AP,如图3中的蓝色标记,每个参考点之间的间隔为0.8 m,如图3中的红色标记所示,并采用文献[8]中的射线跟踪模型生成参考点的指纹。图中的绿色标记表示终端的实际运动轨迹,分别采用最邻近算法、最大似然估计算法以及卡尔曼滤波算法对终端的运动轨迹进行跟踪。
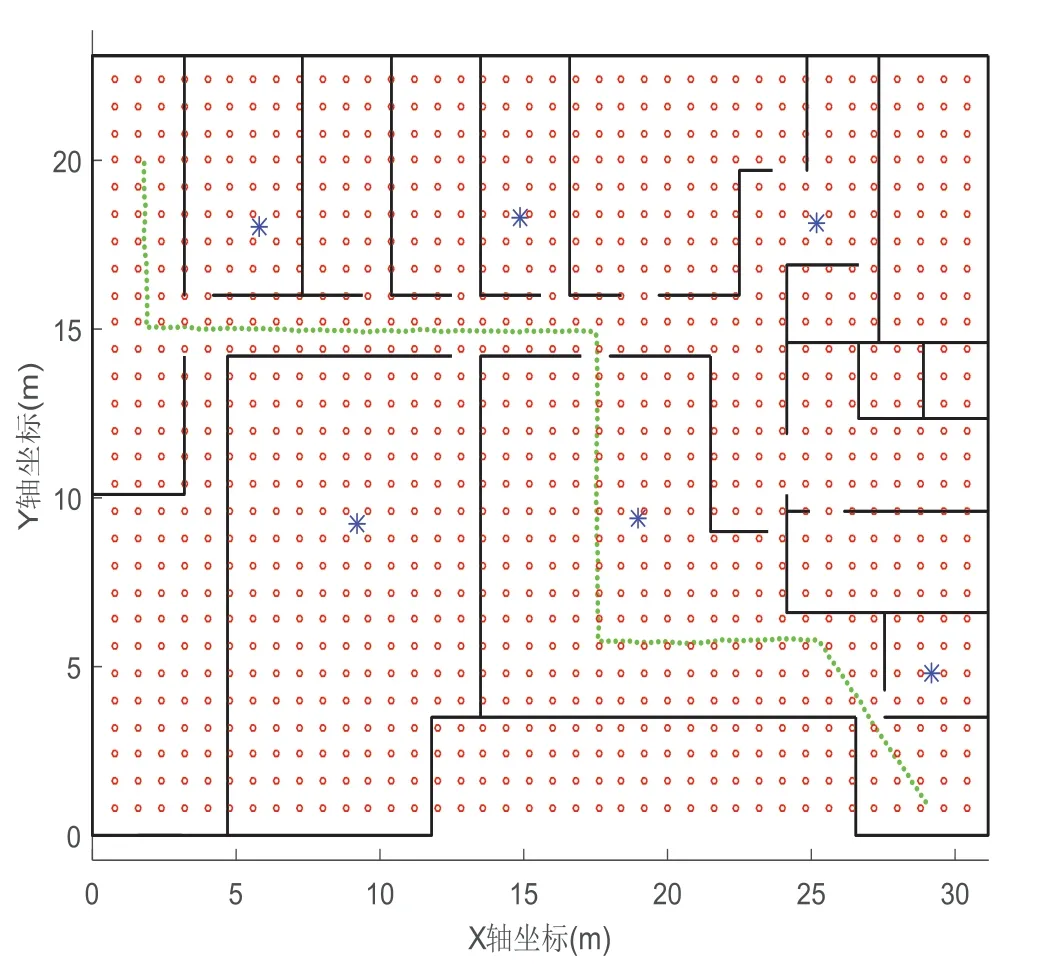
图3 仿真场景
3.2 仿真结果分析
图4为x坐标轴位置仿真结果,图5为y坐标位置的仿真结果。图中的绿色曲线表示目标移动的实际位置(Real),青色曲线表示最邻近算法的仿真结果(NN),蓝色曲线表示最大似然估计算法的仿真结果(ML),红色曲线表示经过卡尔曼滤波后的仿真结果(KF)。从图中可以看出,采用最邻近算法的所得到的轨迹的偏离度最大,最大似然估计算法采用指纹信号的统计特性作为判别准则,减小了指纹信号波动的影响,其定位结果要优于仅仅以指纹信号的欧式距离为判别准则的最邻近算法。并且在经过卡尔曼滤波后,有效消除了测量噪声的引起的抖动,使得定位的结果更加平滑,更加接近于实际的路径。
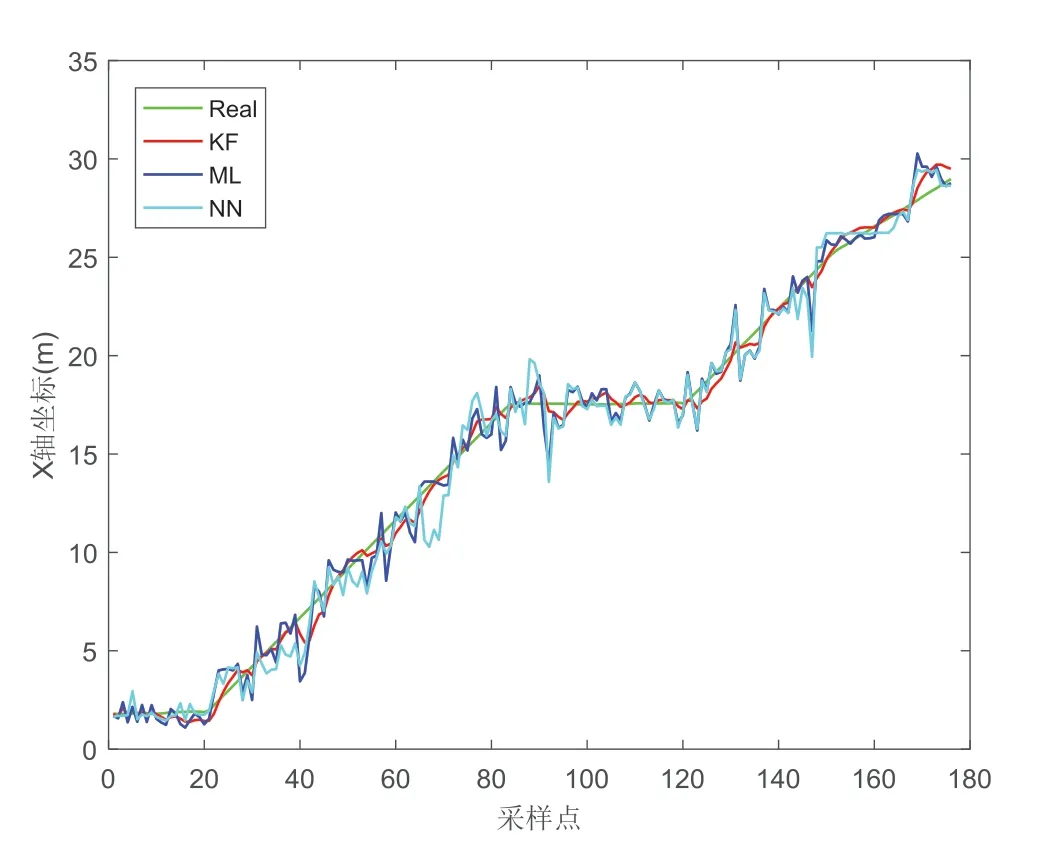
图4 跟踪算法轨迹对比(一)
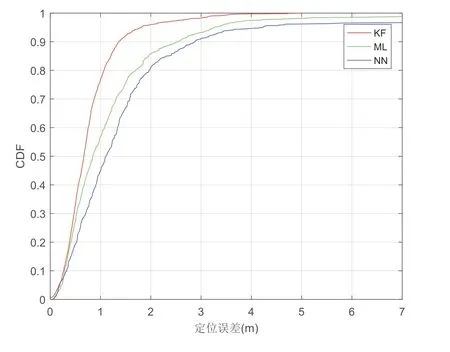
图5 跟踪算法轨迹对比(二)
三种算法的定位误差CDF曲线如图6所示。从图中可以看出,在测量误差为3 dB的情况下,最邻近算法的定位误差均值为1.19 m,最大似然估计算法的定位误差均值为0.85 m,比最邻近算法的性能提升了28.6%。而经过卡尔曼滤波的定位误差均值为0.65 m,比最邻近算法的性能提升了46.2%。
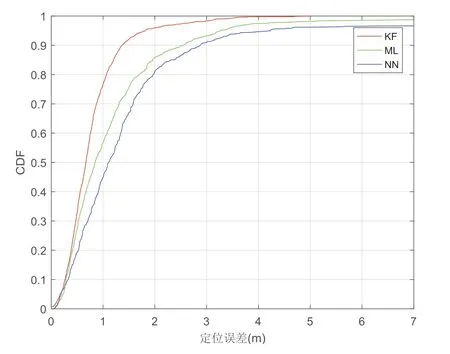
图6 定位误差CDF曲线
在室内环境下,人员流动是比较普遍的现象,人体阻挡、人流密度等因素都会对电波传播产生影响,导致终端对接收电平的测量误差,带来定位误差,因此有必要分析测量误差对定位性能的影响。本文假设测量误差在2~10 dB的情况下,对不同算法的定位误差进行了仿真分析,仿真结果如图7所示。从图中可以看出,随着测量误差的增加,最大似然算法的定位误差从0.77增加到1.48,卡尔曼滤波的定位误差均值从0.65 m增加到 1.15 m,相对于最邻近算法来讲,平均性能分别改善了16.7%以及48.0%。
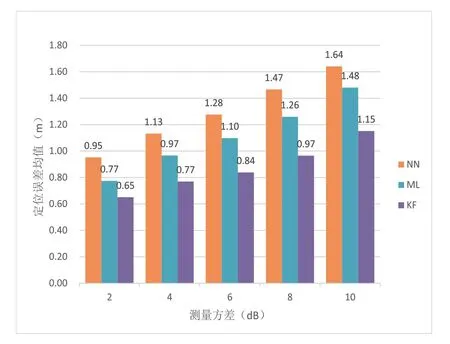
图7 定位误差仿真结果
4 结束语
本文提出了一种基于最大似然估计与卡尔曼滤波的室内目标跟踪算法。首先采用最大似然估计算法预测终端的运动轨迹,消除AP信号波动对定位结果的影响,然后再通过卡尔曼滤波对预测结果进行滤波处理,消除测量噪声对定位结果的影响,进一步提高定位的准确度。仿真结果表明,当测量误差为3 dB时,最大似然估计算法的定位误差均值为0.85 m,比最邻近算法的性能提升了28.6%;经过卡尔曼滤波后的定位误差均值为0.64 m,比最邻近算法的性能提升了46.2%。并且在不同的测量误差下对算法的定位误差进行了仿真分析,所提算法比最邻近算法性能提升了48.0%。
在采用最大似然估计进行指纹定位时,需要将测量到的信号与指纹库中的指纹逐一进行比对,算法的效率不高。在未来的工作中,可以考虑对指纹库的指纹进行聚类处理,按照相关度将指纹进行分类,以减少计算的复杂度,提高算法的效率。

