边坡软弱夹层宏-细观参数率定关系研究

阎 飞，梁 兵，孟轲荆

(北京京能地质工程公司，北京 102300)

0 引言

目前，人们对岩土介质的研究正处于由传统宏观尺度分别向细观尺度延伸的过渡时期，颗粒流方法(PFC2D/PFC3D)的兴起，为人们提供了一种宏细观研究的有效手段。PFC是基于Cundall[1]程序发展而来的颗粒流分析程序。Bock等[2]考虑土颗粒形态、结合水、自由水和固结后结构特征构建了新的模型。Utili、Nova[3]用PFC2D系统探讨了宏观强度参数与细观参数之间的关系。Park、Song[4]用PFC3D实现了节理直剪试验的三维模拟。张晓平等[5]用PFC2D分析了软弱夹层几何参数对试样力学行为的影响，认为当夹层厚度很小时，实质问题为岩土介质的接触问题，而夹层厚度较大时，实质问题为夹层的强度问题。周喻等[6]用PFC2D模拟了岩石节理直剪试验，从宏细观的角度探讨了节理的力学演化特征和破坏机制。颜敬等[7]运用正交设计和人工神经网络的方法，探索了宏细观参数之间的互演计算。丛宇等[8]分析了细观参数取值对弹性模量、泊松比、裂纹分布等宏观参数和形态的影响。徐金明等[9]结合花岗岩图像，建立了考虑细观组分实际分布的颗粒流模型，通过正交设计研究了宏细观力学性质关系和相应的调参方法。夏磊等[10]将层理面力学参数分为黏结强度、摩擦作用和咬合作用3个方面，研究了不同组合对层状岩体强度的影响。总结上述成果，可以发现通过PFC2D进行的宏细观参数研究主要集中在二维接触刚度模型、滑动模型、平行黏结模型和定义群组所涉及参数的标定上，虽然获得了一些定性的规律，但尚无法实现应用中的快速调参，针对颗粒间应力链和裂纹分布的演化研究明显滞后。

近几年来，国内的一些学者也从别的角度对细观尺度下的岩土介质开展了相关工 作。潘鹏志等[11]运用弹塑性理论、细胞自动机自组织演化理论、统计原理以及岩石力 学理论等，建立了模拟岩石三维破裂过程的张量型细胞自动机模型。罗荣等[12]基于岩石矿物种类及其含量提出了岩石矿物细胞元随机性参数赋值方法，探讨了岩石材料矿物细胞元弹性模量与宏观模量之间的函数关系。周翠英等[13]采用重整化群的方法概化出红层软岩的骨架构件和胶结物构件，推导计算了逾渗阈值。王益栋等[14]给出了颗粒破碎粒径的分布图，基于压缩破碎试验得到了分形维数。李学丰等[15]把组构张量和加载应力张量合成一个组合张量，定义了一个新的各向异性状态变量，并建立起各向异性破坏准则。这些成果丰富了人们的研究思路，一定程度上弥补了颗粒流方法的不足，具有很好的借鉴启示作用。但以DEM为核心，分析颗粒体系的细观结构及其运动规律，构建岩土介质宏细观参数关系依然是当前极富学术价值的基础研究课题，尚处于起步阶段。

本文利用颗粒流PFC软件和均匀设计的思想，通过平行黏结条件下的初步模拟、优化模拟，分自然休止角、无侧限抗压强度、直剪试验三种模式，对边坡软弱夹层的宏—细观参数率定关系进行了研究，并依据模拟中出现的演化现象，划分破坏模式，进而得到细观参数率定建议。

1 均匀设计原理

均匀设计是由方开泰和王元两位数学家于1978年创立的一种试验方法[16]，属于数论中的“伪蒙特卡罗方法”，其思想是要使试验点在维度空间中“均匀分散”，不同于正交设计的“整齐可比”，每个水平在试验中都出现且仅出现一次，试验次数大为减少，结果的处理多采用回归分析，范围由大至小，逐步对模型进行修正，提高精度。

1.1 均匀设计表

均匀设计表是试验设计的依据，具有三条特征：

1)各因素的水平试验次数仅为1次；

2)任意两因素的试验点在平面上，每行每列有且仅有1个；

3)任意两列之间的均匀性不一定相等，设计时应选择均匀性较好的列项。类似于正交设计表，每张均匀设计表都有一个代号Ua(bc)，其中U表示均匀设计，a为行数，表示试验总次数，b表示各因素的水平数，c为列数，代表最多能安排的因素数量。

1.2 均匀设计基本步骤

均匀设计的主要包括选评价指标、定影响因素、定试验水平、定设计表、回归分析、优化模型六步。具体在使用时可以采用多步线性回归分析实现。即先进行初步均匀设计分析，在初步分析的基础上做进一步的优化均匀设计分析。

由于均匀设计充分利用了试验点均匀分散的特性，可以大幅减少工作量，在确定自变量与因变量之间响应规律、筛选主控因素、参数率定等方面广泛适用。本文数值模拟所用到的软件PFC是利用宏观试验结果反演细观参数组(通常涉及5个参数以上的调参)，从而通过计算再现研究对象的力学响应过程，所以采用均匀设计手段对相关因素进行分析是必要而且合理的。

2 宏-细观参数演化关系

考虑到常规室内试验主要包括无侧限抗压和直剪试验，所以本文的宏细观参数研究以此两者为主，同时因为夹层体体现黏性土特性，将黏结模型统一选用为平行黏结，并增加仅存在摩擦参数fri作用时自然休止角试验的内容。

2.1 自然休止角模拟

对于自然休止角的模拟，采用散落模式，即在一定范围内随机生成颗粒，在其左侧与下方设定足够长墙体，施加重力自由下落，颗粒与下墙碰撞反弹后充分迭代平衡，最终形成斜坡角，此角度即为散落模式时的自然休止角，记为φ散，分初步模拟和优化模拟两步进行方案优化设计。

初步模拟。模型中设置set-disk-on，需要考虑的因素有总颗粒数N、颗粒密度ρ(因为有一定的弹性撞击)、墙体法向与切向刚度(Kwn、Kws)、颗粒法向与切向刚度(Kbn、Kbs)、摩擦系数fri共计7个。试验的次数取为因素数的4倍。选用表U28(288)进行各因素水平相等试验，第8个因素为评判指标φ散。为节省机时，模型中颗粒的粒径R处于单位cm级别，整个模型的范围取为长20 m，高12 m的矩形区域，粒子生成的横向区域为x向0～8 m，y向0.2～12 m，初始设定R为0.1 m，N为1000，颗粒粒径R随N的变化而调整，同时应满足墙体刚度大于颗粒刚度这一要求，故令N范围为1000～10000，ρ范围为1000～2700 kg/m3，Kbn与Kbs范围为107N/m～108N/m，Kwn与Kws范围为108N/m～109N/m，fri的范围为0.1～3.0。得出的散落模式(图1)。

以φ散为因变量，以N、ρ、Kbn、Kbs、Kwn、Kws、fri共计7个参数为自变量，对计算结果进行回归分析可以得到回归方程：

φ散=16+1.92e-3N-8.93e-3ρ+1.13Kbn+0.469Kbs+

433e-2Kwn+2.33e-2Kws+7.43fri

(1)

按照方开泰等人的计算方法[16]，各因素贡献率依次为24.8%、19.2%、8.55%、1.48%、1.27%、0.368%、38.7%。结果说明所试验的7个因素中，起主要因素的为摩擦参数fri、颗粒数N(粒径R)和密度ρ，颗粒体的法向刚度Kbn需要进一步分析，其余3个因素为非相关项。

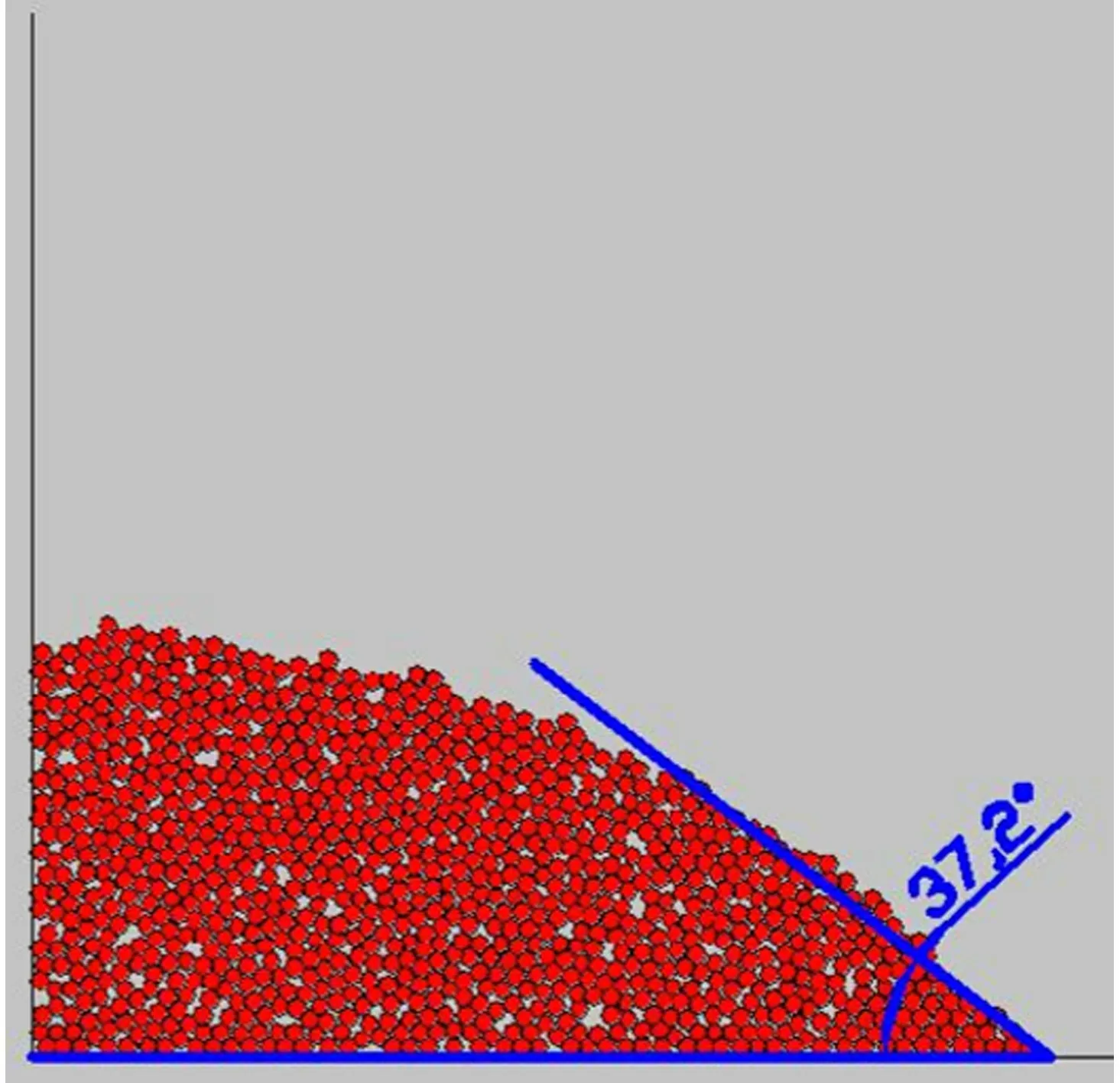
图1 散落模式示意图Fig.1 Schematic diagram of scattering mode

优化模拟。由初步的分析，进一步优化均匀设计方案，设置球的两向刚度相同，墙体刚度取为其10倍，以分析颗粒法向刚度Kbn对φ散的影响。试验次数取为因素数4的5倍即20水平，选用表U20(204)进行各因素水平相等均匀试验。粒子生成区间为x向0～8 m，y向0.3～15.3 m，下落距离统一为0.3 m，颗粒数N不再作为直接因素，而以粒径R代替，模拟粒组为粗砂0.5～2.0 mm，计算时为节约机时，统一将R扩大100倍，即为0.05～0.20 m，N由等面积换算得到(初始面积为0.1 m，N为1000时的面积)，ρ范围为1000～2700 kg/m3，Kbn范围为107N/m～108N/m，fri范围为0.1～1.5，评判指标取φ散。

以φ散为因变量，以R、ρ、Kbn、fri共计4个参数为自变量，对计算结果进行回归分析可以得到回归方程：

φ散=14.6-0.147R-8.16e-4ρ+3.36e-3Kbn+

16.4fri

(2)

各因素贡献率依次为0.707%、0.225%、0.0132%、61.8%，从中可以看出起主要因素的只有参数fri。

令生成区间为x向0～8 m，y向0.3 ～15.3 m，颗粒数N为1500，颗粒半径为0.1 m，球体两向刚度设置为106N/m，墙体两向刚度设置为107N/m，计算fri在0.1～1.5之间变化时，fri与自然休止角φ散的对应关系见表1。可以看到，φ当在0°～42°范围内时，φ与φ散只差Δφ基本处于12°之内，建议回归方程为

φ散=5.38+28.618fri

(3)

2.2 无侧限抗压试验模拟

对于无侧限抗压试验的模拟，参考丛宇等人的工作[8]，设定数值模型长100 mm，宽50 mm，初始颗粒半径最小为0.25 mm，最大为1.0 mm，采用半径扩大法生成指定孔隙率n的试样。试验前先利用四面墙体令颗粒充分平衡，再删去两侧约束，随后给上部墙体一个向下的速度进行加压，获得评判指标弹性模量E和极限抗压强度Rc。

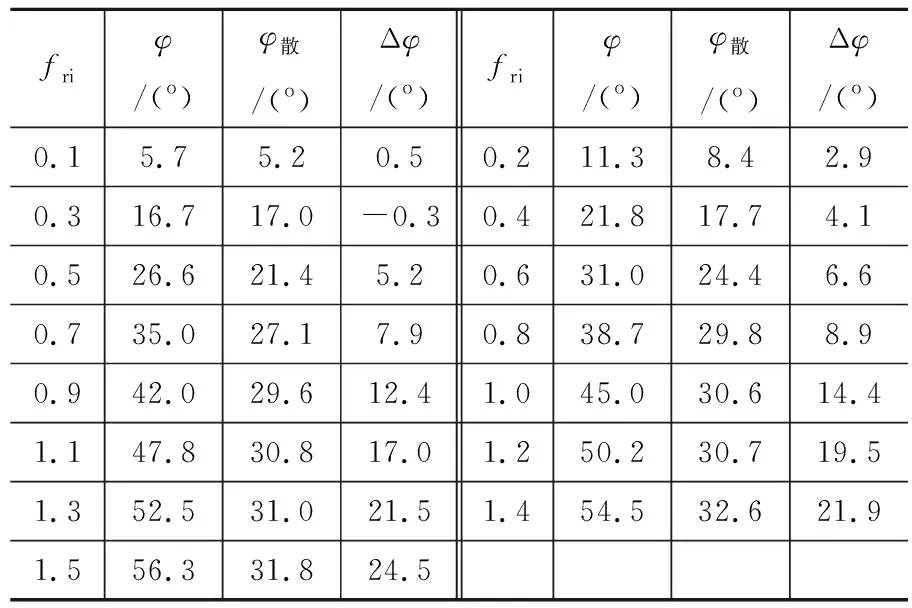
表1 自然休止角与fri关系Table 1 The relation between natural angle of repose and fri

初步模拟。由于黏结模型为平行黏结，故初步选定平行黏结切向刚度Kps、平行黏结刚度比Kpn/Kps、平行黏结法向强度Ppn、平行黏结切向强度Pps、平行半径乘子λ和参数fri六项为作用因素，研究平行黏结模型对E与Rc的影响。根据文献中正交试验所得结果，令试样n=0.20，颗粒法向刚度为23 GPa，切向刚度为8.8 GPa，密度ρ=2000 kg/m3，墙体两向刚度为200 GPa，同时Kps为10 GPa～40 GPa，Kpn/Kps值为0.2～5.0，Ppn为20 MPa～100 MPa，Pps为20 MPa～100 MPa，λ为0.1～1.0，fri为0.3～1.5。试验次数取为因素数6的4倍即24水平，选用表U24(246)进行各因素水平相等均匀试验。

模拟过程中，根据《土工试验方法标准》(GB/T 50123-2019)中相关条文，对有峰值试样取峰值点作为无侧限抗压强度Rc，而对无峰值试样取应变为0.15处的应力值作为Rc，弹性模量E通过近直线段的斜率计算得到。首先以E为评判指标进行回归分析，方程为

E=216+10.9Kps+61.1Kpn/Kps-2.83Ppn-

0.788Pps-56.6λ-77.5fri

(4)

各因素贡献率依次为23.3%、15.3%、11.2%、0.691%、0.452%、1.54%。结果表明，对于E而言Kps、Kpn/Kps值和Ppn显然为主控因素，其余三项居于从属地位，可不计。

然后以Rc为评判指标进行回归分析，可得线性方程如下：

Rc=-2.97+0.949Kps+2.31Kpn/Kps+0.126Ppn-

0.18Pps+19.5λ+3.05fri

(5)

各因素贡献率依次为16.6%、7.60%、7.69%、12.5%、18.7%、0.828%。由结果可知，对Rc而言，Kps、Pps、λ为主控因素，Kpn/Kps值、Ppn为次要因素，fri作用可忽略。

优化模拟。根据初步模拟的结果以及在自然休止角试验中获得的认识，分别以E和Rc为评判指标进行均匀设计方案优化。

指标E除平行黏结中的Kps、Kpn/Kps值、Ppn三个主控因素外，考虑颗粒及试样本身性质影响，将颗粒切向刚度Kbs、颗粒两向刚度比Kbn/Kbs和孔隙率n列为考察对象。墙体为体现加载板的刚性，依然取200 GPa，其余非分析项参数的取值分别为ρ=2000 kg/m3、Pps=80 MPa、λ=0.5、fri=0.8。而分析项参数Kbs范围为2 GPa～20 GPa、Kbn/Kbs值范围为0.2～5.0、n范围为0.05～0.50、Kps范围为2 GPa～20 GPa、Kpn/Kps值范围为0.2～5.0、Ppn范围为10 MPa～300 MPa，试验次数取为因素数6的4倍即24水平，选用表U24(246)进行各因素水平相等均匀试验。

对试验结果进行回归后可得

E=-339+0.366Kbs+2.49Kbn/Kbs+363n+

8.55Kps+8.55Kpn/Kps-0.0260Ppn

(6)

各因素贡献率依次为0.0953%、0.256%、58.6%、41.5%、6.69%、0.102%。上述结果说明，主控因素为试样孔隙率n和平行黏结切向刚度Kps，次要因素为Kpn/Kps值，剩余3项为可忽略项。

指标Rc类似处理，这里将平行黏结中的λ、Kps、Pps和试样颗粒的Kbs、Kbn/Kbs值、n共6项选为考察因素，取值如下：λ范围为0.1～1、Kps范围为2 GPa～20 GPa、Pps范围为10 MPa～300 MPa、Kbs范围为2 GPa～20 GPa、Kbn/Kbs值范围为0.2～5.0，n范围为0.05～0.50。其余非分析项参数取值依次为墙体两向刚度 200 GPa、ρ=2000 kg/m3、Ppn=80 GPa、Kpn/Kps=1.0、fri=0.8。试验次数取为因素数6的4倍即24水平，选用表U24(246)进行各因素水平相等均匀试验。回归可得

Rc=-32-0.00723Kbs+0.912Kbn/Kbs+36.8n+

11.6λ+0.372Kps+0.00952Pps

(7)

各因素贡献率依次为0.00419%、3.87%、67.9%、21.7%、8.87%、1.54%。结果表明，主控因素为试样孔隙率n和平行黏结半径乘子λ，次要因素为Kps、Kbn/Kbs值、Pps，Kbs为可忽略项。

在优化模拟过程中，试样的破坏形态和应力应变曲线见图2。

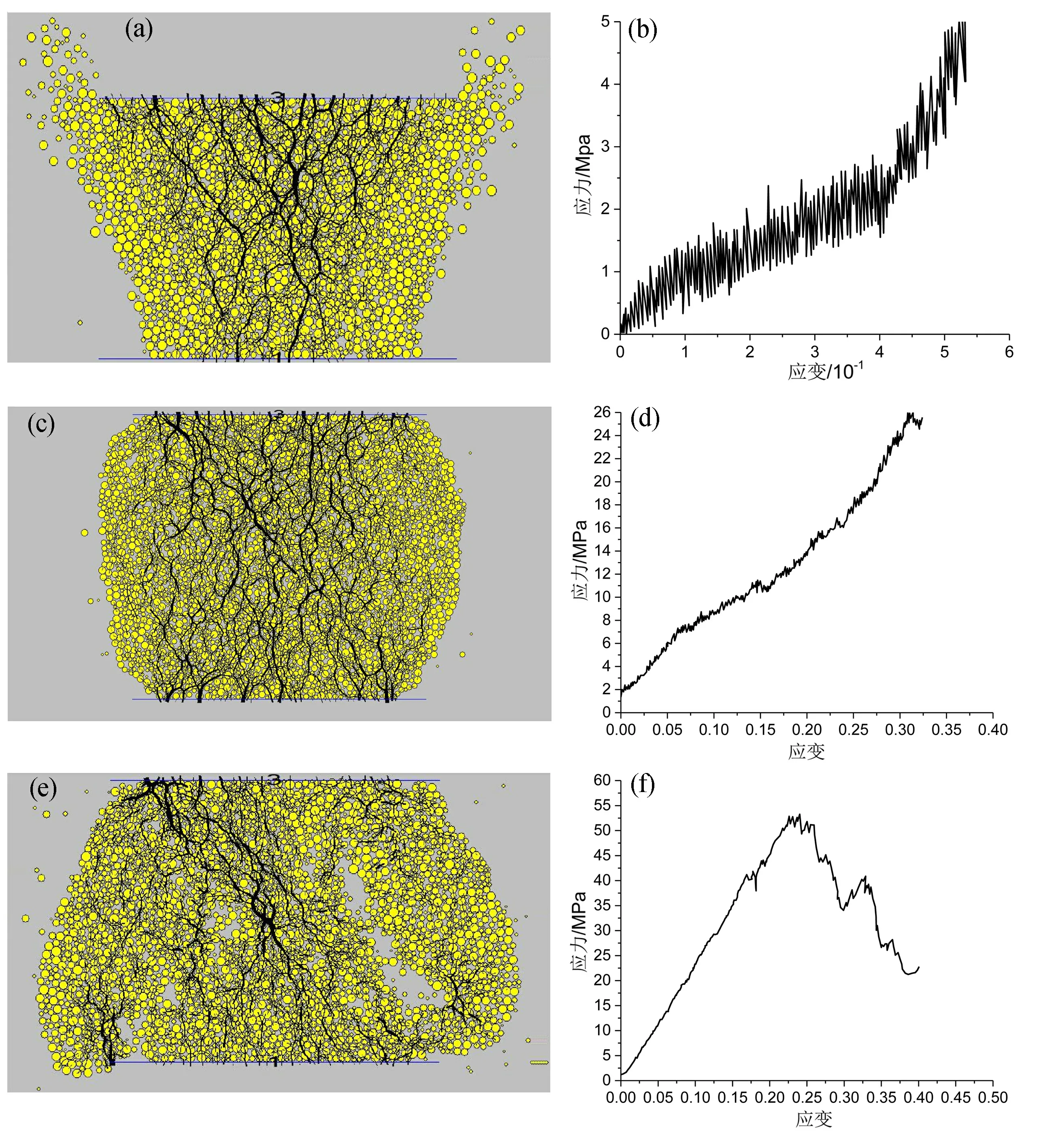
图2 试样破坏模式及其应力应变曲线Fig.2 Failure mode and stress-strain curve(a) 挤出式破坏 (b) 挤出应力应变 (c) 鼓胀式破坏 (d) 鼓胀应力应变 (e) 剪切式破坏 (f) 剪切应力应变

破坏形态分为三种，分别是挤出式、鼓胀式和剪切式，其中对于以E为指标的24个模拟试样，挤出式占37.5%(9个)，鼓胀式占58.3%(14个)，剪切式占4.2%(1个)，而对于以Rc为指标的24次试验，挤出式占33.3%(8个)，鼓胀式占66.7%(9个)，剪切式没有出现。结合均匀设计的结果，可以得到以下几点认识：① 试样的孔隙率n对无侧限抗压试验起重要作用，当n处于0.3～0.5之间时，试样破坏以挤出式为主。这是因为生成的颗粒之间空隙较大，自由生成时会出现部分颗粒脱空悬浮，从而使得试样整体性较差，当加载进行时，受压部分无法形成力链的有效传导，从而出现挤出效果，此时其应力应变曲线呈现宽幅稳定发展的态势，而当荷载作用范围传递至底层刚性板时，应力逐步产生集中，从而令曲线转而变陡。整体而言，挤出式破坏对于模拟高孔隙比软土试样较为合适。② 当n<0.3时，颗粒之间基本上都可以形成有效接触，平行黏结在荷载的作用下充分发挥作用，变形呈现出整体性，比较初步模拟和优化模拟结果可知，试样无侧限抗压强度试验的破坏模式主要为鼓胀式和剪切式两种，反映了中硬土、硬土和岩质试样的变形特征，且由其各自所占比例的变化推测，各参数之间存在某一界限式组合决定了试样的最终破坏形态。③ 观察图2e，试样的剪切破坏较为明显，残存体呈哑铃状，两端大中间窄，通过观察变形历史发现，试样起初为鼓胀式变形，到达一定程度之后，中心处颗粒突然张裂，随即形成一组近共轭的斜向裂隙，贯穿后试样逐步解体，并在一定程度上形成了新的应力传导途径进而再次发生剪切破坏，与其对应的是应力应变曲线上峰后发生的二次应力攀升。④ 初步模拟和优化模拟所筛选出主控因素的不同，部分源于破坏模式的差异，由于试验本身不存在拉力源，故其本质上均属于压剪，剪切面是否贯通直接影响了平行黏结切向参数的作用比例。

上述结果也进一步说明，利用颗粒流对岩土介质力学响应的试验模拟应首先明确其破坏模式，并以此为前提进行均匀方案设计和正交试验方案设计，从而做到有的放矢。

对所有模式而言，影响E的主控因素为孔隙率n和平行黏结Kps、Kbn/Kbs值，影响Rc的主控因素为孔隙率n和平行黏结半径乘子λ，其余参数项则需要结合破坏模式分析是否列入主控因素范畴。

2.3 直剪试验模拟

对于直剪试验的模拟，在周喻[6]等人工作的基础上进行，设定试样模型长100 mm，高40 mm，初始颗粒半径最小为0.3 mm，最大为0.525 mm，采用半径扩大法生成指定孔隙率n的试样。试验前先利用四面墙体令颗粒充分平衡，并编制伺服程序对试样上下墙体进行加压控制，保证压力达到模拟要求后，对试样进行横向剪切直至破坏，该过程可以获得典型的剪切曲线。重复该过程，即可得到不同压力下试样的破坏点，从而统计计算出试样的黏聚力c和内摩擦角φ。

初步模拟。由于黏结模型为平行黏结，故初步选定平行黏结切向刚度Kps、平行黏结刚度比Kpn/Kps、平行黏结法向强度Ppn，平行黏结切向强度Pps、平行半径乘子λ和参数fri六项为作用因素，分别模拟压力为0.25 MPa、0.50 MPa、0.75 MPa、1.00 MPa、1.25 MPa五种情况时试样的直剪试验，从而得到相应的c和φ值。

根据文献中提供的参数，令试样n=0.20，颗粒法向刚度15 GPa，切向刚度2.5 GPa，密度2750 kg/m3，墙体两向刚度为50 GPa，同时Kps为0.8～8.0 GPa，Kpn/Kps值为0.2～5.0，Ppn为1 MPa～40 MPa，Pps为1 MPa～40 MPa，λ为0.1～1.0，fri为0.3～1.5。试验次数取为因素数6的4倍即24水平，选用表U24(246)进行各因素水平相等均匀试验。

在24组试样模拟过程中，剪切曲线总体表现为直线型、硬化型和峰值型三类(图3)，其中硬化型又包含有硬化缓变型与硬化直线型两亚类。根据《土工试验方法标准》(GB/T 50123-2019)中相关条文，对峰值型取峰值剪应力作为抗剪强度，对其余试样取剪切位移4 mm所对应的剪应力作为抗剪强度，进而得到各组试样的c和φ值。

首先以c为评判指标进行回归，方程为

c=-411+59.3Kps+66.6Kpn/Kps-0.847Ppn+

0.471Pps+574λ-61.3fri

(8)

各因素贡献率依次为26.3%、12.1%、0.158%、0.039%、30.8%、0.638%。结果表明，对于c而言，λ、Kps、Kpn/Kps值是主控因素，其余三项居于从属地位，可忽略。

以φ为评判指标进行回归分析，可得线性回归方程：

φ=9.51+0.907Kps+0.308Kpn/Kps+0.0826Ppn+

0.0607Pps+9.87λ+2.87fri

(9)

各因素贡献率依次39.2%、1.65%、9.52%、4.12%、57.3%、8.91%。即对于φ而言，λ、Kps是主控因素，Ppn、fri是次要因素，而Pps、Kpn/Kps值作用可忽略。

24组试样中，上述四种类型所占比例分别为直线型∶硬化缓变型∶硬化直线型∶峰值型为9∶10∶2∶3，前两类占绝对多数。其中直线型主要表现为剪切时曲线宽幅振荡，低围压(0.25 MPa)条件下颗粒间力链发育不完全，而高围压下颗粒间联系则较好，同时伴随剪切的进程，试样有压密现象，曲线前部较陡后部呈一较缓直线形态。由动态过程记录可知，剪切的显著影响范围为2～3倍墙体长度，该现象普遍存在于所有模拟试样当中，剪切面及颗粒破坏形态由于细观参数的差异而不同，对于直线型表现为前部拖拽和后部下倾。硬化缓变型主要表现为，剪切曲线斜率逐渐变缓，振幅趋小，颗粒间力链发展较完全，剪切面也较为平顺。与之相比，硬化直线型由于颗粒间作用更强，剪切曲线振幅更小，趋于直线，力链发展更为完全，但剪切面不明显，前后部呈现出拖拽、翻转现象。峰值型的剪切曲线与岩土体的力学响应行为最为相似，表现为峰值后的软化现象，力链发展完全且剪切面较为平顺。

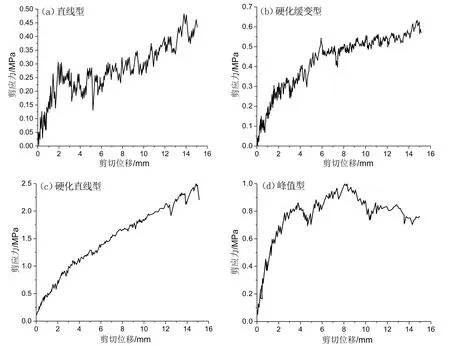
图3 试样剪切曲线类型

显然峰值型是下一步优化模拟的重点，故在选取λ和Kps为分析对象的基础上，加入球体细观参数的影响，分析其主控因素。同时根据已有试样的破坏形态，对模型进行缩减长度和增加墙体刚度的调整。

优化模拟。优化模拟中选定试样颗粒的Kbs、Kbn/Kbs值、n和平行黏结中的Kps、λ五项因素作为考察对象，分别模拟压力为0.25 MPa、0.50 MPa、0.75 MPa、1.00 MPa、1.25 MPa五种情况时试样的直剪试验，从而得到相应的c和φ值。根据初步模拟结果，令Kbs为2 GPa～20 GPa，Kbn/Kbs值为0.2～5.0，n为0.05～0.35，Kps为0.8 GPa～24 GPa，λ为0.1～1.0，同时Ppn为6.09 MPa，Pps为28.13 MPa，fri为1.187，Kpn/Kps值固定为1.0，密度ρ为2750 kg/m3，调整模型长度为75 mm，墙体刚度为200 GPa。试验次数取为因素数5的4倍即20水平，选用表U20(205)进行各因素水平相等均匀试验。

通过优化后20组试样的剪切计算，所得曲线总体隶属于峰值型和硬化缓变型两类，出现比例为10∶10，并且计算时步内均具有峰值或极大值，故取其对应点剪应力作为抗剪强度，进而由5个围压下的数据点，绘图得到各组试样的c和φ值。

对c进行回归方程为

c=-1060-16Kbs+114Kbn/Kbs+778n+

57.3Kps+1910λ

(10)

各因素贡献率依次为2.73%、9.80%、1.44%、46.5%、75.7%。结果表明，对于c而言，λ和Kps是主控因素，其余三项居于从属地位，可忽略。然后以φ为评判指标进行回归分析，方程

φ=31.8+0.273Kbs-2.87Kbn/Kbs+14n-

0.241Kps-4.99λ

(11)

各因素贡献率为9.71%、76.6%、5.68%、10%、6.35%，即对于φ而言，Kbn/Kbs值是主控因素，而Kbs、n、Kps和λ所占影响权重基本处于同一量级，起到局部调节作用。

模拟过程中出现了一些细观现象。首先是剪切破裂面的形态，如图4所示有三种情况。第一种为斜剪，存在于个别试样低围压0.25 MPa时，由于颗粒间随之挤压错动，当上表面集聚的应力明显大于初始应力时，试样局部发生抬动，剪切面随之向上发展，直至剪破试样，其应力位移曲线表现为近线性增大。第二种表现为中后部拱起，这种形态的形成主要是因为颗粒间本身的作用较强，而力链的传导效应有一定的过程和范围，中后部段颗粒体容易形成较难剪破的团粒，如同凸起一样阻碍了变形的发展，使得两侧无法很好协调，从而局部孔隙度增大，出现扩容，当剪切面爬升越过该部分后，试样完全破坏。这种现象在低围压向高围压转变的过程中较为常见，应力位移曲线表现为硬化缓变型。第三种形态，剪切面较为平顺，基本沿水平向发生破裂，图中由于上部颗粒的拖拽以及局部错动，形成较大的空隙，并且在模拟过程中，已破坏颗粒会随荷载板的运动重新发生黏合，力链再次形成发挥传导作用，也构成了部分的残余强度，试样的应力位移曲线是典型的峰值型。

其次是力链的发展演化，基本影响范围仍然是2～3倍墙体长度，发育密度低压力下稀疏，高压力下密集，试样随剪切的进行，左下角和右上角存在一定的应力遮蔽现象(图5)。此外，试样孔隙度的不同会对模拟所得强度的稳定性造成较大影响，在图6中列举了两种典型情况。其中密实型试样孔隙率低，由计算的20组结果统计，n<0.24，颗粒间相互接触较为容易，围压加载时细观结构相对保持稳定，库仑强度线符合线性规律。而松散型试样孔隙率较大，本次计算中主要是n处于0.24～0.35的剪切组，因为颗粒间联系并不充分，围压加载时试样便发生了一定的压密，从而改变了初始的细观结构，这就不难解释不同围压下抗剪强度点的离散特征，这样的情况有6组，但总体而言依然遵循压力越高，线性关系越显著的规律。上述现象也说明岩土体的结构性，包括宏观与细观两个方面，都会对最终的抗剪强度及其演化关系造成较大影响。

基于上述初步模拟和优化模拟的结果，可以得到直剪试验强度参数c和φ值与颗粒细观参数的基本关系如下：

1)对于黏聚力c而言，起主要作用的细观参数为平行半径乘子λ、平行黏结切向刚度Kps和平行黏结刚度比Kpn/Kps，影响权重为λ>Kps>Kpn/Kps，且均与c成正相关性，其他参数影响可以忽略不计。

2)对于摩擦角φ而言，颗粒本身的刚度比Kbn/Kbs

图4 剪切破坏面形态Fig.4 Shape of the shear failure surface(a)斜剪 (b) 中后部拱起 (c) 平顺

图5 剪应力遮蔽Fig.5 Shear stress shielding(a)初始段 (b) 剪切段 (c) 破坏段

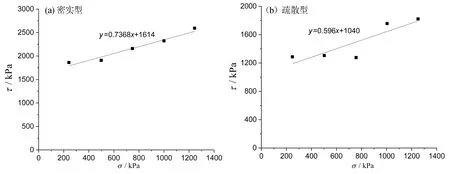
图6 孔隙率对结果影响

是主控因素，其与φ成负相关性，其他参数λ、Kps、Kbs、n属于次要因素，且各自影响权重相当。

3)孔隙率n的取值对于模拟过程中试样的力学响应行为影响较大，对于此次的模拟计算组，当n≤0.24时，颗粒间相互接触较为容易，围压加载时细观结构相对保持稳定，库仑强度线符合线性规律，而当n>0.24时，颗粒间联系并不充分，围压加载时试样便发生了一定的压密，从而改变了初始的细观结构，令抗剪强度统计点离散性增大。这一现象也从细观角度说明结构性是控制岩土体力学性能的重要因素。

4)细观参数平行黏结法向强度Ppn、平行黏结切向强度Pps和fri对于试样剪切行为的影响可以忽略，这三者都是决定颗粒与颗粒之间局部是否破坏和相互之间摩擦关系的，但对于宏观上力链的发展方向、发育程度以及试样的破坏模式等，并非主控因素。

5)24组试样的剪切结果表明，低围压向高围压转变的过程中，试样的破坏模式可能发生变化，具体表现斜剪、中后部拱起、平顺三种，并且高围压条件下更有助于提升数据点的稳定性，获得理想的剪切模拟效果。

6)由于剪切模拟过程中力链的动态演化范围有限，约为剪切板长度的2～3倍，故试样的长度不宜过长，留足剪切位移长度即可，否则可能会出现不合理的结果和现象，这也是尺寸效应的一种表现。

3 宏细观参数率定建议

通过对自然休止角、无侧限抗压强度和直剪试验的均匀设计，可以发现不同细观参数的组合对于模拟结果有着重要影响，主要体现在局部颗粒的响应行为、整体试样的破坏模式、强度参数的离散性等方面。结合已进行的工作和规律认识，对细观参数的率定进行讨论和建议。

1)fri反映的是颗粒之间的摩擦作用，但对于宏观上库仑定律中摩擦角的影响很小，可以忽略不计，该参数主要用于加速模型生成时不平衡力的迭代平衡以及调节颗粒细观上的响应行为。如对非黏性土体的模拟，当fri<0.1时，试样会出现局部挤出效应，这一特点可以用于模拟软弱夹层的挤出-滑移型破坏。

2)无侧限抗压强度试验模拟中，可以根据E和Rc的实测值对细观参数进行率定。对于E而言，主控因素为孔隙率n和平行黏结Kps，次要因素为Kpn/Kps值，三者均与E成正相关。对于无侧限抗压强度Rc而言，主控因素为孔隙率n和λ，次要因素为Kps、Kbn/Kbs值和Pps。

3)直剪试验模拟中，可以根据c和φ的实测值对细观参数进行率定。对于黏聚力c而言，平行半径乘子λ、平行黏结切向刚度Kps和平行黏结刚度比Kpn/Kps为主控因素，三者均与c成正相关。对于摩擦角φ而言，颗粒本身的Kbn/Kbs值为主控因素，与φ成负相关，其他参数λ、Kps、Kbs、n属于次要因素，且各自影响权重相当。

4)孔隙率n对于模拟结果的影响较大，主要是n的改变使得试样的细观结构发生了变化。体现在无侧限抗压强度试验模拟中，表现为当n处于0.3～0.5时，试样的破坏模式为挤出式，当n<0.3时，试样的破坏模式为鼓张式、剪切式；体现在直剪试验模拟中，表现为当n≤0.24时，颗粒间相互接触较为容易，围压加载时细观结构相对保持稳定，库仑强度线符合线性规律，当n>0.24时，颗粒间联系并不充分，围压加载时试样便发生了一定的压密，从而改变了初始的细观结构，令抗剪强度统计点离散性增大。上述两者均从细观角度说明结构性是控制岩土体力学性能的重要因素。

5)试样模型的构建中，纵向长度宜大于施压板长度的2～3倍，孔隙率n宜设置小一些，并且围压宜设置大一些，提升模拟结果的稳定性。

仔细分析上述几条建议，特别是细观参数与宏观参数之间的关系，不难发现他们具有很好的对应性。如c、Rc等强度参数的主控因素中，λ和n都起到了很大的作用，前者代表了颗粒间平行黏结的作用范围，而n则是通过细观结构影响破坏模式，最终改变试样的强度。同样在变形参数E的主控因素中，可以看到影响因素包括Kps和Kpn/Kps，其说明连接的侧向变形抵抗能力决定着试样纵向变形的响应情况。φ主要受到颗粒刚度比Kbn/Kbs的影响，fri作用可以忽略，其他因素对φ的影响权重基本处于同一量级。总结起来就是，n决定了初始试样的细观结构差异，λ决定了颗粒间黏结作用的范围，刚度和刚度比(包括球体和平行黏结)决定了力链的发育方向。

上述的建议和讨论可以为PFC的有效模拟与细观参数快速率定提供思路。即可以根据不同的试验项目，结合实测试验数据分别对主控细观参数进行分析，确定范围。例如直剪试验，可以先由φ获得Kbn/Kbs值的初步取值，再根据c确定λ、Kps和Kpn/Kps等参数也可以为无侧限抗压强度试验的细观参数确定提供借鉴；反之，对于同一种岩土体，无侧限抗压强度试验的参数组合也可以与直剪试验组对比校核。这样所得的细观参数会与宏观实际具有更好的一致性。在率定的过程中，应注意模型试样的长度设定，并且宜采用高围压条件，提升模拟结果的稳定性。

4 结论

利用颗粒流PFC软件和均匀设计的思想，通过平行黏结条件下的初步模拟、优化模拟，分自然休止角、无侧限抗压强度、直剪试验三种模式对岩土体的宏细观参数关系进行了研究，进而得到细观参数率定建议，所得主要结论如下：

1)对于非黏性颗粒，自然休止角与细观参数fri关系密切。

2)无侧限抗压强度模拟中，主要破坏呈现出挤出式、鼓胀式和剪切式三种类型。宏观参数弹性模量主要受控于孔隙率和平行黏结切向刚度。无侧限抗压强度主要受控于孔隙率和平行半径乘子。

3)直剪试验模拟中，破坏面有斜剪、中后部拱起和平顺三种典型形态。对于黏聚力而言，起主要作用的细观参数为平行半径乘子、平行黏结切向刚度和平行黏结刚度比。摩擦角主要受控于颗粒本身的刚度比。

4)孔隙率n对试样的力学响应有较大影响。试样模型的构建中，纵向长度宜大于施压板长度的2～3倍，孔隙率n宜设置小一些，并且围压宜设置大一些，提升模拟结果的稳定性。