乐坝火车站后山边坡降雨作用下渗流数值分析

李巧学，黄从俊，高 澍，方 甜，

(1.山东科技大学 地球科学与工程学院，山东 青岛 266590；2.中国地质调查局 成都地质调查中心，四川 成都 610081；3.四川省地质矿产勘查开发局403地质队，四川 峨眉 614200)

0 引言

在我国西南高山峡谷区，大量公路、铁路、居民区等都修建在高陡边坡中下部或坡脚平坦位置，尤其在多雨季节，极易发生边坡的破坏失稳，威胁生命财产安全。据统计，1980年以来，我国大陆所发生的大型灾害性滑坡约50%由强降雨直接触发，造成大量人员伤亡，经济损失巨大[1]，因此，许多学者在边坡稳定性做了大量相关研究工作，李修磊等[2]结合非饱和土强度理论，建立了边坡内单元土体达到临界破坏状态的判别方程，提出土质边坡浅层失稳由上缘张拉区、中间主滑动区和下缘挤压区组成；李梦姿等[3]基于Fredlund强度理论提出了允许土体破坏过程中产生剪切破碎的抗拉强度包线部分截断的非饱和土非线性强度准则；唐军峰等[4]结合现场详细工程地质勘察资料和监测资料，分析了堆积体边坡的结构特征和变形特征；刘顺青等[5]提出了可考虑不同块石含量、块石随机分布及基覆岩层倾角的边坡稳定性分析方法；田佳等[6]利用有限元程序研究了贺兰山青海云杉林边坡根土复合体对边坡稳定性的影响；苏永华等[7]改进了传统Green-Ampt入渗模型，并考虑干湿循环对土体强度的劣化作用，建立了间歇性强降雨下边坡稳定性表达式；李慧等[8]利用Abaqus有限元模拟软件分别模拟了轴平移技术实测的SWCC和应用修正计算方法修正的SWCC； 童志怡等[9]改进了传统条分法对边坡安全系数定义和使用的局限性，引入了条块稳定系数的概念；袁葳等[10]采用Karhunen-Loeve级数展开方法建立了土体抗剪强度参数的随机场模型，并在强度折减有限元法的基础上模拟了边坡失稳过程；石振明等[11]改进Green-Ampt入渗模型，提出适合多层非饱和土边坡降雨入渗的计算方法，将该方法应用于滑坡案例并进行稳定性评价分析；徐文杰等[12]运用数字图像处理技术，对西南地区某土石混合体边坡进行分析，建立其细观结构模型。目前，大多研究者都是建立理想模型并利用数学和力学理论结合数值计算程序来分析边坡渗流，或者结合实例边坡进行稳定性评价分析[13-14]，但是对考虑拉张裂缝同时强降雨条件下边坡稳定分析的成果较少。

基于此，本文以川藏铁路沿线乐坝火车站后山边坡为例，根据当地水文气象资料设计四种不同的降雨类型，利用Geostudio2012中seep/W模块，认为边坡后缘拉张裂缝已完全充水，对边坡瞬态和稳态渗流数值模拟分析，为以后研究不同降雨类型下边坡渗流更加深入研究提供借鉴和理论参考。

1 数值计算基础理论

在Geostudio2012渗流分析中，通常认为水在坡体土中流动服从达西定律，且服从饱和-非饱和渗流控制方程。

1.1 饱和-非饱和渗流控制方程

自然界中，持续性的强降雨促使边坡体内土由非饱和状态变为饱和状态，样的，在降雨间歇期，坡体内的降水随时间运移和蒸发，土介质又将处于非饱和状态。Richards以Darcy定律作为理论基础，提出了适合于饱和-非饱和土的渗流微分方程表达式[15]：

(1)

其中：H为总水头；kx为x方向渗透系数；ky为y方向渗透系数；Q为施加在边界的流量；mw为土水特征曲线(SWCC)的斜率；γw为水容重；t为时间。

为了将渗流控制微分方程应用到有限元程序数值计算分析中，应将渗流控制微分方程利用伽辽金加权余量法进行转化，转化后二维渗流有限元方程[16]为

(2)

(3)

其中：τ为单元厚度；[C]为单元渗透系数矩阵；[B]为梯度矩阵；{H}为节点水头向量；为插值函数向量；q为单元边界单位向量；t为时间；λ为瞬态渗流储水参数；A为单元面积；L为单元边界长度。

1.2 渗透系数特征曲线和土-水特征曲线

一般饱和土的渗透系数是一个恒定值，而非饱和土的渗透系数与体积含水率、残余含水率、饱和含水率等指标有关。根据对具有代表性边坡残坡积土样进行室内实验、现场试验及测试，绘制出坡体第四系松散残坡积土渗透系数特征曲线(图1a)和土水特征曲线(图1b)。

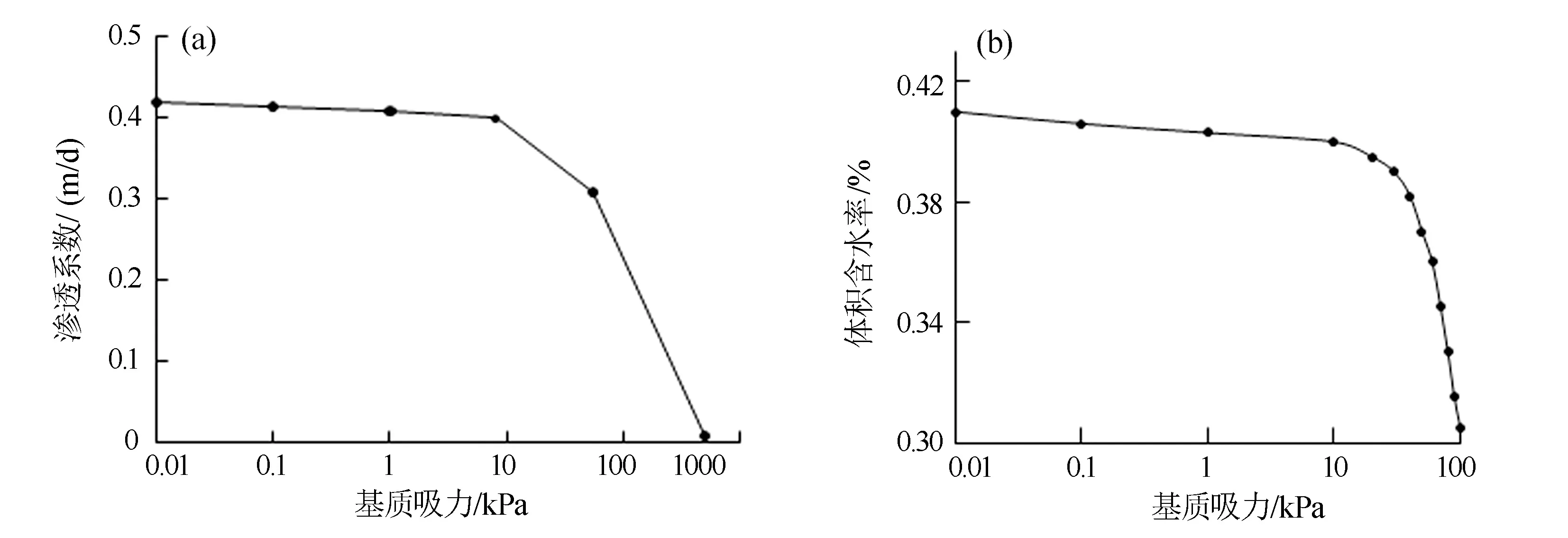
图1 渗透系数-基质吸力关系曲线(a)与体积含水率-基质吸力关系曲线(b)Fig.1 Permeability coefficient and matrix suction curve (a) and volumetric water content and matrix suction curve(b)

2 边坡基本概况

边坡区域常年雨季长达半年左右，秋季雨量最多，频率达73%，常年降雨量在1158～2163 mm之间，多年年平均降雨量达1663 mm，日最大降雨量达163 mm，时最大降雨量为75.1 mm，坡面发育大量季节性冲沟，大部分处于干涸状态，仅少部分处于富水状态，其流量一般为1 L/s～3 L/s，由于长期对边坡内入渗补给，使土体处于饱和状态，地下水主要为松散残坡积土孔隙水，受大气降水补给明显，水位和水量随季节变化较大，通常沿孔隙通道和基岩与土体接触面渗流，并排泄于前缘或两侧的冲沟，极少部分下渗补给基岩裂缝水，同时具有就近排泄的特点。

边坡基岩为古近系渐新统芦山组和古—始新统名山群组以及第四系，其中芦山组岩性以棕红色泥岩夹钙质粉砂岩为主，泥质结构，层状构造；名山群组岩性以暗棕红色泥岩夹杂色泥岩、钙质粉砂岩、灰色页岩为主，泥质结构，层状构造。第四系为残坡积松散堆积土，边坡纵向长约40 m，横向长约10 m，坡向61°，坡度约38°，两侧边界为陡缓交界处，前缘为冲沟；边坡体为第四系松散残坡积层含碎石粉质黏土，厚3～5 m，方量约1500 m3。由于持续强降雨边坡前缘失稳，淤积于沟道内，下部基岩为粉砂质泥岩，其产状为316°∠16°，属逆向坡(图2)。根据现场详细调查及访问附近村民，边坡上部存在拉张裂缝，并且中下部至下部每年均出现少量垮落现象。

3 数值计算模型及边界条件

边坡计算区域利用有限元程序自生网格，将网格划分为四边形单元和三角形单元，并就数值计算区域网格进行适当、加密，来保证数值计算分析的精度要求(图3)。设置节点数601个，单元数551个，坡面设置Ⅰ、Ⅱ、Ⅲ、Ⅳ 4种不同强降雨类型(图4)，设置坡面为降雨入渗边界，坡脚水位处及附近为渗出面边界，拉张裂缝位置为水头边界，持续时间设置为24 h，选取该地区最大时降雨量75.1 mm为4种降雨类型下降雨过程中最大参考值，饱和渗透系数(Ksat)为1.87 m/d，土体饱和重度(γsat)为19.8 kN/m3，有效内聚力(c')为11.6 kPa，有效内摩擦角(φ')为13.3°，吸力摩擦角(φb)为9°，在数值计算过程中建立上部监测点1#、中上部监测点2#、中下部监测点3#及下部监测点4#。

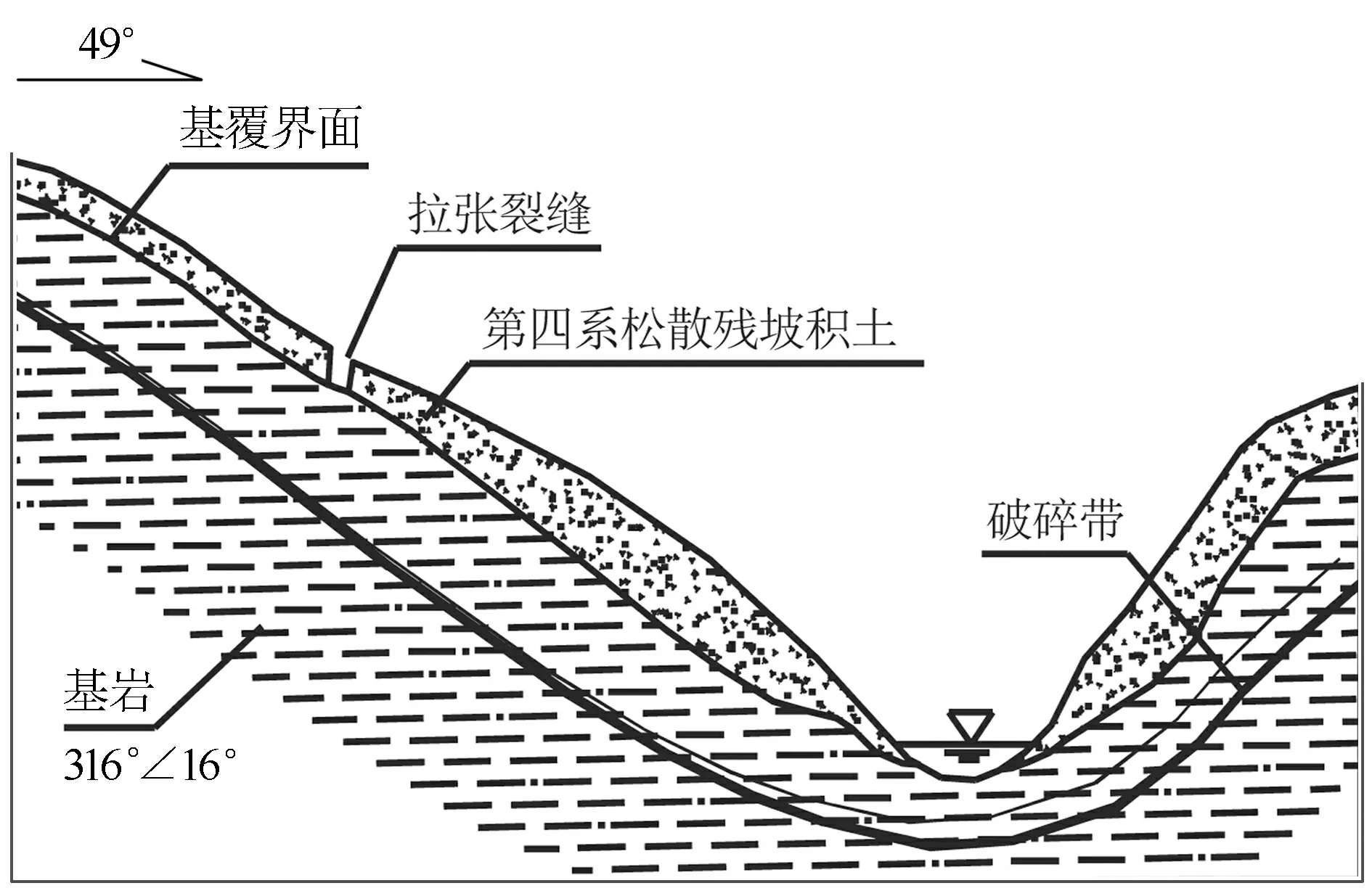
图2 边坡剖面示意图Fig.2 Schematic map of slope profile

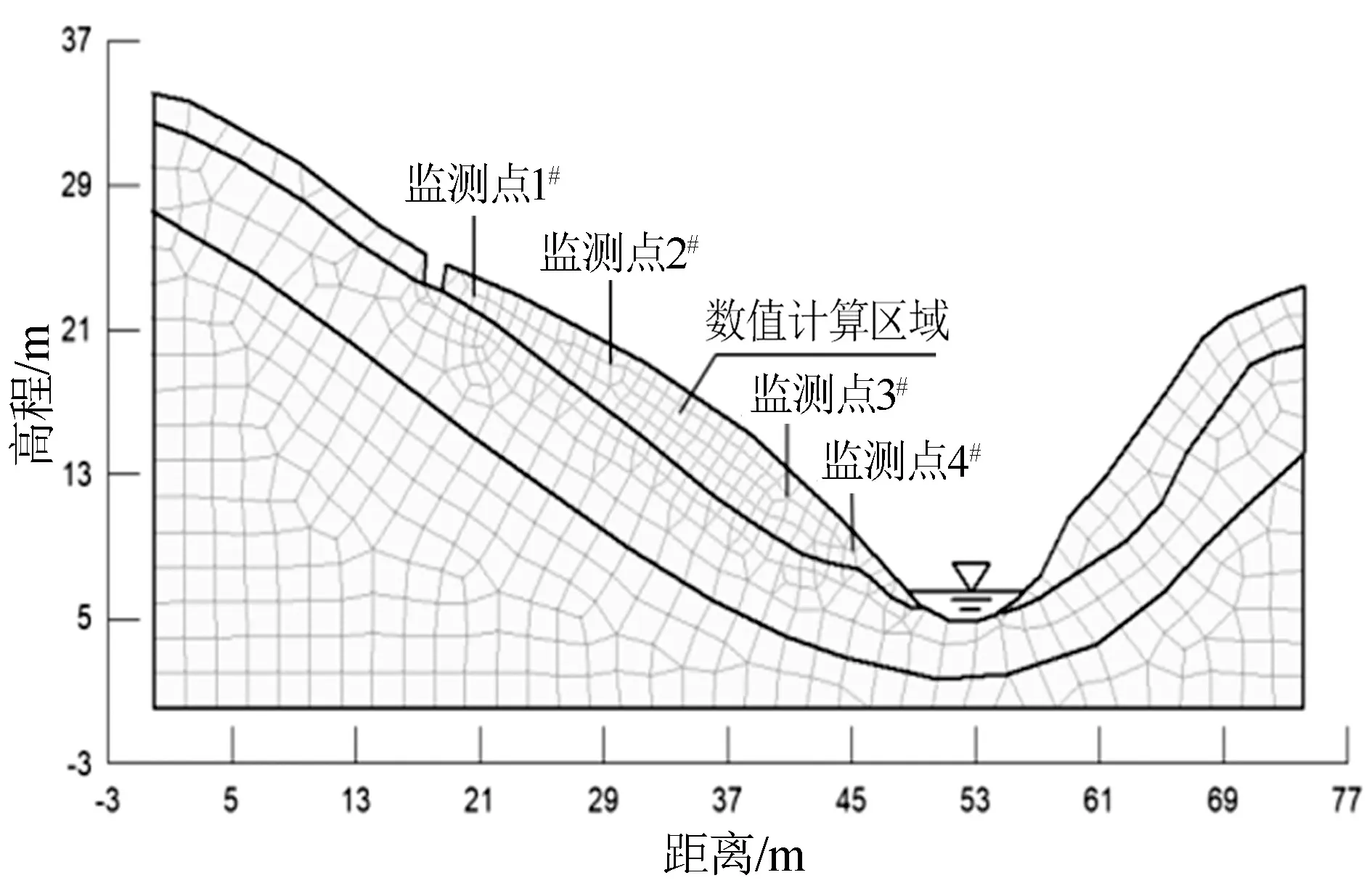
图3 边坡有限元计算模型Fig.3 Finite element calculation model of the slope

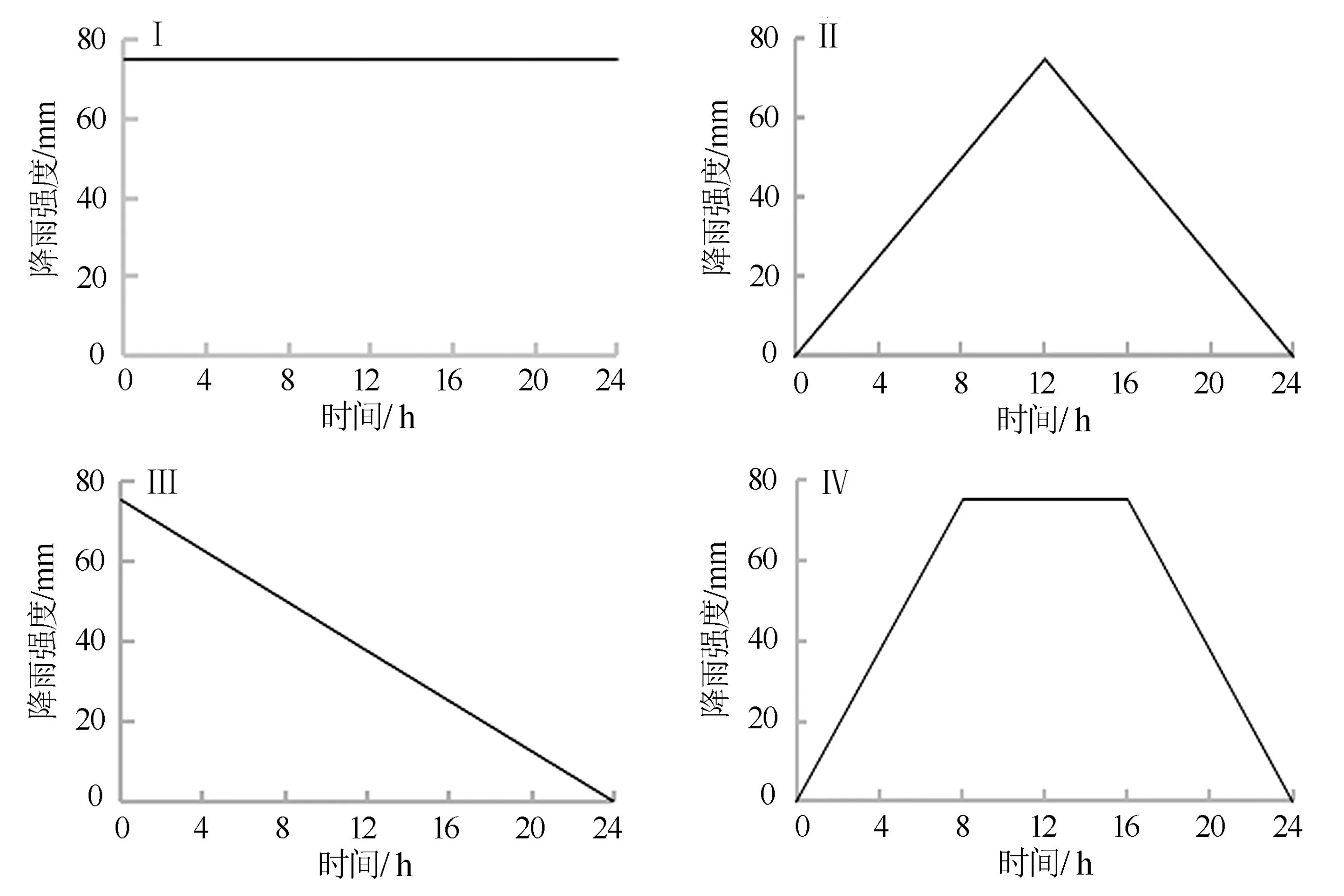
图4 四种降雨类型Fig.4 Four rainfall types

4 计算结果分析

4.1 稳态渗流分析

4.1.1 孔隙水压力随距离的变化规律

通过数值计算，由图5可知，坡体内不同位置孔隙水压力值不同，监测点1#、2#、3#、4#的孔隙水压力分别为-225 kPa、-185 kPa、-115 kPa、-84 kPa，随着距离的增大，负孔隙水压力随之减小，且孔隙水压力与距离基本呈直线关系，该关系可以用数学函数表达式y= 4.9399x-228.4 来拟合表示，从数学表达式可推求，距离越大，负孔隙水压力越小，这也充分说明越往坡顶位置，土体越处于不饱和状态，越往坡脚，土体越处于饱和状态，这与详细调查的坡脚位置更易发生失稳破坏相一致。

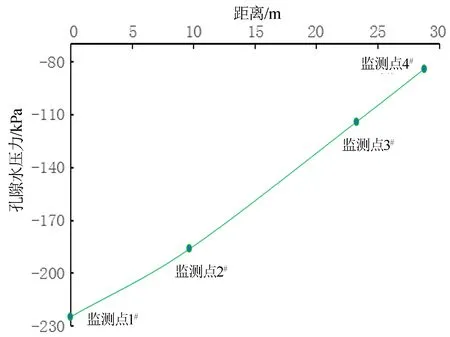
图5 孔隙水压力-距离曲线Fig.5 Pore water pressure-distance curve

4.1.2 渗流速度随距离的变化规律

根据稳态渗流数值计算，由图6可见，坡体不同部位渗流速度差异明显，在监测点1#X方向速度为4×10-5m/s，Y方向速度为3×10-5m/s；监测点2#X方向速度为6.8×10-5m/s，Y方向速度为5×10-5m/s；监测点3#X方向速度为1.2×10-4m/s，Y方向速度为1×10-4m/s；监测点4#X方向速度为3.4×10-4m/s，Y方向速度为2.35×10-4m/s。从监测点1#、2#、3#、4#的速度变化可以得出，速度均呈逐渐增加趋势，但是监测点1#、2#、3#的速度增加缓慢，并且总体呈直线增加，至监测点4#，速度增加迅速，同时，X方向速度大于Y方向速度，这说明在边坡渗流中，降雨入渗于坡体后X方向流速更快。

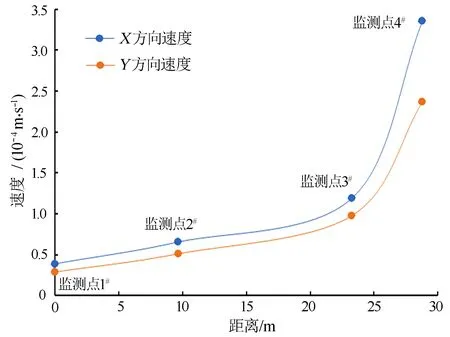
图6 渗流速度-距离曲线Fig.6 Seepage velocity-distance curve

4.2 瞬态渗流分析

4.2.1 孔隙水压力随时间的变化规律

由图7a可知，起始4个监测点1#、2#、3#、4#的孔隙水压力均为正值，它们分别为20 kPa、50 kPa、125 kPa、155 kPa，其中监测点4#孔隙水压力值最大，监测点1#孔隙水压力值最小，监测点2#、3#次之，这说明拉张裂缝充满水促使整个坡体内出现了正孔隙水压力；随着时间的延缓，监测点1#孔隙水压力先变为负值，随之依次是监测点2#、3#，最后监测点4#均成为负值；至大约36 min降雨作用后，4个监测点都完全成为负孔隙水压力，在36～78 min之间，负孔隙水压力继续增大，到78 min时达到最大，监测点1#、2#、3#、4#的孔隙水压力值分别为-240 kPa、-200 kPa、-125 kPa、-100 kPa；在78～20 min之间时，4个监测点的负孔隙水压力有所减少；至120 min时，监测点1#、2#、3#、4#的负孔隙水压力分别为-230 kPa，-190 kPa、-130 kPa、-75 kPa；在120 min之后，由图7可知，4个监测点位置孔隙水压力将不再发生变化，曲线将变为近水平直线，表明坡体中土非饱和—饱和程度达到了稳定状态。

4.2.2 渗流速度随时间的变化规律

在降雨类型Ⅰ作用下，由图8可知，在60 min之前，4个监测点位置X方向速度均呈不同程度的增加，监测点1#、2#、3#、4#的速度均由0分别增加到1×10-4m/s、3×10-4m/s、7×10-4m/s、1.6×10-3m/s，其中监测点1#速度增加最小，监测点4#速度增加最大；在60～144 min之间时，4个监测点速度出现急剧减少；至144 min时，监测点1#、2#、3#、4#的速度分别为1×10-5m/s、2.5×10-5m/s、8×10-5m/s、2.1×10-4m/s；在144～180 min之间时，4个监测点的速度将呈缓慢增加趋势，而监测点1#的增大趋势最不明显，监测点4#的增大趋势最明显，监测点2#、3#次之；至180 min时，监测点1#、2#、3#、4#的速度分别增加至2×10-5m/s、4×10-5m/s、1.2×10-4m/s、3×10-4m/s；至180 min以后，边坡体内速度基本保持不变。并且监测点1#在整个计算过程中速度最小，监测点4#在整个计算过程中速度最大，这说明在降雨过程中，坡体越接近坡顶渗流速度将越小，越接近坡脚渗流速度越大。

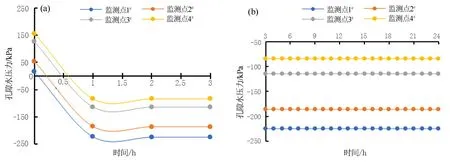
图7 孔隙水压力-时间变化曲线

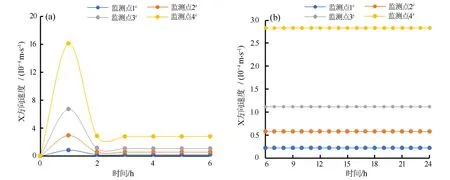
图8 降雨类型Ⅰ作用下X方向的流速随时间的变化规律Fig.8 Variation of velocity in X direction with time for rainfall type Ⅰ

在降雨类型Ⅱ作用下，边坡不同位置，速度将不同。由图9可知，在整个所设计降雨过程中，监测点1#速度最小，监测点4#速度最大，监测点2#、3#次之；在60 min之前，监测点1#、2#、3#、4#的速度均由0分别增加至8×10-5m/s、2.5×10-4m/s、5.5×10-4m/s、1.28×10-3m/s；至132 min时，4个监测点的速度重合，速度为-1.5×10-3m/s；在132～720 min之间时，监测点1#、2#、3#、4#的速度均由-1.5×10-3m/s分别增加到2.5×10-9m/s、6×10-5m/s、1×10-4m/s、2.65×10-4m/s，在720 min之后，4个监测点的速度呈直线型减小，最后速度都成为0。

由图10可知，在降雨类型Ⅲ作用下，监测点1#的速度最小，监测点4#的速度最大，监测点2#、3#次之；在60 min时，监测点1#、2#、3#、4#的速度均由0分别增加至8×10-5m/s、3×10-4m/s、6.8×10-4m/s、1.58×10-3m/s；在60～132 min之间时，监测点1#、2#、3#、4#的速度分别减至2×10-5m/s、4×10-5m/s、7×10-5m/s、2.1×10-4m/s；在132～180 min之间时，监测点1#的速度基本保持不变，监测点2#的速度增加至5×10-5m/s，监测点3#的速度增加至1×10-4m/s，监测点4#的速度增加至2.7×10-4m/s；在180 min之后，4个监测点的速度基本呈直线减小，到最后速度减为0。

由图11可知，在60 min时，监测点1#、2#、3#、4#的速度分别为7×10-5m/s、2.4×10-4m/s、5.7×10-4m/s、1.47×10-3m/s；在60～132 min之间时，监测点1#、2#、3#的速度均减至0，监测点4#的速度减至4.5×10-5m/s；在132～480 min之间时，监测点1#、2#、3#、4#的速度分别增加至2×10-5m/s、5.7×10-5m/s、1.12×10-4m/s、3.2×10-4m/s；在480～720 min之间时，4个监测点的速度基本保持不变；而到720 min之后，4个监测点的速度出现持续性减少，直到最后速度减为0。

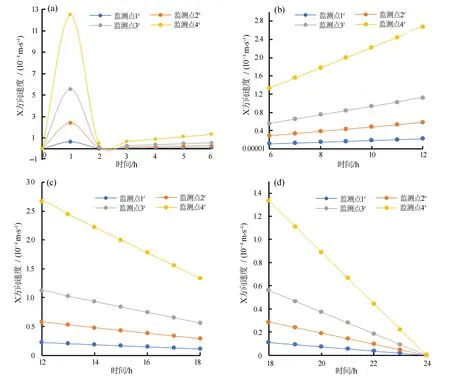
图9 降雨类型Ⅱ作用下X方向的流速随时间的变化规律Fig.9 Variation of the velocity in X direction with time for rainfall type Ⅱ

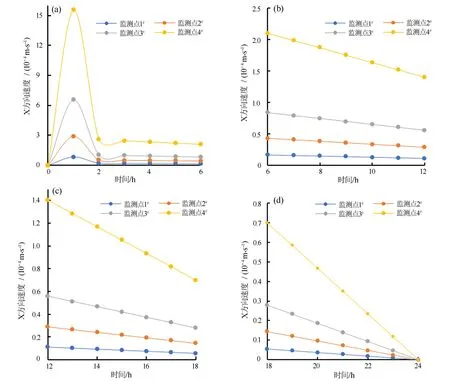
图10 降雨类型Ⅲ作用下X方向的流速随时间的变化规律Fig.10 Variation of the velocity in X direction with time for rainfall type Ⅲ

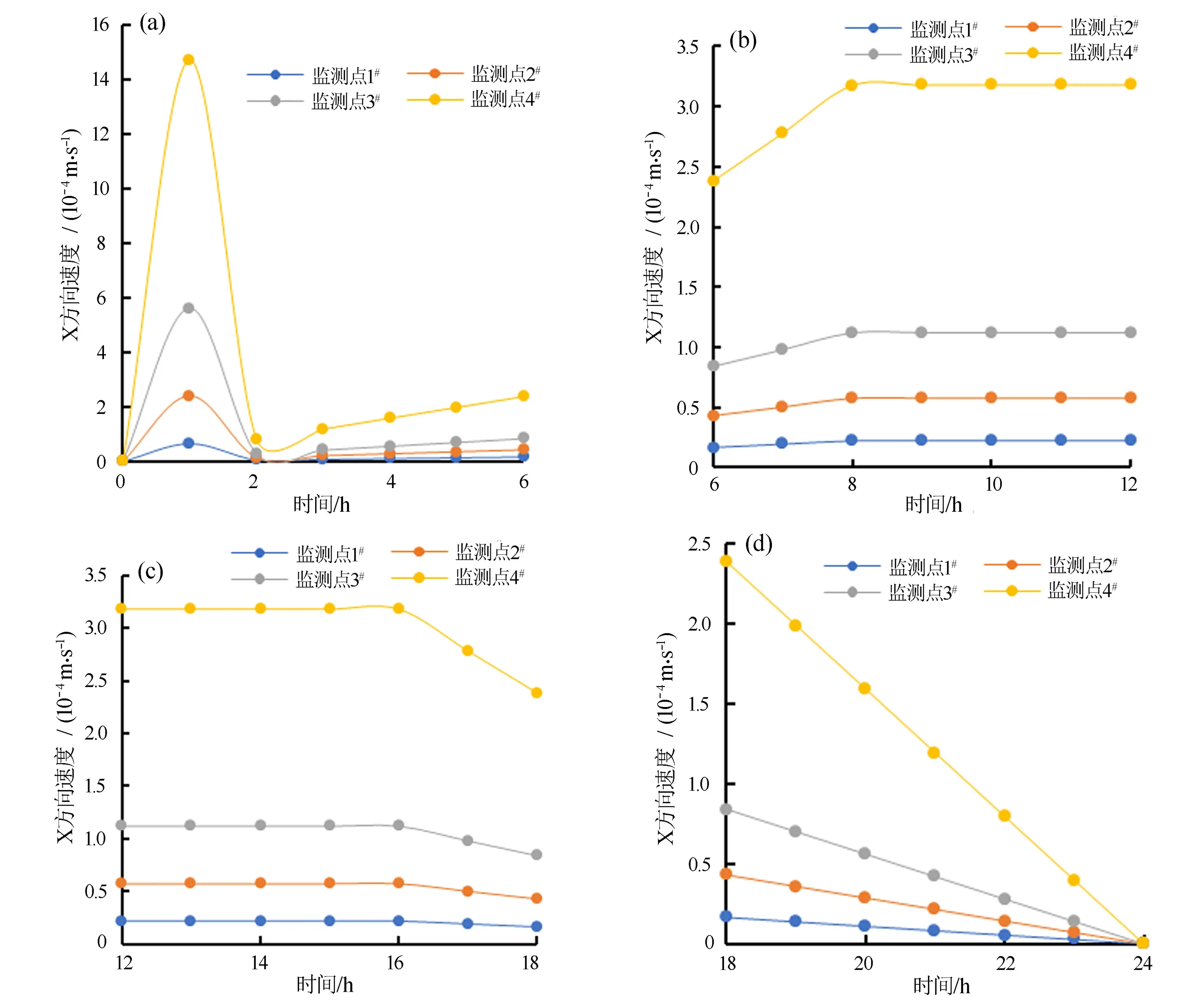
图11 降雨类型Ⅳ作用下X方向的流速随时间的变化规律Fig.11 Variation of the velocity in X direction with time for rainfall type Ⅳ

5 结论

1)通过稳态渗流分析，拉张裂缝壁面将为渗流边界，由于降雨受势能的影响，在边坡上部，负孔隙水压力值最大，在边坡下部，负孔隙水压力值最小，即坡体土从边坡上部不饱和到边坡下部趋近饱和；同样，边坡不同位置渗流速度也存在差异，边坡上部速度最小，边坡下部速度最大，且X方向速度大于Y方向速率。

2)通过瞬态渗流分析，在考虑拉张裂缝注满水情况下，整个坡体出现正孔隙水压力，最初边坡上部正孔隙水压力值最小，边坡下部正孔隙水压力最大，随着时间延续，整个坡体中孔隙水压力由正值变为负值，最后，坡体中负孔隙水压力值将不随时间发生变化。

3)在瞬态渗流中，边坡渗流速度受拉张裂缝充水条件和降雨类型影响较大，约1 h，4种降雨类型下坡体中速度出现了峰值，随后又急剧减小，减小到一定程度后速度的变化出现了和降雨类型一致的情况。随降雨类型不同，则渗流速度峰值将呈现差异。根据数值计算结果显示，降雨类型Ⅰ作用下计算峰值最大，降雨类型Ⅱ作用下计算峰值最小。

4)对比4种降雨类型中4个监测点渗流速度值的变化后可以看出，4种降雨类型中监测点1#的渗流速度最小，监测点2#、3#次之，监测点4#渗流速度最大。因此渗透力将越大，这充分说明降雨型失稳边坡出现在边坡中下部至下部的一个重要原因。

5)无论是稳态渗流数值计算还是瞬态渗流数值计算，其计算结果表明，越往边坡上部，正孔隙水压力越小，负孔隙水压力越大；越往边坡下部，正孔隙水压力越大，负孔隙水压力越小；越往边坡上部，渗流速度越小；越往边坡下部，渗流速度越大。