斜波压缩下HMX 晶体的弹塑性行为*

种 涛，莫建军，郑贤旭，傅 华，蔡进涛

（中国工程物理研究院流体物理研究所，四川 绵阳 621999）

炸药的力学性能参数与其反应机理和化爆安全性紧密相关[1-4]。单质高能炸药由于受到炸药大单晶生长困难的影响，不能直接加工成药柱等构件。目前，炸药力学性能均基于非均质炸药(PBX)为研究对象。研究表明，单质炸药的晶体特性对PBX 的性能如感度、安定性、机械强度等有重要影响[5-12]。

HMX 是目前综合性能最好的高能炸药，在武器中应用广泛。HMX 晶体因具有较多晶型以及复杂的相变问题而受到广泛的关注，它具有β、δ、α 和γ 等4 种晶型, 其中β-HMX、δ-HMX 和α-HMX 是固体，γ-HMX 是液体[13-15]。 这几种晶型具有不同的稳定性和对外界刺激的敏感程度, 不同相之间可以发生相互转变。在常温常压下, 4 种晶型的稳定性由强到弱依次为为β、γ、α、δ[14]。 β-HMX 是在室温下最稳定的晶型[15]。人们已开始研究HMX 在动态加载条件下的非弹性行为[16]。 Menikoff 等[17]和 Dick 等[18]的实验研究结果表明，β-HMX 单晶受平面冲击加载后呈现各向异性的弹塑性波结构。 Dick 等[18]的认为对于这种脆性的分子晶体，其主要作用机制是塑性机制。Jaramillo 等[19]通过分子动力学计算发现，β-HMX 的弹塑性转变机制是位错滑移运动。Sewell 等[20]和Zaug 等[21]也对β-HMX 单晶的弹塑性行为开展了冲击加载实验研究。

冲击加载下炸药单晶温升剧烈，由于其动力学响应特性的高感度，很难获得较高压力下的实验结果。利用斜波加载实验技术[22]，样品压缩过程中获得高压状态的同时依然可以保持样品材料中较低的温升，炸药不易发生化学反应。本研究利用磁驱动加载实验技术，开展了斜波加载下β-HMX 两个晶向在15 GPa 内的动力学响应研究，目的在于通过双光源外差测速技术（dual laser heterodyne velocimetry,DLHV）测量单晶的速度响应曲线，获得β-HMX 单晶不同晶向弹塑性转变信息的同时获得炸药的压力-相对比容关系。

图 1 HMX 晶体Fig. 1 An HMX crystal

1 HMX 单晶炸药的斜波压缩实验

HMX 是一种具有各向异性力学性能的单斜晶体，本文中采用的厘米量级大块体样品由中北大学制备，样品如图1 所示。

HMX 晶体斜波压缩实验条件见表1，HMX单晶样品有（011）、（010）两个晶向，实验窗口为LiF 单晶，加载电极为高导纯铝材料。单发实验对不同厚度样品进行斜波压缩，利用DLHV 测试HMX 样品/LiF 窗口的界面速度。

本文进行了2 轮实验：第1 轮实验完成了1 发HMX（011）晶向实验和3 发HMX（010）晶向实验；第2 轮实验降低了加载压力，2 种晶向各完成了1 发实验。第1 轮实验获得的速度历史曲线见图2～5，4 发实验都是两组不同厚度的HMX 晶体上下对称布局。第2 轮实验获得的速度历史曲线见图6～7。由实验结果得，速度波剖面都是弹塑性双波结构，且在弹塑性转变区出现了明显的速度松弛现象，有十几米每秒的速度降低。实验2 和实验3 实验结果显示，在厚样品的塑性后形成了冲击波。实验3 中厚样品的速度峰值比薄样品的高，这可能是由于冲击波引起样品中有部分化学反应发生。为了避免样品中形成冲击波，减小HMX 晶体样品厚度，实验4～6 中样品中都没有形成冲击波。

基于考虑阻抗失配修正的迭代Lagrange 数据处理方法，完成了实验1 和实验3 两发实验的数据分析，获得了（011）和（010）两个晶向HMX 晶体的压力-相对比容和声速-粒子速度曲线。（011）和（010）晶向HMX 基于Hugoniot 关系拟合的声速-粒子速度关系分别为us=2.728+2.234up和us=2.756+2.249 up。由于（011）和（010）两个晶向的p-V/V0关系参数基本一致，图中只给出（011）晶向的结果。静压实验结果[23-24]、LASL 冲击实验数据[25]、准等熵加载实验结果[26]、苏锐等[27]采用分子动力学的计算结果和本文中结果见图8，本文工作结果与Yoo 等[23]的静高压实验、文献[25]、Daniel 等[26]的准等熵实验以及文献[27]中的计算结果基本吻合，说明15 GPa 压力范围内未反应HMX 晶体的等温线、准等熵和冲击Hugoniot 线在压力-相对比容热力学平面未完全分离。

表 1 实验条件Table 1 Experimental condition

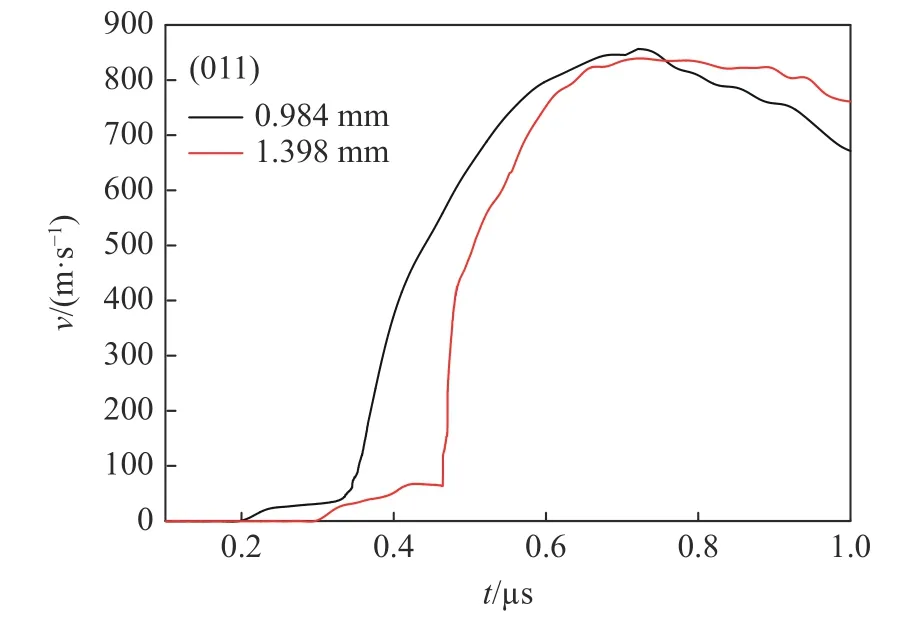
图 2 实验1 的速度响应曲线Fig. 2 Velocity profiles in experiment 1

图 3 实验2 的速度响应曲线Fig. 3 Velocity profiles in experiment 2

图 4 实验3 的速度响应曲线Fig. 4 Velocity profiles in experiment 3

图 5 实验4 的速度响应曲线Fig. 5 Velocity profiles in experiment 4

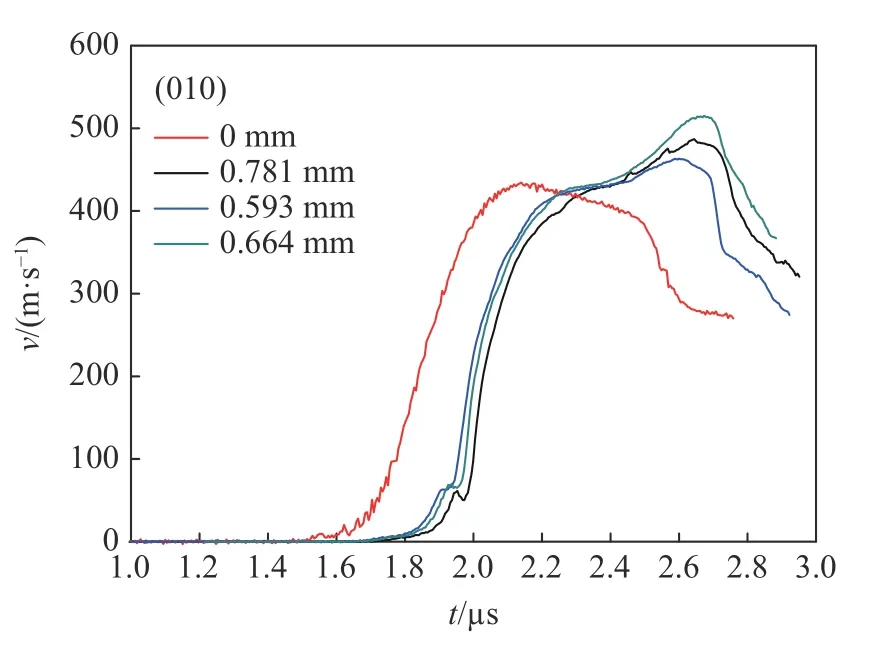
图 6 实验5 速度响应曲线Fig. 6 Velocity profiles in experiment 5

图 7 实验6 的速度响应曲线Fig. 7 Velocity profiles in experiment 6

斜波加载实验对应样品一个连续的压缩过程，每发实验结果进行处理可获得压力峰值内连续变化的声速曲线，（011）和（010）晶向HMX 晶体的拉氏声速曲线见图9。由实验1 获得了(011)晶向HMX 塑性段的拉氏声速-粒子速度曲线（图9（a）），线性拟合得到线性关系为cL=2.728+2×2.234up。由实验6 获得了(011) 晶向HMX 塑性段线性关系为cL=2.765+2×2.226up。由实验4 获得了(010)晶向HMX 弹性段和塑性段的拉氏声速-粒子速度曲线（图9（b）），线性拟合得到弹性段线性关系为cL=3.022+15.867up，塑性段线性关系为cL=2.756+2×2.249up。由实验2获得了(010)晶向HMX 塑性段线性关系为cL=2.713+2×2.255up。由实验3 获得了(010)晶向HMX 塑性段线性关系为cL=2.713+2×2.255up。由实验4 获得了(010)晶向HMX 塑性段线性关系为cL=2.741+2×2.242up。文献[28]对本文中的实验技术和数据处理不确定度进行了研究，实验得到的拉氏声速不确定度为1.5%。

图 8 p-V/V0 曲线与文献数据结果Fig. 8 p-V/V0 curve and literature data

图 9 Lagrange 声速与粒子速度关系曲线Fig. 9 Lagrange sound speed-particle velocity

由界面连续性条件可得，HMX 样品与LiF窗口界面处的粒子速度和应力相等，可用弹塑性转变点处已知物性材料LiF 窗口的应力代替HMX 单晶的应力弹性极限σIEL。表2 所示为本文中实验HMX 晶体的弹塑性转变特征速度、样品厚度和计算的弹性极限。计算时，LiF 单晶物性参数取密度ρ0=2.638 g/cm3，声速c0=5.15 km/s，声速对粒子速度的一阶系数 s=1.35。

图10 为动态加载下HMX 晶体弹性极限与厚度的关系，其中Baeri 等[29]的斜波加载实验数据和Dick 等[18]的冲击加载实验结果作为参考。三方实验数据总体趋势相同：（010）晶向的屈服极限高于（011）晶向的屈服极限；随着样品厚度的增加，HMX 晶体弹性极限出现变化。

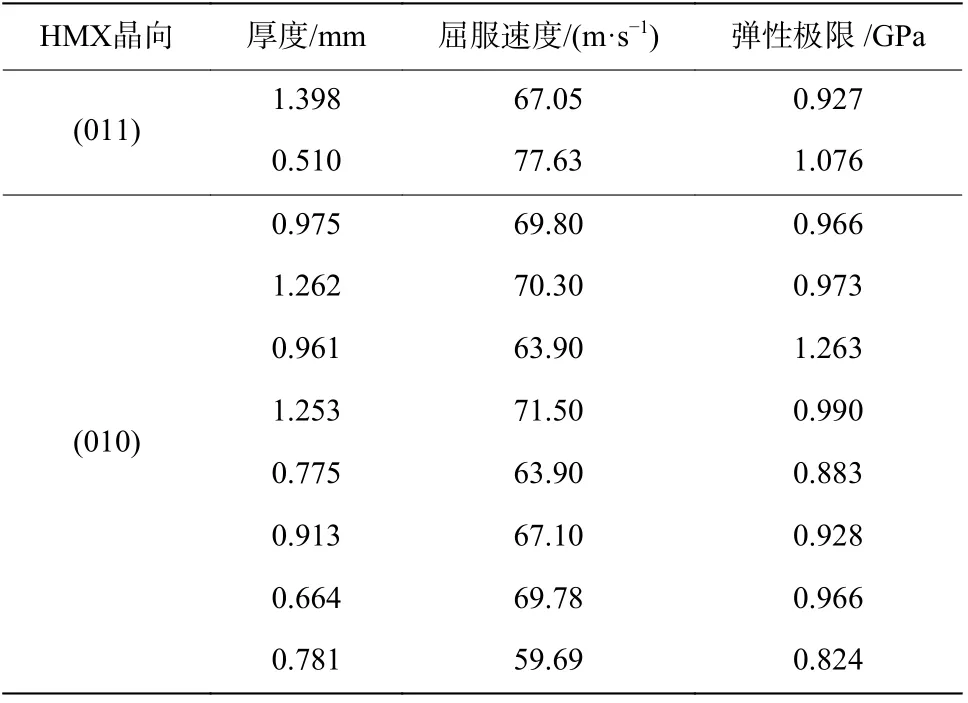
表 2 HMX 晶体的屈服Table 2 Yield of HMX crystals

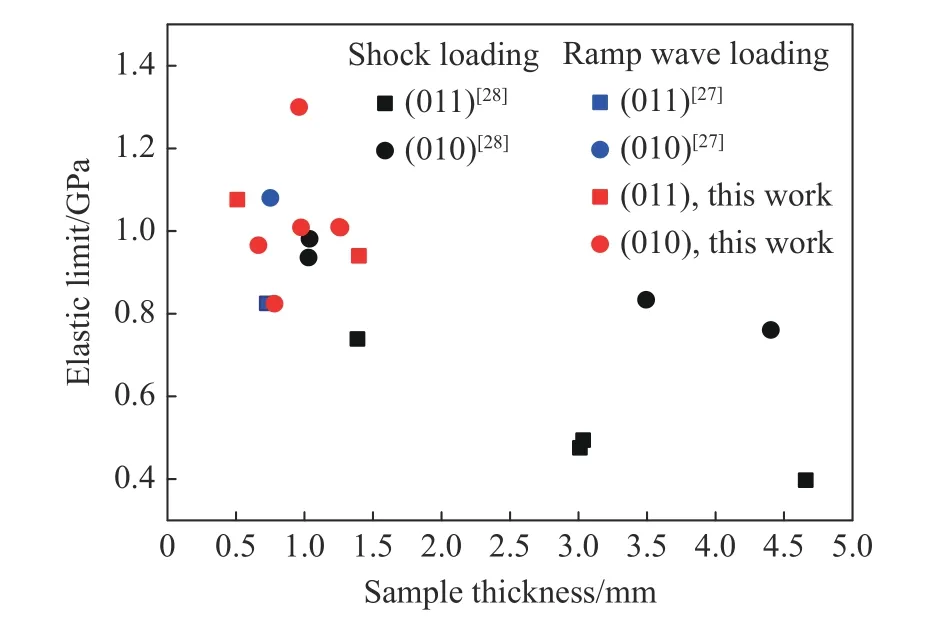
图 10 弹性极限与样品厚度关系Fig. 10 Relationship between elastic limit and sample thickness

2 数值模拟

实验速度波剖面在弹-塑性转变过程中有明显的速度弛豫现象，这是由于有机大分子单晶材料的黏性造成的。为了更好地描述HMX 晶体的斜波压缩物理过程，本文中采用Hobenemser-Prager 本构关系和弹-黏塑性模型[30]，高压物态方程采用适用于等熵热力学过程的三阶Birch-Murnaghan 模型[31]。Hobenemser-Prager 黏弹塑性本构关系的具体形式为：

基于以上物理模型及表3 的模型参数（其中KT0和参考文献[32]并利用本文实验数据对其修正），对HMX 晶体的斜波加载实验过程进行了数值模拟，计算和实验结果如图11～12 所示。这里以Al/LiF 窗口界面粒子速度计算的电极内表面压力历史为输入边界。由图11～12 可得，计算结果与实验结果整体上吻合较好，尤其在弹塑性转变部分，计算结果能较好再现弹塑性区域的速度弛豫现象，说明本文中选择的物理模型及参数适用于HMX 晶体斜波压缩动力学过程的描述。

表 3 模拟计算所用的模型参数Table 3 Model parameters used in simulation

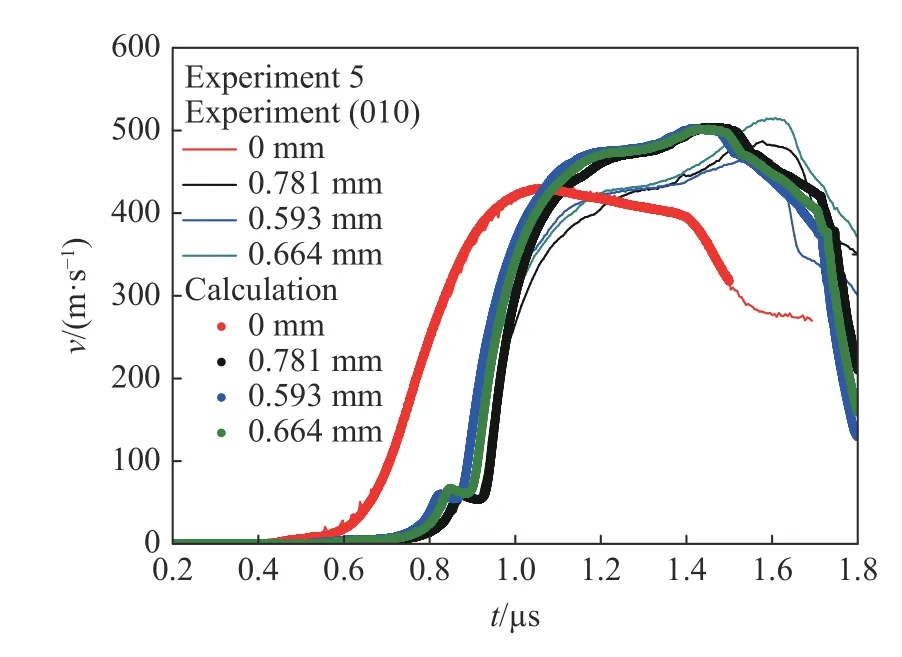
图 11 （010）晶向模拟计算结果与实验结果对比Fig. 11 Calculated and experimental data of (010) crystal direction

图 12 （011）晶向模拟计算结果与实验结果对比Fig. 12 Calculated and experimental data of (011) crystal direction

3 结 论

利用磁驱动加载装置CQ-4 和激光干涉测速技术，开展了15 GPa 压力内两种晶向HMX 晶体的斜波加载实验，获得了包含弹塑性转变信息的速度波剖面。实验结果显示，HMX 晶体两个晶向的动力学参数存在差异，通过数据处理获得了两个晶向HMX 晶体的压力-相对比容曲线和声速-粒子速度曲线。结合Hobenemser-Prager 弹-黏塑性本构关系和三阶Birch-Murnaghan 物态方程对实验过程开展了数值模拟，计算结果可以较好再现HMX 晶体斜波压缩下弹塑性转变对应的速度弛豫过程。

感谢吴刚、邓顺益、税荣杰和胥超等在实验运行和测试方面的帮助。