基于MPC的三电平NPC变流器中点电位控制策略
李君,王倩,李婉婷,施荣,李宁
(1.华北电力大学现代电力研究院,北京 102206;2.西安理工大学电气工程学院,陕西西安710048;3.国网陕西省电力公司经济技术研究院,陕西 西安 710065)
三电平NPC变流器被广泛应用于中高压变频调速、电力系统无功补偿等领域[1]。三电平NPC变流器平均中点电流io为零时,认为其中点电位平衡。但在实际应用中,其中点电位往往会出现低频波动,这有可能会带来器件损耗增大甚至损坏的问题[2]。
近年来,学者们主要针对如何消除其中点电位波动问题提出了一系列改进策略,这些改进策略主要分为硬件控制策略和软件控制策略,其中软件控制策略应用比较广泛。在三电平NPC变流器中,软件控制策略主要研究的是其调制策略[3-4]。三电平NPC变流器的调制策略主要有基于载波正弦脉宽调制(sinusoidal pulse width modulation,SPWM)的中点电位控制方法和基于空间矢量脉宽调制(space vector pulse width modulation,SVPWM)的中点电位控制方法。基于载波SPWM调制的中点电位控制方法主要采用零序电压注入法来解决中点电位波动问题。基于SVPWM调制的中点电位控制方法主要采用调节正负矢量作用时间来消除中点电位波动问题。但不论以上哪种方法,都不能完全实现在全调制度和全功率因数下消除中点电位低频波动[5-7]。
文献[8-10]通过分析SVPWM中各矢量对中点电位和开关频率的影响来控制中位平衡,并尽可能降低开关损耗。文献[11]利用双调制波载波(double modulation wave carrier-based PWM,DMWPWM)调制策略控制中点电位平衡,通过注入合适的零序电压使其在任意调制度、任意功率因数下都可以实现中点电位平衡。但没有推导DMWPWM策略调制波的解析式。文献[12]对单相三电平变换器的网侧电压和直流侧电容电压进行模型预测的数学建模,通过建立代价函数选择适当的开关矢量,控制直流侧上下两电容充放电,实现中点电位平衡。文献[13]提出了一种基于李雅普诺夫的模型预测控制,有效提高ANPC逆变器控制器的运算速率和稳定性,并且可以平衡直流侧电压。
DMWPWM策略虽然可以解决中点电位平衡的问题,但该调制策略开关损耗较大,效率低。相比传统SPWM策略,其开关频率提高了1/3,所以开关损耗增加。针对此种不足,文章提出了一种效率优化的三电平NPC变流器的调制策略,将调制波分成两组,将DMWPWM策略中不等于载波边界值的部分尽可能等于载波边界值;加入模型预测控制,当研究最优控制问题时,所得的最优控制是继电型控制,也即所得的最优控制在两个边界值之间来回转换,称其为Bangbang控制,为防止Bangbang控制对中点电位向前预测两拍,更好的控制中点电位平衡,提出新型控制策略可兼顾三电平NPC变流器中点电位平衡和提高效率减少损耗两个方面。仿真结果验证了其可行性与有效性。
1 DMWPWM策略的基本原理
图1为三电平NPC变流器的主拓扑图。

图1 三电平NPC变流器主拓扑图Fig.1 Main topology of a three-level NPC converter
图1中,Udc为直流侧电压;C1,C2为两个直流侧电容(C1=C2);Ua,Ub,Uc为输出三相电压。DMWPWM策略其中一组连续调制波的解析式为

式中:Uxp,Uxn(x=a,b,c)分别为 DMWPWM 策略上、下两个调制波;Ux为传统SPWM策略调制波;Umin和Umax为Ux的最小和最大值。
图2为DMWPWM策略在调制度m=1.154 7时a相调制波的波形图。由图2可知,采用DMWPWM策略时,一些区域未达到最值,导致该策略的开关频率较大,相比传统SPWM策略,该调制策略的开关损耗增大了1/3。具体解析式推导过程见文献[14],此处不做过多赘述。

图2 DMWPWM策略调制波波形Fig.2 DMWPWM strategy modulation wave waveforms
2 效率优化调制策略
2.1 效率优化调制策略基本原理
效率优化调制策略的基本原则是:通过引入奇数周期DMWPWM策略+偶数周期DMWPWM策略构成效率优化调制策略,使调制波尽可能为其最值的方式来降低系统开关损耗,由此推导出效率优化调制策略调制波的解析解。
效率优化调制策略将DMWPWM策略的上调制波Uxp分为Uxp1和Uxp2;将下调制波Uxn分为Uxn1和Uxn2。由此可得到效率优化调制策略和DMWPWM策略调制波的关系式为

此时,Uxpimax=-Uxnimin(i=1,2)。
2.2 效率优化调制策略调制波的解析式
不同调制度范围内,在DMWPWM调制波中注入不同的零序电压,得到效率优化调制策略的调制波解析式如下。
当ωt∈[iπ/3,(i+1)π/3]、调制度m∈(0.666 7,1.154 7]及DMWPWM策略的调制波不等于载波边界值时,在DMWPWM调制波中注入零序电压Uo=1-Umax,得到效率优化策略上、下两组调制波的表达式为

同理,当调制度 m∈(0.577 4,0.666 7]和 m∈(0,0.577 4]时,在DMWPWM调制波不等于载波边界值时,DMWPWM调制波中分别注入零序电压Uo=1-Umax和Uo=Umax,具体推导过程详见文献[15],此处不作过多介绍。
根据效率优化策略调制波的解析式,可得到不同调制度时调制波的波形图如图3所示。

图3 效率优化策略调制波波形图Fig.3 Modulation waveforms diagram of efficiency optimization strategy
3 基于MPC的中点电位控制策略
当单独应用式(2)中的第一组或第二组调制波时,三电平NPC变流器中点电位初始值会向下或向上偏移,本文引入模型预测控制(MPC)策略实时切换两组调制波来实现中点电位平衡。针对效率优化调制策略对硬件参数较为敏感的问题,模型预测控制通过预测两拍的中点电位状态可在效率优化调制策略的两组调制波中选择一组合适的调制波,从而控制中点电位平衡。
3.1 MPC中点电位控制策略基本原理
由基尔霍夫电压定律推导出三电平NPC变流器各相输出电压的表达式为

式中:usx,ux(x=a,b,c)分别为三相电网电压和变流器输出电压;ix为入网电流;R,L分别为平波电抗器的等效电阻和电感;uN为三相共模电压。
对于三电平NPC变流器而言,假设一个开关周期用Ts来表示,由欧拉公式可得到其入网电流的离散表达式:
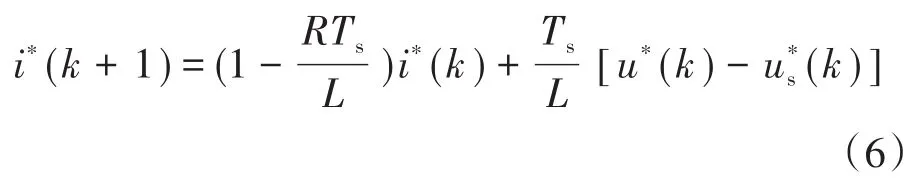
式中:i*(k+1),i*(k)分别为入网电流的第(k+1)个周期值和第k个周期值;u*(k),u*s(k)分别为第k个周期的变流器输出电压和电网电压。
使用欧拉算法将直流侧电容电压进行离散化可以得到中点电位在下一刻时的表达式为

式中:Uc1(k+1),Uc2(k+1)分别为第(k+1)个周期的两电容电压;Uc1(k),Uc2(k),i1(k),i2(k)分别为第k个周期的两电容电压和电流。
将式(1)~式(3)代入式(7),可得到用中点电流来表达直流侧电容电压的离散化公式:

由此可得中点电位的表达式为

由式(9)可预测到下一时刻的中点电位的值,同理可推导出再下一时刻三电平NPC变流器的输出线电流和电容电压的表达式:
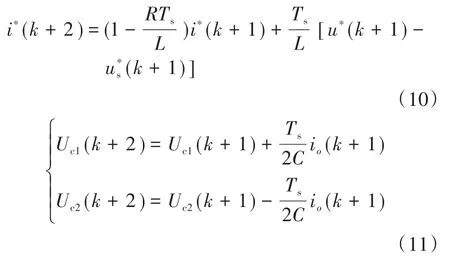
由此可得中点电位的表达式为
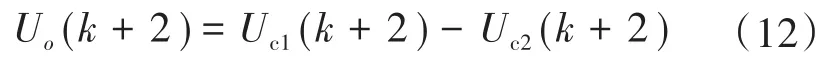
在效率优化调制策略的基础上加入预测控制的最终目的是选择一组合适的调制波。
3.2 MPC中点电位控制策略流程
图4为MPC中点电位控制策略的流程框图。

图4 MPC中点电位流程框图Fig.4 MPC midpoint potential flow diagram
由图4流程图可以看出应用模型预测可以控制中点电位的原因是:为防止中点电位的Bangbang控制,应用模型预测判断两拍的中点电位来选择合适的一组调制波。由上面推导可得到(k+1)个周期和(k+2)个周期时刻的中点电位,将Uo(k+1)和Uo(k+2)分别与参考电压Uref比较,用比较的结果来选择恰当的一组调制波,将Uo(k+1)与Uref比较,其比较过程如下:
1)如果Uo(k+1)≤Uref,则选择当前组的调制波,不需切换调制波,否则切换为另一组,然后将Uo(k+2)与Uref比较。
2)如果Uo(k+2)≤Uref,则不需切换调制波,继续为当前组,否则切换为另一组调制波。
也就是说,必须Uo(k+1)≤Uref和Uo(k+2)≤Uref同时满足时不需切换调制波,否则,只要有一个不满足条件就需将调制波切换为另外一组。
4 仿真与实验结果分析
4.1 仿真验证
在Matlab/Simulink中搭建MPC中点电位控制模型,仿真参数为:直流母线电压500 V,直流母线侧电容2 500 μF,基波频率50 Hz,开关频率3 kHz,滤波器电感10 mH,滤波电容1 μF。
图5为未加MPC时效率优化调制策略(C1≠C2)中点电位的仿真波形图(m=1.154 7)。可以看出由于效率优化调制策略的前提条件过于理想,当直流侧的电容容值不相等时,随着运行时间的增加,中点电位将逐渐偏离其参考值。

图5 未加中点电位控制策略的仿真波形(C1≠C2,m=1.154 7)Fig.5 Simulation waveform without midpoint potential control(C1≠C2,m=1.154 7)
图6为m=1.154 7 MPC中点电位控制策略的输出线电压Uab、输出三相电流iabc以及中点电位的波形。由图6可知,采用MPC中点电位控制策略,中点电位可实现平衡。
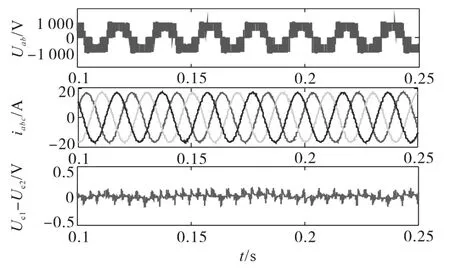
图6 MPC效率优化控制策略的仿真波形(m=1.154 7)Fig.6 Simulation waveforms of MPC efficiency optimization control strategy(m=1.154 7)
图7与表1分别为MPC中点电位控制策略、DMWPWM策略和效率优化策略这三种策略的输出相电压THDUa对比图和表。由图7可知,在低调制度时,MPC中点电位控制策略的THDUa比DMWPWM策略小。随着调制度的增加,THDUa逐渐增大,但在相同调制度下,MPC中点电位控制策略的THDUa比DMWPWM策略的THDUa较大,但差距不大。由于MPC中点电位控制的开关频率不固定,导致输出电压的谐波含量不固定,所以不同调制度的THD趋势与DMWPWM策略不同。MPC中点电位控制策略与效率优化调制策略的THDUa相差不多。由表1可知,当m=1.154 7时,效率优化调制策略的THDUa为67.86%,MPC中点电位控制策略的THDUa为67.5%,两种策略的THDUa基本相等,三种策略中,DMWPWM的THDUa最小,等于65.79%。三种策略THDUa对比结果为:DMWPWM策略<MPC中点电位控制策略<效率优化调制策略。

图7 三种策略THDUa(%)对比图Fig.7 THDUa(%)comparison figure of three strategies
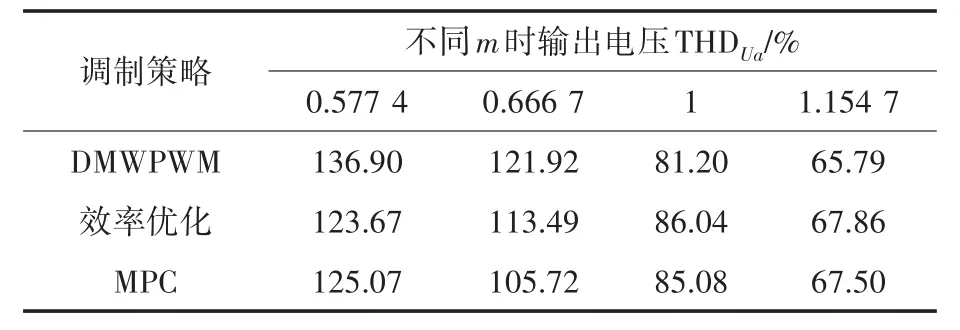
表1 三种策略THDUa(%)对比表Tab.1THDUa(%)comparison table of three strategies
图 8为当 C1≠C2时,m=1.154 7时,加入模型预测后效率优化调制策略的中点电位波形图,由此可知,加入闭环控制后两直流电容容值不同时,中点电位依然可以保持平衡。此中点电位模型预测控制可解决由硬件引起的中点电位偏移问题。
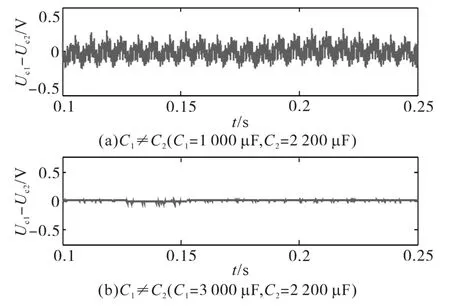
图8 效率优化控制策略中点电位波形(C1≠C2,m=1.154 7)Fig.8 Neutral potential waveforms of efficiency optimized control strategy(C1≠C2,m=1.154 7)
4.2 实验验证
在三电平NPC逆变器实验平台上进行MPC中点电位控制实验。实验平台参数为:直流侧电压电压Udc=650 V;开关频率fs=10 kHz;滤波电容Cf=20 μF;直流侧电容 1 000 μF;滤波电感 Lf=50 μH;调制度ms=0.8,0.7,0.6;采样时间Ts=0.000 2 s。
4.2.1 并网运行时MPC中点电位控制输出特性
图9为当负载从0变到40 kW时,即从空载到满负荷(40 kW)时,逆变器的输出相电流Ia,Ib和两直流侧电容电压Uc1与Uc2的波形图。

图9 效率优化调制策略并网实验结果(ms=0.8)Fig.9 Experimental results of grid-connected efficiency optimization modulation strategy(ms=0.8)
图9a,图9e,图9f分别为t1时刻负载从0 kW→5 kW,t2时刻负载从30 kW→20 kW,t3时刻负载从30 kW→40 kW时的输出波形图,可以看出直流电容电压在动态变化后依然可以保持平衡,幅值基本在325 V左右波动,随时间推移,两直流侧电容电压保持平衡,这与理论分析一致。输出相电流稍微畸变后幅值分别从8 A→12 A,18 A→15 A,18 A→21 A,输出仍为正弦。图9b,图9c,图9d,图9g分别为负载为10 kW,20 kW,30 kW和40 kW时的并网输出波形,可以看出在不同负载情况下,三电平NPC逆变器的中点电位都可以保持平衡,说明所提出的MPC中点电位控制是有效的。
4.2.2 MPC中点电位控制的系统效率验证
在三电平NPC逆变器的并网实验中,对MPC中点电位控制策略进行效率分析,测量并网三电平逆变器应用MPC中点电位控制策略从10%负载到100%负载时的系统效率,将DMWPWM策略、效率优化策略、基于MPC中点电位控制策略的系统效率进行对比,如表2所示。

表2 三种策略系统效率对比表Tab.2 Systematic efficiency comparison table of three strategies
由表2可以看出,MPC中点电位控制策略与其他两种策略相同,都是在30%负载附近时系统效率最高,此时系统效率为98.866%,效率优化开环策略30%负载时的效率为99.027%,开环策略与闭环策略的效率相差0.161%。由于加入MPC后效率优化策略的开关频率不固定,在10%到100%负载附近其效率都比效率优化策略小,但比DMWPWM策略大。由于效率优化策略属于开环控制,其开关频率只受调制策略的影响,开关频率基本固定,开关损耗固定。但在效率策略中加入中点电位闭环控制时,由于在选择两组调制波时是根据当前时刻中点电位的偏移情况适时选择,不是规律选择,导致开关频率不固定,比效率优化开关频率大,所以其开关损耗也比效率优化策略的开关损耗大,效率较低。
为了更清楚地研究三种策略的效率,将DMWPWM策略、效率优化调制策略、MPC中点电位控制策略从10%负载到100%负载时的系统效率进行统计,得到三种调制策略的系统效率对比图,如图10所示。

图10 三种策略的系统效率对比Fig.10 Systematic efficiency comparison of three strategies
由图10可知,三种策略的效率最大都在30%负载附近,效率曲线趋势大致相同,系统效率的高低排序为:效率优化调制策略>中点电位控制策略>DMWPWM策略,整体趋势都是先增加后逐渐减小。虽然中点电位控制策略的系统效率比效率优化开环策略的效率略低,但其效率也普遍在97%以上,基本满足效率要求。
5 结论
文章通过详细推导MPC中点电位的基本算法,将效率优化策略与MPC相结合,控制了中点电位平衡。
主要结论有:当C1≠C2时,效率优化调制策略的中点电位偏移,说明效率优化策略中加入中点电位控制是有必要的。上下两电容容值不等的情况下,MPC中点电位控制策略依然可以实现中点电位平衡。将三种策略的输出电压THD进行对比,MPC中点电位控制策略输出电压THD最小,说明中点电位控制策略有利于改善输出波形质量。在三电平NPC逆变器并网实验中对MPC中点电位控制策略进行验证。结果表明该方法可在不同调制度下(m=0.6,0.7,0.8)达到调制的目的,负载从0~40 kW变化时,直流侧电容电压可以保持平衡;将三种策略在10%到100%负载范围的系统效率进行对比,可看出三种策略的系统效率都在30%负载附近时达到最大。MPC中点电位控制策略的系统效率在DMWPWM策略与效率优化策略之间,系统效率都在97%以上,可达到基本要求。
仿真与实验证明,MPC中点电位控制策略可解决由非调制因素引起的中点电位偏移问题,该方法弥补了效率优化策略的不足,为解决三电平NPC变流器的中点电位偏移问题提供了一种新策略,有利于三电平NPC变流器的广泛应用和发展。

