滑雪场积雪模拟研究进展
邓 婕, 车 涛
(1.中国科学院西北生态环境资源研究院甘肃省遥感重点实验室黑河遥感试验研究站,甘肃 兰州 730000;2.中国科学院大学,北京 100049)
0 引言
滑雪作为一种主要的冬季运动和冬季旅游活动,可以创造巨大的商业机会,进而促进区域经济的发展[1-2]。在一些地区,滑雪旅游产业是其重要的经济来源,比传统的农业和工业带来的收入更多[3]。滑雪旅游的发展为山区居民的就业打开了新的大门,带去了可观的经济收入,促进了当地社会和经济的发展[4-5]。2022 年冬奥会的成功申办极大地促进了中国冬季体育产业的发展[6]。中国政府向国际奥委会承诺:到2022 年,将带动3 亿人参与冰雪运动。美国、奥地利、日本等传统的滑雪旅游市场已趋于饱和,而中国作为一个快速增长的市场,滑雪场的数量从2010 年的270 家急剧增加到2019 年的770家[7]。
作为一个依赖于雪的行业,滑雪旅游因其对气候变化极为敏感而得到了广泛关注[8-10],这些研究的重点是未来自然积雪资源和人工造雪条件的变化对滑雪季节长度的影响[11-15]。积雪条件是评价滑雪场盈利能力的关键指标[16],通过积雪模型准确地模拟滑雪场积雪对评估气候变化影响下滑雪旅游目的地的脆弱性是十分重要的[17]。
滑雪场的积雪模拟与自然积雪模拟不尽相同,滑雪场地积雪的人工管理使雪道上的积雪与自然积雪属性(如雪密度、雪比表面积等)相差较大[18]。雪道的人工管理主要包括人工造雪和雪道维护。人工造雪可以弥补自然积雪的不足,是滑雪产业不可或缺的组成部分[19]。雪道维护是指雪道上的积雪需要进行人工处理(如压雪、平整雪道等)使其达到滑雪运动的标准,如赛道用雪密度不低于500 kg·m-3[18,20]。因此,对滑雪场积雪进行模拟时需将自然积雪模型与雪道人工管理模型相结合。
为明晰近年来滑雪场积雪模拟研究取得的进展,本文总结了滑雪场积雪模拟研究的发展趋势,归纳了关键的模拟方法,进一步分析了我国滑雪场积雪模拟研究的关键问题以及有待进一步开展工作的领域。
1 滑雪场积雪模拟的发展
20世纪80年代末,连续几个积雪条件恶劣的冬天之后,引起了气候变化对滑雪产业影响的科学研究[21-23]。这一阶段的研究主要基于国家或区域尺度,采用经验模型分析与滑雪季节长度相关的多个气象变量之间的统计关系[13]。Breiling 等[24]利用1965—1995 年气象台站数据分析了奥地利范围内的气温、降水量和雪深之间的统计关系。根据所建立的统计关系预估了未来气温升高2 ℃时的雪深,结果显示用于评估滑雪旅游积雪可靠性的雪线将向上移动105~200 m。
早期应用在滑雪旅游目的地的物理融雪模型较为简单[25-26]。最早使用的物理模型中,计算降雪和融雪所需的气候输入参数只有月平均气温、月平均降水量和日平均气温的标准差[25]。该模型对滑雪场地积雪可靠性的评估存在着几个问题。首先,融雪模型将雪深大于1 cm 或2 cm 的天数定义为可滑雪日数。然而,在1~2 cm 的积雪上滑雪是不可能的。其次,该模型计算全年的可滑雪日数,而不考虑特定的积雪覆盖日是否处于滑雪季节之内。1990 年和1992 年,当澳大利亚滑雪场在10 月初停止营业之后,部分滑雪场所在地区仍然存在积雪,这些问题会导致对潜在可滑雪日数的高估。因此,之后的模型只考虑滑雪季节的积雪条件,且将雪深设定为滑雪场实际可运营的阈值,如在滑雪季节滑雪场的雪深大于30 cm 的日数达到100 天即可盈利[27]。然而,这些研究的一个重要局限是完全没有考虑人工造雪[28-31],而不考虑人工造雪将会导致对滑雪场可滑雪日数的低估。
近十多年来,随着人工造雪技术的迅速普及,人工造雪对滑雪场的运营起到了非常重要的作用,仅利用自然积雪条件来评估滑雪场的积雪可靠性受到了质疑[17]。Scott 等[11]开发的SkiSim 模型是第一个包含人工造雪的积雪模型,采用了较为简单的度日模型进行单点尺度的积雪模拟,不考虑雪层物理性质。最新的SkiSim 版本中将单点模拟发展为半分布式模拟,改进了造雪模块的造雪规则,以更好地提出整个滑雪季节中人工造雪的管理模式[13]。Pons 等[32]利用单层能量平衡融雪模型和SkiSim 模型对未来冬季气温升高2 ℃和4 ℃情景下滑雪场的自然雪深和人工造雪潜力进行了模拟。与此同时,也有一部分模型将自然积雪和人工造雪分开考虑[15,33-34]。虽然其中一些模型对造雪潜力的模拟是稳健的,即拥有逐小时的分辨率且考虑了对造雪有着重要影响的空气湿度,但对自然雪深和造雪潜力的单独分析不能对融雪量和雪深进行综合计算[12,14,35-36]。如Hendrik等[33]在模型中只考虑了自然积雪的消融,没有考虑人造雪的消融。评估结果总体显示,人工造雪减弱了气候变化对滑雪旅游的影响。在未来更温暖的条件下,滑雪场对人造雪的需求会大大增加[17]。
这些人工造雪模拟方法大多是基于点或者半分布式(在垂直海拔上)的模拟,通常只模拟了滑雪场平均海拔高度的积雪条件[11,13,32,36-37]。Pons-Pons等[38]使用了研究区的最低海拔和最高海拔,而Hennessy等[39]将滑雪场视作一个单点或在滑雪场最高、中间和最低海拔上进行模拟。这些对滑雪旅游目的地积雪条件的评估得出的是可靠或不可靠的二元结论,且对雪道维护的处理相对粗糙。近几年,一些研究在基于物理的、空间分布的积雪模型中输出明确量化的人造雪,在网格尺度上模拟和预估滑雪场的积雪条件[40-41]。分布式模型考虑了滑雪场的地形条件和设施条件,对雪道维护的处理亦更为细致。
国内的研究主要集中在对区域滑雪旅游气候条件的分析与评估[42-44]。如,Cai等[42]以积雪资源和天气条件为基础,建立表征冬季旅游资源的积雪丰富度和气象适宜度指标,分析了吉林省冬季旅游目的地的空间适宜性。Fang 等[45]应用SkiSim 2.0 模型预估了我国116个滑雪场未来的积雪条件以评估其气候风险。
2 模拟方法
滑雪场的积雪条件需要在适当的时间得到很好的控制,雪道的积雪要平整、均匀、结实,足以承受常规数量的滑雪者的影响[46-47]。自然降雪量通常是高度可变的。出于对滑雪场运营的及时规划以及对有效管理雪道滑雪条件的需求,在过去的几十年里,世界各地的滑雪场越来越依赖于造雪设施来弥补自然积雪的不足。滑雪场地的积雪由自然积雪和人造雪组成。对滑雪场地积雪的模拟需要同时考虑两种不同性质的积雪以及雪道的人工维护,通过耦合自然积雪模块与雪道人工管理模块计算滑雪季的长度,从而实现对未来滑雪季节长度更真实的预估(图1)。依据自然积雪模拟方法和雪道人工管理(人工造雪的规则和雪道维护)的不同,应用于滑雪场的积雪模拟方法可以简单的分为两类:单点或半分布式模拟和分布式模拟。
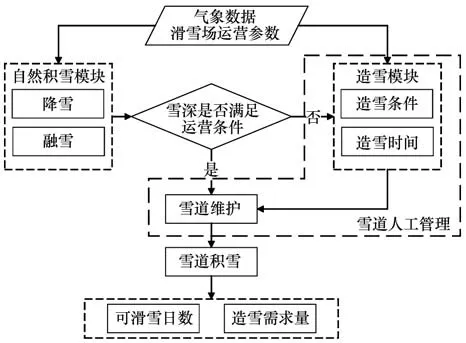
图1 滑雪场积雪模拟框架Fig.1 Methodological framework of simulation of snowpack in ski resorts
2.1 单点或半分布式模拟
单点模拟,即将每个具体的滑雪场作为一个点进行研究,该点的位置一般取该滑雪场的平均海拔高度或最低海拔高度,或计算在最高、最低和中间海拔输出结果的平均值[11-12,48-49]。由于滑雪场海拔最低的区域具有最少的积雪,这些地点的结果可以被视为每个滑雪场的最坏情况[50]。为了更精确地反映滑雪场不同海拔区域积雪条件的变化情况,一些研究采用半分布式模拟的方法,等间隔地选取了滑雪场多个海拔带进行模拟[13,33,51]。通常,半分布式模型在每个滑雪场最终输出一个平均结果[52]。常用于单点或半分布式模拟的模型为简化的能量平衡模型(如,单层、双层的能量平衡融雪模型)和基于度日因子的概念模型(表1)。

表1 滑雪场积雪模拟方法比较Table 1 Comparison and summary of simulation methods of snowpack in ski resorts
能量平衡模型考虑了积雪界面的能量交换。单层融雪模型是指将积雪层作为一个整体,计算整个积雪层的融雪量[53]。在单层的能量平衡融雪模型中,积雪具有特定性质,如高反照率、低热容量和低导热系数,雪密度通常是固定的。尽管单层能量平衡融雪模型在表征雪的物理性质方面存在缺陷,但由于其参数相对较少,通常用于将滑雪场视为单点的模拟。例如,Pons 等[32]、Pons-Pons 等[38]使用的GRENBLS(Ground Energy Balance for Natural Surfaces)模 型。Wobus 等[49]利 用UEB(Utah Energy Balance)模型模拟了美国247 个滑雪场的自然积雪,而人工造雪则以潜在的造雪时间(小时)来评估。双层能量平衡融雪模型则将积雪层分为两个部分,一层为表面固定厚度的雪层,另一层为下积雪层,上层接受辐射热通量和感热、潜热控制,下层考虑雪层的密度、液态水含量等物理属性。Gilaberte-Búrdalo 等[36]使用了双层的能量平衡融雪模型——ISNOBAL 模型[54]模拟滑雪场的自然积雪,但该研究以潜在的造雪时间作为代理指标衡量人工造雪的能力,没有计算具体的人工造雪量。
度日模型可以看作一种特殊的单层融雪模型,以积雪消融与正积温的线性关系为基础,反映了单位正积温产生的积雪消融量。度日模型因其简单易用且性能卓越而被广泛应用于滑雪场积雪模拟。例如,Hendrik 等[33,50]使用了Clark 等[55]发展的度日模型评估了新西兰和澳大利亚滑雪场的积雪条件。Hennessy等[12]利用Whetton等[56]发展的CSIRO度日模型模拟得到研究区2.5 km×2.5 km分辨率的自然雪深,该研究区包含多个滑雪场,将每个滑雪场视为一个单点,然后计算滑雪场所在位置除去自然积雪后所需人工造雪量。SkiSim 2.0模型[13]是目前滑雪场积雪条件评估研究中应用最广泛的半分布式度日模型。该模型在间隔100 m 的海拔带进行模拟,最终输出单个滑雪场的平均结果。SkiSim 2.0模型所需的输入包括日最高气温、日最低气温和日降水量,应用时需要对度日因子、固态降水与液态降水的空气温度阈值进行参数率定。
单点或半分布式模型通常包含一个简单的造雪模块,该模块使用简化的假设处理造雪规则和雪道维护(表2),模拟的滑雪季节长度是通过在单点或每个海拔带的自然积雪上添加人造雪来实现的。目前,使用最广泛的滑雪场积雪可靠性评判标准为:在滑雪季节,雪深大于30 cm 的日子被称为可滑雪日,可滑雪日达到100天才能盈利,没有达到此标准的滑雪场则被认为是积雪不达标的[11,57]。依据积雪可靠性评判标准,模型制定相应的规则来实施造雪的操作决策。模型只模拟一年中定义为滑雪季节的日期,如Fang等[45]在评估我国滑雪场积雪条件时使用的时间段为12 月15 日至次年4 月1 日。在此期间,当雪道雪深小于30 cm 且环境条件符合造雪要求时,造雪模块将会被激活。根据滑雪场技术人员的经验,气温低于-5 ℃时可进行人工造雪操作[13],或以日最低气温低于-2 ℃时作为潜在造雪日[32]。假设每个滑雪场均拥有当前最先进的造雪系统[11],造雪机覆盖滑雪场所有雪道且均匀地分布在每条雪道上,则在潜在的造雪日中,每天最多能产生10 cm 的积雪。此外,SkiSim 2.0 模型[13]中规定:在滑雪季开始之前,不论自然积雪的深度是否满足运营需求,均使用人工造雪在雪道上建立30 cm的基础层,以确保滑雪场在预定日期营业[58]。

表2 SkiSim 2.0模型中造雪模块参数Table 2 The parameters of snowmaking module in SkiSim 2.0
单点或半分布式模拟采用简化的融雪模型,输入参数较少且易获取,因此适用于区域间多个滑雪场积雪条件的评估和相互比较。正如上文提到,一些学者认为单点或半分布式模型对具体滑雪场的研究仍然是粗糙的,得出的是达标或不达标的二元结论[41]。考虑到地形条件对积雪产生较大的影响,单点或半分布式模型限制了对滑雪场内部积雪条件的分析。此外,模型中使用造雪模块简化雪道人工管理过程。例如,将雪道上的积雪密度设定为350 kg·m-3,以此来模拟压雪、平整雪道等雪道维护的作用,但是这些简化的处理方法不能定量计算人工造雪量和需水量[13]。
2.2 分布式模拟
分布式模型在网格或雪道上划分出来的小单元尺度上对滑雪场积雪进行模拟,能够捕捉到地形起伏、坡度和曲率等变化对积雪的影响,更细致地考虑了人工造雪的操作和雪道维护(表1)。模型的时间分辨率通常为逐小时,空间分辨率精确到几十米甚至几米,因此在模拟滑雪场积雪条件时,需要对模型驱动数据进行降尺度处理。
滑雪场分布式积雪模拟研究中多使用精细的多层能量平衡模型,其与单层、双层能量平衡融雪模型的主要区别在于对积雪内部属性以及相关物理过程的描述和参数化方案的不同。多层能量平衡模型尽可能地模拟积雪的垂直分层,如Crocus模型中没有限制最大分层数量,但最少需要3 层以模拟积雪内部热传导[59]。在初始分层确定之后,模型会根据积雪状态自动调整分层,优先考虑表层和底层,以便准确解决雪面-大气、雪层-土壤界面的能量交换。此类模型可以详细描述积雪层的物理属性与雪粒的微观结构随时间演化过程[60-61]。由于输入驱动数据为逐小时分辨率的气温、降水量、相对湿度、风速、太阳辐射等,此类模型很少用于区域或全球积雪模拟[62]。目前,分布式模型已被应用于滑雪场的积雪模拟中,如Crocus 模型[59]、AMUNDSEN 模 型[40]、SNOWPACK Alpine/3D 模型[63]。Hanzer 等[41]使用以上三种模型对阿尔卑斯山9 个滑雪场的积雪进行了模拟,各模型的具体特征见表3。

表3 三种分布式滑雪场模型的结构和输入参数Table 3 The structure and input data of the Crocus、AMUNDSEN、SNOWPACK Alpine/3D models
分布式模型对雪道人工管理的处理较为细致,其中造雪模块同样是在网格或由雪道划分的小单元尺度上进行模拟,并考虑了滑雪场中雪道的具体位置、造雪机的数量和规格以及造雪需水的供给能力等。例如,Marke 等[40]将造雪模块与模块化、基于物理的分布式积雪模型AMUNDSEN 进行耦合,在50 m×50 m 的网格上输出奥地利一个滑雪场的雪深分布结果。该模型使用基于湿球温度的线性函数计算造雪机每小时最大产雪量,当湿球温度低于-2 ℃时满足造雪条件。选择所有达到造雪条件的网格,根据滑雪场的造雪机数量和输水能力,从而计算整个滑雪场的最大产雪量,所得造雪量均匀地分布在所选的雪道网格上。在滑雪季节,该模型将自然积雪与模拟的人工造雪结合起来,使雪道上保持最小雪深为60 cm。该研究假设造雪机均匀地分布在雪道上,并不一定反映滑雪场地的实际条件,但该模型对输入数据要求不高,因此可以推广应用于其他滑雪场。
更复杂的雪道人工管理方法可以考虑每个造雪机的确切位置、滑雪场基础设施和资源的可用性,如造雪机的数量和造雪效率、可用水量以及抽水能力等(表4)[41,47]。此外,模型中还考虑了压雪、修饰等雪道维护过程。基本假设是:将新雪均匀分布于整个雪道,由于滑雪者和风力作用而移动的雪在每天营业结束后都会被处理至原始位置;通过压雪机的压实、平整、打碎雪团及雪面薄冰等维护过程使雪道积雪的各参数达到标准值,如密度为450 kg·m-3、雪比表面积为25 m2·kg-1[18]。
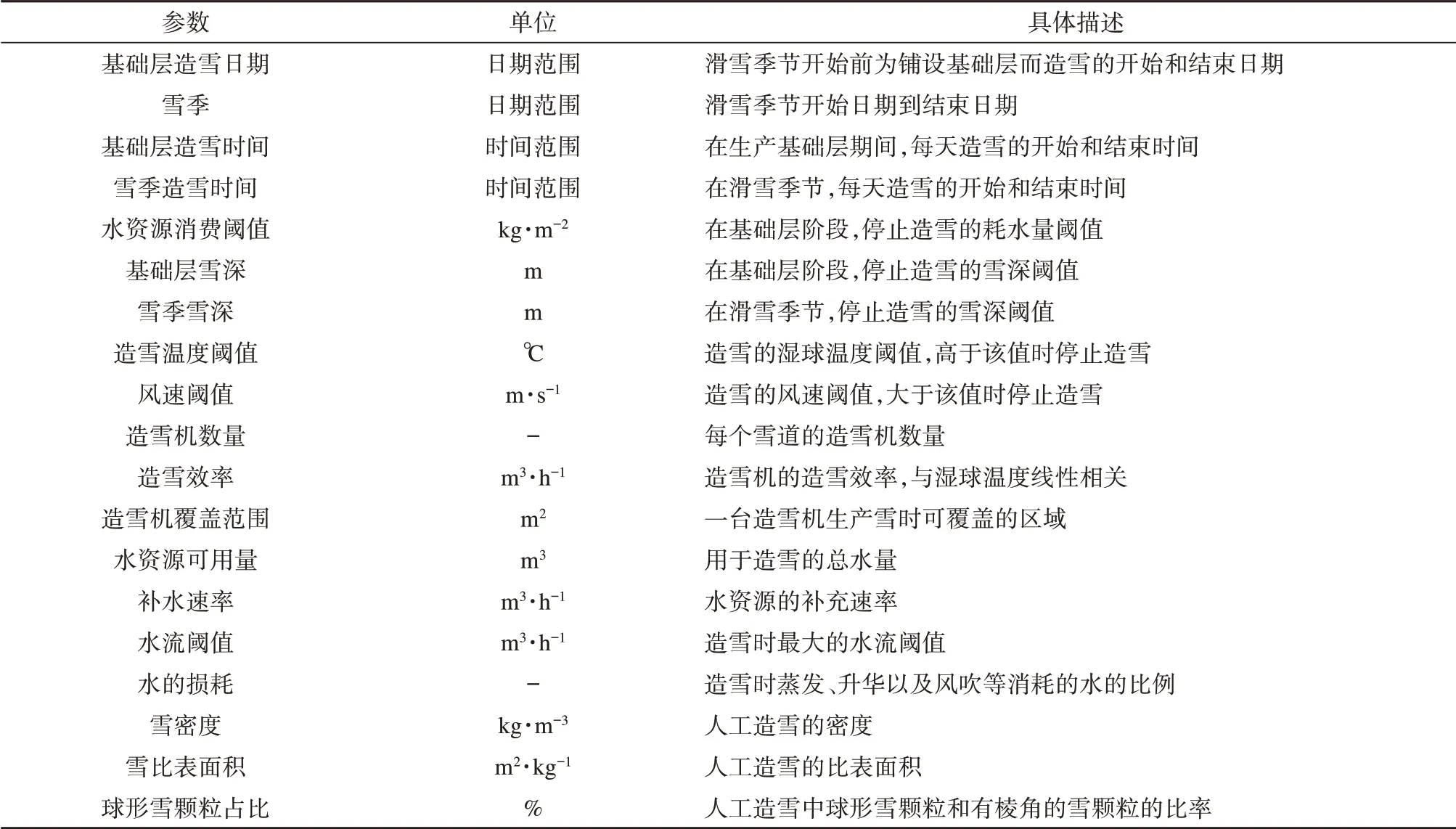
表4 雪道人工管理的参数Table 4 The parameters of snow management
分布式积雪模型可以很好的解决由地形阴影、坡度和坡向等地形效应引起的积雪分布的空间异质性问题,在每个网格单元使用能量平衡法来确定积雪的变化,可以提高滑雪场气候风险的预估精度。然而,分布式模型需要非常精细的气象参数以及滑雪场的设备和操作信息,因此适用于单个或较少数量滑雪场的积雪模拟。
3 中国滑雪场积雪模拟的关键问题
近年来,我国滑雪旅游发展迅速,滑雪场的数量从2010 年的270 家急剧增加到2019 年的770家[7]。滑雪场在我国分布广泛,所处位置的气候差异十分显著。其中,大型、高等级滑雪场主要分布在积雪资源较为丰富的北方。与此同时,我国也是世界上最大的滑雪初学者市场[64]。为了满足初学者的市场需求,在纬度、海拔较低的东部、南部地区,也涌现出大量的小型滑雪场[6]。虽然国际上关于滑雪场积雪模拟的研究非常多,但在我国开展的相关研究相对较少[45]。考虑到我国滑雪场的实际情况,我国滑雪场积雪模拟时应注意以下几点问题。
首先,模型应重点考虑人工造雪。即使在我国东北和西北,雪深都普遍小于欧美主要滑雪胜地(如阿尔卑斯山、落基山脉等),华南、华东等纬度较低的地区积雪更少。自然积雪资源的稀缺使得我国绝大多数滑雪场极大地依赖人工造雪,在一些较低纬度或低海拔地区,滑雪场的积雪完全为人造雪。因此,模型应重点考虑人工造雪,甚至在纬度或海拔较低的滑雪场可以只考虑人工造雪。
其次,需要注意滑雪场雪道人工管理模式的不同。一些在欧美滑雪场广泛应用的规则照搬至我国滑雪场可能会出现较大误差。例如,100 天标准并不适用于我国处在较为温暖、社会经济条件较好地区的滑雪场。通过调查,一些南方的小型滑雪场客流量大、运营成本相对较低,在滑雪季节只需营业60 天即可盈利[6]。此外,为了保证雪道上有充足的积雪,一些滑雪场在白天营业时间会同步进行人工造雪,而欧美滑雪场造雪操作主要在晚上非营业时间进行。白天较高的温度会导致升华现象更为明显,从而降低造雪效率和水的利用率。
4 结语
早期应用于滑雪场的积雪模型只考虑了自然积雪。全球变暖使得滑雪场越来越依赖人工造雪,近几年的研究更多地考虑到人工造雪和雪道的维护过程。将滑雪场视为单点进行积雪模拟相对较为简单,将基于度日因子的概念模型或简化的能量平衡模型与造雪模块进行耦合,可以对不同区域中多个滑雪场进行评估和对比分析。进一步考虑地形因子和滑雪场设施条件,分布式能量平衡模型在网格或由雪道划分出来的小单元尺度上模拟滑雪场地的积雪,能够输出定量的人造雪产量。
通过对人工造雪的定量模拟,同时考虑水资源和能源的消耗,可以综合评估滑雪场的气候风险管理能力。目前,应用在滑雪场的分布式积雪模型较为复杂,主要是多层能量平衡模型。考虑到对滑雪场积雪进行模拟时不需要非常详细地描述雪层内部物理过程,简化的分布式融雪模型更适合用于滑雪场的积雪模拟。

