Delta distribution of electronegative plasma predicted by reformed“spring oscillator”dynamic equation with dispersing force

Shu-Xia Zhao(赵书霞) and Jing-Ze Li(李京泽)

Key Laboratory of Materials Modification by laser,Ion and Electron Beams(Ministry of Education),School of Physics,Dalian University of Technology,Dalian 116024,China

Keywords: delta distribution,electronegative plasma,revised spring oscillator,dispersing force

1. Introduction

Low pressure radio frequency inductively coupled electronegative plasma is an important source for applications of etch and deposition in industry. The electronegative molecular gases, such as O2, Cl2, CF4, C4F8, and SF6, etc., are buffered with inertia gases to generate electronegative plasma via gaseous discharge. Regarding its importance,many efforts are made to recognize this type of source,for instance,global model[1]and probe diagnostic[2]of Ar/O2plasma, and fluid simulation of Ar/Cl2plasma.[3]Some other works are focused on the electron dynamics in Ar/CF4plasma,[4]negative ions behavior in C4F8plasma,[5]the fragmentation scheme of it,[6]and the F atoms kinetics in Ar/SF6plasma.[7]

In recent years, numeric technique is widely used in the low-temperature plasma, since the physics in the plasma dynamics is complicated and multiple-disciplinary crossed,which cannot always be predicted by simplified analytic solutions. Spatially, after the inductive electronegative plasma approaches to steady-state,each of charged species in plasma forms their own specific profile, given by the self-consistent simulation. It sounds a little strange that the interesting profiles simulated in the inductive discharges (they are believed to contain the most essential key chemical and physics processes of plasma transport) are rarely noticed. Perhaps, most of the present researchers are mainly focused on the plasma application fields, while not interested in the fundamentals(too basic and boring to them, we guess). Usually, the electrons density and temperature profiles of inductive electronegative plasmas[3,6]are analyzed as in the electropositive plasmas,which are experimentally characterized by the Langmuir probes.[8]However, the multiple ions themselves are important to understand the electronegative plasma, since they are not represented by the electrons and hold their own dynamics as in the ion–ion plasma. In the previous works,[4,5]we occasionally exhibited the self-coagulation behavior of some anion densities,like F−and C4F−8,using the fluid-particle hybrid model;however,this localized type of density distribution needs the support of theory and experiment, since the former interprets the behavior by presenting scientific guesses and the latter validates them. We believe the electronegative plasma components,i.e.,the electrons,ions,neutrals,and the photons(if considered),should be considered simultaneously,for they self-consistently consist of plasma dynamics.

Some analytic works are found in the past years(around 2000), which constructed relatively smooth profiles of electronegative plasmas,[9,12]e.g., parabolic and elliptic profiles,etc.It is shown that the positive ion density profile is parabolic and the electron density is flat at relatively high electronegativity,when the Boltzmann equilibrium of anions is suitable and the positive ions loss via recombination is negligible.Upon increasing the electronegativity,ion density profile evolves into the elliptic type when the ion bulk loss is not negligible and the Boltzmann anion is not applicable. Further increasing the electronegativity, flat-topped profile is observed since the transport of bulk plasma is blocked by the balance of chemical source terms. These old analytic theories are very useful for explaining the simulated electronegative plasma profiles, but are not emphasized at present.

By comparison,we find that less analytic theories are reported for explaining the spatial characteristics of electronegative plasmas at low electronegativities, especially in highdensity plasma sources, like the inductively coupled plasma herein. A little bit of existing works assume the Boltzmann balance of anion. However,in Ref.[13],we found that the anions are not satisfied with the Boltzmann balance at small generating source in an Ar/O2inductively coupled plasma.So,instead of the stratified parabolic profile given at the Boltzmann balance predicted by the analytic method, a simulated novel delta type of negative ions(O−)density is presented via fluid model, as shown in Fig. 1(a). Because the discharge is excited at low electronegativity, the macroscope characteristics of electropositive discharge at ambi-polar diffusion between the electrons and ions is kept. The delta anion density just microscopically tunes the plasma. To be specific,the positive ions (mainly Ar+) profile shown in Fig. 1(b) deviates from the sine function in the axial direction and from the Bessel function along the radial direction. The electron density in Fig. 1(c) just deviates from the Bessel profile in the radial direction. The radial Bessel profile and axial trigonometric profile shown in Figs.2(b)and 2(c)are predicted by the analytic theory of electropositive plasma. Besides, the delta anion causes new phenomena,i.e.,freezing and rebooting of the plasma transport, which has not been observed in the present low temperature plasma.The simulated O−,Ar+,and electron density profiles bend toward the coil slightly, at the influence of heating source of coil electromagnetic field. The selected pressure is 30 mTorr(1 Torr=1.33322×102Pa),a little high.So, the potential of ambi-polar diffusion is adjusted by electron temperature, which is higher at the coil. As the simulation exhibited, at decreasing the pressure, the bending trend is disappeared, when the transport is faster. Benefited from the self-simulation,the temporal behavior of plasma species is investigated in Ref.[13],and quasi-Helmholtz equation composed of anion diffusion and its negative chemical source is deduced,which explains well the forming mechanism of delta function. The delta profile reveals self-coagulation behavior of the plasma inside, possibly triggering new interests of this community in future.

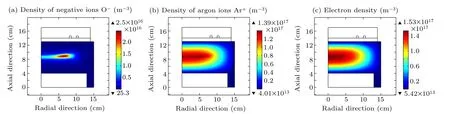
Fig.1. Simulated oxygen negative ions density(a), argon ions density(b), and electron density(c), by means of a fluid model in Ref.[13]. The discharge conditions are 300 W,30 mTorr and 9:1 Ar versus O2 gases ratio. What demonstrated in this plot is that negative ions O−density is a delta type distribution,and both the positive ions and electrons density profile deviate from the analytic solutions,i.e.,trigonometric and the Bessel functions.

Fig.2. Simulated electrons density profile(a)of pure argon plasma by means of a fluid model. The discharge conditions are 300 W and 30 mTorr. (b)Radial distributions of normalized electrons density of argon plasma(black squares)and the zero-order Bessel function(red circles),j0(2.405r/R)(R=15.0 cm),and(c)axial distributions of normalized electrons density of argon plasma(black squares)and the sine function(red circles),sin[(z−4.0)π/l](l=9.0 cm).It is seen that the simulated electrons density profile of electropositive plasma matches the analytic solutions well in both radial and axial directions.

In the present work, the delta profile of anion and selfcoagulation behavior caused are further investigated, and more behind mechanisms are revealed. The one-dimensional(1D) behavior of the quasi-Helmholtz equation established in Ref. [13] is stressed. It is an ordinary differential equation in the high-mathematic knowledge and the delta solution is successfully constructed at set of limits. Stripping the diffusion and chemistry meanings of parameters in the 1D quasi-Helmholtz equation and resupplying them with mass and force, it represents the second Newton’s law. The force derived from the special chemistry is proportional to the displacement. This is a positive feedback system and it exhibits the physics that forms delta displacement. Embedding this replacement into the continuity equation of electropositive plasma that is composed of ambi-polar diffusion and positive source,we found that it essentially represents spring oscillator equation. Accordingly,the Helmholtz equation of electronegative plasma is a revised oscillator equation,since it is driven at a “dispersing” force that keeps driving object away from the reference. This is different with the restoring force of the normal oscillator.

After the above findings extended from the simulated delta that are exhibited in the 1D space, we return to the full-dimensional fluid dynamics. How can a diffusion cause mass assembling, i.e., forming delta density? Which usually smooths up the particle density! We call this “diffusion confusion”. Based on dimensional analysis, it is found that the special negative source that contains the particle density plays the role as inward drift of anions. So,this is a combination of diffusion and drift. The physics of drift is given by the chemistry of source. One example of multiple disciplines crossed!

The basic structure of this article is mathematic formula and a flowchart of the equations is given in Fig. 3 to exhibit their connection. Studies about the delta enrich the knowledge of not only the low temperature plasma physics,but also college physics,e.g.,classic mechanics and aerospace.

Fig.3. Flowchart of the used equations in Section 2.

2. Results and discussion

2.1. Electropositive plasma transport equation

At the approximation of ambi-polar diffusion,[14]the steady state mass transport equation(i.e.,continuity equation)of electropositive plasma is expressed as

Here, Dais the ambi-polar diffusion coefficient. n represents the electrons and ions densities,and νionis the ionization frequency. Further,equation(1)can be written as

The physical properties of Eq. (2) are stripped and the mathematic characteristic is kept. Then, equation (2) is modified as

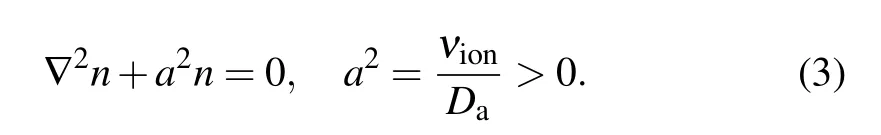
Here,a is real number.

Next,the analysis is focused on arbitrary one-dimensional(1D)space, since we believe that the 1D solution can be representative of any multiple dimensional space behavior. Besides,it is conventional to analyze the physics occurred in single space. The 1D equation is written as

Equation (4) is a linear second-order ordinary differential equation. The general solution of this differential equation is

The above analysis shows that the electropositive plasma transport equation, at the selected definite solution condition,gives rise to sine density profile, which is in general accord with many fluid model predictions.[13–15]

2.2. Spring oscillator dynamic equation

First,the spring oscillator dynamic equation during classic mechanics is reviewed.As we know,the oscillator equation is constructed on the basis of Newton’s law, under the restoring force,i.e.,

Here, A and ϕ are undetermined coefficients (oscillating amplitude and initial phase), and can be given by the initial displacement and velocity of the oscillator,x0,v0. As comparing Eq.(8)with Eq.(4), it is found that the transport equation of electropositive plasma and spring oscillator dynamic equation have the same mathematic characteristic. Up to now,it is understood why the density profile of electropositive plasma is a trigonometric function.

2.3. Decomposed transport equation of electronegative plasma

The decomposed transport equation of electronegative plasma is devised for the negatively charged species. It consists of diffusion flux and the negative source term, i.e., recombination loss of negative ions. As the simulation shows,at the beginning, the drift accumulates anions into the potential bottom at small anions reaction rate,giving rise to high anions density and hence a large negative source term. In the potential bottom, the drift role is weak and the pure free diffusion,together with the negative source term,consists of the decomposed transport equation of anions,i.e.,a new type Helmholtz equation.Note that during these two processes,the Boltzmann relation is not satisfied,as the anions flux is dominated by drift at beginning and then by diffusion afterwards. The Helmholtz equation is expressed as

Here, n−is the negative ions density, D−is the diffusion coefficient of negative ions, and νrecis the recombination frequency of negative ions with major positive ions. Similarly,the transport equation of negative ions is modified as

Here, b is a real number. At the azimuthal symmetry and homogeneous boundary conditions, it has been proved in Ref. [13] that the solution of Eq. (11), i.e., the second-order partial differential equation,is a delta distribution,in the twodimensional axial and radial space. In the present work,it can be further proven that this transport equation has similar delta solution in arbitrary 1D space. Therefore, the 1D version of Eq.(11)is put forward to the following form

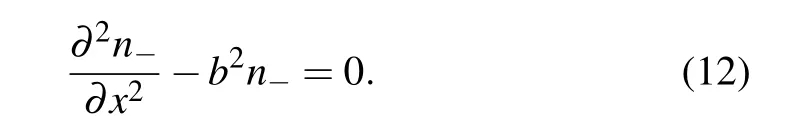
Again,this is a second-order linear ordinary differential equation. Its general solution is

At this limit, the zero solution of Eq. (13) is not really zero. For instance, when x ＞0, the constructed double limit tends to be infinite

Similarly, when x ＜0, the following double limit tends to be infinite,as well.

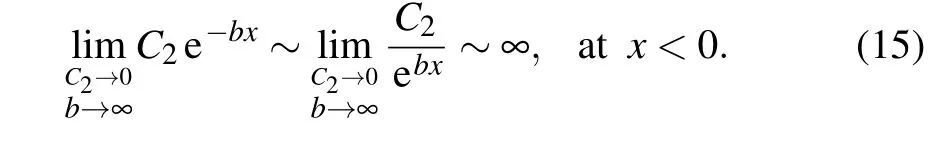
Here, C1, C2are both positive infinitesimals. So, the constructed solution is

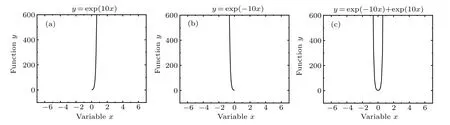
Fig.4.Schematic plot of Eq.(16)that predicts the downward quasi-delta.The discussed mathematic transformation beneath that gives rise to normal upward quasi-delta based on Eq.(16).

For constructing real delta, effective transformations are made to the above solution during the small segment around origin,i.e.,

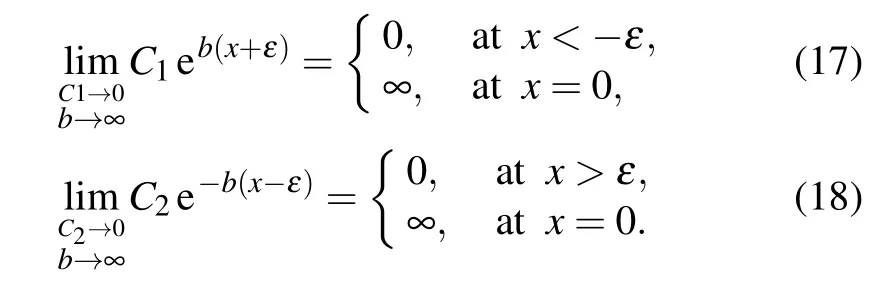
At the limit of ε →0,the solution in this segment turns into a conventional delta function,i.e.,

Clearly, this is a delta-type solution after the equivalent transformation. This mathematic transformation is analogous to the Fourier and Laplace transformations learned in the Method of Mathematical Physics. Or more precisely,it is like the improper integral that contains singularity of integrand along the integrating path. Meanwhile,this solution advances the knowledge of Generalized Functions, i.e., it provides one more method to construct the delta function,by means of differential equation.

The above delta is located at the position of x=0.In fact,the location can be shifted within the studied spatial range.From the general solution, Eq. (13), by making a change to the general solution,i.e.,

where x0is any position within the border. Applying a similar procedure to Eq. (20), we obtain a new delta solution as follow:

Apparently,this conclusion is in accord with Ref.[13]: when a delta is independent of the spatial coordinates, in the radial and axial two-dimensional space.It is reasonable,since within the studied spatial range,wherever the b value is large enough,a delta is formed. The key point is the b value. In Ref. [13],the location of O−delta is determined by the fact that obvious negative source is formed at a certain spatial location, since the order of recombination frequency, ～104, is rather larger than the diffusion coefficient,～10−1.

2.4. Revised“spring oscillator”equation

It is easy to analyze the physics behavior implied in the 1D negative ions equation. To exhibit the relevant physics,the ordinary spring oscillator equation,Eq.(7),need to be revised.A dispersing force, instead of the restoring force, is applied,i.e.,

Why the original restoring force, f =−kx,after changing the math symbol, plays roles as dispersing force, i.e., F = kx?First, the definition of restoring force and the related final trigonometric function solution of the oscillator are reviewed.The direction of the restoring force is contradicted to the displacement. This means that once the object deviates from the selected reference location,the restoring force pulls it back to the reference. Together with the object inertia (described by the left side of Eq.(7)),the object oscillates around the reference. This composes the trigonometric function solution.

Different from the resilience,the dispersing force causes the displacement. It means that when the object deviates from the reference, the dispersing force will push it far away from the reference. Under the dispersing force, as well as the displacement is occurred,the object will keep moving away from the reference and can never be turning back to the reference.From this explanation,the dispersing force,can also be called as diverging or driving force. At this type of forces, the amplitude of object displacement,once happened,will tend to be infinite. Accordingly,the test solution of revised spring oscillator equation at dispersing force can be constructed,

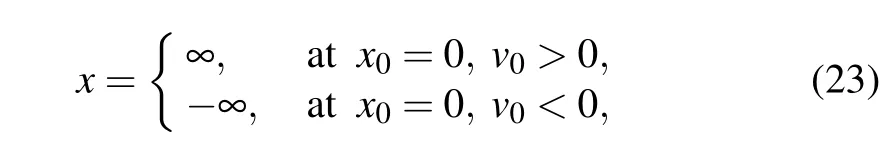
where x0and v0are the initial displacement and velocity of the object, respectively. Logically, one prerequisite is needed for the reasonability of Eq.(23), i.e., the effective stiffness coefficient k, ought to be as large as possible and meanwhile the object mass m, ought to be as small as possible. Mathematically, this is a parametric equation, the solution relies on the parameter values.

The above analysis of the revised oscillator equation is one constructed solution. Within the time domain,the analytic solution of Eq.(22),at fixed initial conditions,x0=0,v0,is existed. Equations(24)and(25)present the general and definite solutions,respectively

where,ω is the transformed angular frequency.When increasing t,for large angular frequency value,the negative exponential term tends to zero. The analytic and constructed solutions,i.e.,Eqs.(25)and(23),match each other.

It is noticed that the main mathematic feature,i.e.,infinity is kept by the solutions of decomposed electronegative plasma and revised oscillator equations,but meanwhile certain differences are existed, e.g., delta and infinity, and their locations.Mathematically, this is acceptable since the controlling equations are the same while the definite conditions are different.With respect to physics, it is understandable since the transport equation considered is for a steady state case while the revised oscillator is an unsteady state case. The delta solution of the revised oscillator may relate to the fact that scattered micro-species at the dispersing forces directing to a reference location,converge into one macro-object,like the collider experiment.

In the end, the potential physics that cause dispersing forces are examined, e.g., universal gravitation and electric field force of positive or negative point charge. As seen,these conventional forces of classic mechanics all hold the feature of dispersing or/and diverging forces. Of more significance is that it is possible the revised oscillator equation with dispersing force,initiated by the negative ions transport equation,plays roles in forming atoms and celestial bodies of universe,as predicted by Eq.(26)below:

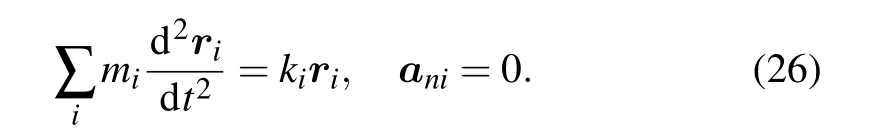
Here,aniis the normal acceleration,with the initial velocities,v0i,all directing to the fixed reference location. In a word,this little differential equation,Eq.(22),probably is meaningful to the curriculums of atomic physics and astronomy.

In the end of this section,we discuss the integral property of this constructed delta function given by the above differential equations by using Eq. (26). Since all of the mass flow to the reference point at the dispersing force,so all of mass finally concentrated to the point as well,in accord to the integral property of the delta function.

2.5. Physics of negative ions delta and the “diffusion confusion”

The above sections give rise to a delta distribution for the negative ions transport equation,mostly based on the math and the Neuton’s law. In this section,the physics of negative ions delta in the field of fluid dynamics is explored. Besides, the proposed “diffusion confusion” that the diffusion increases,instead of attenuates, the density gradient, is clarified. One unsteady state transport equation of negative ions, based on Eq. (10), is constructed, which is helpful for exploring the physics of delta,as shown below:

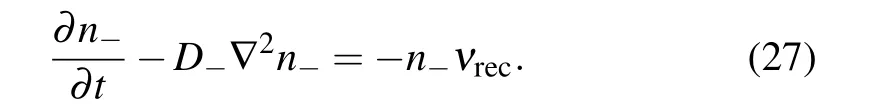
Superficially, this is one transport equation, mainly made of diffusion and source (i.e., chemical reactions). Nevertheless,the source term,because it contains the species density,actually plays roles as drift of the electric field, by means of the dimension analysis of source and drift terms.

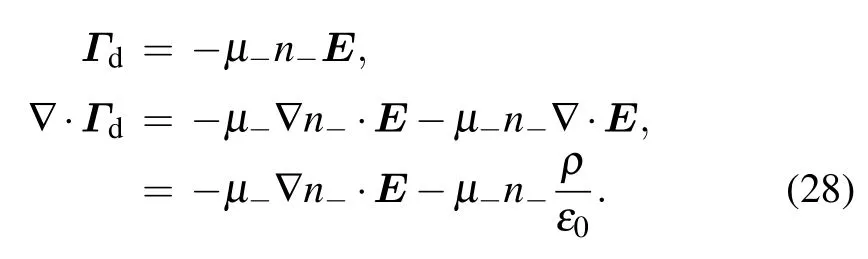
In Eq. (28), the drift flux, Γd, and its divergence are shown.Here, E is the electrostatic field, and ρ is the net charge density. In deducing the divergence of drift flux, the Poisson’s equation is utilized. The dimensional analysis is executed onto the term, −µ−n−(ρ/ε0), shown below. The term,−µ−∇n−·E, is not selected for the dimension analysis, because it has the density gradient,which is not appeared in the source term. Evidently,the dimension of the chosen drift flux divergence component is the same with source.

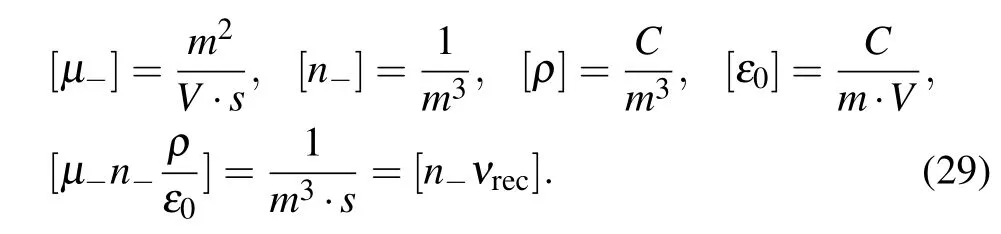
Since the expression of the chosen drift flux divergence term is similar to the source term,and the dimensions of them are the same, it is hence believed that the source term can play roles as drifting electric field.

One test equation is constructed for conveniently analyzing the direction of effective electric field,given by the source term,as shown below:

In Eq. (30), the diffusion flux is excluded and one hypothesized drift flux is embedded. Replacing the drift flux divergence of Eq.(30)with the term,−µ−n−(ρ/ε0),it turns into

Herein,it was the hypothesized drift flux driven by the ambipolar potential,when observing Eq.(31),it seems that the effective source drift flux directs reversely. Was this true, the source drift diverges negative ions, and the delta distribution can never be formed. The truth is that the hypothesized drift flux (conventional) considers the negatively charging property of anions,while the transformed source drift flux(novel)does not. Regarding this fact,the more reasonable formula of Eq.(31)ought to be

After this revision, it is clear that the source drift, represented actually by the term −n−νrec, directs to the hypothesized ambi-polar electric field. Hence, the effective field of the source term,once formed,attracts negative ions,ab intra.

The negative ions transport equation is rewritten here with a tiny change,

At the special source term, the transport equation is not essentially pure diffusion issue and thereby cannot be simply described by the general Fourier’s law. Actually, the transport equation of positive plasma, i.e., Eq. (1), is not equal to the Fourier’s law, either, as the essential vibration solution is gotten (refer to Eqs. (7)–(9), which is usually unable to be predicted by Fourier’ law. In addition, although the general source term, when including not the density of species being studied,holds the same dimension,it cannot be transformed as drift term, as the drift flux divergence explicitly contains the studied species density; see Eq.(28). If the general source is used (e.g., many instances occurred in general fluid mechanics), still, it is essentially issue determined by Fourier’s law.Meanwhile,the math property of equation is changed,and the quasi-Helmholtz type,implied in Eqs.(2)and(11),is lost. In another word, this peculiarity is presently suited to the fluid dynamic investigations of low temperature plasma, which is self-generated by gaseous discharges via seed electrons.

3. Conclusion

In the work, reformed“spring oscillator”dynamic equation with dispersing instead of restoring force is suggested for mathematically interpreting the delta profile of electronegative plasma.The physics that determines the delta is also searched,i.e., the species loss source term that carries the considered species density plays roles as drift flux. Besides, the importance of one parameter in generating delta solution, i.e., the ratio of species loss frequency versus diffusion coefficient of species,is emphasized,for it represents the acceleration of object that directs and is proportional to the displacement. All these new findings supply more facets for people understanding better the formation of delta distribution(initially reported in one companied work[13]),within the framework of both low temperature plasma and general physics fields. Moreover,the revised oscillator equation is of possible interest to the disciplines of atomic physics and astronomy, as it describes the process of mass assembling at proper conditions,creating objects like atoms, molecules, and the astral bodies in the Universe. The supporting evidence might be that the simulated anion delta looks like a comet, as shown in Fig. 1(a) of this article.

This research is hope to be beneficial for researchers to understand the electronegative plasma sources especially at low electronegativities, and meanwhile advances the analytic theory of low temperature plasma. Still, the related mathematic knowledge is updated,and a new mean to construct the delta function is provided by means of differential equation,which develops the scope of Generalized Functions. In addition,the new methodology is deduced from the above studies,i.e., to extract the physics and math knowledge from the virtual simulations that predict potential and novel phenomena.Namely, the numeric simulation and analytic science are developed collaboratively,to interpret the real world,besides for the experimental diagnostics.

Acknowledgements

The DUT19LK59 foundation is acknowledged for the financial support. The time when being assistant teacher for the course of College Physics of Prof. Shu-Feng Li is also appreciated,for it helps the author,Shu-Xia Zhao,reviewing the oscillator model knowledge.