Controllable four-wave mixing response in a dual-cavity hybrid optomechanical system*

Lei Shang(尚蕾), Bin Chen(陈彬),2,†, Li-Li Xing(邢丽丽), Jian-Bin Chen(陈建宾),Hai-Bin Xue(薛海斌), and Kang-Xian Guo(郭康贤)

1Department of Physics,College of Physics and Optoelectronics,Taiyuan University of Technology,Taiyuan 030024,China

2Key Laboratory of Advanced Transducers and Intelligent Control System,Ministry of Education and Shanxi Province,Taiyuan 030024,China

3Department of Physics,School of Physics and Material Science,Guangzhou University,Guangzhou 510006,China

Keywords: four-wave mixing,dual-cavity optomechanical system,atomic ensemble

1. Introduction

In the past few decades, the nonlinear optical effects[1]caused by the interaction between light and matter have been a striking research topic and optomechanical systems,[2–10]as a good platform for studying nonlinear optical effects, have received a great deal of attention. The most typical optomechanical system is composed of an optical cavity with a mechanical resonator. Recently, researchers have extended single-cavity optomechanical systems to hybrid cavity optomechanical systems[11–18]by coupling more optical or mechanical modes,such as an atomic ensemble,a quantum well,a Kerr medium or other media with optomechanical cavities. More optical effects, such as electromagnetically induced transparency,[19–26]optical bistability,[27–31]slow light effects[32–37]and so on, have been extensively explored in these hybrid systems.

Currently,the four-wave mixing(FWM)effect,[37–49]one of the classic nonlinear effects, is widely studied in optomechanical systems. Jiang et al.[37]investigated how to control the FWM process in a two-mode cavity optomechanical system. In a three-mode optomechanical system with atom–cavity mirror coupling, Wang and Chen[39]confirmed that the FWM response can be well enhanced. In a composite photonic-molecule optomechanical system,Chen et al.[40]studied the process of normal mode splitting in the FWM spectrum under different parameter and driving conditions. Li et al.[41]realized multimode FWM in an unresolved sideband optomechanical system.

Inspired by the above work, we explore the FWM process in a hybrid dual-cavity optomechanical system with cavity A containing an ensemble of two-level atoms and cavity B coupling a mechanical oscillator. We mainly pay attention to the FWM effect in cavity B and investigate the dependence of the FWM on system parameters such as pump power,coupling strength, detuning, etc. Here, we propose a scheme in which this optomechanical system can serve as an optical mass sensor and an all-optical switch based on measurement of the FWM spectrum. These schemes are important for potential applications of this hybrid system in quantum information processing or highly sensitive detection. The structure of this paper is as follows: In Section 2,the theoretical model and theoretical calculation of the equation are introduced. Section 3 focuses on the analysis and discussion of the results. Section 4 presents a summary.

2. Theoretical model

As depicted schematically in Fig. 1, the dual-cavity hybrid optomechanical system considered in this paper is composed of optical cavity A containing an atomic ensemble and cavity B interacting with a mechanical oscillator.

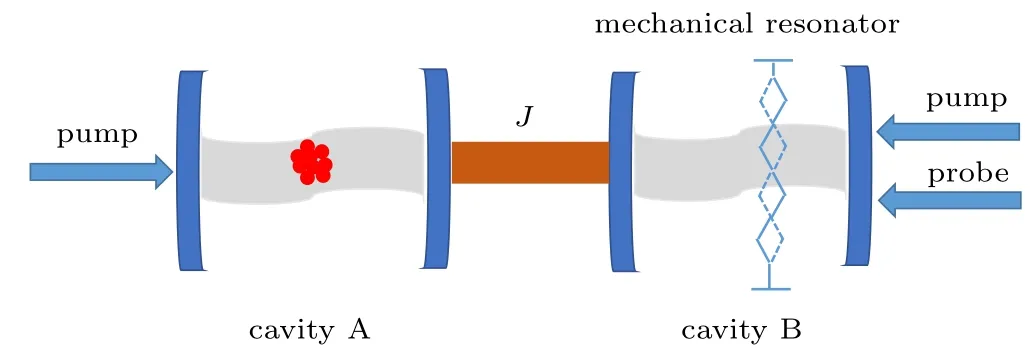
Fig. 1. Schematic of a dual-cavity hybrid optomechanical system, where two cavities have identical lengths L and mode frequencies ωc.

These two cavities are coupled with each other via an evanescent field and the coupling strength is denoted as J. In addition, cavity A is driven by a strong pump light with frequency ωp1and amplitude εp1,while a strong pump light with frequency ωp2and amplitude εp2as well as a weak probe light with frequency ωprand amplitude εprare applied to cavity B.For simplicity, the frequency ωp1is chosen to be the same as ωp2,and cavities A and B are assumed to have the same mode frequency ωc. In a frame rotating at ωp2, the Hamiltonian of this system can be written as follows:

In Eq. (3), we phenomenologically add the cavity decay rate κ, the atomic coherence decay rate γaand the damping rate of the mechanical oscillator γm,and ignore quantum and thermal noise terms. To solve the above equations, we make the following ansatz:

where x0, p0, a0, b0, A0are, respectively, the steady-state solutions of x, p,a,b,A. By substituting Eq.(4)into Eq.(3)and solving these equations,we can get

with

where the first two terms in Eq.(7),respectively,describe the output fields at frequencies ωp2and ωprwhile the last term depicts an output field of FWM.

A relative output field intensity of FWM from cavity B can be defined in terms of the probe field as follows:

3. Results and discussion

In order to reveal the FWM process more concisely, we choose the realistic experimental parameters of the dual-cavity hybrid system[37,39]as λ =1064 nm,l=1.5 mm,m=10 ng,ωm=2π×10 MHz, κ =2π×1 MHz, γm=2π×100 Hz,γa=2π×5 MHz,∆a=−1.0ωm,∆c=1.0ωm.

Figure 2 shows the FWM intensity IFWMas a function of the probe-pump detuning δ/ωmfor two different pump schemes. As is shown in Fig. 2(a), when the left pump laser is off (Pp1=0) but the right one is on, two strong peaks appear at δ ～±ωmin the FWM spectrum, which exactly correspond to the vibrational frequency of the mechanical oscillator. Most interestingly,for the opposite pump schemes,i.e.,the left pump laser on and the right one off(Pp2=0),the two FWM peaks at δ ～±ωmbecome much narrower as shown in Fig. 2(b), while their intensity only suffers a small reduction. These important results demonstrate that this dual-cavity hybrid optomechanical system can be used as a sensitive quantum sensor, for example as a mass sensor,[52]when it is only driven by a left pump laser. It is well known that,for a quantum sensor,the spectrum width is an important factor affecting its sensitivity.[52]The narrower the spectral width is,the more high resolution of the sensor will be. Taking the mass sensor proposed in the reference[52]as an example,its sensitivity and resolution could be significantly enhanced by introducing a plasma into the system as the probe spectrum width was modulated effectively.

Fig.2. The FWM intensity IFWM as a function of the probe-pump detuning δ/ωm for the case:(a)Pp1=0 and Pp2=10 mW,(b)Pp1=10 mW and Pp2=0. The other parameters are taken as λ =1064 nm,l=1.5 mm,m=10 ng,ωm=2π×10 MHz,κ=2π×1 MHz,γm=2π×100 Hz,γa=2π×5 MHz,∆a=−1.0ωm,∆c=1.0ωm,G=2π×5 MHz,J=2π×1 MHz.

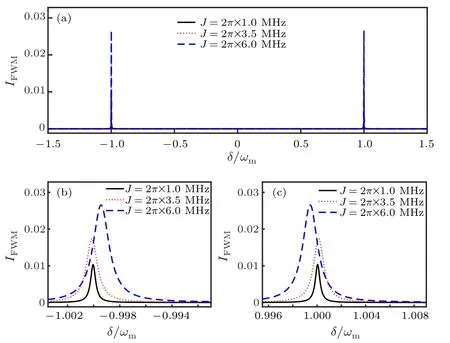
Fig.3. (a)The FWM intensity IFWM as a function of the probe-pump detuning δ/ωm for the case that Pp1 =10 mW and Pp2 =0 with different cavity coupling strength J=2π×1.0,2π×3.5,and 2π×6.0 MHz. (b)and(c)are,respectively, the enlarged images of the left and right peaks in (a). Other parameters used are the same as in Fig.2.

In the following discussions,we mainly consider the case that only the left pump laser is opened. Figures 3 and 4, respectively, present the dependence of the FWM signal on the cavity–cavity coupling strength J and on the atom–cavity coupling strength G for this pump scheme. In Fig.3(a),the FWM intensity IFWMis plotted as a function of the probe-pump detuning δ/ωmfor different coupling strength J. Figures 3(b)and 3(c), respectively, show the enlarged images of the left FWM peak and the right one in Fig. 3(a). It is obvious that with the increase of the coupling strength J both the left and the right peak in the FWM spectrum rise sharply, i.e., the FMW signal is significantly enhanced, and at the same time both peaks suffer a small shift. This phenomenon can be explained as follows. With the increase of the coupling strength between cavity A and B, it will be more and more easy for the pump photons to enter into cavity B,and thus the number of pump photons entering cavity B per second will increase,which will promote the process of FWM generated in cavity B as a result. Moreover,it is well known that increasing the photon number in the cavity can effectively shift the mechanical frequency,so as result the FWM peaks are shifted as well.

Fig.4. (a)The FWM intensity IFWM as a function of the frequency detuning δ/ωm for different atom-cavity coupling strength G=2π×5.0, 2π×7.0,and 2π×9.0 MHz. (b)and(c)are, respectively, the enlarged images of the left and right peaks in(a). Here,J=2π×6.0 MHz,Pp1=10 mW,Pp2=0,and other parameters used are the same as in Fig.2.

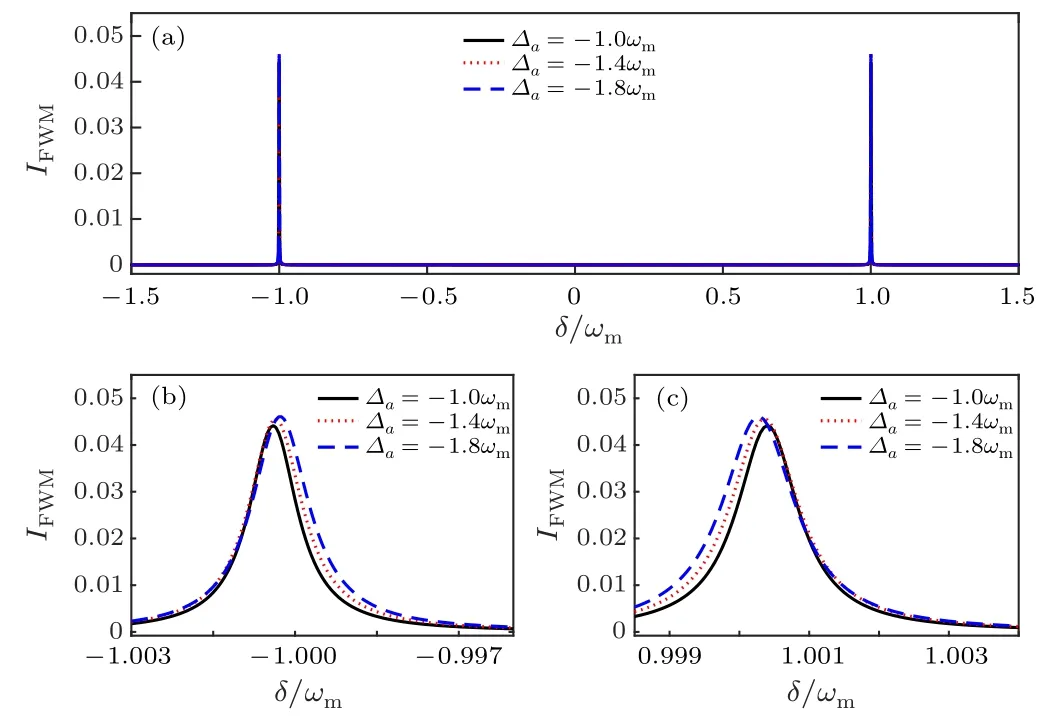
Fig. 5. The FWM intensity IFWM as a function of the frequency detuning δ/ωm for atom-pump detuning ∆a ＜0. (b)and(c)are,respectively,the enlarged images of the left and right peaks in (a). Here J =2π×6.0 MHz,G=2π×9.0 MHz,Pp1=10 mW,Pp2=0,and other parameters used are the same as in Fig.2.

Figure 4 depicts the FWM intensity IFWMas a function of the probe-pump detuning δ/ωmfor different atom–cavity coupling strength G. This figure clearly shows that the FWM signal generated in cavity B can be significantly strengthened via increasing the atom–cavity coupling strength G in cavity A. In addition, it is obvious that the FWM peaks also have some shift. The phenomena can be attributed to the indirect modulation of cavity A to cavity B.As the atoms interact with the cavity,the distribution of the field intensity in cavity A will be adjusted by the atom–cavity coupling strength. Indirectly,the field intensity of cavity B can also be affected, and as a result the FWM signal generated in cavity B is modulated effectively by the atom–cavity coupling strength.

Fig.6. The FWM intensity IFWM as a function of the frequency detuning δ/ωm for atom-pump detuning ∆a ＞0. Other parameters used are the same as in Fig.5.

Figures 5 and 6 illustrate the FWM intensity IFWMas a function of the probe-pump detuning δ/ωmfor two opposite detuning case, i.e., ∆a＜0 and ∆a＞0. Figure 5 shows that the FWM signal is not sensitive to the atom-pump detuning∆afor the blue detuning case, i.e., ∆a＜0. However, in the opposite case,it is a completely different situation. As shown in Fig.6,for the red detuning case,i.e.,∆a＞0,the FWM intensity is enhanced significantly with the increase of the atompump detuning ∆a. Most interestingly,at the resonant region,i.e., δ ～0, a prominent peak appears in the FWM spectrum.These phenomena can be easily understood as follows. When the beat frequency δ between the probe and the pump light is approximately equal to the frequency of the mechanical resonator,i.e.,δ ～±ωm,the mechanical mode starts to oscillate coherently,which will induce the generation of FWM.[21]As a result,two strong FWM peaks appear at δ ～ωmand −ωm,respectively,as shown in Figs.5 and 6.However,at δ ～0,it is the resonance between the pump light and the probe light that induces the generation of the FWM.In addition,strong pump light is also needed.It is well known that for ∆a＜0,the pump light is strongly absorbed by the atoms,[55]so the photon numbers in cavity B is not enough to induce the FWM generation.For ∆a＞0,the absorption of the atoms is reduced,[55]so more pump photons can enter into cavity B,and as a result the FWM process at δ ～0 is opened for this case as shown in Fig.6.

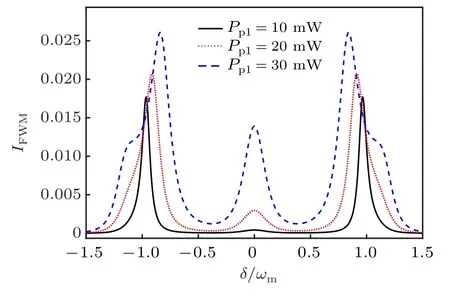
Fig.7. The FWM intensity IFWM as a function of the frequency detuning δ/ωm for different pump power Pp1 =10, 20, and 30 mW. Here,∆a=1.4ωm,J=2π×6.0 MHz,G=2π×9.0 MHz,Pp2=0,and other parameters used are the same as in Fig.2.

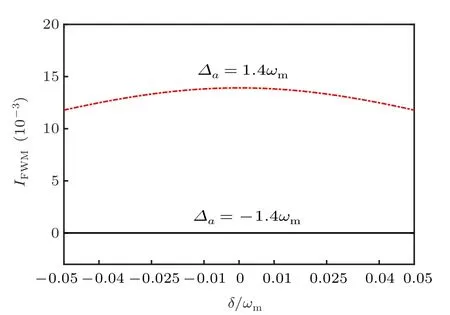
Fig.8. The FWM intensity IFWM versus the frequency detuning δ/ωm for different atom-pump detuning ∆a. Here, Pp1 =30 mW, Pp2 =0,J=2π×6.0 MHz,G=2π×9.0 MHz,and other parameters used are the same as in Fig.2.

In Fig. 7, the influence of the pump power on the FWM intensity IFWMfor the red detuning case is considered,and the FWM intensity IFWMis plotted as a function of the frequency detuning δ/ωmfor different pump power with ∆a=1.4ωm.From this figure, it can be clearly observed that as the pump power rises the FWM intensity is largely increased. Importantly,it is obvious that the resonant peak of the FWM intensity at δ ～0 is highly sensitive to the pump power, so it is largely improved by the increasing pump power.

The results of Figs. 5–7 show us that this hybrid twocavity optomechanical system can serve as an all-optical switch.[53,54]To illustrate this idea clearly, Fig. 8 is plotted,which presents the FWM intensity IFWMversus the frequency detuning δ/ωmfor two different atom-pump detunings.When∆a=−1.4ωm,as is shown in Fig.8,there is no FWM signal generated in this hybrid system at the resonant region (i.e.,δ ～0). However, when the atom-pump detuning ∆ais tuned to 1.4ωm,a prominent FWM signal appears at δ ～0. Therefore,this system can act as an all optical switch,and the FWM signal at the resonant region can be easily opened or closed by tuning the atom-pump detuning to be positive or negative.

4. Conclusion

In conclusion, we have theoretically analyzed the FWM effect in a dual-cavity hybrid optomechanical system. First,we propose a mass sensor plan based on this hybrid system for its narrow FWM spectrum,and the numerical results show that the sensitivity and accuracy of the sensor can be improved by adjusting the cavity–cavity or atom–cavity coupling strength.Secondly,we find that the FWM effect at the resonant region can be modulated by controlling the atom-pump detuning to be positive or negative. For this reason, we put forward that the hybrid dual-cavity optomechanical system can be used as an all-optical switch. Finally,we hope that the proposed scheme can be proved experimentally in the near future.