Application of non-Hermitian Hamiltonian model in open quantum optical systems*

Hong Wang(王虹), Yue Qin(秦悦), Jingxu Ma(马晶旭), Heng Shen(申恒),3,Ying Hu(胡颖), and Xiaojun Jia(贾晓军),3,†

1State Key Laboratory of Quantum Optics and Quantum Optics Devices,Institute of Opto-Electronics,Shanxi University,Taiyuan 030006,China

2State Key Laboratory of Quantum Optics and Quantum Optics Devices,Institute of Laser Spectroscopy,Shanxi University,Taiyuan 030006,China

3Collaborative Innovation Center of Extreme Optics,Shanxi University,Taiyuan 030006,China

Keywords: non-Hermitian Hamiltonian,open quantum system,optical parametric processing

1. Introduction

In standard quantum mechanics, a closed system is described by the Hermitian Hamiltonian and the associated real eigenvalues spectrum. However, there always exist channels between the system and the environment,which are built through the force driving, dissipation, or fluctuation induceddissipation. Such a system is generally called an open quantum system.[1–3]Open systems with dissipation have been a subject of significant interest in physics and can be described by non-Hermitian Hamiltonians in contrast to standard quantum mechanics requiring Hermiticity. Exceptional points(EP),known as non-Hermitian degeneracies or branch points,correspond to special points in parameter space at which both the eigenvalues and the eigenvectors of the non-Hermitian Hamiltonian simultaneously coalesce. A number of intriguing physical effects related to EP have been observed in optical gain-loss systems, such as topological chirality, potentially enhanced sensitivity, and phase transition in the case of PT-symmetry breaking.[4–8]When describing the open system of interaction between a light field and a multi-level system, the decay term is often introduced into the Hamiltonian to reflects spontaneous emission or ionization and the decay of the system population.[3,9–11]In the optical parametric processing,the dissipation caused by the interaction between the environment and the cavity reflects the lifetime of the corresponding eigenstate.[12]Quantum decoherence is also the result of entanglement between the open quantum system and environment.[13–16]

In this article,we apply the non-Hermitian quantum theory in the open optical quantum system,where the dissipation is included in the Hamiltonian. Dissipative phase transition is observed and is attributed to the competition between the coherent interaction and dissipation. Furthermore, quantum correlation in terms of squeezing is analyzed here.

Fig.1.The schematic of the quantum mechanics developing from Hermitian to non-Hermitian.

2. Theoretical simulation of an open quantum system

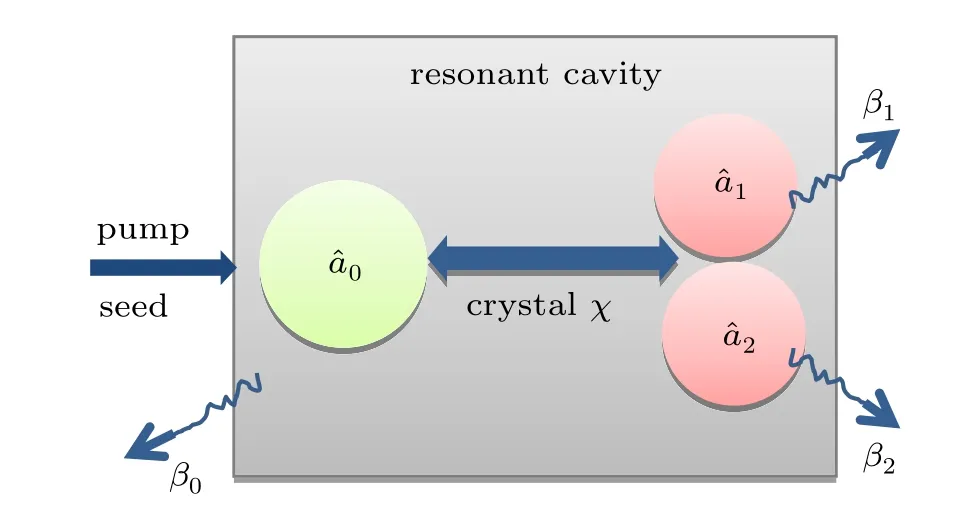
Fig. 2. Schematic of the open quantum optical system considered. One pump photon ˆa0 converts into a pair of lower-energy photons, ˆa1 and ˆa2 subject to both energy conservation and the cavity resonance condition. The corresponding transmission loss rates are βi(i=0,1,2). χ is the nonlinear factor.

The non-Hermitian Hamiltonian of such an open system can be expressed as follows:

Considering the aforementioned Bogoliubov transformation and bosonic commutation relation, the following result can be obtained:

3. Dissipative phase transition and the associated quantum correlations

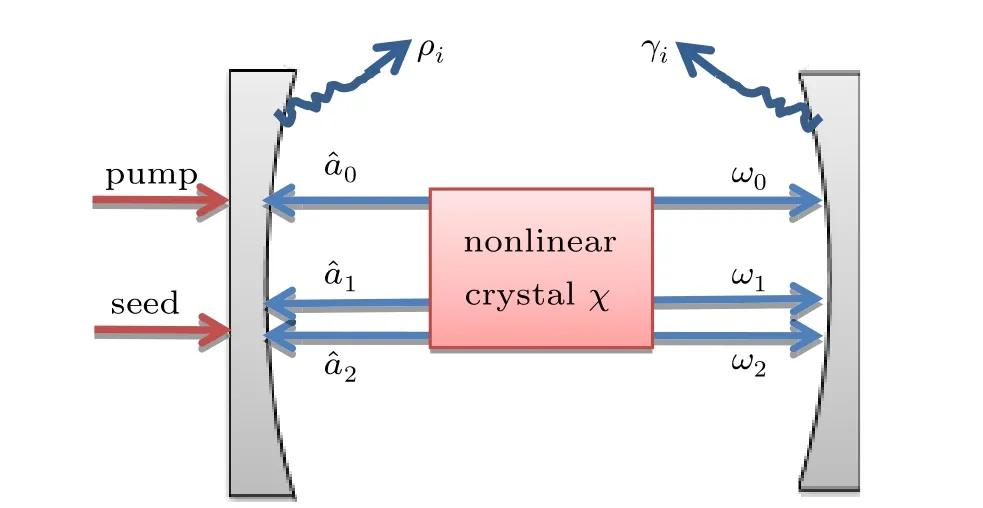
Fig. 3. Schematic of the optical parametric processing. Pump mode with the frequency of ω0,signal modewith the frequency of ω1 and idle mode with the frequency of ω2 are interactive in the cavity. γi and ρi(i=0,1,2)are the transmission loss rates of the output and input mirror to the three modes in the cavity,respectively. χ is the nonlinear coefficient.

Hence,the solutions of steady state are as follows:

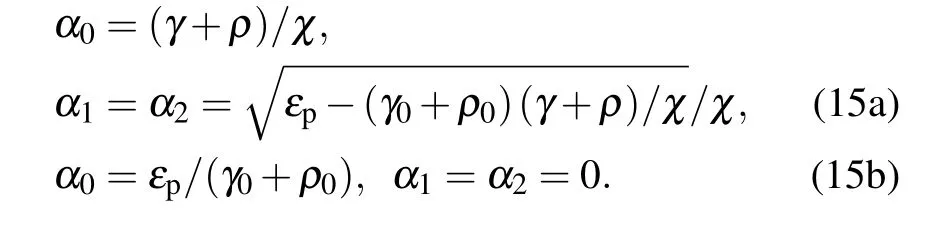
According to Eq.(15),only when εp−(γ0+ρ0)(γ+ρ)/χ ＞0,α1=α2/=0 is true. That is to say,when εp＞εthres(threshold: εthres= (γ0+ρ0)(γ+ρ)/χ), the steadystate solutions above the threshold are Eq. (15a), and the signal mode and idle mode oscillate in the cavity where the coherent interaction is dominant. Otherwise, the steady-state solutions below the threshold are Eq. (15b), and the signal mode and idle mode will be in the vacuum field (α1=α2=0) where the loss is dominant.

As expected, a dissipative phase transition (secondorder phase transition) occurs around the threshold of pump light in such a system. Figure 4(a) shows order parameters αi(i=1,2)as a function of the intensity of the driving pump light εp. We introduce k=χα0/(γ+ρ). If the pump power is below the threshold,k=εp/εthresand 0 ≤k ＜1 are obtained by the solution of steady state. If the pump power is above the threshold,then one gets k=1.

Fig. 4. Dissipative phase transition in the open quantum optical system.(a) Order parameters αi (i=1,2) for γ0+ρ0 =10, γ+ρ =1, χ =5, and εthres=2 as a function of the intensity of the driving pump light εp. (b)The imaginary parts of eigenvalues E0 (brown curve) and E1 (blue curve) as a function of εp/εthres. The red dashed line shows the position of the threshold,the so-called critical point.

The dissipative coefficient γ+ρ here corresponds to β of part 2. According to Eq.(7),the Hamiltonian with the secondorder quantum fluctuation term can be rewritten as

As an example,we look at the eigenvalues E0and E1corresponding to ¯bb=0 and 1, respectively. Figure 4(b) shows the imaginary parts of E0(brown line) and E1(blue line) in the unit of γ+ρ as a function of εp/εthres, respectively. The part of 0 ≤εp/εthres＜1 corresponds to the situation below the threshold,and the part of εp/εthres＞1 corresponds to that above the threshold, indicated by the red dashed line in the figure. Strikingly, there also exists the non-analytical behavior for both curves in the threshold, the critical point. Below the threshold, the higher the pump power is, the faster the eigenstate dissipates. Above the threshold, as the pump power continues to increase,the dissipation will tend to saturation. In terms of the order parameters and the eigenvalues of the non-Hermitian Hamiltonian, it indicates that a dissipative phase transition(second-order phase transition)occurs around the threshold of pump light in such a system.

We proceed to discuss the quantum correlation in terms of squeezing. Figure 5 shows 〈|δ ˆXd1|2〉 and 〈|δ2〉 as a function of εp/εthres, indicated by the green and purple solid curves, respectively, and the black solid line represents SNL.Below the threshold,the noise of the amplitude quadrature operator is raised above the SNL, while the noise of the phase quadrature operator is squeezed below the SNL. And by increasing the intensity of pump light to approach the threshold,the nonclassical optical field with a higher squeezing degree can be achieved. However, above the threshold, with the increase of pump power, the squeezing degree tends to saturation. In terms of the quantum correlation,it similarly indicates that a dissipative phase transition (second-order phase transition)occurs around the threshold of pump light.

Fig.5. The green and purple solid curves represent quantum fluctuation of δ ˆXd1 and δ ˆPd1 as a function of εp/εthres,respectively.The red dashed line shows the position of the threshold,the so-called critical point. The black solid line represents SNL.

In summary, the existence of dissipative term leads to the threshold to be non-zero,which leads to the second-order phase transition of the order parameters, the eigenvalues of non-Hermitian Hamiltonian and the quantum correlation near the threshold. And the larger the dissipation is, the larger the threshold value will be. Then the intensity of pump light is needed to be bigger than the threshold value to eliminate the domination of dissipation and make the signal mode and idle mode oscillate in the cavity. Otherwise, the signal mode and idle mode will be in the vacuum field because their steadystate solution is zero below the threshold. That is to say, the dissipative phase transition is attributed to the competition between the coherent interaction and dissipation.

4. Conclusion and perspective

We report the application of non-Hermitian theory in an open quantum optical system.Due to the competition between coherent nonlinear interaction and the dissipation induced by the system loss, a dissipative phase transition is observed.Moreover, we analyze the quantum correlations in terms of squeezing around the critical point.Our work provides new insight into the quantum simulation of the non-Hermitian quantum system,especially the quantum properties.