基于变分模态分解与图信号指标的配电网高阻接地故障识别算法

肖启明 郭谋发

（福州大学电气工程与自动化学院，福州 350108）

0 引言

在配电网中，线路接触混凝土、草地、砂石等高阻抗导体表面时，易发生高阻接地故障（high impedance fault, HIF），其故障电流幅值低，传统过电流继电器无法检测到[1]。尽管较低的电流幅值不易损坏电力系统的元件，但由于HIF常伴随着电弧的燃烧，因此会危及动物与人类的生命安全，甚至引发火灾造成重大经济损失[2]。相关报告指出，在配电网故障中，大约有5%～20%是HIF[3]，但随着配电网结构日趋复杂[4-5]，实际HIF比例已远高于该数值。

经过大量专家的研究，现有的高阻接地故障识别方法可分为时域法、频域法与时频域法。时域法通常基于电压、电流信号的时域特性。文献[6]将零序电流的功率变化量作为故障的判断依据。文献[7]利用数学形态学技术来提取故障电流的特征。文献[8]利用故障电流连续半周波间的KL（Kullback-Leibler）散度作为HIF检测指标。时域法虽然结构简单，但可能会丢失重要的频域信息，降低方法的有效性。

频域法基于HIF电信号的高低频分量特性。文献[9]将低次谐波的总能量作为HIF判断标准。文献[10]利用低次谐波之间的距离变化来检测HIF。频域法虽然能够利用HIF的频域特征，但由于非线性负载与HIF的频域特征过于相似，因此无法将其区分。

近年来，在时频域研究中涌现了多种HIF检测技术。文献[11]使用局部特征尺度分解（local characteristic scale decomposition, LCD）构造三相电流的时频矩阵，各个频带的标准差作为HIF特征。文献[12]利用经验模态分解（empirical mode decomposition, EMD）得到的本征模态分量（intrinsic mode functions, IMF）作为故障特征，以此训练人工神经网络（artificial neural network, ANN）来区分HIF与非HIF。文献[13]结合变分模态分解（variational mode decomposition, VMD）与时间熵为HIF检测引进了新的故障指标。文献[14]使用小波分解（wavelet decomposition, WT）与软阈值降噪技术作为HIF现场检测手段。VMD相较WT，避免了人为选择母小波的过程；相较EMD，避免可能出现的模态混叠效应；相较LCD，具有更不明显的端点效应。因此选用VMD作为故障特征的提取手段。

当配电网发生HIF与投切事件时，零序电流的本征模态分量图会发生结构变化，图内每条边的权值相应改变，而图信号指标[15]作为图矩阵的特征值函数，能有效区分不同的变化。因此，本文结合VMD与图信号指标，提出一种全新的HIF识别算法。

1 高阻接地故障识别算法

1.1 变分模态分解

VMD是一种能将任意信号f(t)分解为多个模态信号的分解方法。具体步骤如下：

1）假设f(t)由有限个具有稀疏特性的本征模态分量{u1,…,uK}构成，其中心频率分别为{ω1,…,ωK}，将各模态分量的聚集带宽之和的最小值作为优化的目标函数，则有

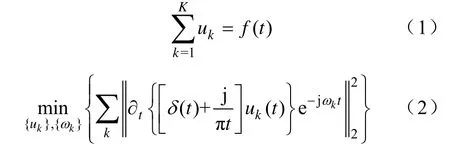
式中：δ(t)为脉冲函数；∂t为函数对t求偏导数。

2）利用拉格朗日公式将上述优化问题转化为非约束性变分问题，并引入二次惩罚项增强函数的收敛性，即

式中：α为惩罚因子；λ(t)为约束项。

3）应用交替方向乘子法，按式（4）和式（5）迭代求取上述最小优化问题。

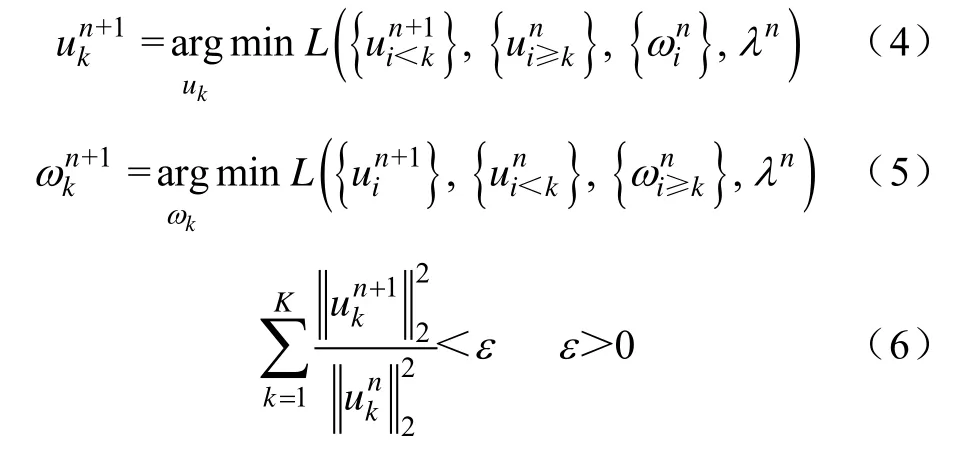
式（6）为上述迭代的收敛条件，ε为收敛的精度。

4）利用傅里叶变换求解式（4）和式（5）的频域解即当前信号的各模态分量与对应的中心频率，即

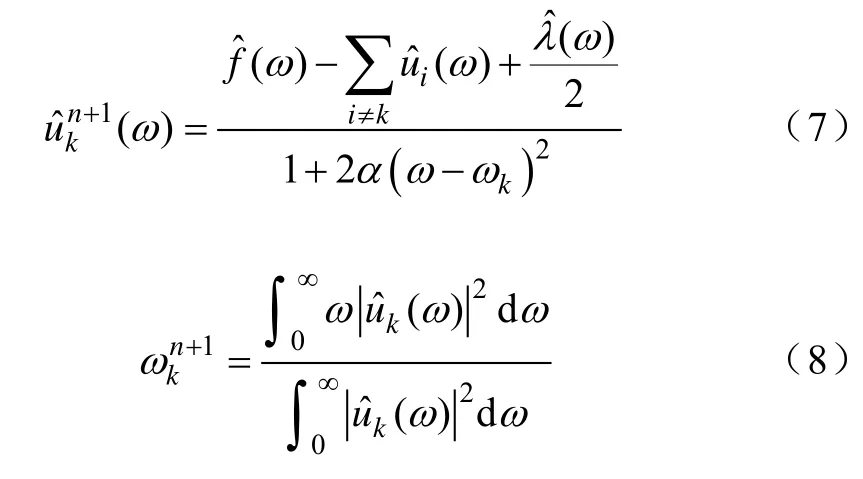
1.2 峭度

故障零序电流信号经VMD后能够得到若干个本征模态分量，为选取故障突变程度最显著的模态分量，引进峭度的概念。

峭度是信号的四阶平均值，属于无量纲参数，其值越大则表示突变的程度越高，更有利于提取故障特征。

式中：Ku为峭度；x为一组信号；μ、σ分别为信号的统计均值与方差。

分别计算200组HIF、100组负荷投切（load switching, LS）与100组电容器投切（capacitor switching, CS）事件的零序电流的峭度均值，见表1。结果表明，IMF2在三种事件中的峭度值均为最大，因此选用IMF2作为故障特征的图信号。

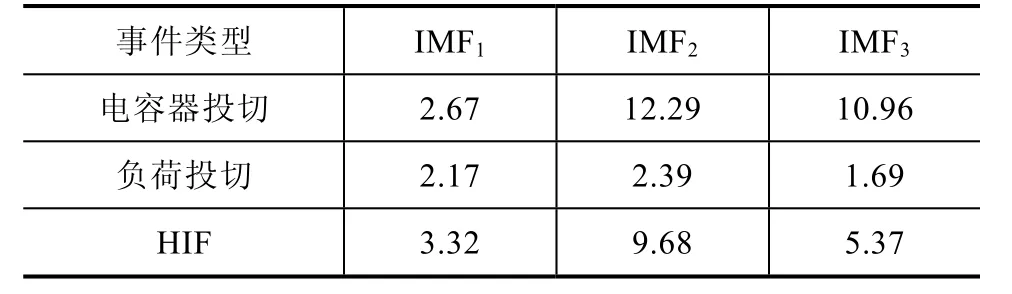
表1 各本征模态分量对应的峭度均值

1.3 图信号指标

由于本征模态分量由若干个相邻离散点连接构成，因此，本征模态分量可当作无向图。设模态分量由n个点{x1,…,xn}与m条边构成，其中连续的两个点构成一条边，即m=n+1条。

1）求取该模态分量中各条边的权值ijω并赋予对应的邻接矩阵W。

式中：h可根据两点之间的距离大小人为选定，此处取0.01；ix、xj为两个相邻点。

2）求取度对角矩阵D，其元素为

3）求取拉普拉斯矩阵L，即

4）求取拉普拉斯矩阵L与邻接矩阵W的所有特征值，即

式中：zi、iy、iλ、iμ为L与W对应的特征向量与特征值。

5）得到图的邻接矩阵谱σ(W)={λ1,λ2,…,λn}与拉普拉斯矩阵谱σ(L)= {μ1,μ2,…,μn}，即

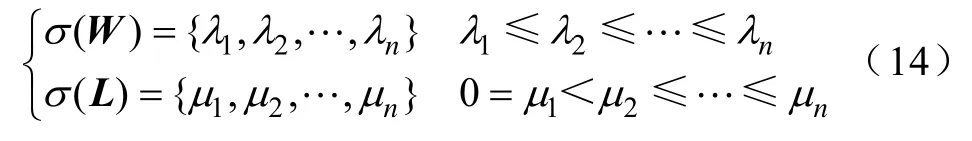
6）计算常见的五个图信号指标，分别为图能量指标（S1）、Estrada指标（S2）、拉普拉斯能量（S3）、拉普拉斯Estrada指标（S4）、类拉普拉斯能量不变量（S5），则有

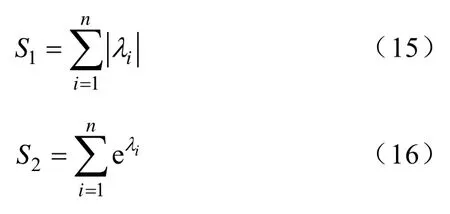
1.4 随机森林

随机森林是分类回归树的集成算法，其本质是基于基尼指数的二叉决策树，它可以同时处理离散型数据和连续型数据。决策树具体的构造过程如下：

1）采集所需要的样本保存为样本库D，并计算其基尼指数，即

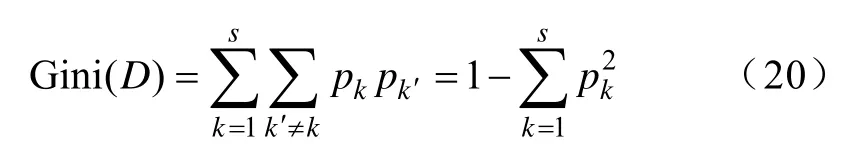
式中：pk为第k类样本占样本库D的比例；pk′为非第k类样本占样本库D的比例；s为样本库中的样本类。显然，Gini值越小则表示第k类样本在样本库的占比越大。

2）计算根据特征v所划分的样本v D的基尼指数为

式中：V为样本的特征数量；|D|为样本库的数量。

3）根据第2）步得到的不同特征下划分样本的基尼指数，得到最敏感的特征（即基尼指数最小），以此构建决策树树枝。

4）去除已使用的特征，重复步骤2）和步骤3），满足所有树枝下的数据类别均一致或所有特征使用完毕时，则决策树构建完毕。

随机森林与决策树构建不同的地方在于它在步骤2）任意选择V个特征中的a个（a＜V）进行多个决策树的建立，而不是一次性遍历所有特征，这使得它较决策树具有更好的泛化能力。

随机森林特征重要性评估：

1）设随机森林共有b棵决策树，当第i棵决策树的树枝j分裂到树枝l、r时，得到特征v在树枝j分裂前后的基尼指数变化量Pivj，即重要性为

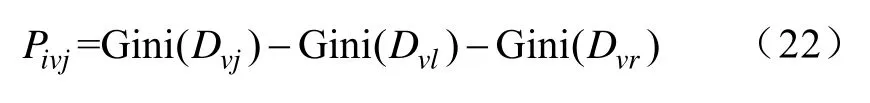
式中，Gini(Dvj)、Gini(Dvl)、Gini(Dvr)分别为在树枝j根据特征v所划分的样本基尼指数。

2）设特征v出现在第i棵决策树的c根树枝，得到特征v在第i棵决策树的重要性Piv为

3）求特征v对随机森林重要性即b棵决策树的特征重要性之和vP为

4）将V个特征的重要性进行归一化处理得到重要性评分IMPv为

2 故障识别算法流程

利用VMD与图信号指标提取故障时零序电流的特征，并通过随机森林进行特征重要性评估，选取重要性评分最高的特征，再通过随机森林分类器进行分类。识别算法流程如图1所示。具体步骤如下：

图1 识别算法流程

1）信号采集。采集仿真线路上发生HIF、电容器投切和负荷投切事件下的零序电流，截取故障前一个周波与后三个周波作为样本。

2）特征提取。通过VMD得到三个本征模态分量（IMF1、IMF2、IMF3），再计算对应的峭度，选取峭度值最大（对突变最敏感）的模态分量（IMF2），并计算对应的五个图信号指标。

3）特征重要性评估。通过随机森林算法选取最敏感的前三个指标作为故障特征。

4）故障分类。通过随机森林分类器对故障特征进行分类。

3 仿真与验证

3.1 HIF模型

以往已经提出多种HIF模型，例如Mayr、Cassie、Schwarz及控制论模型[16]。这些模型虽然能够模拟故障电流的多种特性，但也引入了数个复杂的微分方程，这不利于仿真模型的搭建与运行。因此，选用根据现场实测数据搭建的Emanuel模型。该模型通过控制两个电阻的阻值来模拟故障电流的半周期不对称性，通过两个反并联二极管与直流电源串联来模拟故障电流的零休特性。Emanuel模型如图2所示。

图2 Emanuel模型

由于在配电网实际运行中，故障线路可能同时接触不同的故障表面，因此Emanuel模型也衍生出并联形式[14]，如图3所示。该模型通过设置直流电源幅值、电阻的大小及开关通断时间来模拟多重故障电流混合的效果，同时也可模拟故障电流的累积效应、肩峰特性、间歇性与不对称性等。该模型的参数设置见表2。

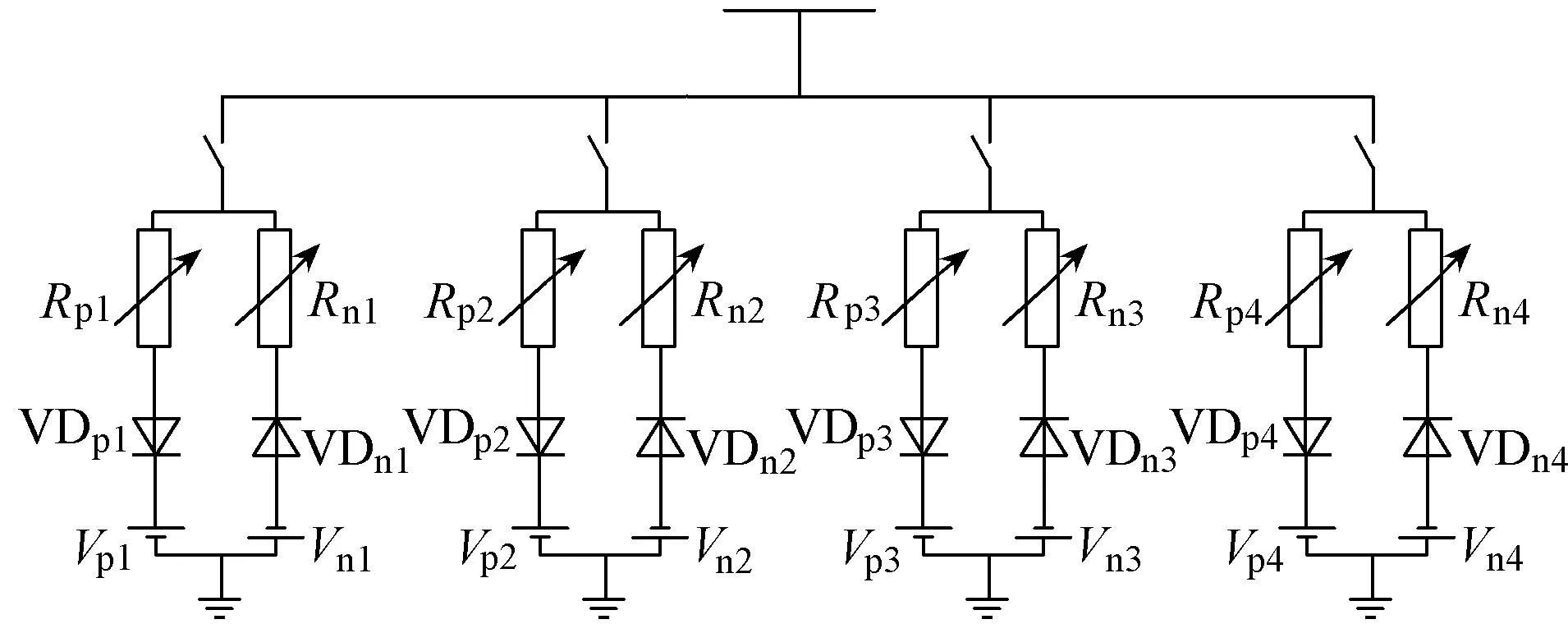
图3 并联Emanuel模型

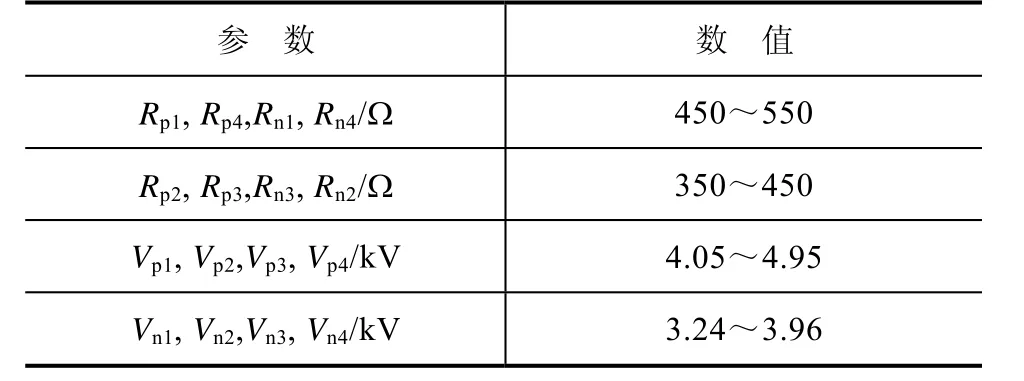
表2 并联Emanuel模型参数设置

3.2 10kV配电网模型

在PSCAD/EMTDC中，建立一个10kV辐射型配电网模型，如图4所示。线路参数见表3。选用图3中并联Emanuel模型，故障初相角设置为0°、60°、90°、120°。

图4 10kV配电网模型

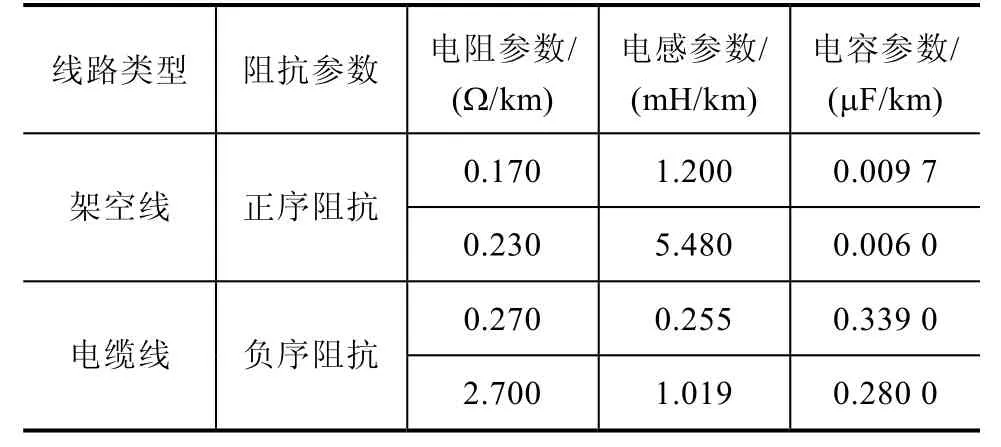
表3 配电网模型线路参数

线路l22发生HIF、电容器投切（CS）、负荷投切（LS）时，母线采集的零序电流如图5（a）～图5（c）所示。可见，发生高阻接地故障时，零序电流产生突变，并具有明显的零休与半周期不对称性，随着时间累积，电流幅值会增长到一个极大值。发生CS时，线路上大量高频分量导致零序电流产生突变。投入不平衡负荷时，瞬时高频分量使零序电流产生暂态突变，之后回到稳定状态。

通过VMD提取图5（a）～图5（c）的IMF2分量，如图5（d）～图5（f）所示。发生HIF时，IMF2会产生持续的突变，并在某一时刻达到最大值。而LS、CS发生时，IMF2突变仅发生在事件初期暂态时刻，之后回到稳定状态。

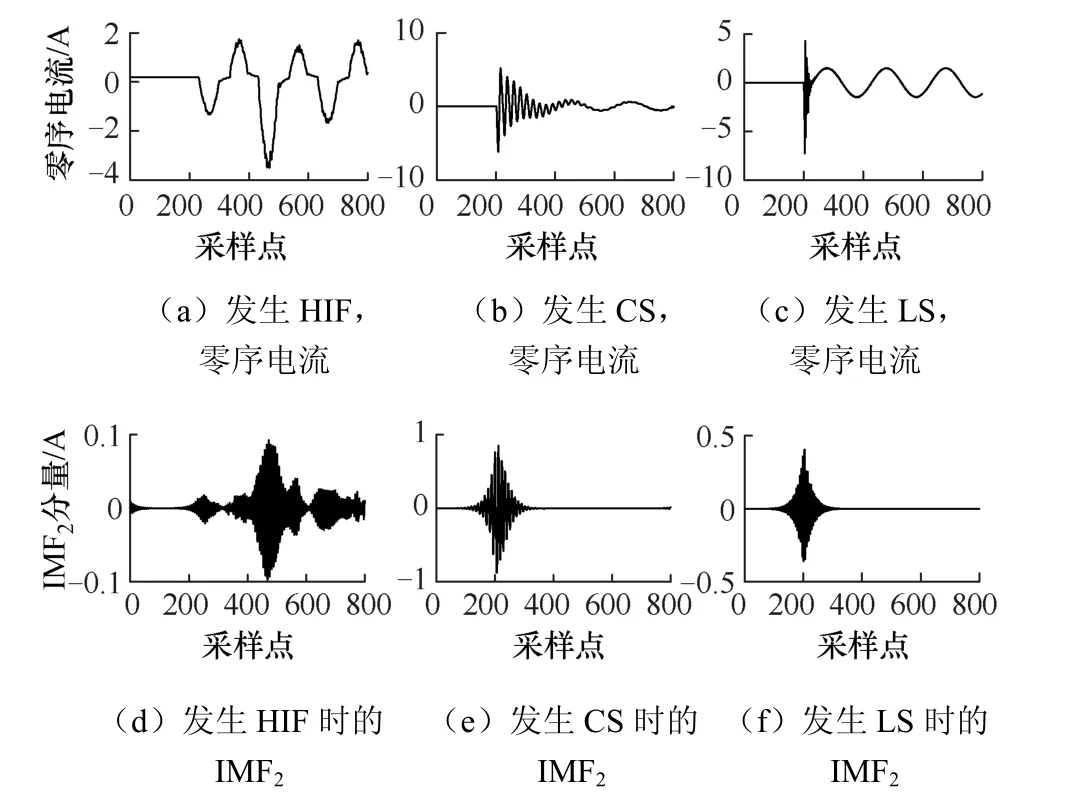
图5 HIF、CS、LS的零序电流与对应的IMF2

基于上述不同事件下IMF2图结构的差异，选用图信号指标作为故障特征。首先，采集200组HIF，100组CS和100组LS的零序电流作为样本库，随机选取70%用于训练，30%用于测试；其次，通过VMD得到零序电流的IMF2分量，并求取对应的五个图信号指标；接着，通过随机森林算法对指标进行特征重要性评估，其结果见表4；最后，选择S2、S3、S5作为故障特征输入随机森林分类器进行分类，测试准确率高达98.33%。

表4 图信号指标重要性评估结果

考虑噪声对所提算法的影响，上述测试样本叠加信噪比为30dB的高斯白噪声，对应的信噪比为30dB时的零序电流与IMF2如图6所示。对比图5（d）～图5（f）与图6（d）～图6（f）可知，LS与CS的IMF2突变仍然仅出现在投切事件的初期，而HIF的IMF2突变在故障持续期间一直存在。最后，通过随机森林分类器对该组噪声测试波形进行测试，准确率仍高达96.67%。

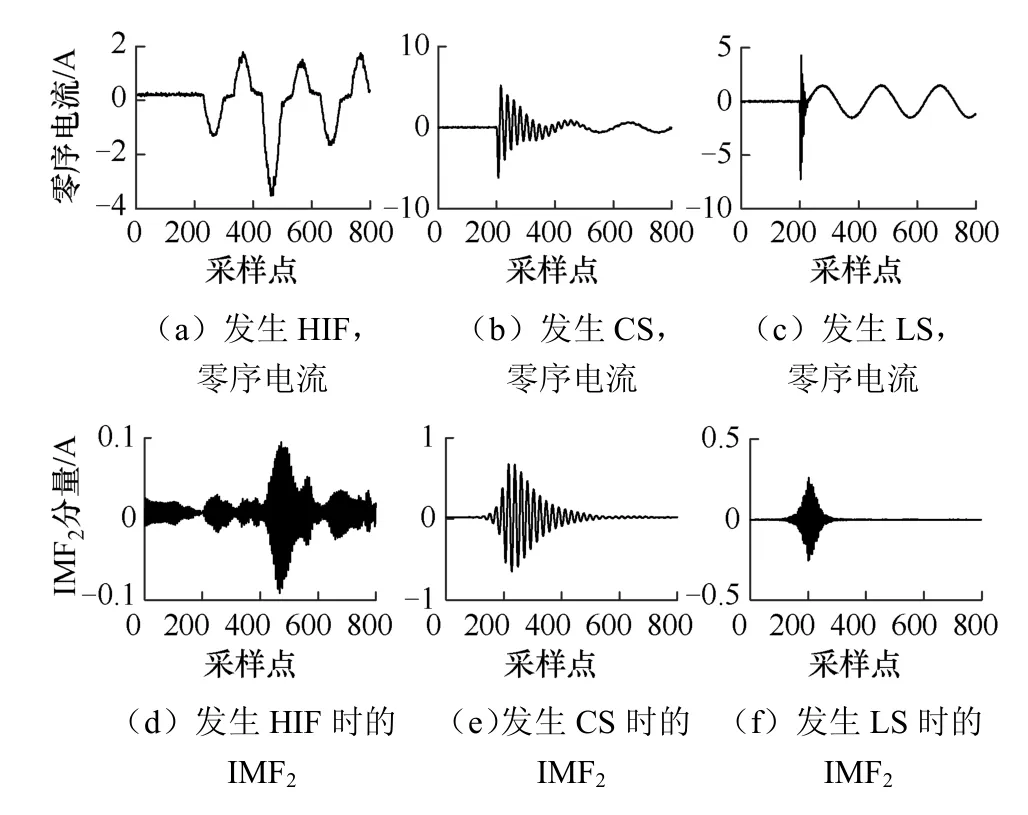
图6 信噪比为30dB时的零序电流与对应的IMF2

4 结论

基于配电网发生不同事件时，本征模态分量图结构之间的差异，本文提出了一种结合VMD与图信号指标的HIF检测算法。经过PSCAD/EMTDC的仿真测试及噪声干扰测试，得到以下结论：

1）图信号指标能够区分不同的本征模态分量。

2）所提算法能够区分HIF、负荷投切与电容器投切。

3）该算法具备抗噪能力，在信噪比为30dB的噪声干扰下，仍保持较高准确率。