考虑蓄电池储能的配电网动态网络重构

谢亮，李远卓，崔慧军，宋庆昌，罗欣，张志伟

（1.国网冀北电力有限公司，北京100085；2.北京清软创新科技股份有限公司，北京100085）

0 引言

具有间歇性和波动性的分布式电源（distributed generation，DG）由用户侧大量接入电网，使得用户侧负荷波动变大。同时蓄电池储能（battery energy storage，BES）技术逐渐成熟，成本的下降使其削峰填谷效益越来越明显，在一定程度上改善了负荷波动情况［1—2］。对于电力公司特别是调度部门来说，要根据历史负荷情况准确预测未来网络最佳结构，在制定调度运行策略中具有重要作用［3—4］。

目前，有关配电网重构技术的研究主要分为2大类，第一是以节点和支路重要程度为依据的网络重构；第二是以网损、电压偏移量等性能指标为目标建立数学模型的网络重构。

文献［5］通过评价节点和支路的重要程度，提出一种基于Hadoop平台的分布式粒子群算法，对大规模网络进行高效率的重构。文献［6］提出一种节点重要度的新评价方法，并建立了双层优化模型，该模型以最大化系统可用发电容量确定发电节点恢复顺序、以最大化恢复路径的平均重要度和最小化路径的充电电容为目标，确定恢复路径。文献［7］利用节点收缩后的网络凝聚度定量评价网络中电源和负荷的重要性，进而提出一种基于节点重要度评价的骨架网络重构策略。文献［8］考虑了具有间歇性的DG和负荷的多状态，建立了含DG的配电网动态重构机会约束规划模型。文献［9］从配电重构本质出发，建立考虑网损和载荷均衡的多目标网络重构模型。文献［10］将网络损耗和电压偏移量作为衡量系统运行性能的指标，以二者归一化的综合指标为标准建立网络重构模型。文献［11］提出了含DG的配电网重构和检修计划优化，从一定程度上说明了检修计划对配电网重构的影响。文献［12］分析了检修计划对电网运行的影响，并提出了变电站计划检修时过负荷率以及减供负荷率的计算方法，将检修计划对负荷的影响具体化。

上述文献中考虑节点和支路重要程度的网络重构研究，多是在静态下进行的，面对实时变化的负荷值很难满足需求。以网损、电压偏移量等性能指标为目标更适用于动态网络重构研究，但现有文献中很少有考虑BES的网络重构研究。

本文在现有文献的基础上，考虑BES在配电网中的应用，研究动态下的配电网重构技术。以网络损耗最小为最终优化目标，根据负荷变化和BES充放电情况设定网络重构条件，并考虑网络拓扑结构、开关动作次数等约束条件，建立数学模型；将嵌入fmincon函数的遗传算法作为求解方法。最后通过算例分析验证本文所提方法的有效性。

1 BES的数学模型

本文从剩余电量水平（state of charge，SOC）和充放电功率等方面对BES进行数学建模。

充电过程时

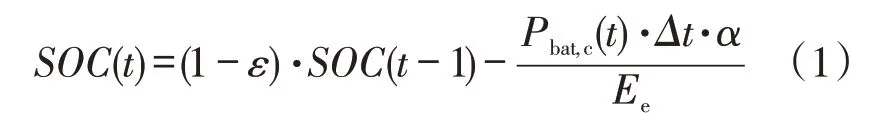
放电过程时

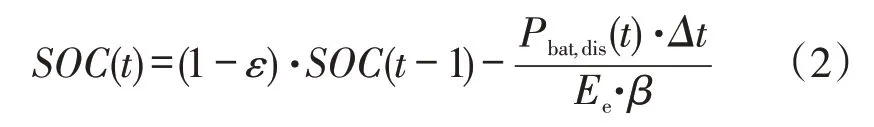
式中：SOC(t)为第t个采样间隔处BES的剩余电量水平；ε为BES剩余电量每小时的损失率，简称自放电率；Pbat,c(t)、Pbat,dis(t)分别为BES充、放电功率大小；α和β分别为BES充、放电效率；Ee为BES的额定容量；Δt为采样间隔，本文取1 h。

为避免电池过充过放，SOC有一定范围限制，BES不能将电量全部放完也不能完全充满。

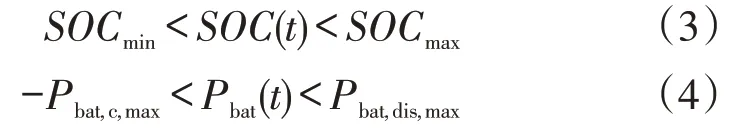
式中：SOCmin、SOCmax分别为电池最小剩余电量水平和最大剩余电量水平；Pbat(t)、Pbat,c,max、Pbat,dis,max分别为BES电功率、最大允许充电功率、最大允许放电功率，负号表示BES充电。

2 网络重构模型

由于配电网络中各节点的电压等级比较低，网损成为不可忽视的一部分。配电网络重构作为一项重要的配电网自动化技术，可以在不投入更多额外设备的情况下，仅对线路上开关的状态进行调整，就可实现降低网络损耗，改善电压质量的目的。本文将网络损耗最小作为网络重构最终的优化目标建立数学模型，并列出具体的目标函数和约束条件。

本文在动态网络重构中考虑BES，相应的重构模型建立时需要BES的运行过程；而BES运行策略的制定又是以网络结构为基础的。二者互相迭代才能计算，与双层优化模型相匹配。在双层优化模型中，上层优化结果作用于下层目标函数和约束条件，下层优化以最优值反馈到上层，实现上下层之间的相互作用。

2.1 上层优化数学模型

2.1.1 上层目标函数

优化的目标是在系统安全稳定的基础上实现网络损耗最小化，具体优化时分为静态优化和动态优化。动态优化目标函数为

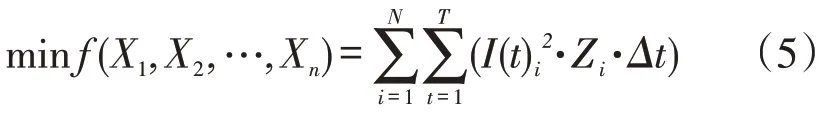
式中：X1,X2,…,Xn分别为配电系统中的n个开关状态量，是控制变量；N为系统中总的支路数；T为系统需重构的总的时间段；I(t)i为第i条支路在t时刻时的电流值；Zi为第i条支路的阻抗值。

对于静态优化，其为在单一时间断面上的优化，目标函数为

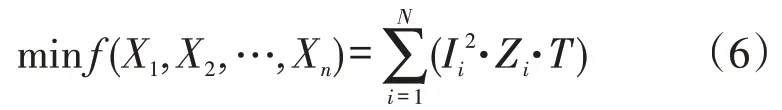
式中：Ii为第i条支路的电流值。

2.1.2 上层约束条件

无论是静态网络重构模型还是动态网络重构模型，都需要一定的约束条件，实现所求解的正确性，以及更加符合实际性。

（1）节点电压约束

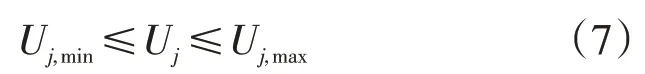
式中：Uj,min、Uj,max分别为第j节点处电压Uj的下限和上限；b为配电网节点总数(j=1,2,…,b)。该约束是电能质量对BES运行的要求。

（2）支路电流约束

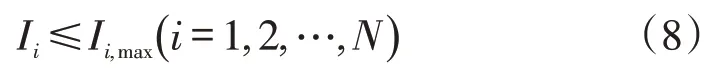
式中：Ii,max为第i条支路电流Ii的上限。该约束是系统安全稳定对BES运行的要求。

（3）潮流方程约束

式中：PG,i、QG,i分别为节点i处电源的有功和无功出力；PL,i、QL,i分别为节点i处的有功和无功负荷；Ui、Uj分别为节点i和节点j的电压幅值；Gij、Bij分别为节点导纳矩阵元素的实部和虚部；θij为节点i和节点j的电压相角差。

（4）配电网络拓扑约束

重构后的配电系统应满足辐射状拓扑结构的要求，无环网、孤岛形成。

（5）开关开断次数约束

考虑开关寿命问题，避免开关在一段时间内连续多次开断，保障其可靠性。即

式中：ST、ST,max分别为T时间段内某一开关的开断次数和最大开断次数。

2.2 下层优化数学模型

2.2.1 下层目标函数

优化的目标是经济效益最大，即

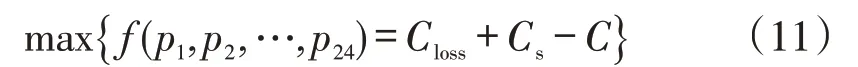
式中：p1,p2,…,p24为BES在24个小时段上的充放电功率（一个时间段内BES既可以充电也可以放电），是控制变量；Closs为BES运行后配电网降低能耗日收益；Cs为BES一天的低储高放套利；C为日周期内充放电次数大于一定值时的惩罚项。

各分量计算公式为

式中：Ploss(t)为在第t个采样间隔内配电网的有功线损；ma为配电网从主网购电电价；h为电池一日中的充放电次数（将一个充电阶段加上一个放电阶段算做一次充放电）；hmax为一日中的充放电次数限制值；γ为惩罚系数；Cs,dis、Cs,c分别为BES一天的放电收入费用和充电支出费用。

计算公式如下

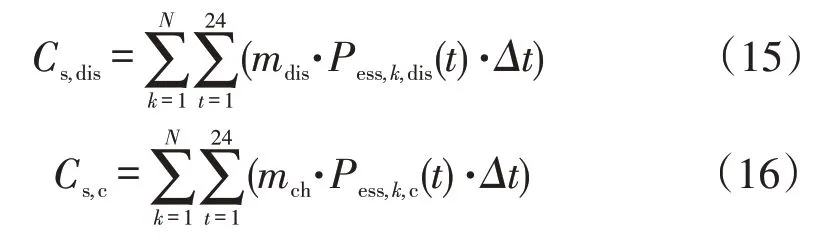
式中：k为BES类型；N为BES的个数；mdis、mch分别为BES放电电价和充电电价，都为对应时段处的分时电价；Pess,k,dis(t)、Pess,k,c(t)分别为BES在t时刻的放电功率和充电功率（负数表示充电、正数表示放电）。

2.2.2 下层约束条件

下层约束条件除了和上层约束中的式（7）—式（9）一样外，还有充放电功率约束。即

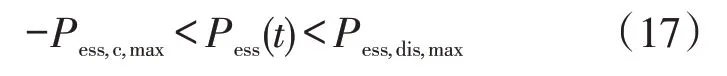
式中：Pess(t)为BES各小时段处的充放电功率；Pess,c,max、Pess,dis,max分别为电池最大允许充电功率和最大允许放电功率，负号表示电池充电。

3 算例分析

3.1 算例描述

为验证本文所提方法的有效性，以修改的IEEE33节点配电系统［13］作为算例，系统结构如图1所示。其中虚线为联络线，联络线参数参考其他支路设置，如表1所示。节点15和节点28上分别配有容量为420 kWh和562 kWh的BES。BES位置和容量参照文献［13］与文献［14］进行确定。参考文献［15］设定分时电价，高峰时段：9:00—14:00和19:00—21:00，电价为1.0元/kWh；低谷时段：1:00—8:00，电价为0.35元/kWh；其余时段的平时段电价为0.55元/kWh。从主网购电电价为0.55元/kWh。某地典型日负荷曲线如图2所示。日充放电次数最大值为3。

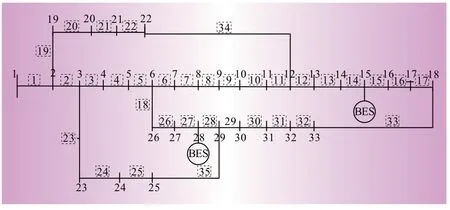
图1 配电网算例系统图Fig.1 System diagram of distribution network example

单个蓄电池储能单元（1 kWh）最大充、放电功率均为0.5 kW。对于SOC的上下限，实际工程中考虑了储能的寿命问题，一般取80%和20%；本算例为突出BES运行后的经济效益，其上下限分别取90%和10%。充、放电效率均为95%，剩余电量损失率为10%。SOC初始值设置为10%。电压波动上下限为±7%。支路电流上限取静态运行时支路电流的1.5倍。单个开关日开断次数最大值为3。遗传算法中进化代数为30，种群规模为50，交叉率0.6，变异率0.01。

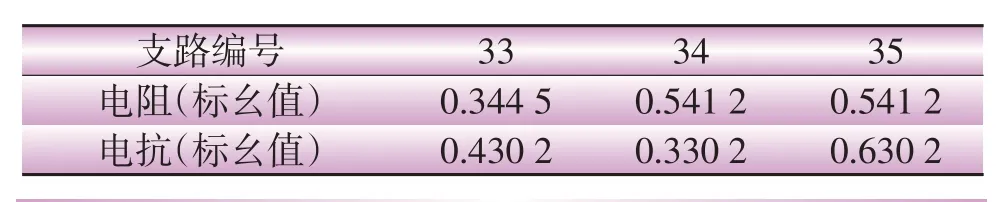
表1 联络线参数表Table 1 Tie line parameter table

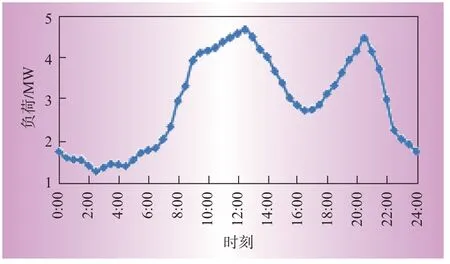
图2 典型日负荷曲线Fig.2 Typical daily load curve

3.2 求解方法

本文通过嵌入fmincon函数的遗传算法对双层优化模型进行求解。该函数对初始值的选择无任何要求，收敛速度快，使用简便，结果准确。其中fmincon函数求解下层BES运行策略，遗传算法计算上层网络重构结果。

3.3 算例分析

静态网络重构、动态网络重构结果如表2所示，其中静态网络重构时各节点负荷为动态网络重构时节点负荷的日平均值。

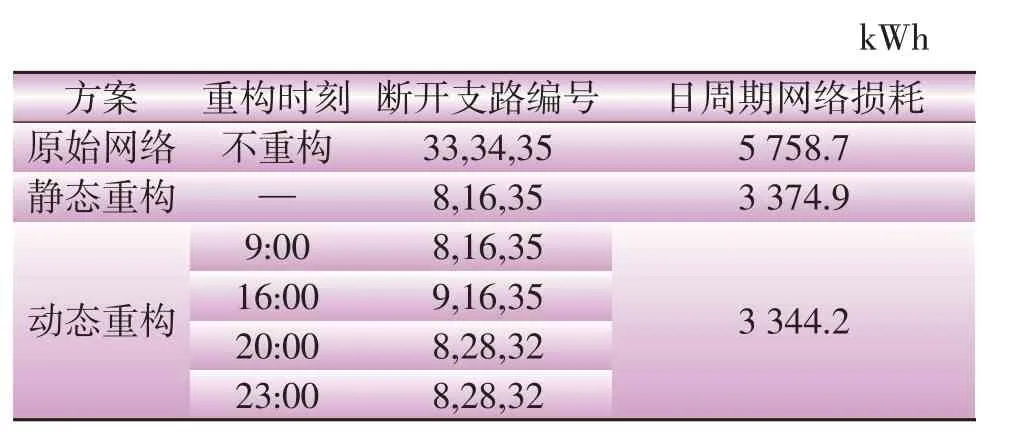
表2 网络重构结果Table 2 Network reconfiguration results

从表2中可以看出9:00时动态网络重构结果与静态网络重构相同，23:00时动态网络重构结果与20:00时相同；静态重构后周期内的网络损耗较原始网络少2 383.8 kWh。在考虑负荷变化的动态重构中，9、16、20和23时都满足重构条件进行重构，但9:00重构结果与静态重构结果一致，23:00重构结果和20:00重构结果一致，因此开关开断次数为3次，满足动作次数约束条件。动态重构后的周期内网络损耗比静态时少30.7 kWh，说明在同时满足一定约束条件下动态重构优于静态重构。

BES运行前、后的负荷曲线如图3所示，考虑BES运行的网络重构结果如表3所示。BES日经济效益为609.1元，其中低储高放套利559.5元，降低能耗收益49.6元。

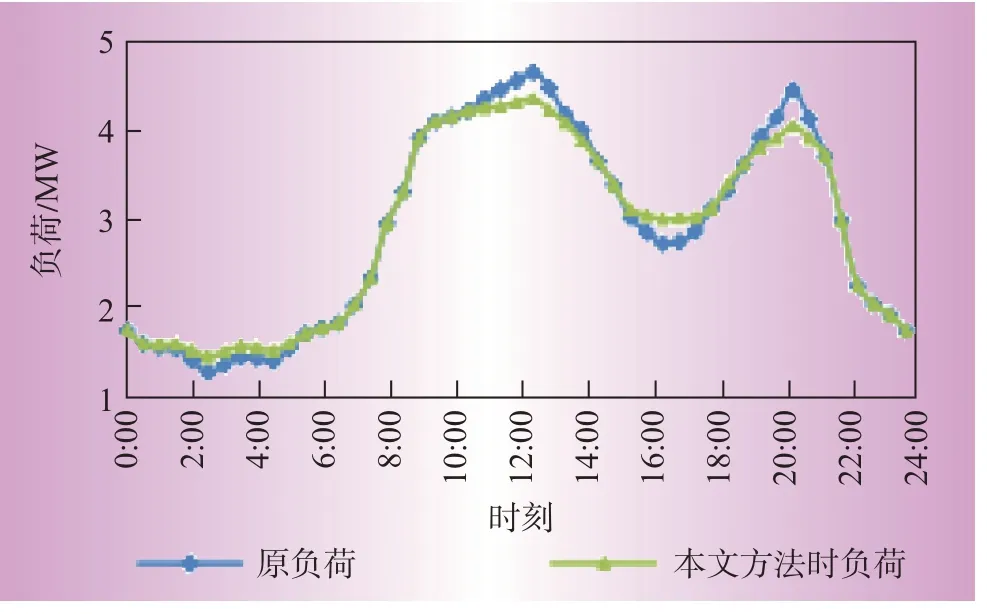
图3 BES运行前后的负荷曲线Fig.3 Load curves before and after BES operation

表3 考虑BES的网络重构结果Table 3 Network reconfiguration results considering BES

由表3得考虑BES运行的动态网络重构日损耗比静态网络重构少20.1 kWh。对比表3和表2可以看出，考虑BES运行的静态网络重构比不考虑BES时降低损耗97.8 kWh；考虑BES运行的动态网络重构比不考虑BES时降低损耗90.1 kWh，且重构次数由3次减少为2次，重构时间由9:00、16:00、20:00和23:00变为12:00、20:00。

BES优化运行后的负荷曲线波动相对平缓，网络损耗变少，验证了BES削峰填谷的能力。相比原负荷变化情况，考虑BES运行的网络动态重构会因负荷曲线相对平缓而减少重构次数，避免开关长期多次切换。

4 结束语

本文考虑BES的实际运行情况，研究动态网络重构方法，通过算例分析表明：

（1）利用本文方法，在满足拓扑结构、开关切换次数等约束条件下，动态网络重构日周期内网络损耗小于静态网络重构。

（2）BES合理的充放电策略可以对负荷进行削峰填谷，减少网络损耗，具有一定经济效益。

（3）考虑BES运行的动态网络重构时，BES运行策略与网络重构策略可以相互作用，共同实现网络运行最优化。