V63夹紧器下盖的设计与结构优化

范磊， 梅驷俊， 宗晨

（1.上海德珂斯机械自动化技术有限公司，上海201802 2.上海振华重工（集团）有限公司，上海200125）

0 引言

Tuenkers在20世纪70年代就获得了肘节闭锁功能的夹紧器专利，也是因为这项发明，为众多的全自动系统提供了方案。如图1所示，夹紧器在白车身焊装车间有广泛的应用，用于夹紧车件于固定工作台、移动滑撬或者抓具上。

图1 夹紧器在白车身焊装车间的应用案例

夹紧器的工作原理：通过上下腔体中气体带动连杆机构来实现对车件的夹紧与松开。如图2所示，下腔体进气，上腔体出气，气压推动活塞向上运动，活塞杆带动连杆，最终，转动轴来带动夹臂的夹紧；反之，下腔体出气，上腔体进气为夹紧器的打开过程。打开过程中，下腔体气压及活塞运动到底部对夹紧器下盖产生冲击，使用不当或超过一定循环次数后，下盖容易出现断裂的情况，如图3所示。汽车白车身焊装车间对由于生产设备维修而导致停线、停产时间有很严格的控制，因此对于设备、产品的强度、可靠性提出了更高的要求。本文以V63夹紧器产品为研究对象，分析下盖的断裂原因，通过拓扑优化法改善其结构和疲劳寿命。

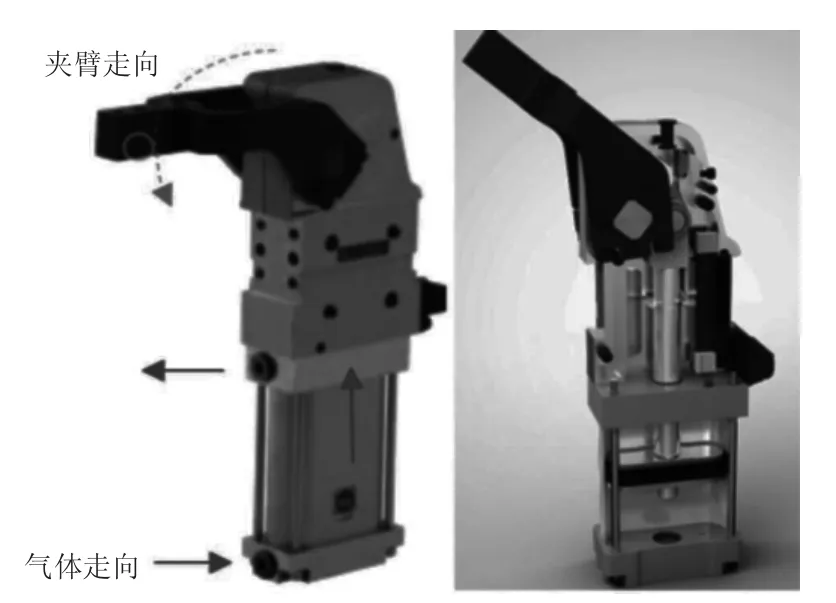
图2 V63夹紧器的工作原理

1 计算模型的建立

利用SolidWorks软件，按1：1建立模型，并进行静力学强度分析，材料定义为356.0-T6永久成型铸件（SS）,密度为2680 kg/m3,弹性模量为72.4 GPa，屈服强度为152 MPa,抗拉强度为228 MPa，延展性为1.086%。

2 边界条件和负载加载

2.1 约束

图3 V63夹紧器下盖断裂

由图2可知，下盖是通过四角4颗长螺栓与腔体扁钢、上盖固定在一起的。所以，本文中的螺栓安装面定义面约束，4个通孔定义为仅释放Z向旋转自由度。

2.2 负载

按照产品样本，夹紧器定义了两种使用方式：循环周期为1 s和2 s，负载为产品手册上定义的最大负载，如图4所示。另外，气缸的标准使用气压为0.5 MPa。作用在下盖上的力的计算，因为涉及不同的负载、循环时间、缓存效果，是一个复杂的气体动力学问题，需要通过实验来核实，不作为本文的讨论重点。本文仅应用经验及实验结论，取加载力F=14400 N，作用面为下盖的整个内凹槽面。

3 应力及疲劳寿命仿真结果与分析

3.1 应力仿真结果分析

Von Mises应力如图5所示；由图5应力分析可知，最大应力值为57 MPa,小于材料的屈服强度，满足静强度的要求。

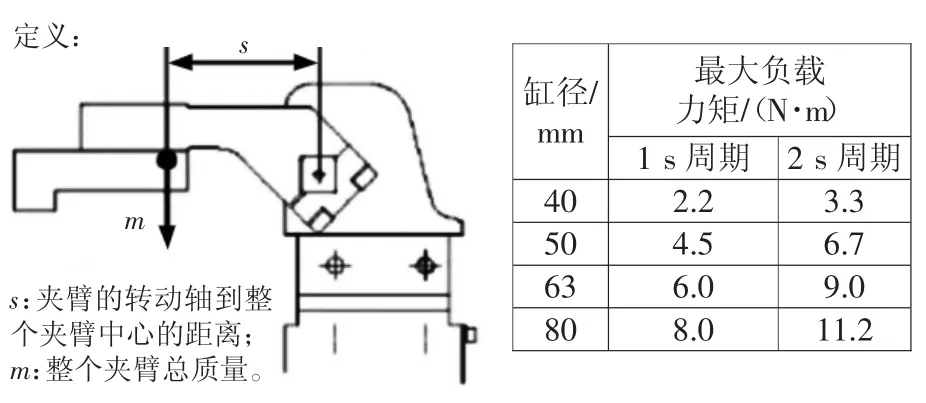
图4 许用最大负载力矩

图5 应力图

3.2 疲劳寿命校核理论[1]

疲劳失效以前所经历的应力或应变循环次数称为疲劳寿命[2]，即应力循环总周期数。而导致失败所需的应力周期数实际上是无穷大，即为无限寿命。为了充分利用材料的承载能力并且减轻结构的质量，而产生了有限寿命设计准则[3]。陈科等[4]遵循有限寿命设计方法，并按照文献[5]进行理论疲劳强度校核。累积损伤规律是疲劳研究中最主要的方法，它是估算变幅载荷作用下结构疲劳寿命的基础，Miner（迈因纳法则）线性累计损伤理论形式简单，使用方便，是目前普遍的疲劳寿命预测方法。基于Miner理论的基本假设[6]，通过测量各级应力的频次与零件S-N曲线上的理论频次之比的累积值就得到零件的损伤量。若试件受到σ1，σ2，…σn，等n个不同级别应力的作用，试件在各级应力级别下的理论寿命分别是N1，N2，…Nn，而各级应力级别下的实际循环数为n1，n2，…nn，,则应力级别σi的损伤分量为[7]

由公式（1）可得，该试件每个循环的总损伤为

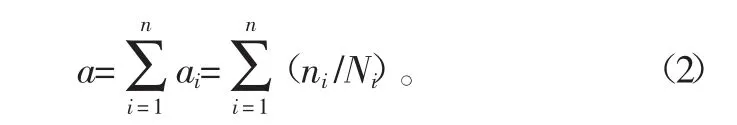
则该试件可以承受的总周期数为

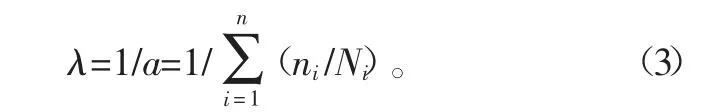
则该试件的疲劳寿命为

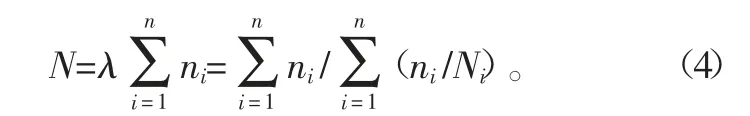
3.3 疲劳分析算例

本文使用SolidWorks中的疲劳分析模块，疲劳寿命如图6、图7所示。

图6 改进前损失百分比

图7 改进后生命周期

SolidWorks中疲劳分析设定如下：基于ASME碳钢曲线，应用双对数差值法，从材料弹性模量派生疲劳S-N曲线。恒定振幅随意事件交互作用，用对等应力（Von Mises）计算交替应力，用Goodman纠正平均应力（因为Goodman方法通常适合于脆性材料），疲劳强度缩减因子为1，无限生命。

SolidWorks 中的疲劳结果，根据上述的Miner 及Goodman[8]等理论不难理解。

由图6可知，该事件中下盖的最高损伤百分比是29.92%，损伤比比较高。

由图7可知，下盖的疲劳最薄弱点出现在下盖前后两条纵向筋的端部，这与现实中下盖断裂口裂纹处一致。

4 拓扑优化与尺寸优化

优化设计的过程是建立准确的优化模型，设定优化变量和优化目标，采用合适的优化算法，通过迭代计算，得到最优设计方案[9-10]。本文选用SolidWorks中的Intel Direct Sparse自动解算器，运行静态分析，然后再运行拓扑算例（如图8），算例设定以最佳强度质量比为目标，减少30%质量为质量约束，1.2×最大尺寸模型位移为位移约束，并且控制最小构件厚度为3 mm。

通过拓扑算例结果，通过确定移除的质量（如图8中深颜色显示），指导模型部分关键尺寸优化，如表1所示，下盖的静强度、疲劳强度均有所提高，而且质量仅增加（214-200）÷200=7%，实现了应力降低（57-30）÷57=47%。同时，表1中A1尺寸考虑了脱模方便性，表1中T1、T2、D3、D4保证铸液更好的流动性，增大铸件最小壁厚（如图9亮显的最小壁厚危险面），而进一步保证铸件毛坯质量，降低后续的多道提升质量工艺成本，如铸件表面浸渗。

如表1所示，优化后Von Mises为30 MPa,位移为0.025 mm。如图10、图11所示，优化后该算例中，下盖可达无限寿命。结构优化方法方面，除了SolidWorks拓扑优化，还可以使用ANSYS Workbench 的多目标遗传算法，Von Mises、合位移及质量最小为目标，得到多个最优解，范磊等[11]详细讲述了方案。

图8 拓扑算例结果

图9 最小壁厚危险面

图10 改进后损坏百分比

图11 改进后生命总数（周期）

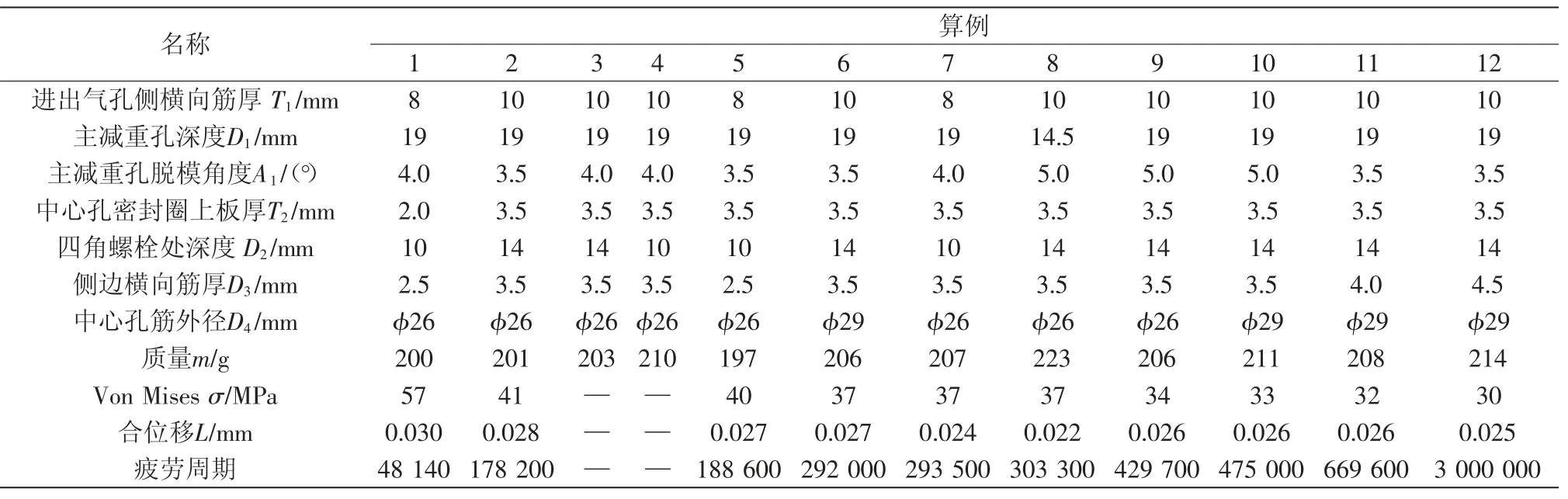
表1 拓扑优化过程

5 结论

以V63夹紧器产品中易断裂的下盖为研究对象，利用SolidWorks软件建立铸造件下盖模型，通过拓扑优化法结论来指导尺寸优化，同时考虑铸造工艺，采用了有利于脱模效果、铸液流动性等的尺寸因素。最终实现仅增加质量7%，而应力降低47%。并且通过反复多次的疲劳分析及改进，确认该下盖已能达到无限寿命设计要求，满足于产品定义的3 000 000次的循环寿命。