机械设计手册一组力学公式的探讨

周治，赵家乐，胥正皆

（1.重庆天辰精工科技有限公司，重庆402760；2.重庆伊士顿电梯有限责任公司，重庆401336）

0 引言

机械设计手册作为机械行业广泛使用的工具书，具有权威性、准确性、实用性，所选内容基本、常用、重要，工程技术人员工作中参考它可提高机械设计制造质量和效率，使用者往往对机械设计手册中给出的数学公式、物理公式、力学公式、设计方法深信不疑。因此，如果机械设计手册一旦有错误，使用者一般也会随之出现认知上的错误，从而给设计制造带来失误。

直线导轨与滑块广泛地运用于夹具、机器设备，尤其是在自动化设备中，机械设计手册给出了常见的四滑块工作台直线运动载荷计算公式。图1为四滑块工作台载荷受力图[1]。文献[1]给出的使用条件是：工作台水平使用（滑块运动），匀速运动或静止时，外加载荷W不与工作台中 心 重 合；P1、P2、P3、P4分别为4个滑块A、B、C、D因工作台外加载荷W所导致受到的压力；假设台面是刚体，工作台质量不计。文献[1]给出求解P1、P2、P3、P4值的公式如下：

图1 四滑块工作台载荷受力图

与文献[1]载荷计算公式相同的还有文献[2]～文献[4]。另外与文献[1]载荷计算公式本质相同的还有文献[5]、[6]，文献[5]、[6]只是再考虑了工作台质量；在忽略工作台质量的情况下,文献[1]及文献[5]、[6]载荷计算公式是一致的。

例1：在图1中，设取l0=1500，l1=900，l2=500，l3=300，W=2400 N，试计算P1、P2、P3、P4受力大小。

将已知数据代入式（1）～式（4）求得：P1=600 N，P2=-200 N，P3=600 N，P4=1400 N。

其中P1、P3、P4为正值，其物理意义说明外加载荷W确实引起了由工作台向对应处的滑块A、滑块C、滑块D的压力；而P2为负值,其物理意义说明外加载荷W在滑块B处引起了一个由滑块B向工作台的力，对此，从生活经验及力学知识来说是不能理解的。

同时，笔者工作经历中曾设计汽车检测中的整备质量设备，其受力模型与图1一致，对应于滑块A、B、C、D处安装有重力传感器，所测得P1、P2、P3、P4的值与按公式（1）～式（4）计算所得也相差甚远，这就让笔者怀疑文献[1]～[6]中相应载荷计算公式的正确性。

本文按图1中文献[1]所给出使用条件，对求P1、P2、P3、P4的公式进行简单推导，并通过Creo5.0有限元分析，依据例1中的已知数据进行验证，从而说明其正确性。

1 公式推导

1.1 公式理论推导

在图1中，设滑块A、B、C、D的中心点分别为点A、B、C、D，因此，可设点A、B、C、D分别为滑块的集中受力点；在图2中便以此表示滑块而使得图形表达更清晰，对应滑块 受 力 为P1、P2、P3、P4。四滑块工作台施加外加载荷W后处于平衡状态，现可将外加载荷W按图2转化，可先将W转化成分别位于点C、D连线边上的P5力及点A、B连线上的P6力，其受力方向由工作台指向滑块，而P5、P6的大小遵循杠杆原理：

图2 工作台外加载荷W转化图

再把P5转化成P3、P4，而P3、P4的大小也遵循杠杆原理：

由式（5）、式（6）可解出：

与推出P4同理，有：

将例1中的已知数代入式（7）～式（10），可求得：P1=333.33 N，P2=66.67 N，P3=333.33 N，P4=1666.67 N。

1.2 公式简化表达

式（7）～式（10）表达较复杂，不便记忆与运用。

图3为滑块载荷计算面积比图。今将工作台过外加载荷W作用点处，作分别平行于连线AB、连线AD的平行线，则将工作台上由点A、B、C、D为四角顶点构成的大矩形分割成4个小矩形，如图3所示。它们的对角线 分 别 为WA、WB、WC、WD，对应地分别 用SWA、SWB、SWC、SWD表示各小矩形的面积，用SABCD表示工作台上矩形ABCD的面积，则有：

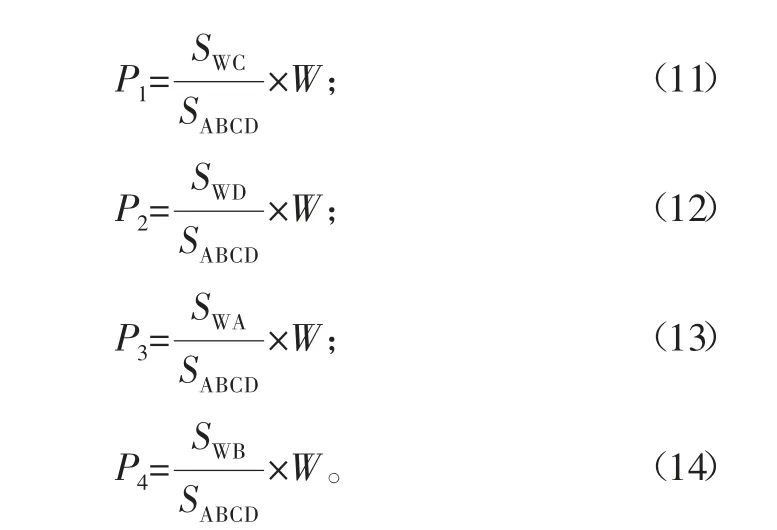
载荷计算公式（11）～式（14）本质上与式（7）～式（10）一样，但式（11）～式（14）表达简单、容易记忆、直观性强。

需注意：当外加载荷W施于矩形ABCD的边上时，则矩形ABCD被分割成的4个小矩形中相应的矩形退化成直线的情形，其面积为0。

2 Creo5.0分析验证

2.1 Creo5.0分析要点及注意事项

按例1中的已知数据，通过Creo5.0进行建模分析。分析过程中要充分体现几何建模的形似，有限元分析时体现神似，这样才能确保分析结果准确。

在Creo5.0分析中，进行材料定义时，为体现桌面是刚性的,文中弹性模量取值为2.1×109MPa,而非钢材的一般取值2.1×105MPa，如图4所示。

为体现4个滑块A、B、C、D支承工作台，对点A、B、C、D进行图6所示的约束。通常实体之全约束是对实体面进行X、Y、Z三个方向的平移约束;而此处对工作台上代表滑块的A、B、C、D四个点进行6个自由度的约束。在图5中，工作台面为Y、Z坐标轴所在平面，工作台面的法向为X轴，现对D点进行X、Y、Z三个方向的平移约束，对A点进行X、Z方向平移约束，对B、C两点进行X方向约束。在滑块A、B、C、D上建立对应于载荷公式（7）～式（10）计算所得的P1、P2、P3、P4测量点。

图4 材料定义

图5 工作台滑块约束、施力与测量图

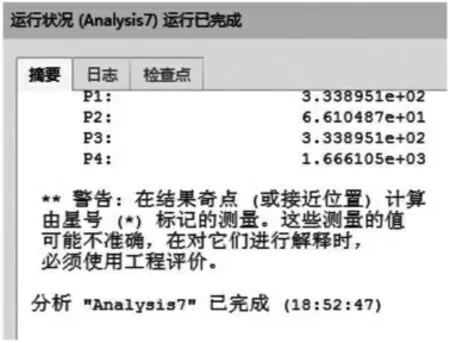
图6 分析结果信息

其余按照Creo5.0 有限元分析流程进行分析即可。分析后查询结果如图6所示。

P1=333.9 N，P2=66.1 N，P3=333.9 N，P4=1666.1 N。

2.2 Creo5.0分析结果说明

Creo5.0 分析结果与按载荷计算公式（7）～式（10）计算所得略有差异。本文中例1所给数据分析结果的绝对误差约为0.5 N，相对误差不足1%，完全满足工程需要。这种差异由两方面导致：一是有限元分析方法所致。众所周知，有限元分析实质就是将连续系统通过网格划分转变为离散系统。“离散就意味着精度丧失，也可以说每一种离散都体现了某种程度的精度”[7]。二是Creo5.0软件程序设计所致。

从Creo5.0对例1中数据的分析结果来看，正好验证了本文推导的载荷计算公式（11）～式（14）及式（7）～式（10）是正确的。

3 结语

通过本文的推导与Creo5.0有限元分析，笔者认为，目前文献[1]～[6]本质上所给出图1中的滑块载荷计算公式是错误的，其正确解可按文中公式（11）～式（14）或式（7）～式（10）计算求得，不过比较而言，式（11）～式（14）简捷许多。只要受力模型与图1中一致，文中式（11）～式（14）或式（7）～式（10）即可利用。其为夹具、机械手、自动化等设备设计制造中载荷的计算提供了正确的理论依据。