球轴承CSALT加速载荷边界值估算方法改进研究
沙美妤,王洪新,林华,曹昌勇,周小超
(皖西学院机械与车辆工程学院,安徽六安237000)
0 引言
球轴承属于长寿命产品[1],对其寿命及可靠性研究多基于加速寿命试验。恒加寿命试验(Constant Stress Accelerated Life Testing,CSALT)是最早发展起来的一种加速试验方法[2]。进行CSALT的前提之一是不同加速载荷(即加速应力)下的失效机理不发生改变,而这由前期试验设计和试验后期的一致性检验保证,其中试验设计环节主要通过确定合理的加速载荷边界值来保证失效机理的一致性。在设计CSALT方案时,试验的最大加速载荷越大,加速效果越好,试验时间越短,试验成本越低,在相同时间内得到的可用寿命信息越多[3]。但若其值过大,就会导致失效机理改变,使试验失去意义。以往人们主要根据经验来确定加速载荷边界值,再利用Hertz接触理论验证所选边界值的最大接触应力是否小于轴承最大允许接触应力,若小于则初步认为设计轴承的失效机理不发生改变,反之失效机理改变。该方法受设计人员实践经验的限制,估算结果往往与实际值有较大偏差,而且该试算法不便于工程应用。
本文以6206型轴承为例,利用Hertz接触理论估算球轴承最大接触应力的逆过程,推导出球轴承允许的理论疲劳极限载荷估算公式,并结合有限元分析结果对其进行修正,得到一个更为安全且便于工程应用的球轴承CSALT加速载荷边界估算公式。
1 基于Hertz接触理论的理论疲劳极限载荷估算公式
1.1 Hertz接触理论
Hertz接触理论是基于3个基本原理[4]提出的,具体如下:1)变形方程。点接触物体受力变形后,接触面呈椭圆形,而且相触物体的变形是连续的。2)物理方程。接触物体的变形在弹性阶段以内,广义胡克定律(Hooke)对其变形适用,接触面内应力与应变的关系成线性,且最大应变接触区域的中心应力最大。3)静力学平衡方程。根据接触表面压应力分布规律求得表面接触压力所组成的合力应等于外加载荷。而Hertz点接触进一步假设[5]:相触面积极小;相触面光滑忽略摩擦;相触面呈椭圆形;忽略介质的影响;相触物体只发生弹性变形,各向同性。
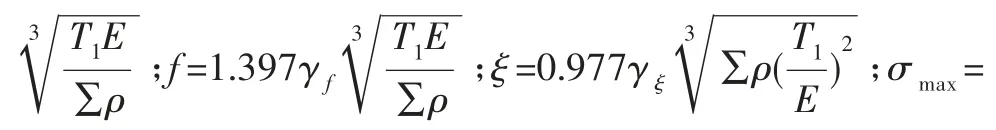
1.2 深沟球轴承的受载分析
本文研究的深沟球轴承在实际工作时受载十分复杂,此处为了便于分析,对其做如下简化:1)忽略轴向载荷,只考虑径向载荷的影响;2)忽略径向游隙的影响;3)不考虑受力变形造成的压线偏角。
简化后力学模型 如 图1 所 示,由STRIBECK理论[7]可知最下面滚球承受的载荷最大,其承载力与轴承径向载荷之间的关系为T1=Fr/n。式中:Fr表示轴承承受的径向载荷;n表示滚球个数。

图1 6206型深沟球轴承受力示意图
1.3 推导理论疲劳极限载荷的估算公式
根据上述公式,利用Hertz接触理论估算最大接触应力的逆过程,推导出外加径向载荷Fr的估算公式为

将轴承材料的最大允许接触应力σrnmax作为临界代入上式,得到理论疲劳极限载荷Frnmax的估算公式为
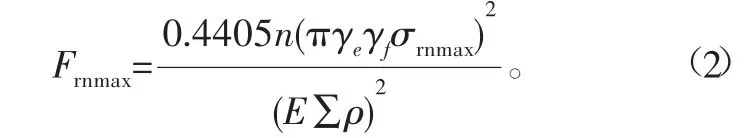
2 理论疲劳极限载荷值与ANSYS分析结果的对比
2.1 研究轴承的相关参数
本文研究的6206型轴承,其内外圈和滚球材料均是GCr15钢,且经过850 ℃淬火、160 ℃回火2 h,弹性模量为E=207 GPa,泊松比均为0.3,轴承钢的最大允许接触应力为4200 MPa。工作状态是内圈旋转、外圈固定,其它参数如表1、表2所示。

表1 研究轴承的相关参数
2.2 理论疲劳极限载荷值
若将理论疲劳极限载荷Frnmax直接作为理论加速载荷边界Smax的值,则Smax估算公式为Smax=Frnmax。根据表2及式(2)可估算出研究轴承的理论疲劳极限载荷值,即理论加速载荷边界值,相关估算结果如表3所示。

表2 研究轴承的最大接触应力相关理论计算值
2.3 基于ANSYS 的有限元分析值
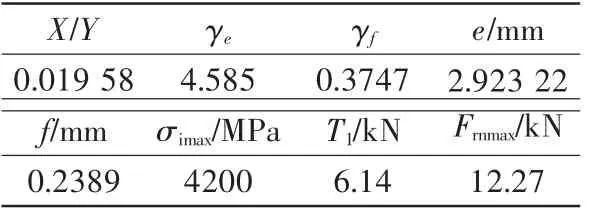
表3 研究轴承的理论疲劳极限载荷估算结果
根据Frnmax=12.27 kN及上述研究轴承的相关参数,将轴承自重、摩擦力等影响因素考虑进去,利用ANSYS Workbench软件进行接触分析,分析结果如图2和表4所示。
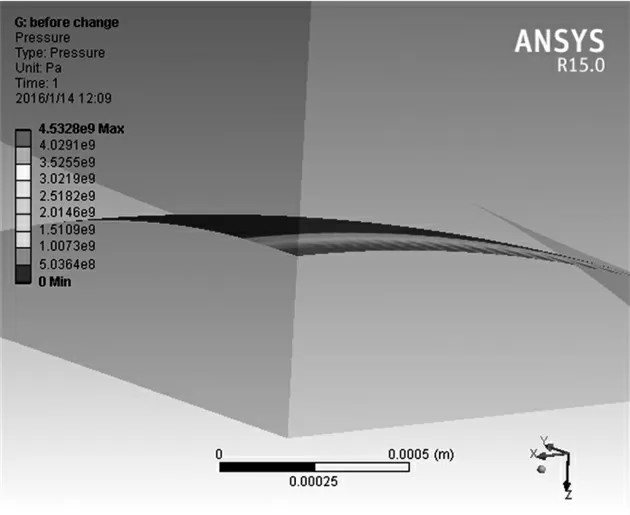
图2 研究轴承在载荷Frnmax下的最大接触应力云图
由表4可知,当外加载荷为Frnmax时,ANSYS 分 析 出的最大接触应力为4532 MPa,比σrnmax=4200 MPa高出7.9%。这是由于理论疲劳极限载荷估算公式忽略了自身重力、摩擦力等因素,而有限元分析考虑了这些因素。在有些工程应用中,10%左右的偏差在允许范围以内,但是在球轴承CSALT中,若将Frnmax作为最大加速载荷,其实际接触应力会超出允许值,会出现失效机理改变、试验数据失效等情况,无法保证球轴承CSALT的基本前提——失效机理不发生改变,这显然是球轴承加速寿命试验所不允许的。因此,不能将理论疲劳极限载荷Frnmax直接作为加速载荷的上限,必须予以修正。

表4 研究轴承的有限元分析结果
3 修正加速载荷上限估算公式
利用ANSYS求解出5.00、7.00、9.00、11.00、12.27 kN下研究轴承的最大接触应力,并拟合出基于有限元分析的加速载荷边界与最大允许接触应力关系曲线,分析结果如表5所示,拟合曲线如图3所示。

表5 不同径向载荷下最大接触应力的有限元解
当最大允许接触应力为4200 MPa时对应的有限元加速载荷边界值为9.81 kN,是理论加速载荷上限值12.27 kN的79.95%,比理论值小了20.05%,这进一步证明不能将理论疲劳极限载荷Frnmax直接作为加速载荷的上限。考虑到有限元分析结果与实际也会有一些偏差,再结合球轴承CSALT的实际情况,本文取理论疲劳极限载荷Frnmax的75%作为球轴承CSALT加速载荷边界值,则修正后加速载荷边界值的估算公式为

图3 基于有限元分析结果的拟合曲线
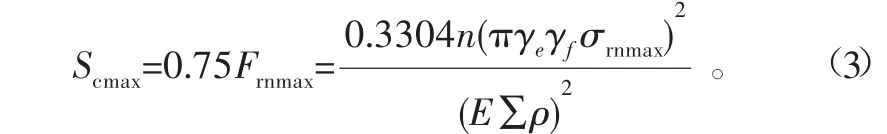
如图4所示,曲线A为轴承修正后理论曲线,曲线B为轴承修正前理论曲线,曲线C为基于有限元拟合的曲线,直线D表示最大允许接触应力为4200 MPa。由图4可知,当最大允许接触应力相同时,曲线B对应的理论加速载荷边界值最大,基于有限元分析拟合的曲线C对应的数值比理论值小10%左右,曲线A对应的加速载荷边界值最小,与拟合值的偏差在5%以内,曲线A更为保守安全。

图4 研究轴承修正前后对比图
4 试验验证
试验对象为检验合格的SKF6205型轴承样件,总样本数为3;试验设备为加速寿命试验机ABLT-1A;试验状态为内圈旋转、外圈固定;试验转速为6000 r/min;润滑油采用ISO VG 32;环境温度不超过50 ℃。根据修正的加速载荷边界估算公式,确定加速载荷边界值为7.7 kN;停机阈值均方根值大于20。试样失效后,对其进行失效机理的一致性检验,3个试验样本扫描电镜结果如图5所示,可明显看出剥落面为鱼鳞状断面,这是疲劳失效的典型特征,样件的失效机理没有发生改变。

图5 4个加速载荷下失效样件微观图
5 结语
本文基于Hertz接触理论及有限元法估算最大接触应力的优缺点,利用Hertz接触理论估算球轴承最大接触应力的逆过程,推导出轴承允许的理论疲劳极限载荷估算公式,并结合有限元分析结果对其进行修正,得到球轴承CSALT加速载荷边界估算公式,并经试验验证该估算公式更为安全可靠,可以在前期试验设计时较好地保证试验失效机理的一致性,达到较好的加速效果,更加满足加速寿命试验方案的设计要求。

