利用凯恩方程对气源辅助式六自由度运动模拟平台进行动力学建模
刘国军
(湖南理工学院 机械学院,湖南 岳阳414006)
0 引言
由于具有承载能力高、精度高等优点,采用Gough-Stewart平台结构的六自由度运动模拟平台被广泛用作多种运动模拟平台[1]。在自行武器动态模拟试验台中,六自由度运动模拟平台被用来复现自行武器系统行进时的运行姿态,为在实验室内测试自行武器火控系统的性能提供实验条件。传统的重载六自由度运动模拟平台常采用液压运动系统,但液压运动系统易污染、易泄漏、维护较复杂[2]。但随着大功率直流电动机和矢量控制技术的发展,电动运动系统开始逐步替代液压运动系统,它具有作动器走位精确、噪声低、无污染、预防性及修正性的维护大大减小等特点[3-4]。
为了满足重载情况需要,需通过增加额外驱动的方法来提高电动六自由度运动模拟平台系统的负载能力,如:采用6+3总共9个电动缸驱动整个六自由度运动模拟平台的冗余驱动并联机器人[5];也可以增加3个气缸来平衡负载和动平台的重力,从而减小电动缸驱动电动机的耗能,作为全球领先的六自由度运动平台系统的设计者和制造者,穆格公司的炮塔测试系统采用6个主动电动缸加3个被动气动缸驱动的六自由度运动模拟平台(即为气源辅助式六自由度运动模拟平台),最大动载荷可达到235.2 kN[6]。
国内外很多学者对六自由度运动模拟平台的建模进行了研究,但对气源辅助式六自由度运动模拟平台研究的文献很少。李晓成等[2]对气源辅助式六自由度运动模拟平台进行了优化,在对气源辅助式六自由度运动模拟平台进行动力学建模时,没有详细的过程,只是简化模型。为了以后能对气源辅助式六自由度运动模拟平台进一步进行优化设计、响应特性等深入研究,需要建立它精确的动力学模型。为了便于使用计算机[7-9],本文将采用凯恩方程来建立气源辅助式六自由度运动模拟平台的动力学反解模型。
1 系统描述
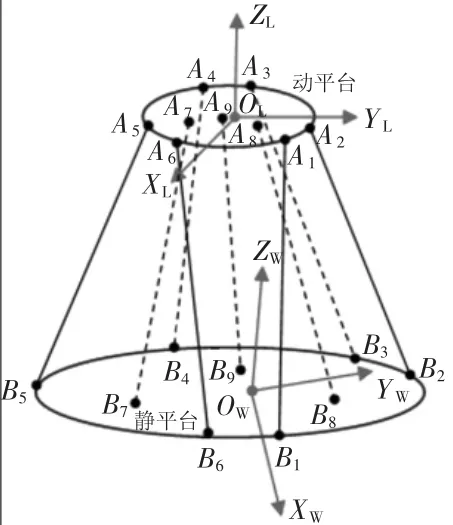
图1 气源辅助式六自由度运动模拟平台示意图
气源辅助式六自由度运动模拟平台如图1所示,Ai(i=1,2,3,4,5,6)为电动缸连接于动平台上的铰点中心,Bi(i=1,2,3,4,5,6)为电动缸连接于静平台上的虎克铰中心。Ai(i=7,8,9)为气缸连接于动平台上的虎克铰中心,Bi(i=7,8,9)为气缸连接于静平台上的虎克铰中心。为了适用一般情况,把控制点OL设置为与铰圆圆心不重合的点。在动平台上建立体坐标系{L}——坐标系原点为OL的直角坐标系OL-XLYLZL。在静平台上建立惯性坐标系{W}——坐标系原点为OW的直角坐标系OW-XWYWZW。
6个上铰点Ai(i=1,2,3,4,5,6)和6个下铰点Bi(i=1,2,3,4,5,6)连线分别为对称六边形(3条长边和长边分别对应相等)。3个气缸的上铰点Ai(i=7,8,9)和下铰点Bi(i=7,8,9)连线也分别为等边三角形。9个上铰点Ai在同一个平面上。9个下铰点Bi也在同一个平面上,如图2所示。上铰圆圆心为O1,半径长rA,如图2(a)所示。下铰圆圆心为点O,半径长rB,如图2(b)所示。以O1和O为原点,分别建立坐标系{L1}与{W1}。坐标系{L1}(即O1-X1Y1Z1)即为把OL-XLYLZL平移到原点O1。坐标系{W1}(即OXYZ)即为把OW-XWYWZW平移到原点O。Z1轴垂直于上铰面,X1轴为A6与A1连线的中线。上铰点和下铰点六边形的短边长度分别用dA和dB表示。气缸在动平台上的3个铰点在同一个圆上,并构成一个等边三角形,圆的半径记为rPA,如图2(a)所示。Z轴垂直于下铰平面,X轴为B6与B1连线的中线。气缸在静平台上的3个铰点在同一个圆上,并构成一个等边三角形,圆的半径记为rPB,如图2(b)所示。
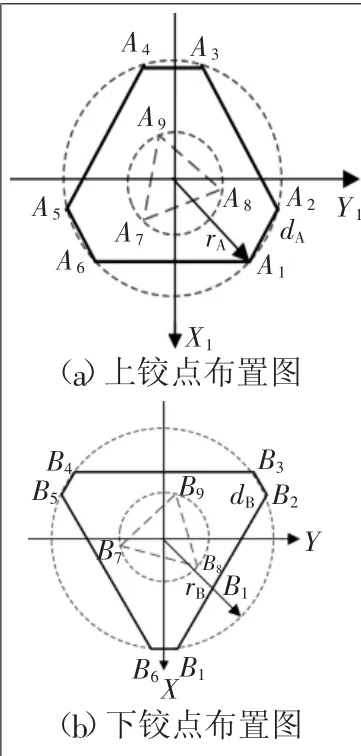
图2 铰点位置示意图
Lw和w1分别表示点O1在坐标系{L}和点O在坐标系{W}中的位置。规定:当矢量在惯性坐标系{W}中表示时不用标注;在其它坐标系中时,需要用左上标标注坐标系;用方括号“[]”加下标“×”表示两个矢量叉乘,即有a×b= a×[]b。
根据前面的定义有:

其中:



2 位置、速度和加速度反解
已知动平台的位姿,求解9个支路中电动缸(或液压缸)与气缸移动的长度、速度及加速度,分别称为位置、速度和加速度反解[10]。
为了分析的方便,建立了第i个支路坐标示意图(如图3)。图中:点C1i表示第i个支路中缸筒端的质心;点C2i表示第i个支路中活塞杆端的质心;点m1i表示第i个支路中缸筒端的质量;点m2i表示第i个支路中活塞杆端的质量;t表示矢量OOL;bi表示矢量OWBi;pi表示矢量OLAi;矢量BiAi用lini表示,其中li表示矢量BiAi的长度,ni表示矢量BiAi的方向;c表示动平台与负载的综合质心C到原点OL的矢量OLC;矢量OWC用rc表示;WRL表示坐标系{L}到{W}的旋转矩阵,后面的依此类推;以点Bi为原点建立体坐标系{L1i}——右手直角坐标系Bi-XiYiZi,其中:Zi沿ni方向;Yi沿ni×z^(其中z^表示坐标系{W}中Z轴的单位矢量方向)方向。把坐标系{L1i}移动到以Ai点为原点建立坐标系{L2i}——Ai-XiYiZi。c1i、c2i分别表示上缸筒端质心和活塞杆端质心分别在{L1i}和{L2i}中的位置矢量,且是在坐标系{W}中表示的。

图3 第i个支路坐标示意图
2.1 位置分析
根据Ai的位置矢量关系得到

式中:
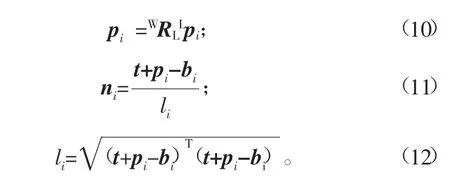
根据旋转矩阵的方向余弦表示方法,可得到旋转矩阵WRL1i为
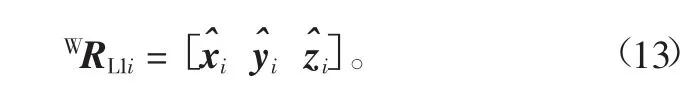
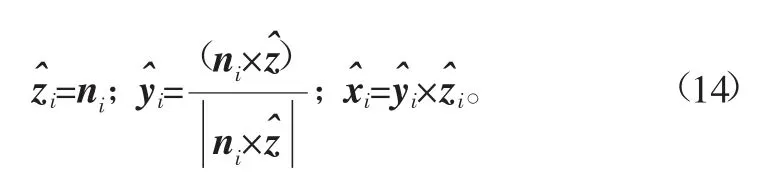
缸筒端和活塞杆端质心在坐标系{W}中的位置矢量r1i、r2i分别为:
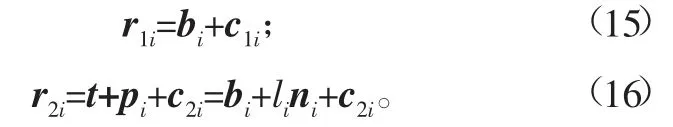
根据矢量关系可得到综合质心C的位置矢量为

2.2 速度反解
把液压缸、电动缸和气缸的支路都当作UPS(U表示虎克铰、P表示移动副、S表示球铰)结构来分析。
式(9)右边对时间求导,得到上铰点Ai在坐标系{W}中的平动速度vAi为

式中:vAi表示上铰点Ai在坐标系{W}中的平动速度;vP=t·表示动平台上控制点OL在坐标系{W}中的平动速度;t·表示t对时间求导;ωP表示动平台在坐标系{W}中的转动角速度。
式(9)左边对时间求导,也可得到上铰点Ai在坐标系{W}中的平动速度vAi,为

式中:ωi表示支路i在坐标系{W}中的转动角速度;l·i表示支路i的伸缩速度大小。
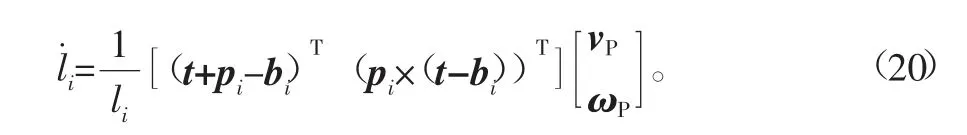
忽略液压缸(电动缸)和气缸绕自身轴线转动的影响,即假设

式(19)两边左叉乘ni,可得到ωi为

分别对式(15)和式(16)求导,得到:

式中:v1i表示缸筒端质心的平移速度;v2i表示活塞杆端质心平移速度。
式(17)对时间求导,可得到综合质心C的速度为
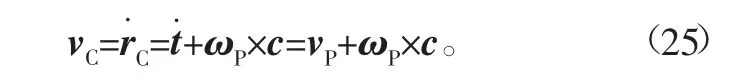
式中,vC表示综合质心C在坐标系{W}中的平动速度。
把9个支路的伸缩速度大小与动平台上控制点的速度关系合成为一个矩阵,有
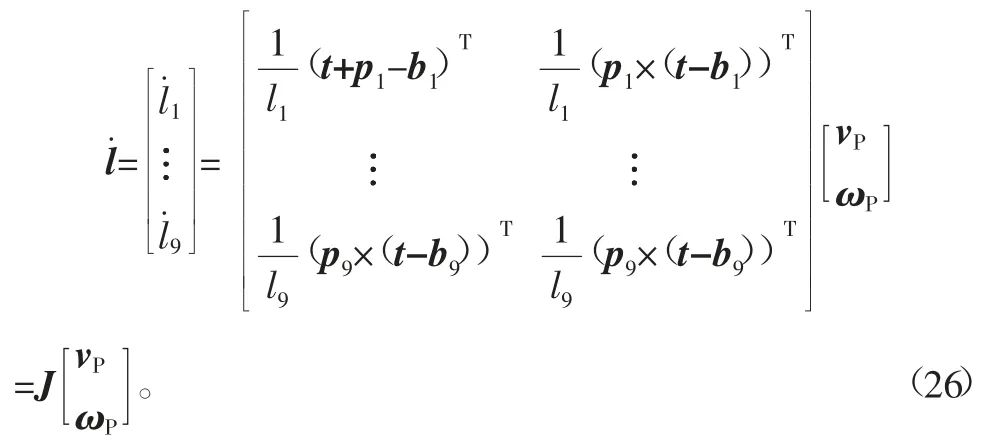
式中雅可比矩阵J为

2.3 加速度反解
式(26)对时间求导得到各个支路的伸缩加速度大小为
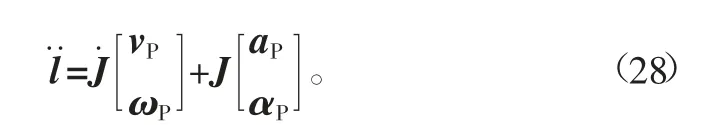
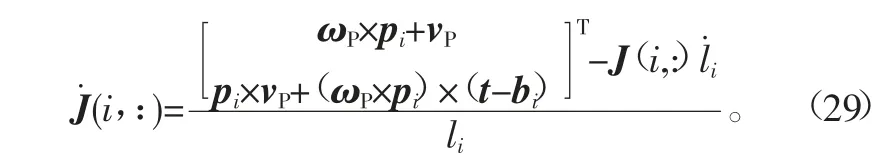
分别对式(23)和式(24)求导,得到:
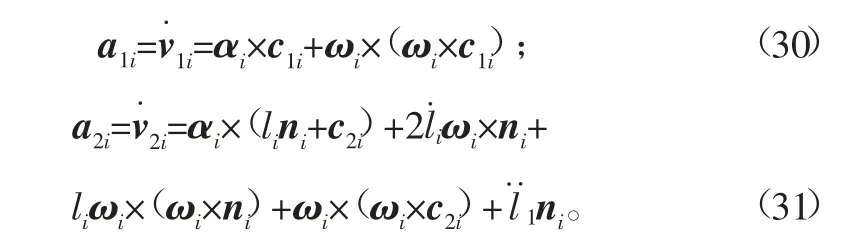
式(25)对时间求导,可得到综合质心C的加速度为
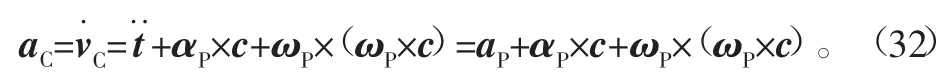
式(22)对时间求导,可得到支路i在坐标系{W}中的转动角加速度为
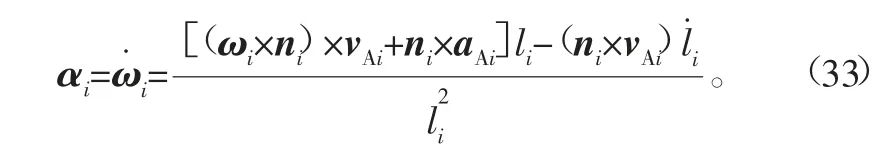
式(19)左边对时间求导,也可得到上铰点Ai在坐标系{W}中的平动加速度为
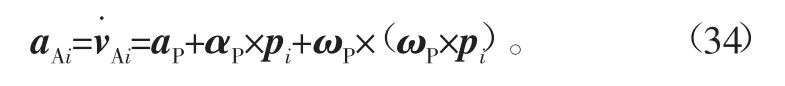
3 动力学建模
3.1 雅可比矩阵
为了得到紧凑的解,要建立各个力作用点、惯性力(或力矩)作用点等的速度与动平台上控制点速度之间的雅可比矩阵。
由式(18)得到
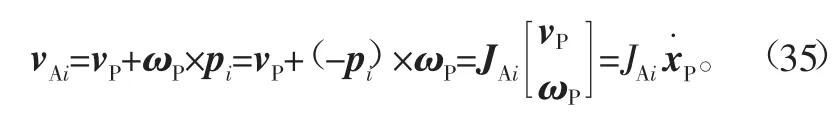
式中:
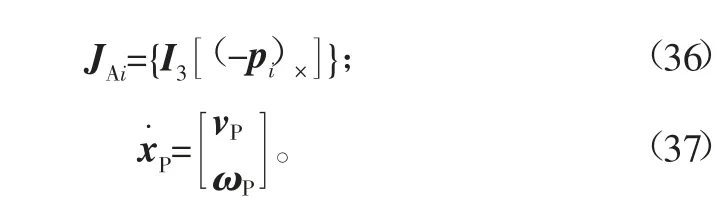
其中,I3表示3×3的单位矩阵。
由式(22)和式(35)得到
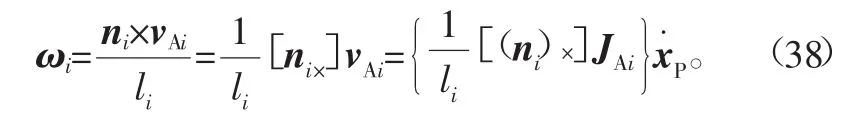
由式(23)和式(38)得到

由式(24)、式(26)和式(38)得到

把式(38)~式(40)结合起来得
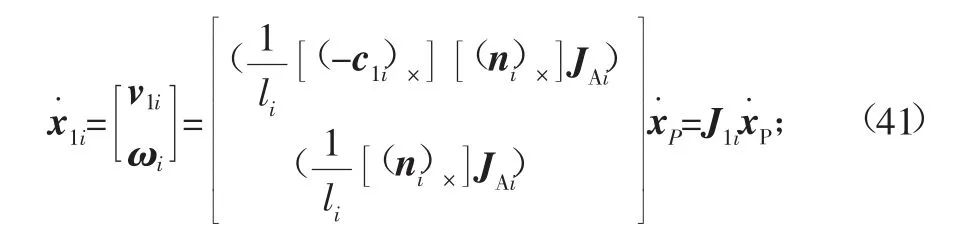
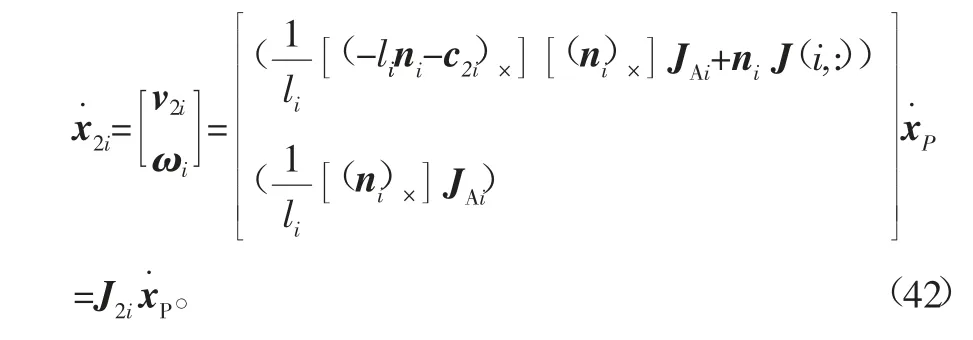
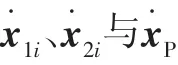
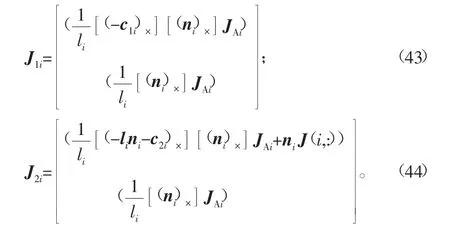
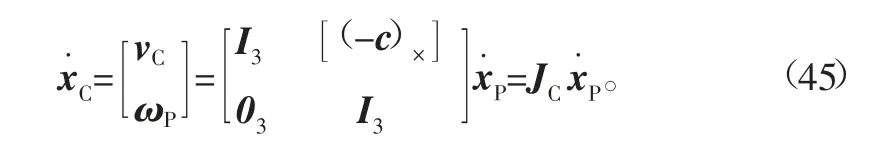
雅可比矩阵JC为

3.2 利用凯恩方程建立动力学反解模型
凯恩方程的表达式如下[11]:


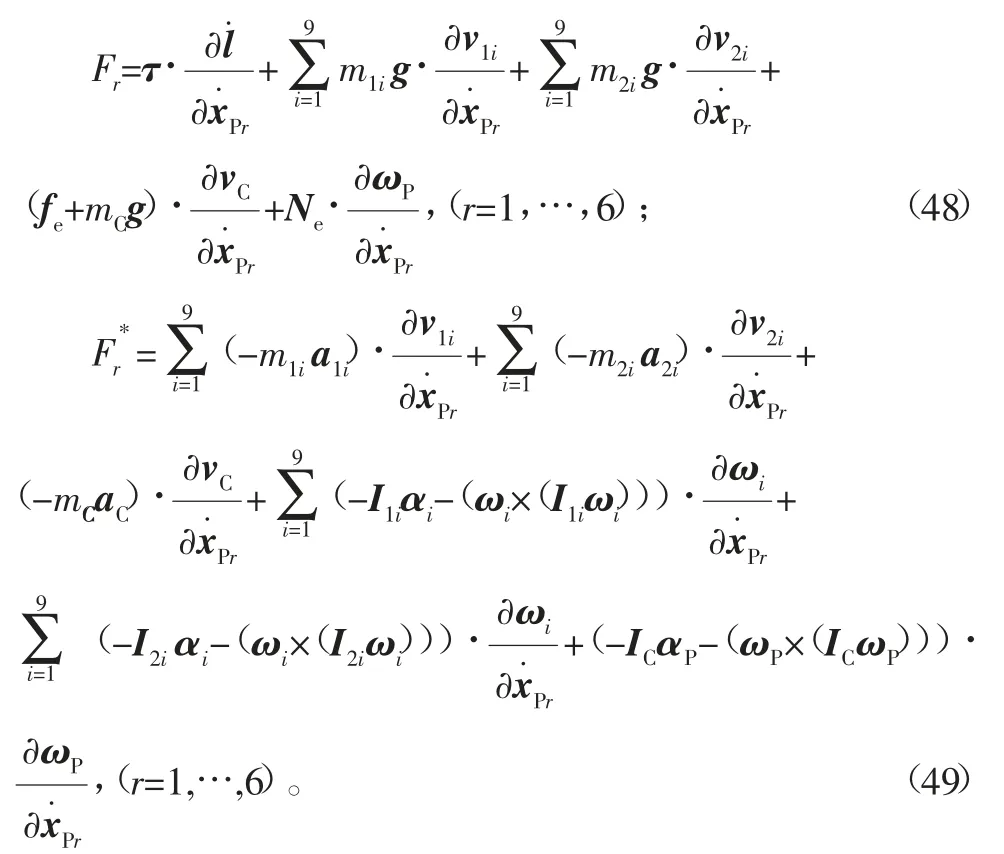
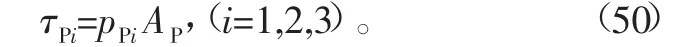
气缸中驱动力大小是由活塞的作用面积和气缸中气体压力的乘积,即为:式中:pPi表示第i个气缸中气体压力的大小;AP表示气缸中活塞的作用面积大小。
在恒温过程中,封闭容器内气体的压力和容积的乘积为一个常值,即有[12]

式中:p为封闭容器内气体的压力大小;V为封闭容器内气体的容积大小。
假设对于每个气缸都单独配备一个储气罐,则有

式中:p0表示动平台在中位时,给储气罐加的初始压力大小;V0表示储气罐的容积大小;l0i表示动平台在中位时,第i个气缸缸筒端活塞杆端面到气缸缸筒底面的距离;l1i表示在当前位姿时,第i个气缸缸筒端活塞杆端面到气缸缸筒底面的距离。
由式(52)得到

又假设对于3个气缸一起配备一个储气罐,则有
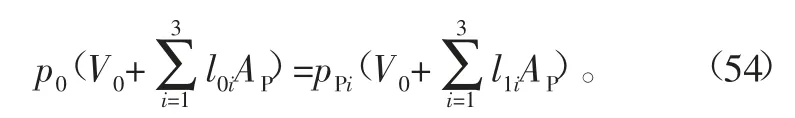
由式(54)得到
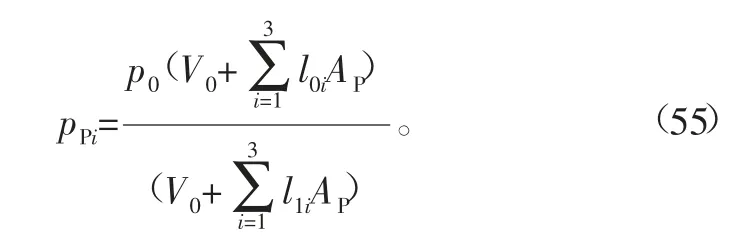
在运动模拟平台运动过程中,气缸的出力τPi是已知力。把6个广义主动力和广义惯性力分别合成为一个列向量,然后把式(26)、式(41)、式(42)和式(45)分别代入式(48)和式(49)中得到:

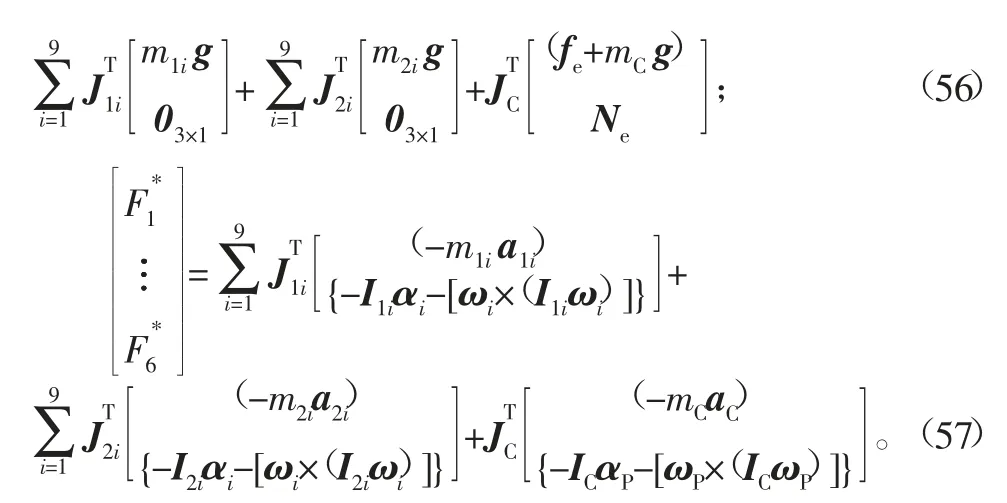
式中,03×1表示元素全为0的3维列向量。
由式(56)、式(57)和式(47)得到:

式中,06×1表示元素全为0的6维列向量。
当雅克比矩阵J(1:6,:)可逆时,由式(58)两边左乘(J(1:6,:)T)-1,得到6个电动缸的驱动力大小为

式中F为

当设计的初始阶段,并不知道电动缸和气缸的质量与惯量矩阵的值。且对于重载六自由度运动模拟平台,由于负载太大,电动缸和气缸的质量、重力与惯量矩阵对计算它们的驱动力大小影响较小,在初始阶段时,可忽略不计。即此时得到6个电动缸的驱动力大小为

式中F′为
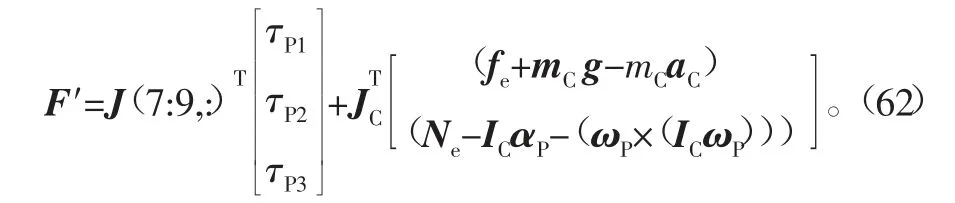
4 结论
本文考虑气缸中气体压力的变化,分别对3个气缸一起配备一个储气罐和各个气缸单独配备一个储气罐中气缸出力进行了推导,然后利用凯恩方程对气源辅助式六自由度运动模拟平台建立了动力学模型,为进一步对气源辅助式六自由度运动模拟平台的优化和控制性能仿真等研究提供了详细的动力学模型理论基础。

