含未知输入的离散线性系统新型递归滤波方法
花玉,王娜,b,赵克友
(青岛大学 a. 自动化学院;b. 山东省工业控制技术重点实验室, 山东 青岛 266071)
0 引言
当系统存在过程噪声和测量噪声的情况下,传统卡尔曼滤波器[1]能递归估计线性系统状态,但是其要求干扰噪声必须是高斯白噪声。因为系统的不确定干扰可能不是白噪声,且某些输入无法测量,因此卡尔曼滤波器的效果有时并不理想。
在系统分析中,未知输入可以表示无法测量的干扰、未建模动态、系统故障等。因此,研究含有未知输入的系统估计问题具有极大意义。这类问题的解决方案在控制系统设计中的干扰抑制[2-3]、故障检测[4]、电池状态估计[5]等许多实际应用中发挥重要作用。
近年来,存在未知输入的滤波器设计问题引起了相当大的关注。根据系统不同,该问题可大致分为两类:带有直通项的滤波器设计[6-12]和不带直通项的滤波器设计[13-17],其中关于不带直通项的滤波器设计文献相对较少,具有进一步研究的价值。
最初,解决这类问题的方法是系统状态扩维,将未知输入向量作为系统状态的附加部分,然后对扩维系统应用卡尔曼滤波器。这种方法通常将未知输入假定为常值偏差或某些具有已知统计特性的随机过程[18],但这些假设在实际应用中可能是无效的。因此,许多研究开始转向存在任意未知输入情况下的系统状态估计问题。解决此类问题的方法通常是通过解耦来实现状态估计。
自从KITANIDIS P K开展工作以来,对未知输入估计问题的研究开始转向最优滤波器,其为不带直通项的线性系统,开发了一种最小方差无偏(minimum variance unbiased, MVU)的最优滤波器[13]。该滤波器通过在无偏条件的约束下将状态协方差矩阵的迹最小化以获得状态估计。该滤波器被文献[14]进一步扩展为一类参数化解决方案。上述文献虽然解决了存在未知输入时的状态估计问题,但没有给出未知输入的估计值。对一些实际问题来说,未知输入的估计值同样重要。文献[16]提出一种鲁棒两段卡尔曼滤波器(robust two-stage kalman filter,RTSKF),首先识别初始时刻未知输入的动态模型,然后用识别的模型对未知输入和状态进行估计,其能够给出未知输入的具体估计值,但没有证明所得结果最优。文献[17]提出一种三步迭代滤波器(recursive three-step filter, RTSF),能够同时获得系统状态和未知输入的最小方差无偏估计,并证明了未知输入估计值最优。尽管上述滤波器可以解决存在未知输入下系统状态及未知输入的估计问题,但都有一个前提条件:系统状态方程中未知输入的系数矩阵列满秩。
本文基于RTSF思路,提出一种新型三步迭代滤波器(novel recursive three-step filter,NRTSF),在系统状态方程受未知输入影响时估计系统状态和未知输入,该滤波器不需要系统方程中未知输入系数矩阵列满秩,其应用条件比上述滤波器宽松。
1 问题描述
考虑如下带有未知输入的随机线性离散时变系统:
xk=Ak-1xk-1+Gk-1dk-1+wk-1
(1)
yk=Ckxk+vk
(2)


2 NRTSF设计
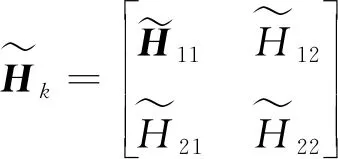
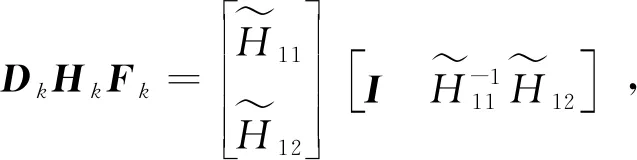
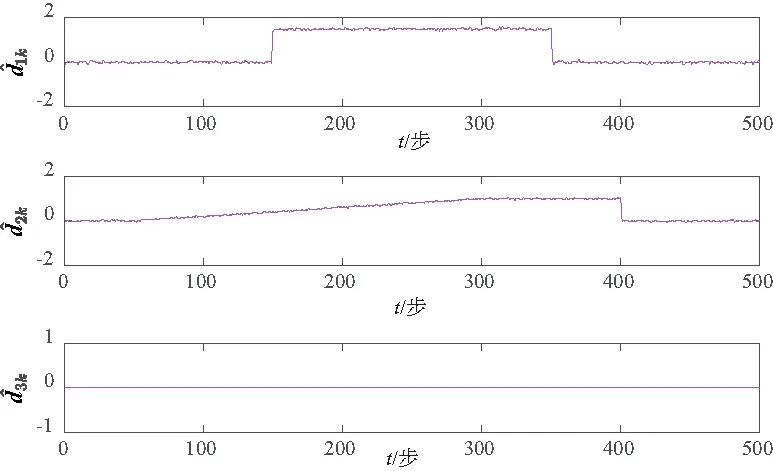
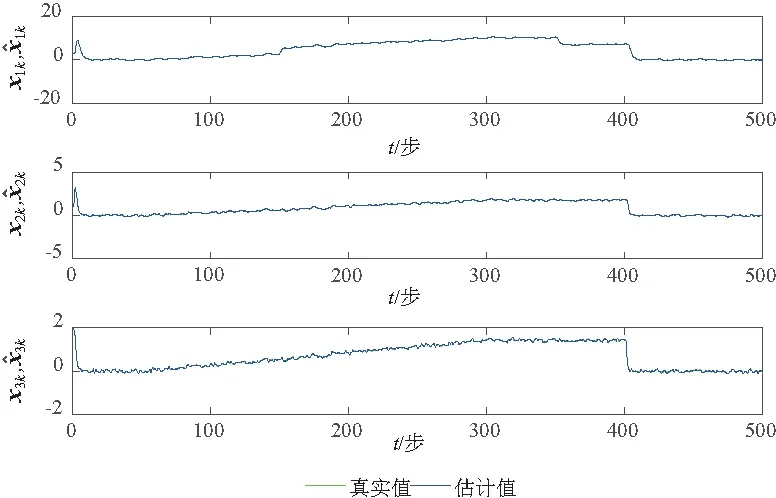
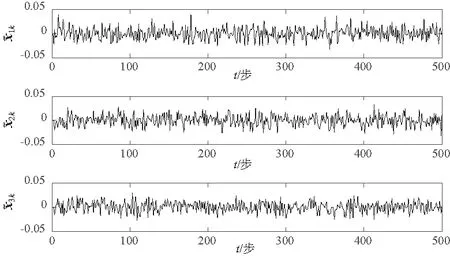
GILLIJNS S在文献[17]中提出的经典RTSF可以解决上述系统的状态估计问题,但是使用RTSF的前提条件是系统方程中未知输入的系数矩阵Gk-1必须满足rank(Gk-1)=m,k=1,2,…。针对系统方程中未知输入系数矩阵不满秩的情况,即rank(Gk-1)=rk 假如rank(Gk-1)=rk≤m,对其进行如下满秩矩阵分解: (3) 换言之,存在非奇异阵Dk∈Rp×p和Fk∈Rm×m,使 (4) 则原系统方程式(1)改写为 (5) 基于新的系统状态方程式(5)和测量方程式(2)设计NRTSF如下: (6) (7) (8) 1)虚拟未知输入的无偏估计 (9) 其中 (10) 证明: 该证明与文献[17]中定理1的证明相似,因此省略。 由于对应于式(9)的最小二乘解满足定理1,因此这个最小二乘解无偏。但根据Gauss-Markov定理,它不一定是最小方差解,因为在一般情况下 其中c表示正实数。 2)虚拟未知输入的MVU估计 证明: 该证明与文献[17]中定理2的证明相似,因此省略。 (11) (12) (13) (14) 证明:使用拉格朗日乘子法来证明此定理。令拉格朗日式 (15) (16) 式(16)和式(12)组成线性系统方程组 (17) 将式(14)代入式(8)产生等效状态更新: 将式(14)代入式(13)可得 将NRTSF总结如下: 1)时间更新 2)虚拟未知输入估计 3)测量更新 为了验证本文提出的NRTSF有效性,本节采用与杜涛[19]一致的示例进行仿真。 假设线性系统的相关矩阵如下: 图1 未知输入dk的实际值 图2是应用NRTSF得到的未知输入估计结果图。从中可以看出NRTSF能够估计未知输入d1k、d2k,但是对未知输入d3k没有估计效果,造成这一现象的原因是系数矩阵GK不满秩。因此未知输入d3k没有影响到系统状态,进而导致量测值中没有未知输入d3k的信息。 图2 未知输入dk的估计值 图3和图4分别是应用NRTSF得到的系统状态的估计结果图和系统状态估计误差结果图,由于未知输入分别加在前3个系统状态分量,所以图中分别给出了前3个系统状态x1k、x2k和x3k的真实值、估计值以及估计误差,由图3和图4可以看出状态估计值都能够跟踪状态真实值。 图3 系统状态及其估计值 图4 系统状态估计误差 本文针对系统方程含有未知输入的情况,讨论了同时估计未知输入和状态的问题,针对经典滤波器的不足,提出一种新的三步迭代滤波器,其可以解决系统方程中未知输入系数矩阵不满秩时,经典滤波器无法使用的问题。仿真结果表明,新滤波器能够有效估计未知输入及系统状态。
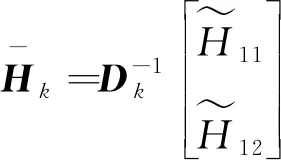
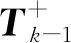


2.1 时间更新



2.2 虚拟未知输入估计
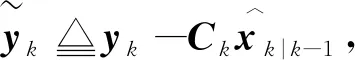

2.3 测量更新




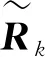
2.4 NRTSF迭代步骤总结
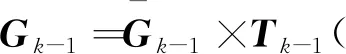
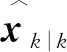
3 仿真结果分析


4 结语

