基于离子运动和离子扩散效应的电解电容建模
薛田良,曾阳阳,张赟宁,2,陈 曦
(1.三峡大学 电气与新能源学院,湖北 宜昌 443000;2.三峡大学 智慧能源技术湖北省工程研究者中心,湖北 宜昌 443000)
0 引言
电容器是电子电路中不可缺少的基本元件,占电子元件总消耗量的40%,广泛应用于人类生活的各个方面[1]。然而,在电力电子设备中电容器存在最高的故障率[2]。因此,对电解电容器的状态进行监测和建模具有重要意义,对元件的使用寿命、维护成本以及相关应用的安全性具有深远的意义。
等效串联电阻(ESR)是监测电容器健康状态的一个重要研究方向。有学者发现随着电解电容器的劣化,电解电容器的ESR 增大[3]。当电容器的等效串联电阻增加到初始值的200%以上时[4],通常被认为是故障[5]。可以通过追踪ESR 来监测电容器的健康状态[6]。
在常用的电解电容器建模中,使用传统的整数阶微积分不足以准确描述这类元器件的电气特性[7]。同时,文献[7]也指出电解电容器具有分数阶特性,可以考虑引入分数阶对系统建模。相比使用整数阶对电解电容器建模,考虑采用分数阶导数对分析电容器提供了一条可行的思路,一方面,分数阶系统可以减少系数来表示复杂的非线性现象的系统;另一方面,分数阶的任意阶数提供了更高的自由度[8]。
随着人们对分数阶微积分的认识,有学者将恒相位的电容应用到电解电容的建模中,取得了较好的结果。研究发现分数阶电容可以替代传统的整数阶元件[9]。文献[10]发现,具有恒定相位角单元的分数阶微分模型的精度与五阶RC 模型相似,有力地证明了锂离子电池分数阶微分模型的性能优越。文献[11]设计了一种分数阶参数估计方法,扩大了更新阶的选择范围,使算法的收敛性更加平滑,分数阶在这个方面优于整数阶。
随着分数阶的发展,电解电容器模型逐步得到了改进,但是仍存在一些不足。H.Malek 等学者提出了一种基于分数阶元件的电容等效电路模型[12]。陈曦在此基础上,对模型进行了改进,在模型中增加了一个分数阶元件的电解电容器,提高了监测精度[13]。然而,随着电化学领域的发展,电解电容器电解液中发生的一些化学现象还没有被考虑到建模之中。例如文献[14]发现在电池中有一种特殊的离子扩散现象。受此启发,本文对电解电容器的模型进行改进。
本文首先考虑了电解电容器的内部工作原理,分析了电解电容器的失效原因。然后,在现有的电解电容模型的基础上,引入分数阶建模,考虑离子的运动和扩散,提出了一种新的电容模型。本文同时对ESR 和阻抗Z进行跟踪,以识别电解电容器的健康状况。然后利用差分进化算法(DE)对模型参数进行辨识。最后,通过仿真验证了该方法的有效性。
1 电容器建模
1.1 常用电容器模型
现有的电解电容器模型一般采用简单的RC 串联和并联,如图1 所示。在工业上,这些模型已被制造商Vishay 和Nichicon 广泛使用[15]。在学术领域,这些模型被用于电子电路直流滤波器、电容状态监测、整流电容滤波器等控制方向[12,16]。研究发现,电容器的阻抗Z和ESR 随温度和频率的变化而变化[17⁃18]。根据电路串并联原理,由电解电容器的等效串联电路等效出电容器的阻抗Z和ESR,观察它们随频率的变化。然而,图1a)所示的等效模型在宽频率范围内,不能准确估计ESR,当频率高于10 kHz 时,误差较大[19]。随着研究推进,图1b)、图1c)和图1d)逐渐被提出[12⁃13]。

图1 各种电容器模型
模型图1b)中Ct是电容的标称值,Rd和Cd的并联部分等效为电解液的介电损耗。R0,R1分别代表电容器端子和箔片的电阻,其阻抗Z为:

已知,ESR 为阻抗的实部,则由式(1)可得:

在FO1 模型中,考虑了电容器电极表面的自相似分形结构,引入阶次α对电容器进行修正,得到阻抗和ESR 分别为:

对FO2 模型而言,其等效串联电容器模型的阻抗Z,ESR 分别为:
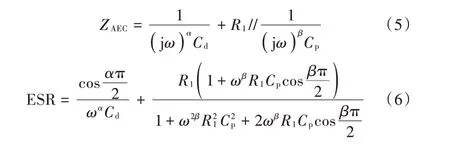
以上模型就是常用的电解电容器模型及其阻抗Z和ESR。
1.2 基于离子运动和离子扩散的分数阶模型
电解电容器都有一定的使用寿命,受多种因素的影响,包括过电压、高温、尖峰充放电等,进而导致阻抗Z的变化[20]。电解电容器在工作过程中,内部发生的一些化学现象更是不能忽略的。
当电容器在高温下工作时,电容器电解液中的水分子分解成离子。离子运动导致电极根部发生电化学腐蚀。同时,离子迁移与电极的氧化还原反应导致漏电流增大,甚至导致短路和电极被击穿。因此,离子运动对电解电容器的健康监测具有重要作用。当电容器通电时,离子的扩散使电解液中的一些阴离子黏附在粗糙的电极表面,一些在电解液中解离,形成两层结构。
有趣的是电池和电解电容器的结构有许多相似之处。电解电容器和电池的等效模型是电容器与电阻的串并联。此外,文献[19]发现电池中的扩散现象引入电解电容器中是可行的,并且很大一部分电解液电阻被转移到异常扩散部分[21]。电池的扩散现象是指离子会在电池的多孔电极表面转移[14]。电容器在生产中,阳极板腐蚀严重,有效面积增大。在电解电容器内部,既具备带有离子导体的电解质,又具备类似于多孔电极的高度腐蚀的阳极板。因此,可以假设电容器电极表面的刻蚀等效于电池板的孔隙率,并将电池中的扩散现象引入到电解电容器的建模中。

图2 基于离子运动和离子扩散的新模型
基于以上发现,本文主要考虑了离子的运动和扩散现象,并在频域内监测了电容器的健康状况。在电解电容器建模过程中,对传统的功率电容模型图1a)进行了改进,将离子运动和离子扩散等效为电阻和普通电容的并联,如图2a)所示。此时相应的阻抗Z和ESR 如下:

引入分数阶修正模型以反映复杂的扩散现象。将离子运动和离子扩散等效为电阻和α阶电容的并联,其中,α为非整数。提出的分数阶电容模型如图2b)所示。根据串并联电路的简化原理,可以得到下列方程:

后文将对常用的等效模型(FOe 模型、FO1 模型、FO2 模型)和提出的等效模型(IO⁃HOT 模型、FO⁃HOT 模型)进行参数辨识和仿真,以验证模型的有效性。
2 参数拟合
第1 节已经完成对模型元件和组成的确定,接下来还需要确立模型参数。因此将模型参数的确立转化为一个优化问题。为了识别等效模型的各个参数,利用ESR 和Z构造目标函数。将ESR 与Z的拟合问题转化为多目标优化问题来识别参数向量,从而使目标参数最小化,即寻求最小值。与文献[13]一样,将ESR 和Z与实测数据的均方差作为目标函数,如下:
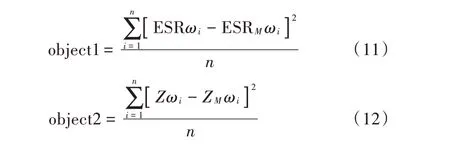
式中:ESRωi是等效串联电阻预测值;ESRM ωi是等效串联电阻实测值;Zωi是阻抗的预测值;ZM ωi是阻抗实测值。
具体采用的是一种启发式优化算法——差分进化(DE)算法。DE 算法主要包括变异、交叉和选择部分,可以用于参数拟合中的多目标拟合问题[13]。具体的算法原理如下:
1)设置种群规模、变异比例因子、交叉操作概率等基本参数。
2)初始化种群并获取每个种群中每个个体的适应度。
3)从种群中随机选择最大值和最小值作为变异源,并利用比例因子将这两个值的差异向量与种群中的其他个体相结合,生成新的变异个体。
4)在目标个体和突变个体之间进行二项式交叉运算,产生实验个体。
5)计算并比较实验个体和目标个体的适应度值。按适应值大小选择当前适应值。如果测试个体的适应度值优于目标个体,则测试个体将在下一代中替换目标个体;否则,目标个体将继续存在。
6)DE 算法通过迭代计算保留适应度好的个体,剔除坏的个体,并引导搜索过程求解全局最优解,最终输出最优结果。
3 仿真及结果
为了验证所提出模型和算法的有效性,考虑使用标称值为10 μF 的50 V rubycon PX 系列电容器进行实测。通过Wayne Kerr WK65120 精密阻抗分析仪在25 ℃、(100 Hz,100 kHz)频带内实测电容器的ESR 和阻抗Z,其ESR 和阻抗Z变化见图3 和图4 中的实测曲线。

图3 基于DE 算法的电容器模型参数辨识结果

图4 等效模型实测值与预测值的ESR 比较
对于参数辨识部分,根据不同的模型、种群大小设定为待识别参数维数的20 倍,最大迭代次数设置为200,比例因子为0.85,交叉概率为0.8,突变因子为0.35。选择DE/rand⁃to⁃best/1 突变策略[22]和二项分布的交叉策略。
采用DE 算法对各个模型的参数进行辨识,结果见图3,共识别出5 个模型,其中,除IO⁃HOT 模型外,其余4个模型均为分数阶模型。图3 清楚地显示了要确定的参数数量和每个模型的已识别参数的值。由图3 可知,模型越复杂,需要识别的参数就越多。
参数拟合后,在Matlab 中进行了仿真,得到了ESR等效电路模型和阻抗Z的预测数据。模型的ESR 和Z监测结果如图4 和图5 所示。由于电解电容器的工作频率通常小于100 kHz,因此在100 Hz~100 kHz 范围内进行预测。

图5 等效模型测量值与预测值阻抗Z 的比较
ESR 和Z不仅取决于温度,而且还取决于工作频率。测量值也很好地反映了ESR 和Z随频率的变化。由图4 和图5 可以看出,仿真结果呈现出ESR 和Z的变化趋势,这些模型能够很好地描述了电解电容器的ESR和阻抗Z随工作频率的增加而降低的过程。当频率从100 Hz 增 加 到100 kHz 时,ESR 从4.17136 Ω 下 降 到1.04254 Ω,Z由169.065 Ω 下降到0.973804 Ω。通过比较各模型监测ESR 和Z的绝对误差值,可以得到模型监测误差随频率的变化趋势,如图6 和图7 所示。

图6 等效模型ESR 预测误差值的比较

图7 等效模型阻抗Z 预测误差值的比较
根据误差图分析5 个模型的ESR 在100~1000 Hz频率范围内有明显的上升或下降趋势,其中,整数阶IO⁃HOT模型的ESR和阻抗Z变化都最为剧烈。在1~10 kHz范围内,4 种分数阶模型的ESR 误差在0.2 Ω 以内,并逐渐减小,最终趋于平稳;在10~100 kHz 范围内,4 种分数阶模型和整数阶模型的电阻监测误差约为0 Ω。由图7 可以看出,在整个频率范围内,除了IO⁃HOT 模型,其他模型的拟合效果都很理想。由此可见,引入分数阶后对模型的修正作用,分数阶监测模型FO⁃HOT 比IO⁃HOT 模型在阻抗Z的监测中具有更高的精度,其中,拟合效果最好的是FOe 模型,其次是FO⁃HOT 模型、FO2 模型、FO1 模型、IO⁃HOT 模型。FO⁃HOT 模型虽然对阻抗Z不是最佳拟合,但是其精度相对其他模型仍占优势。
4 结 论
本文提出一种新的电解电容器模型,通过跟踪ESR和阻抗Z来监测电解电容的健康状态。仿真结果表明了差分进化算法的有效性,进一步验证了提出的分数阶模型的优越性。与其他分数阶电解电容器模型相比,本文模型虽然辨识参数有所增加,但误差明显减小,对铝电解电容器的监测更为准确。

