Interplay of parallel electric field and trapped electrons in kappa-Maxwellian auroral plasma for EMEC instability
M Nazeer,M N S Qureshi and C Shen
1 Department of Physics,GC University,Lahore(54000),Pakistan
2 Shenzhen Graduate School,HIT Campus,University Town of Shenzhen,Shenzhen 518055,China
Abstract In this paper,propagation characteristics of electromagnetic electron cyclotron(EMEC)waves based on kappa-Maxwellian distribution have been investigated to invoke the interplay of the electric field parallel to the Earth’s magnetic field and auroral trapped electrons.The dispersion relation for EMEC waves in kappa-Maxwellian distributed plasma has been derived using the contribution of the parallel electric field and trapped electron speed.Numerical results show that the presence of the electric field has a stimulating effect on growth rate,which is more pronounced at low values of wave number.It is also observed that as the threshold value of trapped electron speed is surpassed,it dominates the effect of the parallel electric field and EMEC instability is enhanced significantly.The electric field acts as another source of free energy,and growth can be obtained even in the absence of trapped electron drift speed and for very small values of temperature anisotropy.Thus the present study reveals the interplay of the parallel electric field and trapped electron speed on the excitation of EMEC waves in the auroral region.
Keywords:EMEC waves,kappa-Maxwellian distribution,trapped electrons,parallel electric field in aurora
1.Introduction
An electric field associated with magnetospheric wave phenomena was first suggested by Alfven and Falthammar[1]on the basis of theoretical arguments,and has been an important feature of auroral plasma over the past couple of decades.Numerous observations from magnetospheric plasma reveal that such an electric field predominantly occurs along the Earth’s magnetic field[2–6].Auroral observations by the Viking satellite have shown that the time duration of electric fields are a few tens of seconds and their values are from a few to 20 mV m−1[7].Based on the observations of the electric field associated with electrostatic shocks and double layers from the auroral zone,Temerin and Mozer[8]inferred that the average peak value of parallel electric fields is 25 mV m−1.However,observations from the auroral region also reveal that electric fields are found with amplitudes more than 100 mV m−1,but these electric fields are restricted to relatively small regions[9,10].Mozer and Kletzing[11]reported the direct observations of large amplitude electric fields of more than 100 mV m−1from the upward current auroral region.From the upward current auroral region,the direct observations of parallel electric fields pointed out the localization of these fields almost up to 10 Debye lengths[12].Furthermore,Schriver and Ashour-Abdulla[13]reported that large- and small-scale electric fields exist in the auroral region.Shi et al[14]studied the nonlinear electrostatic waves in the context of auroral plasma and suggested that bipolar electric field solitary structures could be the result of nonlinear evolution of such electrostatic waves.Therefore,the existence of an electric field parallel to the magnetic field in the auroral region has now been well established.

Figure 1.Normalized growth rate versus normalized wave number for different values ofEo=0,40 60,80 mV m−1 and v0/c=0 with other parameters ne/n=0.9,β=0.15,θ‖/c=θ⊥/c=0.1,ωpe/Ω e=0.8andκ=4.
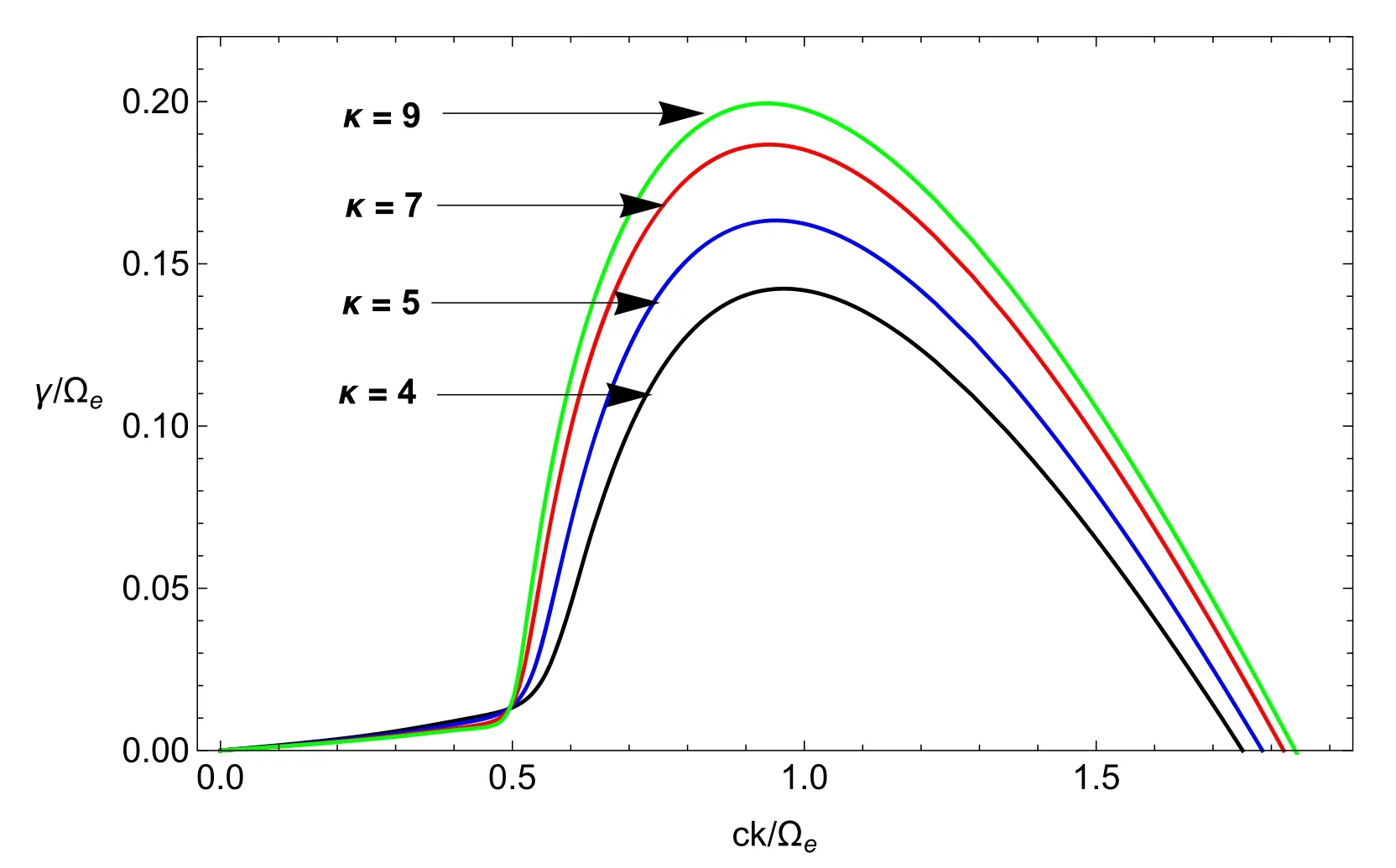
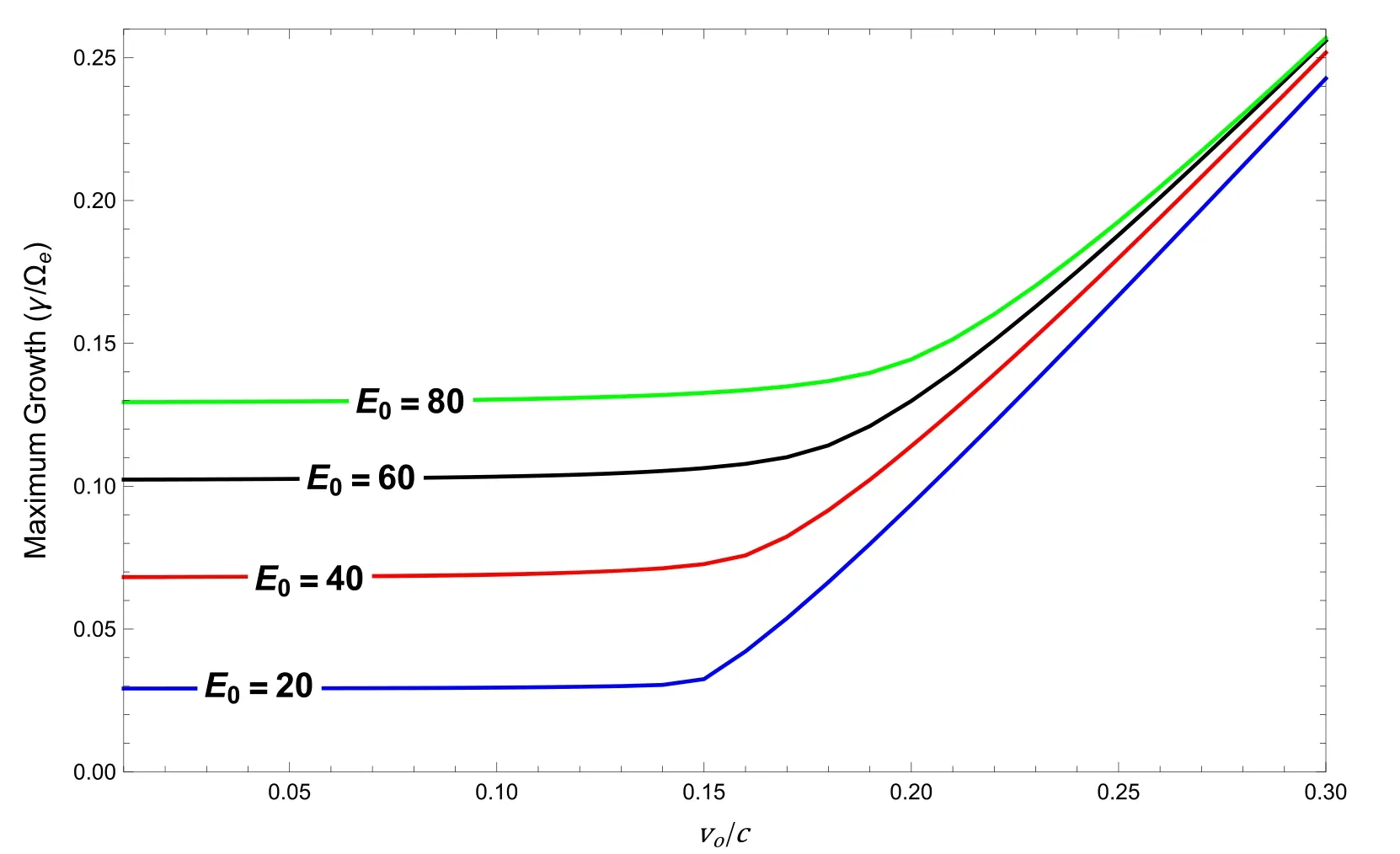
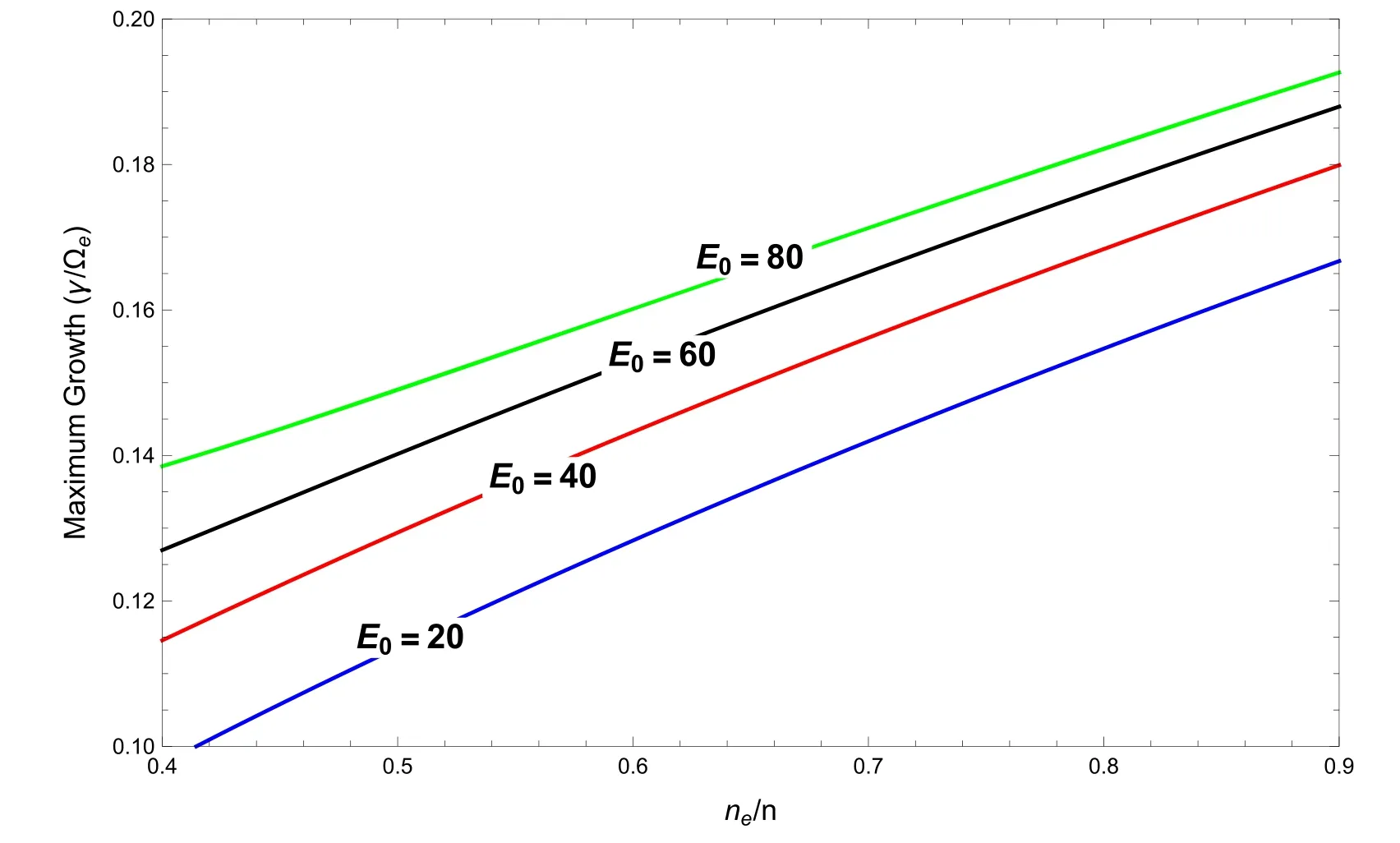
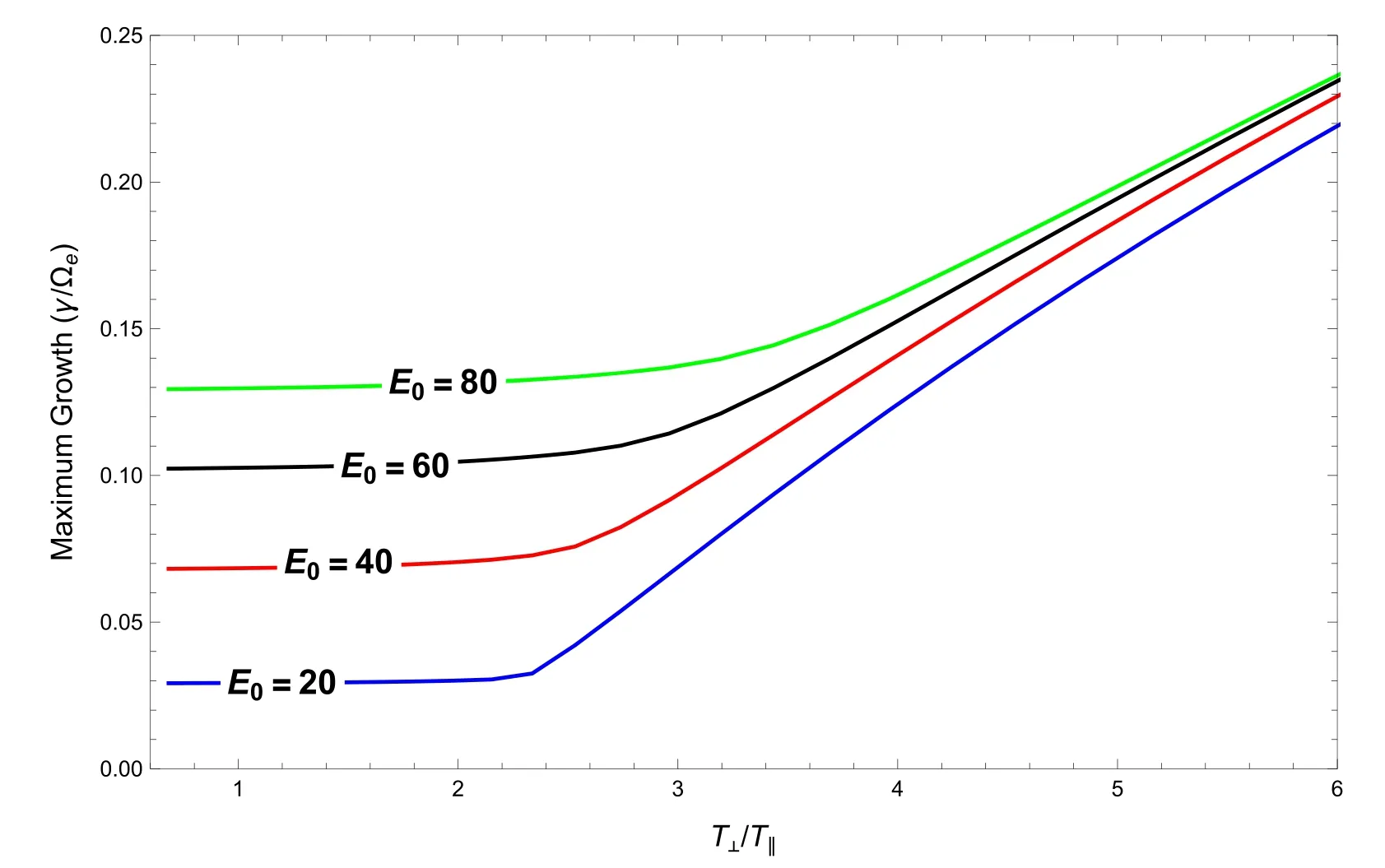
The presence of an electric field and electrodynamical coupling of the ionosphere and magnetosphere have a significant effect on the regional electrodynamics and transportation of charged particles.One of the commonly observed electromagnetic waves in the magnetosphere is electromagnetic electron cyclotron(EMEC)waves.The electron temperature anisotropy and streaming electrons are supposed to be the cause of excitation of these waves[15].Whistler waves are the low-frequency branch of the full spectrum of EMEC waves that have been observed extensively in terrestrial foreshock,magnetosheath and magnetosphere[16].The presence of the electric field may affect the morphological characteristics of whistler waves generated by the wave particle interaction.By employing the bi-Maxwellian distribution,Misra and Singh[17]found out how EMEC waves are amplified by electric fields in weakly ionized Maxwellian plasma,but this work was restricted to a small value of temperature anisotropy.In the auroral region,for large values of temperature anisotropies,Renuka and Viswanathan[18]investigated the EMEC instability in a plasma which consists of a nonthermal cold component and Maxwellian hot component.It is worth noting that we employ kappa-Maxwellian distribution function,whereas in[17,18]bi-Maxwellian was used.Excitation of whistler waves has also been studied in low-altitude auroral plasma,comprising cold and trapped energetic electrons withne In this paper,using linear kinetic theory,EMEC instability has been studied to explore the interplay of trapped electron speed and parallel electric field in the context ofκMdistributed auroral plasma.The growth rate for EMEC instability has been derived using theκM-distribution for arbitrary values of trapped electron density and various altitudes.A theoretical model and the derivation of dispersion relation for EMEC waves inκM-plasma are presented in section 2.In section 3,we present the numerical solution and effect on the growth rate studied by changing the different plasma parameters.Finally,we present our conclusions in section 4. In this paper,we assume uniform,collisionless and anisotropic plasma comprising cold ionospheric background electrons and trapped energetic(hot)electrons in the presence of a parallel electric field which is a salient feature of auroral plasma.These energetic trapped electrons exhibit a bump along the perpendicular axis in velocity space[20].Moreover,we consider ion population as immobile providing neutralizing background; therefore,ion dynamics is completely neglected.TheκM-distribution function is considered as a model distribution for trapped energetic electrons in whichκ-distribution is used to model the parallel accelerated motion and perpendicular motion is modeled by Maxwellian distribution.Thus the distribution function for trapped electrons is written as[39] where Hereneis the energetic electron andnis the total electron density,v0is the mean energetic trapped electrons drift speed in the perpendicular direction defined aswherewithErfc()is the complementary error function,and are the modified parallel and perpendicular electron temperatures,respectively.Here we note that the parallel thermal velocity shown in equation(3)is modified due to the presence of the parallel electric field,and has the form whereE0is the parallel electric field and(Nazeer et al 2018).Alternatively,is modified due to the presence of the parallel electric field[40,41],as given below Equations(5)and(6)represent the modified parallel thermal velocity and parallel temperature in the presence of the parallel electric field,respectively.For a system that comprises cold and trapped energetic electrons,the dispersion relation for EMEC waves propagating parallel to the ambient magnetic field forκM-distributed plasma can be written as are the modified plasma dispersion functions expressed through Gauss hypergeometric function corresponding to kappa andκM-distributions,respectively[25,32]with argumentIn the limiting form,i.e.κ→∞,both the modified dispersion functions reduce to plasma dispersion functionZ(ξ)[42]. After some manipulation,equation(7)can also be written as where WhenEo=0,the dispersion relation(8)can be reduced to equation(6)of Nazeer et al[39]Also whenEo=0andvo=0,the dispersion relation(8)reduces to equation(33)obtained by Cattaert et al[33]for theκM-plasma. The real frequency and growth rate can be obtained by solving the above dispersion relation(8)using the large argument of dispersion functions and taking only the lowest order terms havingEoin the imaginary part.We also assume that cold background electrons are isotropic and only cold electrons contribute to real frequency[20,27,39]; the expression of real frequency can be written as From the above equation,we can see that the real frequency is not only independent of the parallel electric field,but also independent of the energetic electrons[17,20,27,43].Therefore,in the following section we will not plot the real frequency and restrict our analysis to growth rate only.Since the energetic electrons are responsible for the growth,therefore,the growth rate can be calculated as WhenEo=0,the above expression reduces to the expression obtained by Nazeer et al[39]The expression given above reveals that the instability will be significant if the following conditions are fulfilled. The above conditions govern the upper and lower bounds for the instability,respectively.The above conditions also show that there is no influence ofκ-index on the threshold frequency while the maximum unstable frequency strongly depends uponκ-index[29]. Numerical solution of the complete dispersion relation(equation(8))for the EMEC waves is presented in this section by considering different values of the parametersEo,θ‖/c,v0/candne/ncfor auroral plasma[20,35,44].Figure 1 depicts the plots of growth rateγ/Ωeversus wave numberck/Ωefor different values ofEo=0,40 60,andv0/c=0 with other parametersne/n=0.9,β=0.15,θ‖/c=θ⊥/c=0.1,ωpe/Ωe=0.8andκ=4.We can note that the parallel electric field(Eo>0)has a stimulating effectv0/c=0.This is due to the fact that the parallel electric field on the growth rate,and growth can be obtained even for serves as another independent source of free energy and can accelerate the electrons along the magnetic field up to such energies that can excite the wave.Generally growth can be obtained whenv0/chas a value greater than the threshold value,since it enhances the resultant temperature anisotropy,which is the source of instability for EMEC waves.However,the present study reveals that growth can be obtained even whenv0/c=0 when there is some nonzero background electric field present in the system as an additional source of energy. In figure 2,growth rateγ/Ωeis plotted against the wave numberck/Ωefor different values ofEo=0(black),20(blue),40(red),80(orange)in mV m−1whenn n e=0.9,v0/c=0.25,ωpe/Ωe=0.8,κ=5,θ‖/c=θ⊥/c=0.1 andβ=0.2.In figure 2,enhancement of growth rate with the increase in the value of parallel electric field at low values of wave number is evident.We can also note that the range of wave number for which instability occurs also increases with increments in the value ofE.oFigure 3 is plotted for normalized growth rateγ/Ωeagainst the normalized wave numberck/Ωefor different values ofκ=4(black),5(blue),7(red),9(green)whenEo=10 mVm−1,ne/n=0.9,θ‖/c=θ⊥/c=0.1,v0/c=0.24,ωpe/Ωe=0.8andβ=0.1.We can see that there is an enhancement in the growth rate with the increase in the kappa value.We can also note that the range of wave number for which instability occurs also increases with the increase in the kappa. Figure 2.Normalized growth rate versus normalized wave number for different values of electric field Eo=0(black),20(blue),40(red), Figure 3.Normalized growth rate versus normalized wave number for different values of electric field κ =4(black),5(blue),7(red),9(green)whereωpe/Ωe=0.8,Eo=10 mV/m,ne/n=0.9,θ‖/c=θ⊥/c=0.1,v0/c =0.24 and β=0.1. The variation in maximum growth rateγ/Ωeagainst normalized plasma frequencyωpe/Ωehas been shown in figure 4 for different values ofEo=0,10,20,30,40 mV m−1andθ‖/c=θ⊥/c=0.1,ne/n=0.7,v0/c=0.2,,κ=2.In figure 4,it can be seen that when we increase the normalized plasma frequency for a fixed value ofEo,the maximu m growth rate increases initially,but after reaching a certain value growth becomes constant for further increase in the plasma frequency.Moreover,we can see that if we fix the(γ/Ωe)against the trapped electron drift speedv0/cfor varvalue of plasma frequency and increase the value of electric field,the growth rate also increases. Figure 5 shows the plots for maximum growth rate ious values ofEo=20,40 60,80 mV m−1and for fixed values ofn n e=0.9,β=0.1,ωpe/Ωe=0.8,κ=5 andθ‖/c=θ⊥/c=0.1.It can be seen that the effect of parallel electric field on the maximum growth rate is more pronounced at the smaller values of trapped electron speed.When we increase the drift speed,maximum growth remains constant initially but it remains higher for larger values of electric field for a fixed value of drift speed.We can also note that there is almost no effect of drift speed on the maximum growth until it reaches a certain threshold value.After reaching that threshold value,trapped electron drift speed dominates the instability and the effect of electric field on the instability reduces,but maximum growth rate increases at a much faster rate with the increase in the drift speed beyond the threshold. Figure 4.Normalized growth rate versus normalized plasma frequencyωpe/Ωefor various values of Eo=0,10,20,30,40 mV m−1 with other parameters ne/n=0.7,v0/c =0.2,θ‖/c=θ⊥/c=0.1,ωpe/Ωe=0.8andκ=2. Figure 5.Maximum growth rate versus normalized trapped electron speed for various values of Eo=0,40 60,80 mV m−1 and n ne/=0.9,β=0.1,ωpe/Ωe=0.8,θ‖/c=θ⊥/c=0.1,κ=5. Figure 6 illustrates the variation in maximum growth rate(γ/Ωe)versus normalized energetic trapped electron density for different values ofEo=20,40 60,80 mV m−1,while the other parameters areκ=4,ωpe/Ωe=0.8,β=0.1,v0/c=0.25,θ‖/c=θ⊥/c=0.1.From figure 6,it can be noted that the maximum growth rate increases with theincrease in energetic trapped electron density,but remains higher for larger values of electric field for the fixed value of trapped electron density.Figure 7 is plotted for maximum growth rate(γ/Ωe)versus temperature anisotropyfor different values ofEo=20,40 60,80 mV m−1with fixed parametersne/n=0.9,κ=4,β=0.1,θ‖/c=θ⊥/c=0.1,ωpe/Ωe=0.8.From figure 7,we can note that when we increase temperature anisotropy,maximum growth remains constant initially but is kept higher for larger values of electric field.We can also note that there is almost no effect of trapped electron drift speed on the maximum growth until it reaches a certain threshold value,which is more pronounced for smaller values of electric field.After reaching that threshold value,temperature anisotropy dominates the instability and the effect of electric field on the instability reduces.Furthermore,it is also noted that beyond thethreshold when we increase the temperature anisotropy the maximum growth rate increases significantly. Figure 6.Maximum growth rate versus normalized energetic trapped electron density for different values of Eo=20,40 60,80 mV m−1 and β=0.1,v0/c =0.25,ωpe/Ω e=0.8,κ=4,θ‖/c=θ⊥/c=0.1. Figure 7.Maximum growth rate versus temperature anisotropy for different values ofEo=20,40 60,80 mV m−1 with n ne/=0.9,θ‖/c=θ⊥/c=0.1,ωpe/Ω e=0.8,β=0.1 andκ=4. Figure 8.Maximum growth rate versusθ⊥/cfor different values ofEo=20,40,60,80 mV m−1 with ne/n=0.9,θ‖/c=0.1,β=0.1,v0/c =0.25,ωpe/Ωe=0.8andκ=4. Figure 8 gives the variation in maximum growth rate(γ/Ωe)versus perpendicular thermal velocity for various values ofEo=20,40 60,80 mV m−1with other parametersn e/n=0.9,θ‖/c=0.1,β=0.1,v0/c=0.25,ωpe/Ωe=0.8 andκ=4.The curves given in figure 8 reveal that when we increase the perpendicular thermal velocity,the maximum growth rate increases monotonically; however,if we fix the value of perpendicular thermal velocity,growth rate shows higher values for a larger electric field. In this paper,the influence of parallel electric field and trapped electron speed and their interplay have been investigated by employing kappa-Maxwellian distribution for auroral trapped electrons on the propagation characteristics of EMEC waves.The general dispersion relation in terms of modified dispersion functionZκM(ξ)bearing the effects of parallel electric field and trapped electron speed has been derived for the first time by employing kappa-Maxwellian distribution function.The analytical expressions for real frequency and growth rate are then derived and the full dispersion relation is investigated numerically.It is well known that in a drifting plasma the EMEC wave only grows when electron drift speed has values larger than a certain threshold value[39].However,in the present case our numerical results show that the EMEC wave grows well before the drift speed reaches a threshold value,and has a significant growth rate even for smaller values of parallel electric field.After the drift speed surpasses the threshold value,it dominates the EMEC instability and there is a significant increase in the growth rate.It is concluded that the parallel electric field has a stimulating effect on the growth rate at smaller values of wave number.It is also found that the presence of the electric field provides another source for free energy,and growth can be obtained even in the absence of trapped electron speed and for very small values of temperature anisotropy.In the present study the values of plasma-βand the ratioωpe/Ωehave been chosen so that they correspond to a wide range of auroral altitude(Fennell et al 1981).Moreover,with the increase in plasma frequency and perpendicular thermal velocity,the growth rate also increases,but it remains higher for larger values of electric field for the same values of plasma frequency and perpendicular thermal velocity.Thus the present study reveals the interplay of parallel electric field and trapped electron speed on the excitation of EMEC waves in the auroral region. This research was supported by the GC University grant No.241/ORIC/19 dated 27-08-2019 and National Natural Science Foundation of China Grant No.41874190.2.Model formulism


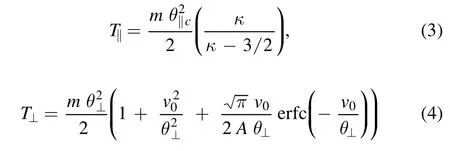




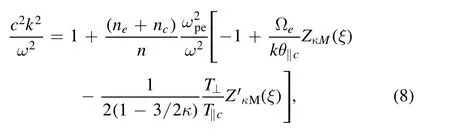
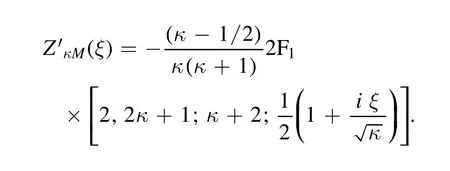
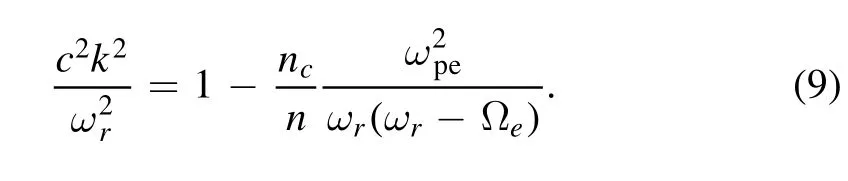

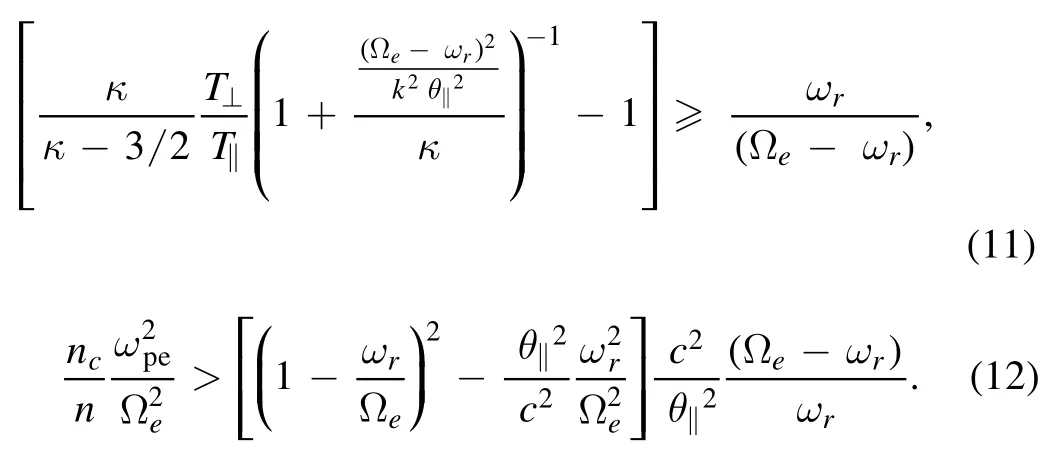
3.Numerical results



4.Summary and conclusion
Acknowledgments
 Communications in Theoretical Physics2021年1期
Communications in Theoretical Physics2021年1期
- Communications in Theoretical Physics的其它文章
- Edge effect and interface confinement modulated strain distribution and interface adhesion energy in graphene/Si system
- Effects of an anisotropic parabolic potential and Coulomb’s impurity potential on the energy characteristics of asymmetrical semi-exponential CsI quantum wells
- Effects of rebinding rate and asymmetry in unbinding rate on cargo transport by multiple kinesin motors
- Phase transitions of two spin-1/2 Baxter–Wu layers coupled with Ising-type interactions
- Three-dimensional cytoplasmic calcium propagation with boundaries
- Hidden periodicity in Stripe 82 with Saraswati supercluster—a fractal analysis
