气象探空火箭测风不确定度评估方法
孙宇 陈书驰 邵胜利 蔡俊武 何亿强 王芳栋 史荟燕
(1 北京航天飞行控制中心,北京 100094; 2 中国人民解放军32021部队,北京 100094)
引言
临近空间气象火箭探空测风模式为探空仪与火箭在上升段分离后,继续惯性运动到顶点,在下落过程中,降落伞逐渐张开,达到稳定状态后,在探空仪牵引下下落并随风飘移,降落伞成为高空风场的示踪物。根据探空仪记录的位置变化,可以反演得到临近空间20~60 km大气风场[1-7]。由此可知,相比于激光雷达或无线电雷达等遥感探测设备,火箭探空仪测风属于原位测量,其精度较高,对于工程应用和比对试验具有重要意义[8-9]。
气象火箭测风资料处理与常规气球探空不同。在50~60 km高度,由于空气密度很低,对降落伞—探空仪系统的拖洩力较小,根据降落伞位置信息算出的水平运动速度并不等于该高度空气块的水平移动速度,因此要对降落伞—探空仪系统的水平运动速度进行修正,从而得到该高度空气块的水平运动速度(即该高度上的水平风速)。由于风速修正公式中要用到降落伞—探空仪系统的移动速度和加速度,因此如何从所测的降落伞空间位置坐标计算获得这些速度和加速度?其误差是多少,以及因此导致风场反演结果的不确定度如何评估?这就是本文主要研究的问题。
1 风场反演数学模型
根据牛顿第二定律且忽略浮力和科氏力的影响,将降落伞—探空仪系统作为1个质点,建立平衡方程如下:
(1)

将式(1)改写为三维分量表达式:
(2)
式中,ax、ay、az为降落伞-探空仪系统运动加速度的三维分量;vx、vy、vz为降落伞-探空仪系统运动速度的三维分量;Vx、Vy为风速的南北、东西分量;Vz为垂直气流速度;gx、gy、gz为重力加速度的三维分量。
由于重力加速度在X、Y方向上的分量很小,故忽略gx、gy,令gz=g;通常情况下垂直气流速度Vz远小于降落伞-探空仪系统的落速,即vz-Vz≈vz。于是式(2)可简化为:
(3)
式(3)即为世界气象组织推荐的风速修正公式。
风向G可由下式表达(具体方向由Vx、Vy的正负号确定):
(4)
2 风场反演不确定度
根据误差理论[10],若间接测量量y=f(x1、x2、…、xn),则系统误差Δy有如下近似表达式:
(5)

随机误差是用表征其取值分散程度的标准差来评定的,对于函数y的随机误差,可用函数的标准差来评定。若各测量值的随机误差相互独立,则随机误差σy表达式如下:
(6)
式中,σx1,σx2,…,σxn为各变量的随机误差。
误差合成采用方和根合成法,则测量结果的总标准差Δ总为:

(7)
风场反演不确定度评估采用A类评定法,其标准不确定度uc等同于由一系列观测值获得的标准差Δ总,即u=Δ总,测量结果不确定度Y表达式为:
Y=y±uc
(8)
2.1 风速误差
根据误差理论,由式(3),可得风速系统误差表达式如下:
(9)
由式(6),可得风速随机误差表达式如下:
(10)
随机误差与系统误差合成采用方和根法。风速误差在X、Y方向上的分量为:
(11)
由误差合成原理可得风速误差为:
(12)
2.2 风向误差
根据误差理论,由式(4),可得风向误差表达式为:
(13)
在实际数据处理时,由于速度和加速度分量是对离散位置拟合后获得的,因此速度和加速度分量系统误差和随机误差需由拟合过程得出。下面通过推导得到采用最小二乘法进行多项式拟合的风场系统误差和随机误差表达式。
3 最小二乘法多项式拟合的系统误差和随机误差
3.1 速度拟合的系统误差
设探空仪的在下落过程中的真实位置可以通过一个k次多项式给出:
x(t)=a0+a1t+a2t2+…+aktk
(14)



(15)
式中,Pk(i)为正交多项式的k次项;P′k(i)为关于Pk(i)中对i的一阶导数;Δt为数据点之间的时间间隔;N为用于拟合的数据点个数;k为拟合多项式次数。
根据正交多项式性质可得:
(16)

(17)
下面对最小二乘法进行1~4次多项式拟合的系统误差公式进行推导。
3.1.1 线性拟合
线性拟合条件下,拟合段中点的速度表达式为:
(18)
用式(14)代换为:
(19)
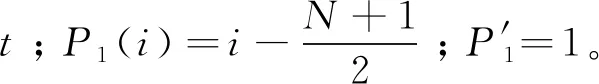

(20)
式(20)中大括号中的项可利用正交多项式的恒等式特点求解:
(21)
将式(21)代入式(20)可得:
(22)
由式(14),拟合段的中点速度可表示为:
(23)
因此,对于线性拟合而言,速度的系统误差(实际速度和拟合速度之间的差(式(22)-式(23))如下:
(24)
由于系数a0,a1…是与t0=0的坐标相联系,则式(24)可简化为:

(25)
3.1.2 三次多项式拟合
与线性拟合推导方法相同,同理可得到三次多项式速度拟合系统误差公式:
Δvx=a5项+a7项+a9项+…
(26)
由式(25)、(26)可知,二次多项式拟合与线性拟合中点斜率相同(只有3次项系数以后的项),四次多项式拟合与三次多项式拟合中点斜率相同(只有5次项系数以后的项)。因此,二次多项式拟合的速度系统误差与线性拟合相同,四次多项式拟合的速度系统误差与三次多项式拟合相同。
3.2 加速度拟合的系统误差
与速度拟合求系统误差推导方法相同,二次多项式拟合求二阶导数获取的加速度系统误差表达式为:

(27)
如果坐标的初始值t0=0,那么式(27)可简化为:

(28)
四次拟合k次多项式求二阶导数的加速度系统误差推导方法与之类似,如果初始坐标系是t0=0,那么系统误差公式含有的项就只包括a6项,a8项……。也就是说,二次多项式拟合求加速度时,其系统误差与k次多项式a4项以后的偶数项相关;四次多项式拟合求加速度时,其系统误差与k次多项式a6项以后的偶数项相关。
3.3 速度拟合的随机误差


(29)

(30)
整理可得:
(31)

(32)

(33)
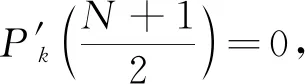
因此,式(33)进一步简化为:
(34)
从式(34)中误差的系数项可以看出,二次多项式拟合与一次多项式拟合的速度随机误差相同,四次多项式拟合与三次多项式拟合的速度随机误差相同。
式(34)中右边括弧里的项可表示为N的函数,由正交多项式递推公式和βk+1联合求解可得:
(35)
3.4 加速度拟合的随机误差
与速度拟合随机误差推导方法相同,同理可得k次多项式拟合段中点加速度表达式:
(36)
由式(36)中误差的系数项可以看出,三次多项式拟合与二次多项式拟合的加速度随机误差相同,五次多项式拟合与四次多项式拟合的加速度随机误差相同。
式(36)括弧内的前两项可表示为N的函数:

(37)
通过以上推导,得到了速度和加速度1~4次多项式拟合的系统误差和随机误差公式。结论总结如下:①对于速度拟合而言,二次多项式拟合的速度系统误差、随机误差均与线性拟合相同;四次多项式拟合的速度系统误差、随机误差与三次多项式拟合相同。②对于加速度拟合而言,二次多项式拟合的速度系统误差、随机误差均与三次多项式拟合相同;四次多项式拟合的速度系统误差、随机误差与五次多项式拟合相同。
下面以2004年11月16日11:59在酒泉地区获取的1次探测数据为例,根据上述推导结论,计算风场系统误差、随机误差及其不确定度。
4 个例分析
从实际探测获取的位移—时间曲线(图1)看,位置滑动拟合时(滑动拟合点数根据分层高度选取),采用3次多项式即可,即:
f(t)=a0+a1t+a2t2+a3t3
(38)
式中,f为纬向、经向和垂向分量。

图1 2004年11月16日11:59酒泉探空实测位移—时间曲线: (a)纬向,(b)径向,(c)垂向
4.1 雷达跟踪定位误差
雷达跟踪体制应答定位探空仪位置在站心坐标系中坐标计算公式为:
(39)
式中,x、y、z为探空仪位置点p在X、Y、Z轴上对应的坐标,单位:m;Rd为探空仪位置点p对应的雷达跟踪斜距,单位:m;α为探空仪位置点p对应的雷达跟踪仰角,单位:rad;δ为探空仪位置点p对应的雷达跟踪方位角,单位:rad;zh为探空仪的海拔高度,单位:m;h0为站心海拔高度,单位:m。
根据误差传递原理,雷达跟踪定位体制探空仪的定位误差为:
(40)
式中,σx、σy、σz为探空仪定位误差在站心坐标系X、Y、Z方向上的分量,单位:m;σR为雷达测距误差的标准差,单位:m;σγ为雷达测角误差的标准差,单位:rad。
采用常规高空气象702D雷达跟踪定位,其测距精度约为20 m,测角精度约为0.1°。由式(40)计算可得探空仪位置分量的定位误差曲线(图2)。可以看到,x方向(纬向)全程定位误差<60 m,y方向(经向)全程定位误差≤100 m,z方向(垂向)全程定位误差≤80 m。

图2 702D气象雷达跟踪定位误差曲线
4.2 速度和加速度拟合
与常规高空气象探测气球匀速上升不同,火箭探空仪在下落过程中,落速逐渐减小,探测数据点分布呈上疏下密,因此需根据垂直分层要求,将探测高度每10 km间隔,划分为50~60 km、40~50 km,30~40 km和20~30 km 4个高度区间,采用最小二乘法逐点对离散位置数据(x(t)、y(t)、z(t))进行滑动拟合。首先对位置数据进行线性拟合,分别求一阶导数获得速度(vx(t)、vy(t)、vz(t));然后对速度分量进行2次多项式拟合,求一阶导数获得加速度(ax(t)、ay(t)、az(t))。

根据实测数据分析(表1),50~60 km区间探空仪系统平均落速为87.6 m/s,摆动周期约为7 s,采用7点拟合(采样时间间隔Δt为1.05 s),拟合高度分辨率约为610 m;40~50 km区间宜取11点平滑,拟合高度分辨率约为570 m;30~40 km区间宜取21点平滑,拟合高度分辨率约为410 m;30 km以下区间宜取35点平滑,拟合高度分辨率约为275 m。根据对拟合误差的评估,通常采用线性、二次拟合平滑较为合适,即通过位置线性拟合求导获得速度,再对速度进行2次多项式拟合求导获得加速度。根据雷达定位数据拟合后的速度分量见图3。

表1 2004年11月16日11:59酒泉实测数据落速统计

图3 速度分量拟合曲线:(a)vx,(b)vy,(c)vz
4.3 拟合量系统误差和随机误差计算
速度采用线性拟合时,由式(25),其系统误差为:
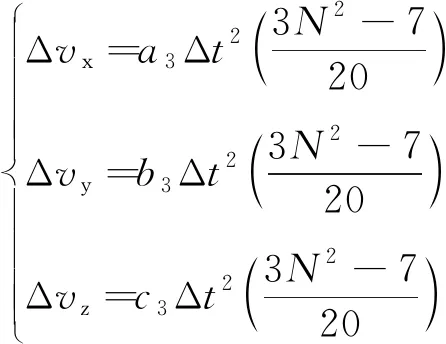
(41)

图4 拟合的速度分量系统误差:(a)Δvx,(b)Δvy,(c)Δvz
由于位置多项式方程的3次项(a3、b3、c3)未知,采用三次多项式最小二乘拟合系数代替。位置分量拟合系统误差见图4。可以看到,x方向(纬向)拟合系统误差基本在±1 m/s以内;y方向(经向)拟合系统误差50~60 km基本在±1.5 m/s以内,50 km以下在±0.5 m/s以内;z方向(垂向)拟合系统误差50~60 km约在±4 m/s以内,40~50 km约在±2 m/s以内,40 km以下约在±1 m/s以内。
加速度2次多项式拟合系统误差分量中含有a4项、a6项等,故加速度拟合系统误差为0。
由式(34),速度分量随机误差为:
(42)
加速度分量随机误差为:

(43)
速度和加速度随机误差曲线如图5、图6所示,图中速度和加速度误差存在阶跃变化的原因在于不同高度区间采取的拟合点数N不同。从图5可知,x方向(纬向)速度拟合随机误差在±1 m/s以内;y方向(经向)速度拟合随机误差基本在±2 m/s以内;z方向(垂向)速度拟合随机误差在±1.5 m/s以内。
速度拟合合成误差如图7所示,x方向(纬向)为±1.7 m/s,y方向(经向)为±3.3 m/s。

图5 拟合的速度分量随机误差:(a)σvx,(b)σvy,(c)σvz

图6 拟合的加速度分量随机误差:(a)σax,(b)σay,(c)σaz
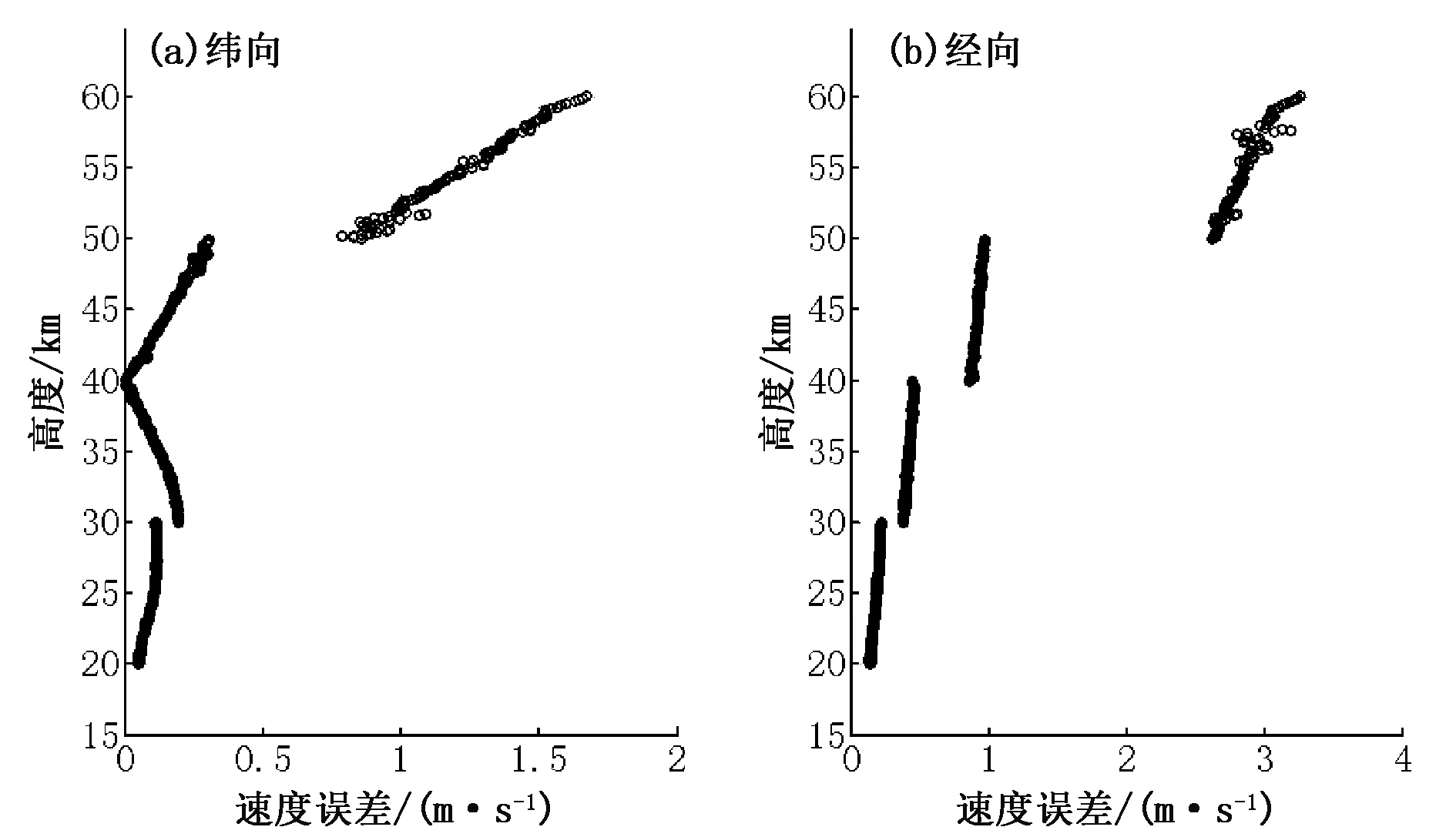
图7 拟合的速度分量合成误差:(a)Vx总,(b)Vy总
图8为修正后经纬向风速曲线,可以看到,在50 km以上经纬向风修正较大,50 km以下修正较小。

图8 修正后经向风(a)和纬向风(b)风速随高度变化
图9为临近空间20~60 km风场反演结果及不确定度曲线。可以看到,风速不确定度随高度降低而减小。表2、3、4为风速和风向反演结果及不确定度。可以看到,50~60 km为2.8~3.5 m/s,50 km以下在1 m/s以内。其中,在58.3 km高度风向不确定度异常增大到44.9°,31 km高度异常增大到18.1°,除风向0°渐变段(56~59 km,30~32 km)外,其他高度时基本在10°以内。
值得注意的是,风向在0°附近摆动时(此时风速也接近于0 m/s),会导致风向反演不确定度增大(图9框选部分)。

图9 反演风场及不确定度: (a)合成风风速,(b)风速不确定度,(c)风向,(d)风向不确定度

表2 风场反演不确定度

表3 50~60 km风向反演不确定度
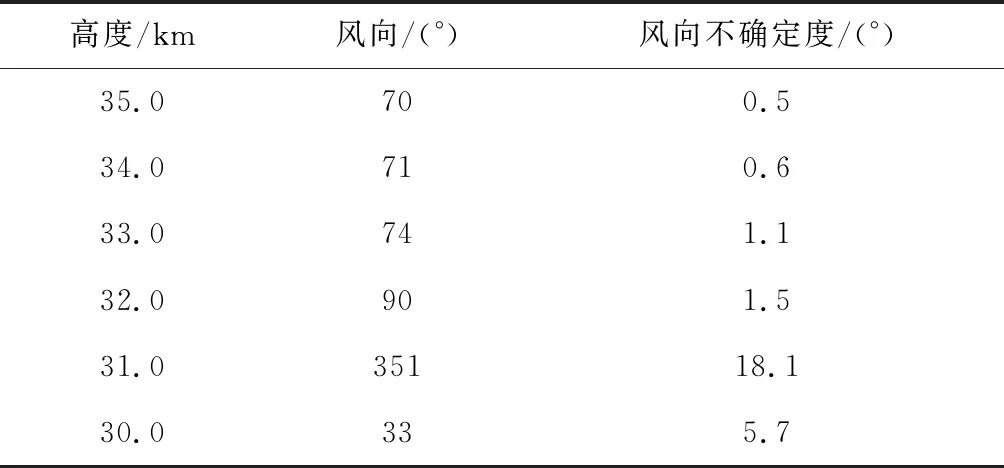
表4 30~35 km风向反演不确定度
5 结论
气象探空火箭探测临近空间风场是建立在探空仪位置获取的基础上,其反演误差来自雷达定位误差和拟合误差。雷达定位误差与自身定位精度、实际探测时仰角和斜距相关。因此,风场反演不确定的评估是基于多项式拟合和定位误差的分析,本文通过对多项式最小二乘拟合的误差分析研究,分别推导给出了系统误差和随机误差公式。采用一次实测数据计算表明,风速反演不确定度随高度降低而减小,50~60 km为2.8~3.5 m/s,50 km以下在1 m/s 以内;风向在0°附近摆动时(此时风速也接近于0 m/s),会导致风向反演不确定度异常增大,在其他高度时风向反演不确定度基本在10°以内。若采用更高精度的雷达,在高空大斜距条件下风场反演精度提升有限,而且会增加火箭探空仪结构设计的复杂性。若火箭探空仪采用导航卫星定位体制[12],获取的探空仪位置和实时速度在精度上会有量级上的提高,则可以极大地提升风场反演精度。

