Kersten-Krasil’shchik 耦合KdV-mKdV 方程的达布-贝克隆变换

高 鹏,薛玲玲

（宁波大学 数学与统计学院,浙江 宁波 315211）

Korteweg-de Vries(KdV)方程是孤立子理论中非常重要的方程.它有N=1[1]和N=2[2]超对称形式,当中N=2,a=1超对称KdV 方程为[2-6]:

其中,Di=∂/∂θi+θi(∂/∂x),(i=1,2)为超导数;Φ=Φ(x,t,θ1,θ2)是依赖于时间变量t、空间变量x及Grassmann 奇变量θ1与θ2的玻色函数.设Φ=v+θ2β,其中,β=β(x,t,θ1),v=v(x,t,θ1)分别是费米函数和玻色函数,式(1)可改写为N=1 的超对称形式:

其中,D≡D1.令β=θ1u(x,t),v=w(x,t),式(2)退化为经典方程:

当w=0时,式(3)约化为KdV 方程ut=(-uxx+3u2)x;当u=0时,式(3)约化为wt=-wxxx+3w2wx和(wwxx)x=0,前者是mKdV 方程.因此,人们将方程(3)称为Kersten-Krasil’shchik 耦合KdV-mKdV方程[7].此外,令w=iφ,u=-φx(i2=-1),式(3)还可约化为3 阶Burgers 方程φt=-(φxx+3φφx+φ3)x.

耦合KdV-mKdV 方程(3)的很多性质已被研究.Kersten 和Krasil’shchik 证明该方程完全可积性,即存在递推算子和无穷多对称[7].随后,Kalkanli 等[8]证明它具有Painlevé 性质和Lax 对,Hon 等[9]获得了它的孤子解和双周期波解,Qin 等[10]得到了它的双线性形式并给出了N-孤子解.最近,Rui 等[11]构造了它的拟周期解,Qasim 等[12]得到了近似解.但据我们所知,它的达布变换和贝克隆变换尚未被研究.

达布变换在孤立子理论和可积系统的研究中起着至关重要的作用,其可以有效地构造出非线性系统不同形式的精确解[13-14].由达布变换可推导出贝克隆变换,即从一个已知解出发对贝克隆变换积分求得新解.依据Bianchi 的可交换性定理,由贝克隆变换可以生成非线性叠加公式,从而只需通过微分和代数计算便可以求出新解[15].本文将从耦合KdV-mKdV 方程的矩阵形式的线性问题出发,作规范变换推导达布变换和相应的贝克隆变换,进而构造非线性叠加公式,从而为进一步研究式(3)的解和构造式(1)的达布变换和非线性叠加公式提供理论基础.

1 达布变换

方便起见,引入变量φ和φ使得w=iφx,u=-φx.由式(3)得到势KdV-mKdV 方程:

由式(2)的Lax 对[6]可以得到式(4)的Lax 对:

fx+φxg-λf=0,

其中,λ为谱参数.引入变量h使得hx=gφx+φxfx,并令Ψ=[f,g,h]T,式(5)可改写为矩阵形式:

其中,

可以验证式(6)的相容性条件,即零曲率方程

等价于式(3).注意到,通过规范变换[13]:

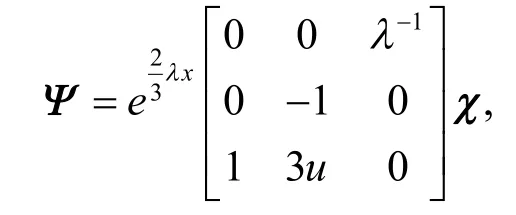
式(6)等价于文献[10]给出的Lax 对.

接下来,构造线性系统(6)的达布变换.假设存在一个规范变换:

使得～Ψ满足:

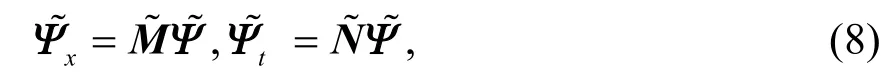
假设待定矩阵T关于λ是一次的,即T=λH+G,其中,H和G是与λ无关的 3×3 矩阵,并且将M改写为:

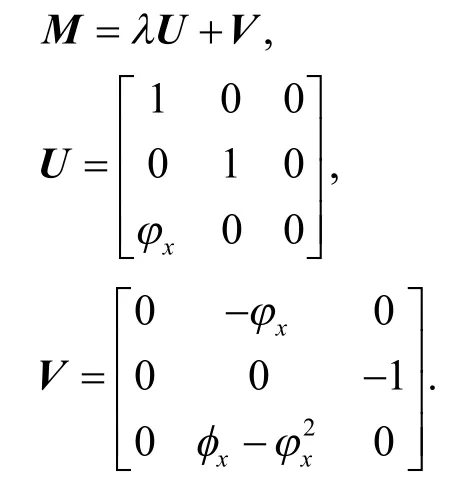
比较式(9)第1个式子中λ的各次幂系数,得到矩阵方程:

由式(10)可得:

其中,c、s、hij和gij是待定函数,且满足以下超定方程:

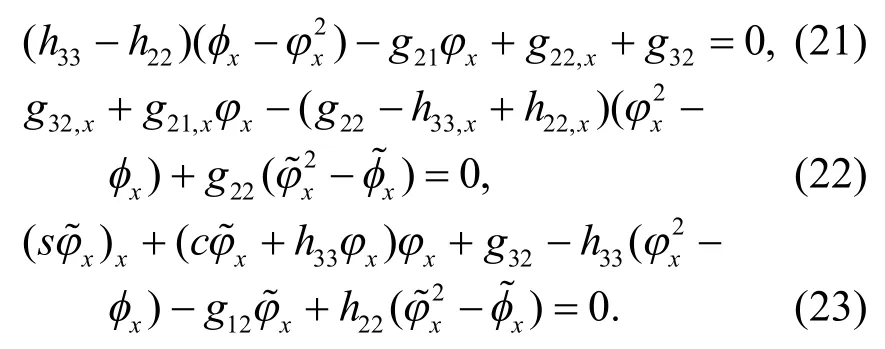
由式(11)知h33为常数.不失一般性,取h33=1.

为得到简洁的达布矩阵,取式(15)的特解,即g21=0.再由式(14)可得g11=k1,其中,k1是积分常数.

将式(16)和式(19)相加,式(17)和式(18)相减,分别得到:

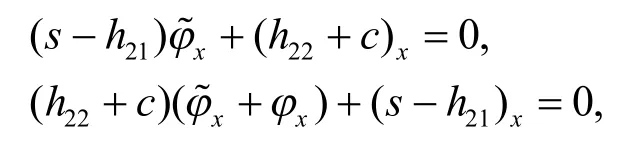
取其特解:

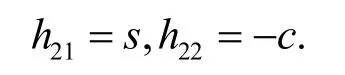
此时式(16)和式(17)可分别化为:

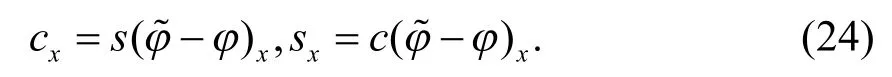
引入辅助变量r,使得

并取式(24)的特解:

下面将r和其他未知变量用线性系统(6)的解来表示.取Ψ1=[f1,g1,h1]T是线性系统(6)当λ=λ1时的解.特别地,由式(6)的第1 个矩阵方程得:

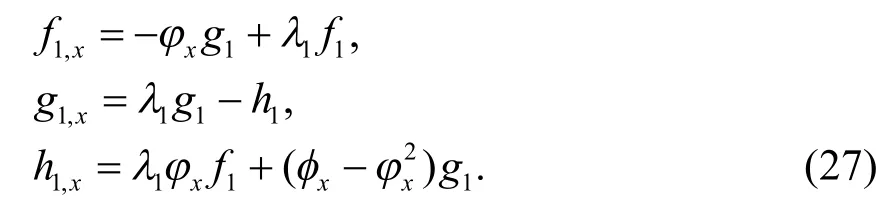
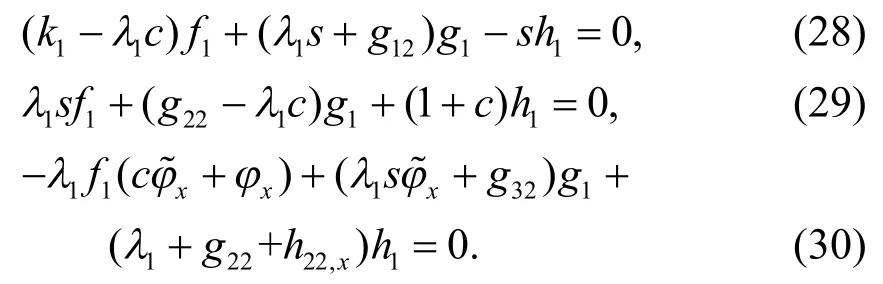
先求解式(28).

将式(12)整理为:

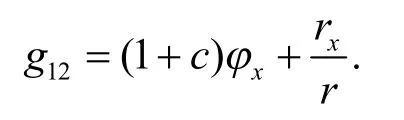
为了从式(28)中求出r,拟设r=r(f1,g1).利用式(27)的前2 个式子,g12的表达式可改写为:

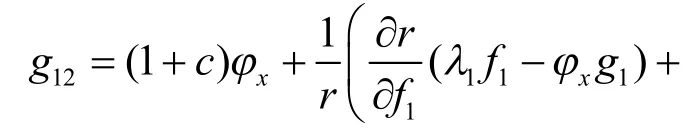
将式(31)代入式(28),并比较φx和h1的系数,分别得到以下方程:

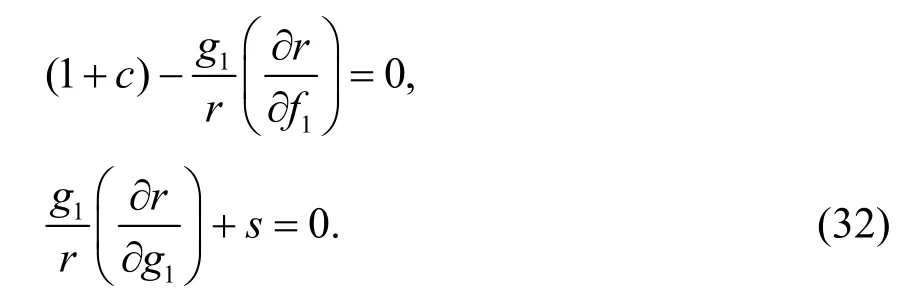
式(32)的解为:

其中,k2是积分常数.将式(33)代入式(28),可得k1=-λ1.

然后,求解式(29)和式(30),分别得到:

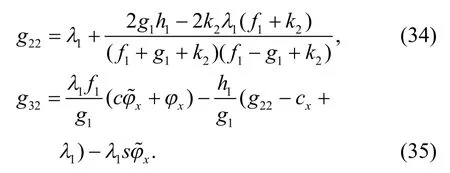
利用式(25)、(26)、(33)和(34),比较式(13)和式(35)可得:

最后,由式(20)可得k2=0.可以验证式(21)～(23)成立,式(9)的第2 个矩阵方程也成立.我们将结果整理为以下定理.

定理1设Ψ1=[f1,g1,h1]T是线性系统(6)当λ=1λ时的解,定义

其中,

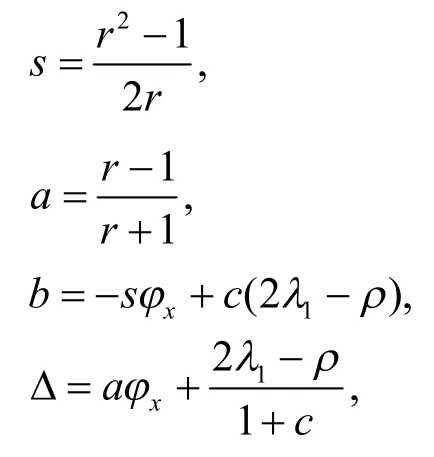
则式(7)满足式(8).其中,T是达布矩阵.

需要说明的是,为了给下一节做铺垫,式(38)中的达布矩阵T已经用辅助变量r和ρ来表示,即线性系统(6)的解以及φ.下面我们用场变量φ、φ、来表示达布矩阵T.利用式(36)和式(37),把辅助变量r和ρ改写成:

同理,由式(9)的第2 个矩阵方程可得耦合KdV-mKdV 方程时间部分的贝克隆变换:

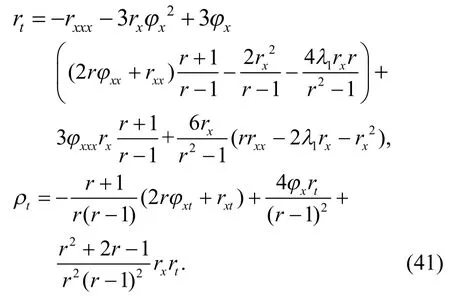
2 非线性叠加公式

贝克隆变换式(40)和(41)建立了势耦合KdVmKdV 方程(4)的新解与旧解(φ,φ)之间的联系.从一个已知解出发,对贝克隆变换进行积分一次就可以得到新解,但构造大量的新解有一定困难.由达布-贝克隆变换的可交换性可获得非线性叠加公式,利用它只需通过微分和代数运算便可以得到新解[14].

利用达布变换(7)以及式(38)和式(39),我们考虑一对达布变换:

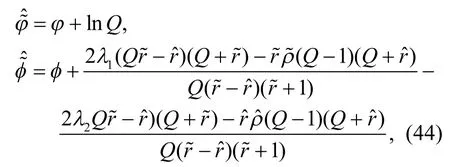
其中,

因此,对于给定方程(4)的3 组解(φ,φ)、和,利用式(44)便可以得到新解.