全应力-应变条件下气体钻井井壁稳定性研究

朱忠喜，白宗玺，李光乔，雷万能

1.油气钻井技术国家工程实验室防漏堵漏技术研究室(长江大学)，湖北 武汉 430100 2.长江大学石油工程学院，湖北 武汉 430100 3.中国石化西北油田分公司工程技术研究院，新疆 乌鲁木齐 830011 4.中国石油塔里木油田分公司油气田产能建设事业部，新疆 库尔勒 841000

气体钻井技术有利于提高钻井速度，避免井漏，克服地层水敏等问题。气体钻井过程中，由于井眼内气体对井壁支撑较弱，井眼在原地应力作用下不可避免地会出现形变。因此需要根据气体钻井时的井壁实际受力情况进行井壁稳定性评价。国内外学者在进行气体钻井中井壁稳定分析时多沿用了钻井液钻井条件下的方法，即按照井壁围压达到弹性极限状态来计算坍塌压力[1-5]，借用钻井液钻井坍塌压力的评估模型，按照弹性极限状态来进行应力分析并与井壁岩石的强度比较。但这些力学分析的假设条件都是岩石达到峰值强度后完全丧失承载能力[6]。然而，工程实践表明，即使井周围岩发生了破裂，但仍能够维持稳定、安全的工作[7-10]。这表明岩石不仅在破坏前承受载荷，而且破坏后仍具有一定的承载能力，岩石全应力-应变过程能更加真实地反映出岩石的承载和变形特性。但岩石全岩应力-应变模型描述过于复杂，不利于对工程问题的分析,为此,笔者结合前人经验，将岩石全应力-应变模型简化为弹性、塑性软化和残余3个线性阶段[11，12]，对井壁围岩的应力状态进行分析。同时，由于气体的可压缩性使得气体在井筒内流动过程的温度和压力变化更加复杂[13-17]，尤其是在钻头处会发生焦耳-汤姆逊效应，气体经过喷嘴后产生较大温降，从而在井筒尤其是井底附近的井段井壁温度较低，井壁会出现较大的热应力[16-19]，这对井壁围岩的受力状态也将产生较大影响。因此，在进行井壁围岩应力分析建模时也考虑了井壁热应力作用。

1 岩石理想弹塑性软化模型

岩石材料的全应力-应变关系曲线(见图1(a))可简化为最简单的折线形式(见图1(b))，即为理想的弹塑性软化模型(见图中a-c-f折线)。把岩石的变形过程分为弹性变形、塑性软化变形和残余变形3个阶段[11]。弹性变形时的弹性模量为E，塑性软化变形时的软化模量为Ep，则脆性系数β=Ep/E。

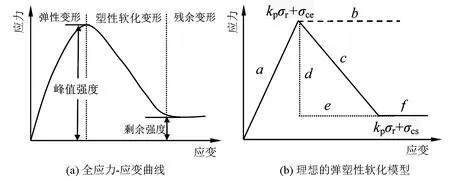
图1 岩石全应力-应变关系Fig.1 Relationship of complete stress-strain of rock

1.1 弹性变形阶段岩石强度

岩石在弹性变形阶段服从虎克定律，在屈服时满足摩尔-库仑准则[20,21]，于是有:

(1)

式中：σθ、σr分别为周向和径向应力，MPa;σce为弹性变形阶段单轴抗压强度，MPa;φ为岩石弹性变形阶段内摩擦角，(°)。

1.2 塑性软化变形阶段岩石强度

岩石强度随变形发展而衰减主要是受内聚力变化的影响，其强度可表示为：

σθ=kpσr+σcp

(2)

式中：σcp为塑性软化变形阶段受内聚力变化影响的单轴抗压强度，MPa。

1.3 残余变形阶段岩石强度

在残余变形阶段，岩石的强度降到最低值，其强度可表示为：

σθ=kpσr+σcs

(3)

式中：σcs为单轴压缩的残余强度，MPa。

2 原地应力引起的井周应力

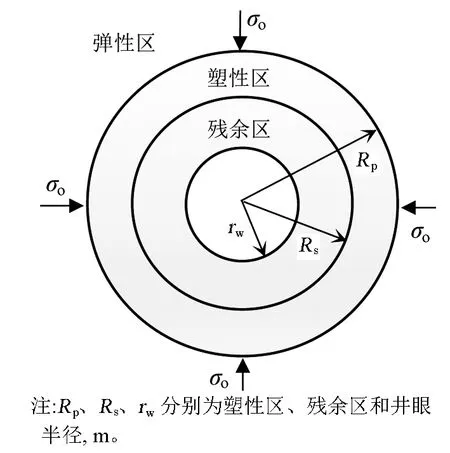
图2 井周围岩变形分区Fig.2 Division of rock deformation around wells

假设岩体为各向同性、均质的连续介质，在水平井平均应力σo的作用下井眼处于平面应变受力状态，其对应的平衡方程[22]为：

(4)

式中：r为径向坐标，m。

随着水平平均应力σo逐渐增加，井眼周围的岩石由外向内依次为弹性区、塑性区、残余区(见图2)。若当水平平均应力σo较小时，可能只出现弹性区。

2.1 弹性区的应力

根据弹性理论可知，弹性区应力为：

(5)

(6)

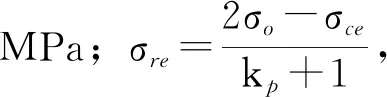
2.2 塑性区的应力

塑性区强度衰减规律式(2)可由式(6)表示:

(7)

式中：ν为泊松比，1。

由体积不可变、弹塑性交界处的径向位移连续条件和边界条件可知，当r=Rp时，σr=σre，可得塑性区应力为：

(8)

2.3 残余区的应力

在塑性区与残余区交界处，当r=Rs=λRp时，σcp=σcs，代入式(9)则有:

(9)

式中：Rs为残余区半径，m;λ为残余区半径与塑性区半径之比。

在塑性区和残余区交界处径向应力具有连续性，故以r=Rs代入式(11)求得的径向应力作为边界条件。将式(9)和式(3)所表示的残余强度代入平衡方程式(4)并积分，结合边界条件即可求出残余区应力：

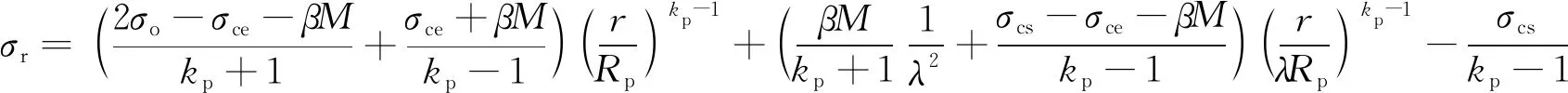
(10)

3 井周热应力

气体钻井时，将井筒内的传热过程视为稳态传热，而将井壁外侧地层内传热视为非稳态传热。钻柱和环空内气体流动数学模型可以用质量守恒、动量守恒和能量守恒方程表示:

(11)

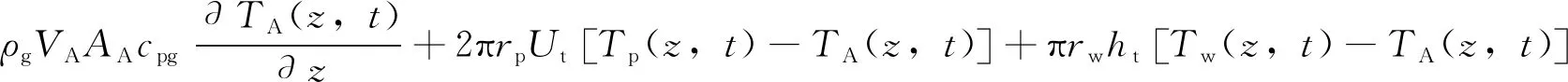
(12)

(13)

式中：ρg、ρf分别为气体和岩石密度，g/cm3;Vp、VA分别为钻柱内和环空内流体速度，m/s;Ap、AA分别为钻柱内和环空流体过流断面面积，m2;cpg、cpf分别为气体和岩石比热，J/(kg·℃);Tp、TA、Tw分别为钻柱内流体、环空流体、井壁岩石温度，℃;Ut为钻柱内到井壁岩石之间的总传热系数,J/(s·℃·m);ht为井壁岩石传热系数，J/(s·℃·m);kf为地层导热系数,J/(h·℃·m);r、rp分别为径向坐标、钻柱半径,m;t为时间变量，s;z为井深，m。

钻井过程中，钻井液循环会造成井眼周围温度发生变化，此时会产生一个附加应力场。对于均质各向同性、多孔热弹性地层，由热传导理论和热弹性力学可得到井周温度变化引起的井周附加应力，其表达式为：

(14)

(15)

其中：

Tf(r,t)=T(r,t)-T0Tw(t)=T(rw,t)-T(rw,0)

式中：σrT、σθT分别为地层温度变化引起的井周径向、周向、轴向附加应力分量，MPa;E为地层弹性模量，MPa;α为地层体积热膨胀系数，1/℃;Tf(r,t)为井周地层温度变化分布函数;Tw(t)为在井壁处钻井液温度,℃;T0为地层原始温度，℃。

4 塑性区半径和残余区半径的确定

4.1 塑性区半径

在考虑原地应力和热应力共同作用下，若围岩变形刚好处于塑性变形完成，但还未出现残余变形的临界状态，此时的塑性区半径为Rpc，则由边界条件r=rw时，σce=σcs，σr=pi，将式(7)代入式(8)并与式(14)结合，可得:

(16)

式中:Rpc为塑性区临界半径，m;pi为井筒内气体支撑力，MPa。

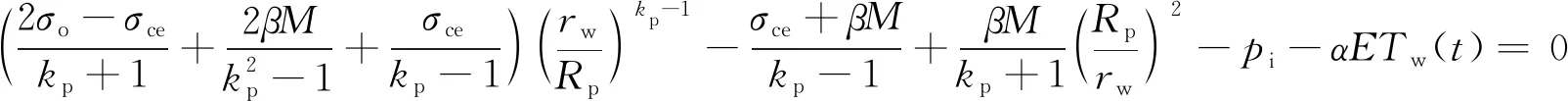
(17)

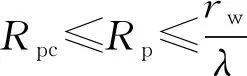
4.2 残余区半径

当井壁围岩达到完全塑性后会继续向残余区扩展，此时将边界条件r=rw时σr=pi代入式(10)可得：

(18)

Rs=λRp

(19)

5 模型验证

气体钻井时，判断井壁围岩稳定性，可以通过实测井眼半径与模型中计算的井周围岩塑性半径的比较来进行。若井壁围岩的塑性半径变化趋势与实测井眼半径接近，可以间接验证模型的准确性。

以新疆油田HB021井为例对模型进行检验和分析。该井实施气体钻井井段为1000～2200m，井径曲线如图3所示，其施工参数及热力学参数如表1所示。根据井筒流动和传热模型计算的井筒压力和温度分布如图4和图5所示。根据模拟计算的井筒压力和温度参数，应用井壁围岩应力模型分别计算了在不考虑热应力和考虑热应力影响时的井壁围岩各应力状态下对应的半径，具体如图6和图7所示。

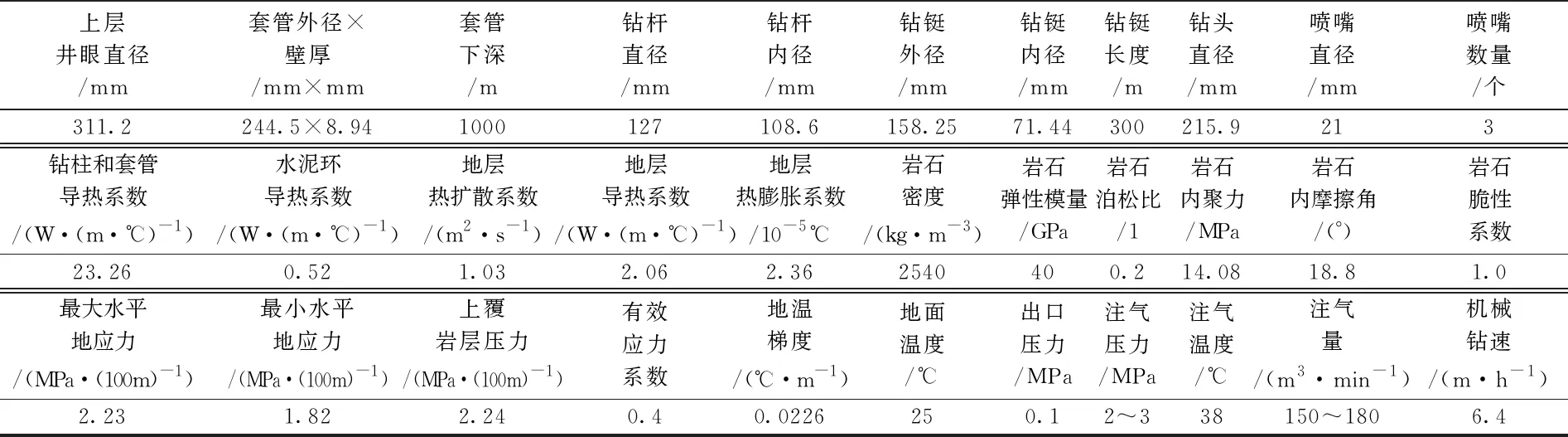
表1 HB021井施工参数及热力学参数Table 1 Construction parameters and thermodynamic parameters of well HB021

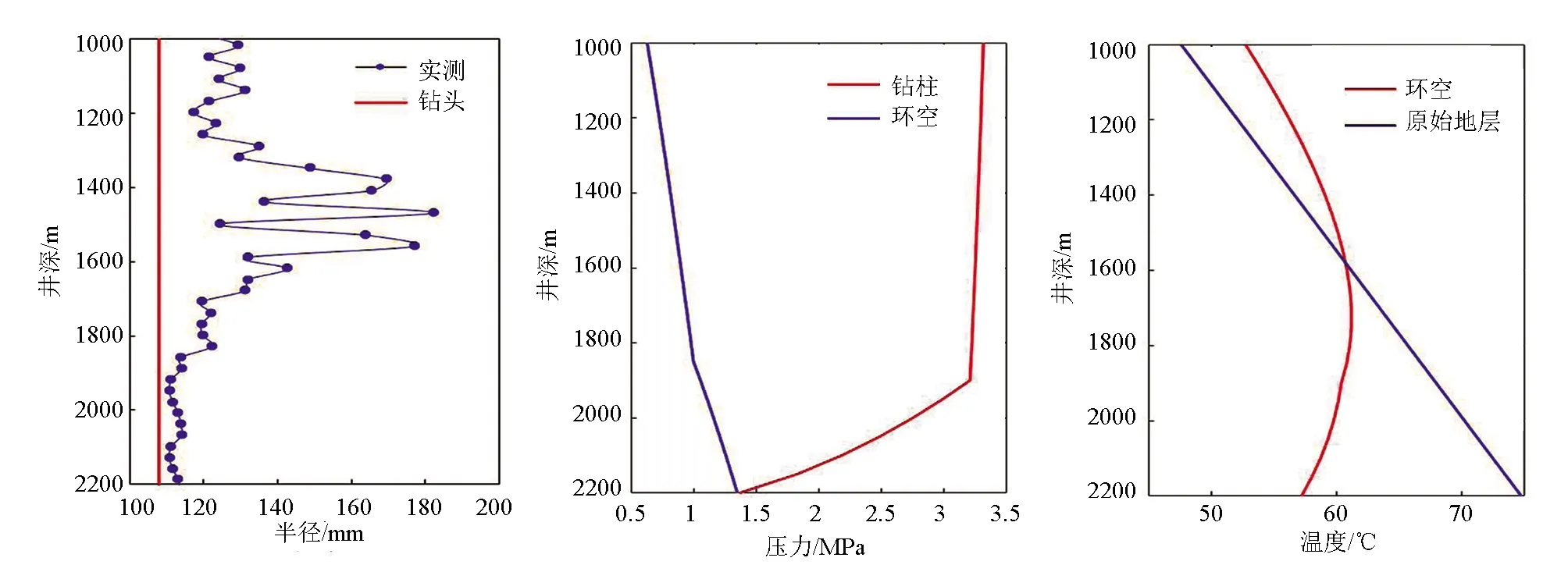
图3 实测井眼半径 图4 气体钻井井段压力分布 图5 气体钻井井段温度分布Fig.3 Measured borehole Fig.4 Pressure distribution in gas Fig.5 Temperature distribution radius drilling section in gas drilling section

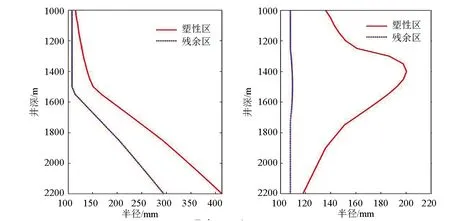
图6 不考虑热应力作用时的井眼变形 图7 考虑热应力作用时的井眼变形Fig.6 Borehole deformation without Fig.7 Wellbore deformation con- considering thermal stress sidering thermal stress

井壁围岩处于弹性区，井壁围岩的稳定性较强;当井壁围岩处于塑性区时，井壁围岩处于稳定向不稳定的过渡阶段;当井壁处于残余区时井壁已经失稳。气体钻井时，井筒内气流压力非常小，对井壁的支撑力很弱，井壁围岩的受力状态主要受原地应力影响，若井壁围岩出现残余区，那么井壁呈现不稳定状态;若井壁围岩没有出现残余区，而处在塑性区，那么井壁围岩处于稳定状态向不稳定状态的过渡状态，并且随着钻井时间增长，气流对井壁的冲刷作用，使井壁围岩通过产生一定的破损，增大井径，使井壁进入稳定状态。图3中显示，在1300～1600m井段处，井眼扩径严重，井壁垮塌剧烈，说明在该井段井周围岩塑性区半径较大;在1000～1300m处的井眼半径高于下部1600～2200m处的井眼半径，说明上部地层的井周围岩塑性区半径要大于下部地层的半径。

由图4可知，气体钻井时环空内的气流压力较低，上部井段压力在1MPa以内。由图5可知，气体钻井时环空内气体在井底附近的温度与原始地层温度相比，降低的幅度达到17.5℃。随着气体向上流动，逐渐被地层加热,温度升高，在1600m附近与地层温度相等，随后环空内气流温度略高于地层温度。这也就意味着，在气体钻井过程中，随着钻进过程的推进，井壁处岩石都会经历一个被冷却，之后逐渐恢复至原始地层温度，最终达到略高于原始地层温度的过程。

由图6可知，当不考虑热应力作用时，气体钻井井段的井壁围岩塑性区半径是上部小、下部大，并且在1700m以下塑性区半径增大较快，在2200m以下产生的残余区开始逐渐增大。但是与图3进行比较，显示在不考虑热应力作用时，计算结果与实际情况不相符。对比图7和图3，二者的计算结果基本相符。这说明在考虑热应力作用时，全岩应力-应变计算模型更加符合现场实际。

根据图6和图7对比分析可知，不考虑热应力影响，井底处的塑性半径远高于考虑热应力影响时的塑性半径;而在上部井段影响情况相反。其原因可以从图5中的温度分布情况进行分析：在井底附近，井筒温度远低于地层原始温度，井壁产生的热应力对井壁岩石起到收缩的效果，抵消了一部分井壁围岩在地应力的作用下向井筒内膨胀的作用;而在井眼上部，由于井筒温度高于地层温度，井壁岩石在热应力的作用下发生膨胀，增强了井壁围岩向井筒内膨胀的作用。因此，井眼下部热应力对井壁稳定性起到强化效果，而上部井段起到了加剧井壁不稳定的效果。

6 结论

1)根据理想弹塑性软化模型，将岩石全应力-应变过程简化为弹性、塑性软化和残余3个线性阶段，并应用到气体钻井井壁稳定性分析中。将井周围岩变形划分为弹性区、塑性区和残余区，可更加方便直观地描述井周岩石的受力和变形情况。

2)理想弹塑性软化模型得出的塑性区半径具有一定的普适性，理想弹塑性模型和理想弹脆性模型计算的塑性区半径可以由理想弹塑性软化模型简化来获得。

3)气体钻井时钻头喷嘴处会发生焦耳-汤姆逊效应，导致井筒温度分布不同于原始地层温度，井壁岩石会产生热应力。热应力对井周岩石的应力场产生较大影响，一般来说，在井筒下部热应力起到增强井壁稳定性的效果，而在上部则会增加井壁的不稳定性。