基于动态神经网络的喷雾耙供气温度数据重构

赵 照，熊建军，冉 林，何 苗

(中国空气动力研究与发展中心结冰与防除冰重点实验室，四川绵阳 621000)

0 引言

飞行器穿越含有过冷水滴云层时，其机体表面会出现结冰现象，严重影响飞行安全[1-2]。结冰风洞作为重要的地面模拟设施，被广泛应用于结冰与防除冰试验研究中[3]。喷雾系统是结冰风洞的关键配套设备，用于模拟飞行器穿越含有过冷水滴云层时遇到的高空云雾环境，由喷雾耙架、供气系统、供水系统等组成[4]。供气系统将高压气源通过减压、加热、过滤等一些操作后，经调压进入喷雾系统喷雾耙内，喷雾耙内供气管路布置一支温度传感器用于测量耙内气体温度。喷雾耙内低温潮湿的恶劣环境经常造成温度传感器损坏，导致试验过程中的喷雾耙供气温度参数缺失，影响试验数据分析。因此，实现传感器故障期间喷雾耙供气温度数据重构具有重要的研究意义和工程价值。

结冰风洞喷雾供气系统是高度耦合的热力系统，喷雾耙供气温度是时变的，全时段的供气温度构成了一个受多种因素影响的复杂非线性时变系统，其复杂时变热力耦合关系难以用准确的物理模型进行描述。神经网络(neural network，NN)作为一种利用数据驱动的算法[5]，其利用非线性映射和并行处理方法，通过不断学习和训练，完成输入与输出之间的映射关系，在误差分析[6]、数据预测与重构[7-10]、故障检测与诊断[11-15]等领域得到了应用。上述文献中采用的神经网络是一种前馈神经网络，适用于输出仅与当前输入有关的模型，而喷雾耙供气温度的变化具有滞后性，与之前的温度存在关联性，使得其在数据重构上存在很大局限性。动态神经网络具有反馈与记忆功能，可存储内部状态，从而使神经网络能够适应动态系统变化，克服前馈网络不具备动态特性的缺点。近些年来，被广泛应用于数据预测[16-20]、故障检测[21-22]等领域。例如，文献[16]中利用动态神经网络对高速铁路沉降预测问题进行了研究。文献[17]中利用动态神经网络对风电机组齿轮油温的趋势进行了预测。文献[20]采用动态神经网络对天气预报问题进行了研究。上述文献中都表现出动态神经网络具有优异的动态特性及建模效果。

文中针对喷雾耙供气温度数据重构问题，首先采用主成分分析(PCA)获得了喷雾耙供气温度真实影响因素，建立了一种基于动态神经网络喷雾耙供气温度数据重构方法，并提出了单点数据异常与长期数据异常的重构策略，对数据重构方法有效性进行了验证。

1 喷雾耙供气温度描述

1.1 喷雾耙供气系统

喷雾供气系统由手动球阀、电动球阀、过滤器、气体电加热器系统、气路电动调节阀、电动球阀和排水阀等组成，如图1所示。气源为高压气体，经减压后引入供气系统，经过手动球阀、电动球阀与过滤器，然后进入电加热器系统加热气体温度，由气路电动调节阀调压后经电动球阀进入喷雾耙，喷雾耙内供气管路上布置1支压力传感器与1支温度传感器。

图1 供气系统结构图

1.2 喷雾耙供气温度影响因素

喷雾耙位于结冰风洞稳定段内，处于低温潮湿环境，且喷雾耙入口温度传感器与喷雾耙内温度传感器距离较远，管道的热损失导致喷雾耙供气温度与喷雾耙入口温度差异较大，无法直接通过入口温度得到喷雾耙供气温度。结冰风洞试验过程中会产生大量数据，且各变量间具有一定的关联度，因此需要对试验数据进行预处理，得到喷雾耙供气温度的真实影响变量。

PCA作为一种数据降维算法被广泛应用于消除冗余数据，PCA的主要思路是通过特征提取，消除变量之间的冗余信息，生成独立的数据，步骤如下[23]：

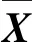
(3)根据各个主成分贡献率Qi进行排序，保证前q个主成分贡献率的代数和Qs大于85%即可。

(1)

(2)

通过PCA分析之后，得到喷雾耙供气温度Ta的变化主要与喷雾耙入口温度tin、喷雾耙供气压力pa和风洞内环境温度Tt有关，如图2所示，根据历史数据分析可知：

(1)喷雾耙入口温度升高，热空气经管道传输后到达喷雾耙供气管道，喷雾耙供气温度随之升高，反之，喷雾耙供气温度降低；

(2)喷雾耙供气压力升高，由于前段加热器反应不及时，喷雾耙入口温度降低，喷雾耙供气温度升高，反之，喷雾耙入口温度升高，喷雾耙供气温度降低；

(3)风洞内环境温度升高，位于稳定段内的喷雾耙整体温度升高，导致喷雾耙供气温度升高，反之，热损耗增加，喷雾耙供气温度降低。

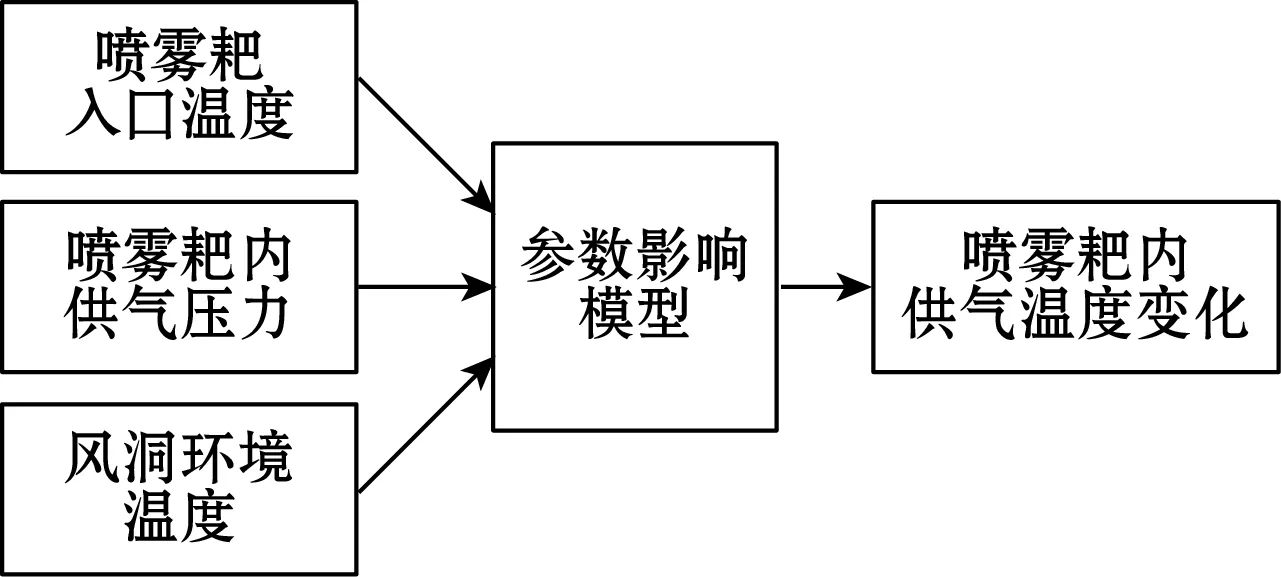
图2 供气温度影响模型

2 动态神经网络建模

2.1 动态神经网络简介

神经网络是一种模拟动物神经网络以实现类人工智能的机器学习方法[5]，根据网络结构，分为静态神经网络与动态神经网络。静态神经网络一般指没有反馈与延迟单元的前馈神经网络，其输出仅与前馈输入有关。动态神经网络是具有记忆功能的神经网络，其输出不仅与当前输入有关，还与历史输入和输出有关。喷雾耙供气温度变化是个动态的过程，采用静态神经网络将会出现学习收敛速度慢、动态反应差的问题，而动态神经网络具有记忆功能，可以更直接反映系统动态特性。

文中采用带有外部输入的非线性自回归动态神经网络对喷雾耙供气温度进行数据重构，具有3层结构，分别为输入层、隐藏层与输出层，动态神经网络的框架如图3所示，下一时刻的预测值是关于输出历史值与输入变量的非线性映射。

图3 动态神经网络框架

2.2 供气温度神经网络建模

由1.2节可知，喷雾耙供气温度的变化值与喷雾耙入口温度Tin、喷雾耙供气压力pa和风洞内环境温度Tt有关，则喷雾耙供气温度Ta为其历史值加上变化值，因此，供气温度参数重构模型是一个多输入单输出系统，且输出与输入、历史输入与输出都有关联，采用带有外部输入的非线性自回归动态神经网络建立的重构模型可表示为：

X(t)={Tin(t),pa(t),Tt(t)}

(3)

Y(t)=Ta(t)

(4)

Y(t)=f[X(t-1),…,X(t-n),
…，Y(t-1),…Y(t-n)]

(5)

式中：X(t)为输入变量；Y(t)为输出变量；n为历史输入/输出变量个数。

根据供气温度神经网络模型可知，神经网络有3个输入变量(Tin、pa与Tt)和1个输出变量Ta。根据Funahashi定理可知[24]，3层神经网络即可实现在闭集对任意的非线性映射进行逼近，且隐藏层神经元个数可参考式(6)。因此，神经网络隐藏层数量选取为1，隐藏层神经元个数经过多次训练设置为10个，历史输入/输出变量个数n选为2。输入层与隐藏层的激活函数选取tansig函数，隐藏层与输出层的激活函数为purelin线性函数。

(6)

式中:m为隐藏层神经元个数；p为输入变量个数；q为输出变量个数；a取值为1～10。

选用Levenberg-Marquardt算法训练神经网络，并选取均方误差函数(mean squared error，MSE)作为神经网络误差函数，如式(7)所示。

(7)

式中：et为单个误差；y(t)为实际值；yc(t)为预估值；N为时间序列数。

3 模型验证与分析

3.1 数据选取与模型训练

采用结冰风洞试验的8天历史数据用于喷雾耙供气温度数据重构建模。选取前6天历史数据用于模型训练，并用训练好的模型对后2天喷雾耙供气温度进行数据重构分析，验证动态神经网络的泛化能力。

试验数据可以分为2种排序训练方法进行动态神经网络训练，分别为序列排序与并行排序。序列排序是指6天历史数据按照时间顺序排列，后一天的第1组数据与前一天的最后一组数据相连，如图4所示；并行排序是指6天数据按照并行方式排序，第1组数据初始时间一致，如图5所示。下面分别采用序列排序与并行排序方式对喷雾耙供气温度神经网络模型进行训练。

图4 序列排序

图5 并行排序

图6与图7分别展示了序列排序与并行排序神经网络训练收敛图与相关性曲线，其中，图6(a)与图6(b)横坐标轮次是指所有数据通过神经网络的次数，曲线中圆圈处为验证数据误差达到最低时的位置。表1是2种排序方法的训练效果对比数据。

表1 序列排序与并行排序误差分析

由图6、图7和表1可知，并行排序方式相比序列排序方式，MSE与最大绝对误差较小，线性相关度较高，因此，数据重构采用并行排序方式进行动态神经网络训练可取得较好效果。

(a)序列排序

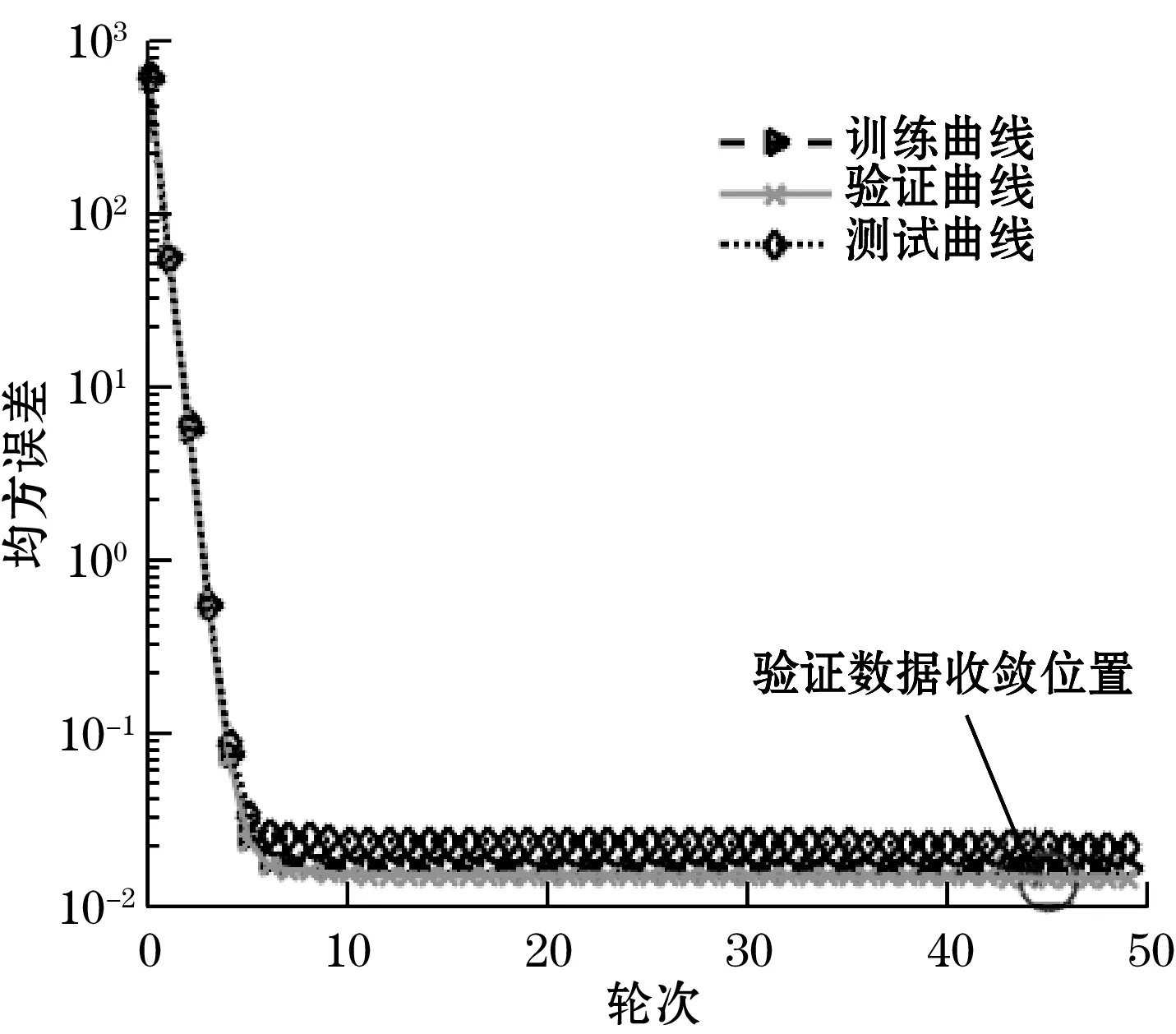
(b)并行排序图6 动态神经网络收敛图

(a)序列排序

(b)并行排序图7 相关性曲线

3.2 单点异常数据重构分析

试验过程中，喷雾耙供气温度传感器采集的数据偶尔会出现单点异常，针对这种单点异常数据的重构，需要利用单步预测，即通过输入变量历史真实值与输出变量历史真实值预测异常点输出变量，接着更新下一个异常数据之前的所有真实输出变量数据，直至预测完所有输出变量，即完成单点异常数据重构。

选用后2天试验数据进行单点异常数据重构分析，图8与图9展示了后2天单步喷雾耙供气温度数据重构预测值与真实值的对比曲线。表2是单步预测数据重构误差分析。由图8、图9与表2可知，第7天与第8天的均方误差分别为0.009与0.018，单步预测预测值与真实值误差较小，曲线拟合程度较高，训练后的动态神经网络具有很强的泛化能力。

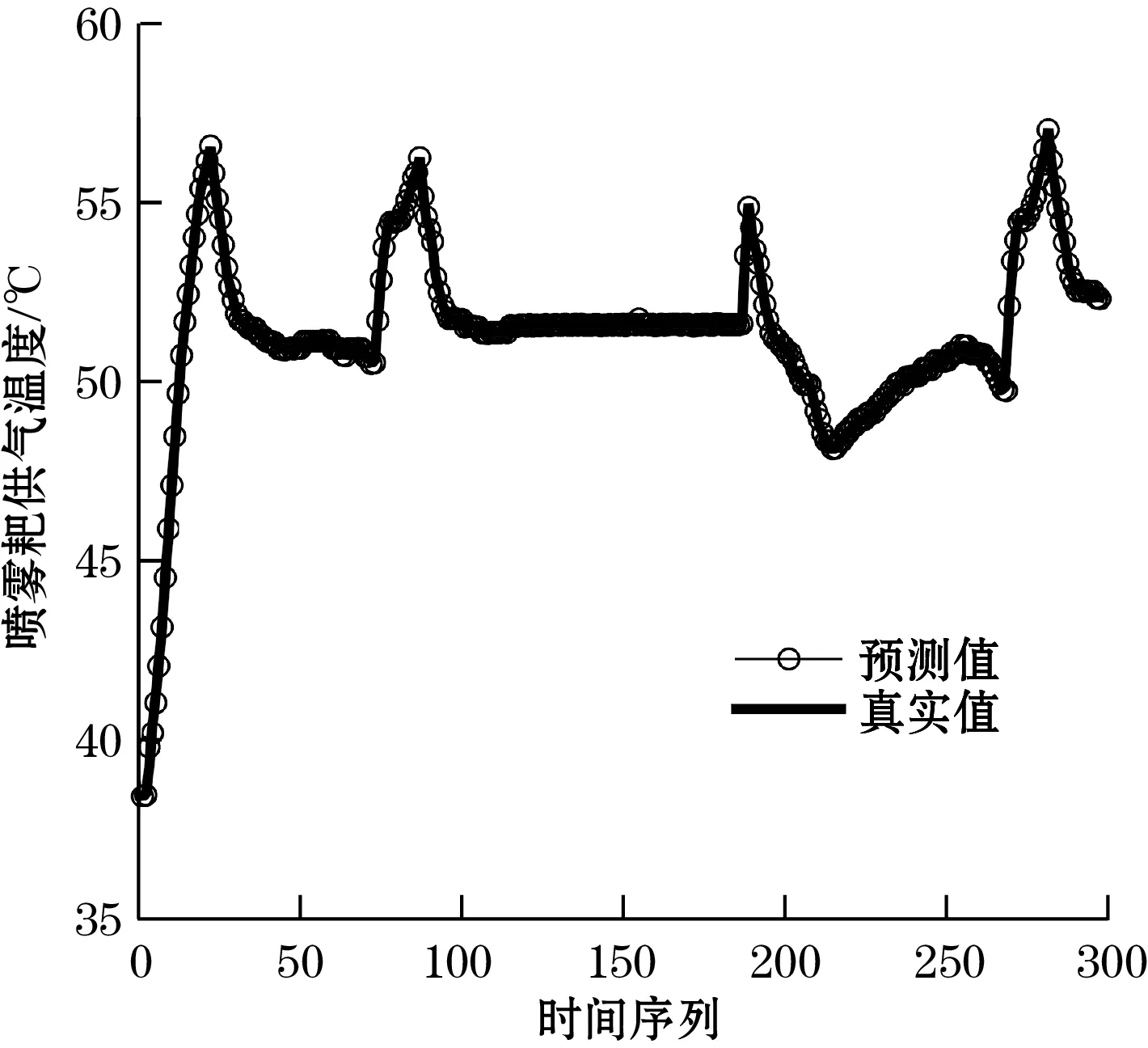
图8 第7天供气温度单点数据重构

图9 第8天供气温度单点数据重构

表2 单点数据重构误差分析

3.3 长期异常数据重构分析

除了喷雾耙供气温度数据出现短期异常的情况，若试验过程中供气温度传感器损坏，则会出现该次试验数据长期异常的情况。此时，喷雾耙供气温度数据在传感器损坏后的数据全部无法使用。针对长期异常数据重构问题，首先以输入变量历史数据与输出变量数据异常前的数据预测当前输出变量值，在预测数据后，将该数据作为输出变量历史值进行更新，接着利用输入变量历史真实值与输出变量预测值预测下一个输出变量值，直至预测完所有输出变量，即完成长期异常数据重构。如式(8)所示，实时更新预测后的输出变量，并代入下一次计算中。

Y(terror+k)=f[X(terror+(k-1)),…,X(terror+(k-1)-

n),…,Y(terror+(k-1)),…Y(terror+(k-1)-n)]

(8)

式中：terror为发生故障的时刻；k为后续故障时间序列，k=1,2，…，K；K为总的故障时间序列数。

同样选用后2天试验数据进行长期异常数据重构分析，图10与图11展示了后2天喷雾耙供气温度长期数据重构预测值与真实值的对比曲线。表3是长期预测情况下数据重构误差分析。由图10、图11与表3可知，长期预测相比于单步预测，预测值与真实值误差增加，曲线拟合程度降低。但预测值与真实值曲线拟合程度仍保持较好效果，说明训练好的动态神经网络对于长期的异常数据重构具有很好的泛化预测能力，可用于传感器损坏之后的长期异常数据重构。

表3 长期数据重构误差分析

图10 第7天供气温度长期数据重构

图11 第8天供气温度长期数据重构

4 结束语

文中构建了以喷雾耙入口温度、喷雾耙供气压力、风洞内部环境温度以及喷雾耙供气温度的历史延迟量作为输入和以喷雾耙供气温度作为输出的动态神经网络异常数据重构模型。通过构建的动态神经网络对前6天的结冰风洞喷雾耙供气温度异常的数据进行训练，将训练好的动态神经网络应用于后2天的喷雾耙供气温度数据重构，并与实际值作比较，得到以下结论：

(1)对于时间序列型动态神经网络的训练，并行排序的数据输入方式相比于序列排序的方式具有更小的均方误差及更好的线性相关度；

(2)对于单点异常的数据重构，采用单步预测，及时更新真实历史值，可实现较高的数据重构精度；

(3)对于长期异常的数据重构，可采用预测值实时更新历史值的方式进行长期预测，但因误差积累会导致预测精度下降，但仍具有较好的数据重构效果。