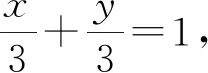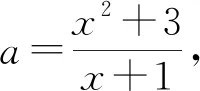例析方程有解求参数范围的几类问题
江苏省泰兴市实验初中教育集团 (225400) 陈 琦
在处理函数与方程的相关问题中,若方程有解则求参数的范围这类问题比较典型,最常用的解题方法有:分离参数、数形结合、分类讨论和等价转化等.下面举例介绍几个常见题型以及常用求解方案,供读者朋友参考.
一、一元二次方程在实数集上有解
如果是二次方程问题,使用判别式法是非常有效,如果是其他类型问题,参数分离法也比较多见.
例1 若方程(lgax)(lgax2)=-2所有解都大于零,求a的取值范围.
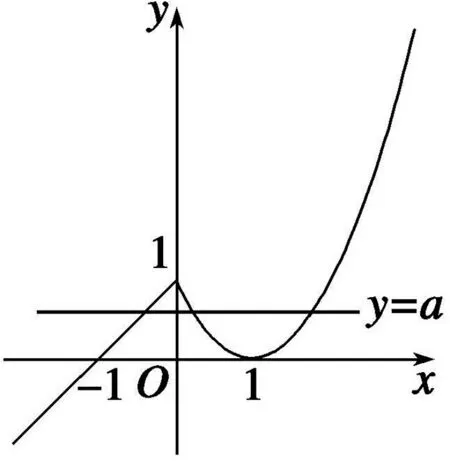
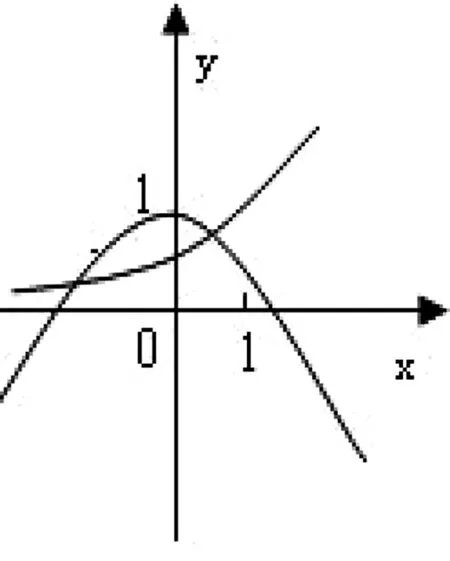
解析:先将方程化简得(lga+lgx)(lga+2lgx)=-2,即2lg2x+3lga·lgx+lg2a+2=0,设lgx=t,则有2t2+3tlga+lg2a+2=0(*) ,由于原方程有大于零的解,即x>0,故lgx=t∈R,即方程(*)有两个实解,所以△=9lg2a-8(lg2a+2)≥0,即lga≥4或lga≤-4,解得a≥1000或0 评注:本题虽然是一个对数问题,通过化简、换元可化归为一元二次函数有实数解问题,利用方程根的判别式可以迅速求解. 例2 若关于x的方程22x+2xa+a+1=0有实根,求实数a的取值范围. 评注:判断方程的根是否存在,可以通过构造相应的函数,将其转化为函数零点的存在性问题求解,也可直接通过分离参数,转化为函数的值域问题求解. 如果方程的解被限定在某个区间上,此时这个区间就是问题的主要条件,解题时必须给予充分考虑. 图1 例3 已知方程x2+2(m+3)x+2m-14=0的两个根都在区间(1,3)之外,求m的取值范围. 评注:由于方程f(x)=0的两根分布在区间(1,3)之外,即区间(1,3)必须是方程x1,x2(x1 例4 已知a是正实数,如果方程2ax2+2x-3-a=0在区间[-1,1]上有实根,求a的取值范围. 评注:由于此题中涉及的函数为二次函数,解题中抓住二次函数的特征(对称轴、顶点),并结合函数图像进行分析,通过建立相关的不等式(组)可使问题获得圆满解决. 如果方程所对应的函数是一个复合函数,探索此类方程的解的问题,多数是通过研究对应函数图像的有关交点情况解决. 图2 解析:设t=f(x),则方程为t2-at=0,解得t=0或t=a,即f(x)=0或f(x)=a,如图2,作出函数f(x)的图像,由函数图像可知f(x)的解有两个,故要使方程f2(x)-af(x)=0恰有5个不同的解,则方程f(x)=a的解必有三个,此时0 评注:此题是复合函数方程的问题,并且涉及的函数是分段函数,根据题目的特点与所求,对方程进行分解,并利用函数图像进行分析是解决参数范围最有效的途径. 图3 点评:虽然此题的复合函数方程与上题的形式不同,但通过换元并分层利用函数图象分析是解决此类问题比较有效的方法. 所谓的超越函数,就是非我们熟悉的代数函数,其方程我们是不能用普通的方法解决,画出对应函数图像进行分析是最基本的方法. 例7 已知方程2x-1+2x-a=0有两个根,求实数a的取值范围. 图4 评注:对于超越方程解的情况的判定,画函数图象是一个行之有效的方法,解题过程中要对特殊点的位置进行准确定位,还须正确分析函数图象的基本走向. 有关交点、函数零点问题都是方程有解问题的另一种表现形式,很多情况都可以转化为方程有解问题来解决. 例8 已知抛物线y=-x2+ax-1和点A(3,0),B(0,3),若抛物线与线段AB有两个不同的交点,求a的取值范围. 评析:此题根据线段与抛物线的位置关系,由两个方程的联立将原问题转化为函数的零点问题,这说明了函数的零点问题在解决其他问题中的关键作用,应引起足够的重视. 例9 已知函数f(x)=ex-1+x-2(e是自然对数的底数),g(x)=x2-ax-a+3,若存在实数x1,x2,使得f(x1)=g(x2)=0,且|x1-x2|≤1,求实数a的取值范围. 评注:本题从表面上来看不是方程有解问题,但通过分解问题并进行层层推理探索,就将其化归为此类题型了,解题中的分析推理,取得了“破茧抽丝”的效果.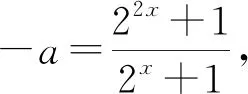
二、一元二次方程在某区间上有解
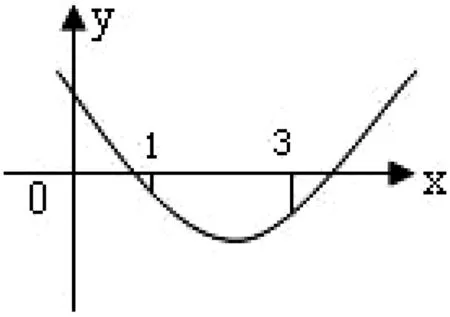
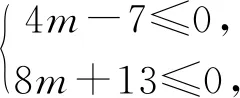
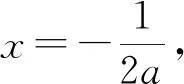
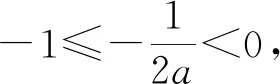
三、复合函数方程有解问题
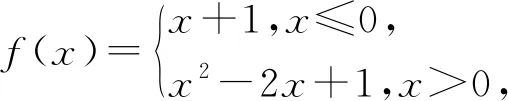
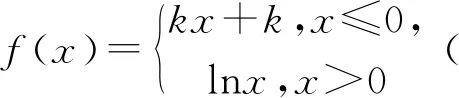
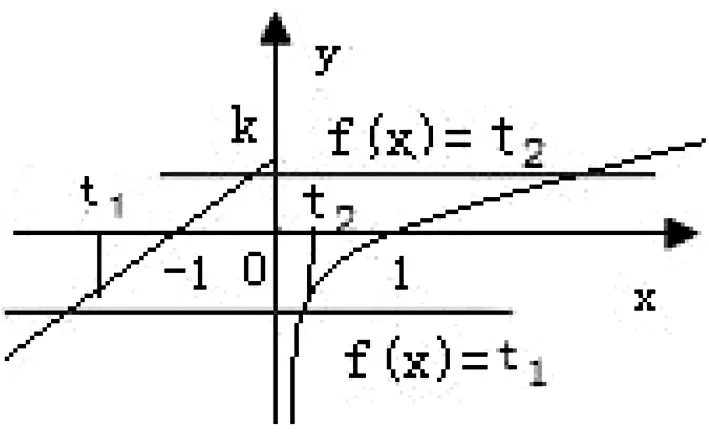
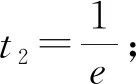
四、超越函数方程有解问题
五、可转化为方程有解的问题