构造圆方程求解弦对定点张直角的问题

江西省吉安市白鹭洲中学 (343000) 董永芳 刘忠浪

解析几何中的弦对定点张直角问题有很多解法，除了常规解法外还有齐次化、点乘双根法等方法，本文以2007年山东卷解几题为例,介绍求此问题的另一种构造圆方程方法，并将其推广为一般结论.

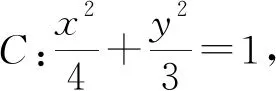
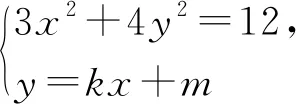
评析：以上方法相比于一般常规方法少了许多复杂运算，简便快捷.特别是解法中由①+②得到以AB为直径的圆的方程的运用并且可以得到以AB为直径的圆过椭圆上任意一点，则直线l必过定点的结论.

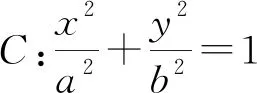
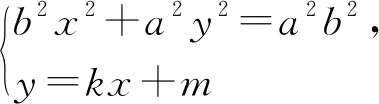
(2)当直线平行于坐标轴时，结论显然成立.

类似的，还可以将结论推广为：

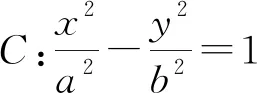
结论3 已知直线l与抛物线C:y2=2px相交于A,B两点，若以AB为直径的圆过抛物线上一点P(x0,y0)(异于点A,B)，则直线l过定点(2p+x0,-y0).

运用结论不难完成以下问题：

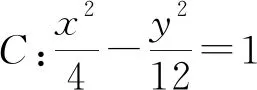
(答案：直线l过定点(-8，12)).

题2 已知直线l与抛物线C:y2=4x相交于A,B两点，若以AB为直径的圆过抛物线C上一点P(4,4)(异于点A,B)，证明：直线l过定点.

(答案：直线l过定点(8，-4)).