梯度策略的多目标GANs帕累托最优解算法

张 波，徐黎明，2，黄志伟，要小鹏

1.西南医科大学 医学信息与工程学院，四川 泸州646000

2.重庆邮电大学 计算机科学与技术学院，重庆400065

近年来，生成对抗网络（Generative Adversarial Nets，GANs）[1]在深度学习和图像处理领域取得了巨大的进展，与之前的深度生成模型[2-3]相比，GANs 具有强大的数据拟合和近似能力。它不仅消除了马尔可夫和可展开近似推理网络的约束，也为拟合各种数据提供了灵活的框架。GANs的概念和框架相对较新，但已成为一个热门的研究主题。正如LeCun 所说，GANs 是过去十年中机器学习领域最令人兴奋的想法。到目前为止，GANs 在Google 学术中的引用量已超过17 000 次。随着GANs理论的不断成熟以及与其他技术的融合，它被广泛地应用于包括图像复原[4-6]、图像超分辨率[7-9]、图像隐写术[10]、文本-图像合成[11]、图像-图像转换[12-13]、图像分类[14]和图像检索[15]等多个图像子领域。

在以生成对抗网络或者对抗训练为基础的图像模型中，其目标函数往往包含多个损失项，每项损失代表一个目标，旨在完成一种特定的任务，并且这些损失项之间往往存在相互“矛盾”甚至“竞争”的关系。求解这类非凸函数的全局最优解较难，大部分GANs模型不会直接寻求全局最优解，而是先利用交叉验证的方法确定最优权重参数，然后再利用梯度策略和线性搜索方法，沿着梯度下降的方向，搜索帕累托最优解。但这种方法存在2个明显的缺陷：

（1）当目标数量较多时，采用交叉验证方式确定权重参数的过程非常耗时，并且得到的权重参数不能保证对于整体参数求解是最优的。

（2）当目标数量较多或者参数梯度的维度较高时，线性搜索并不能直接应用到大规模学习任务。

根据文献[16]的总结，大部分面向应用的GANs 模型都包含多个损失函数，并且含有大量参数，梯度的维度较高，这给求解参数最优解带来了巨大挑战。对此，本文提出基于梯度策略的多目标生成对抗网络的帕累托最优解搜索算法。

1 相关工作

与多目标优化相关的是多任务学习，有文献[17]证明可以通过多目标优化来解决多任务学习，并简单认定在优化层面多任务学习等同于多目标优化。当给定多个任务或多个目标时，寻找帕累托最优解是一个多目标优化问题。在机器学习中，多目标优化可以归纳为，训练一个模型来执行多个任务，而多个任务之间可能存在相互“矛盾”的关系，多目标优化则能够优化一组可能冲突的目标或任务。常见的优化方法是选择优化代理目标，即，通过最小化多个损失的加权线性组合来进行优化。多目标优化或多任务学习可以通过建立归纳偏差，然后最小化单个任务经验风险的加权和来进行参数求解。

早期的多任务学习认定，对比独立地学习每个任务，使用来自多个任务的数据能够取得更好的性能[18]。多任务学习通常是通过参数共享进行的，在实际求解过程中，参数共享分为硬参数共享和软参数共享两种方式。硬参数共享方法中，一部分参数共享，另一部分参数依赖于特定的任务。采用软参数共享方法时，所有参数都基于特定任务，并且所有参数都被贝叶斯先验或联合词典约束。现阶段，基于梯度策略的多目标优化方法都是基于硬参数共享实现的，因此，本文重点关注这类方法。

Baxter等人[19]从理论上将多任务学习问题分解为个体学习者与元算法。每一个学习者要负责一项任务，元算法决定怎样更新共享参数，上述提到的优化代理目标就使用加权求和作为元算法。基于这种方式，后续有学者提出了许多改进方式。Li 等人[20]提出每个学习者都基于核学习来进行多目标优化。Zhou 等人[21]首先假设所有的任务共享一个词典，然后提出使用期望似然最大化的元算法来实现多目标优化。此外，Zhou等人[22]还提出了群体多目标优化策略。随着多目标优化问题研究日渐成熟，还有学者将多主体学习[23]，顺序决策[24]和贝叶斯优化[25]应用到多目标优化问题中。

此外，基于梯度策略的方法也被提出，并取得较好的结果。Fliege[26]和Désidéri 等人[27]利用Karush-Kuhn-Tucker（KKT）条件，找到所有目标经验风险的梯度下降方向，然后在此方向上进行线性搜索。由于硬件设备的不断发展，这种策略随后又被扩展到利用随机梯度更新，Poirion等人[28]与Chen等人[29]提出了基于不确定性随机梯度策略的方法用于多目标卷积神经网络的优化。

与本文所提算法最接近的是MGDA[27]算法和Frank-Wolfe[28]算法，二者都基于梯度策略进行线性搜索，但这两种算法适合目标数较少以及参数梯度维度较低的情况，并不能有效地处理目标数较多的情况。由于GANs包含多个深度神经网络，拥有巨量的参数，梯度维度较高。因此，MGDA 算法和Frank-Wolfe 算法不能直接适用于多目标GANs优化。基于这两种算法，本文所提算法将多目标优化问题分解为多个两目标优化问题，然后再沿着梯度下降的方向进行梯度更新和线性搜索。

2 本文工作

原始的生成对抗网络[1]优化采用梯度上升法优化判别器，同时采用梯度下降法优化生成器，后续许多GANs 改进模型都基于这类梯度策略。由于原始的GANs 中只有一项损失，即，用于拟合真实数据流形的对抗损失，这种梯度策略非常有效。但在面向任务的GANs 模型[16]中往往包含多种损失。如，图像复原任务中，包含重建损失、视觉感知损失等；图像-图像转换任务中，包含循环一致性损失，边缘保持损失等。不难证明，包含多个损失的目标函数是非凸的，可以将这个非凸函数总结为：

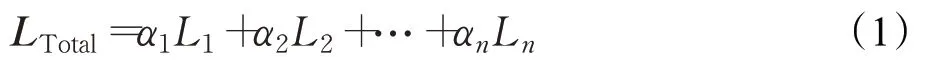
其中，L={L1,L2,…,Ln}表示不同的损失或者目标，α={α1,α2,…,αn}表示不同的权重参数。现阶段，基于梯度策略的多目标GANs 都采用硬参数共享方法来求解。因此，可以将GANs模型的参数θ 分为共享参数θs和特定参数θk。结合式（1），可以得出优化式为：

其中，K 表示目标数量。前文提到，可以将多任务学习看作是多目标优化问题，即，优化一组可能冲突或竞争的任务。因此，式（2）可以展开为：

求解式（1）和（3）这类包含巨量参数的非凸函数的全局最优解较难，是一个可证明的NP难问题。因此，大多数算法选择寻求帕累托最优解。

对于不同的目标数量，本文采取不同的求解方法。根据GANs 综述论文[16]，大体上将目标数分为K=1、K=2 和K ＞2 三种情况进行求解。在基本的图像合成任务中[1]，任务数K=1，不存在相互冲突的任务或目标。此时可以认定帕累托最优解即为模型的全局最优解，按照GANs提供的梯度策略方法进行求解即可。当任务数K ＞1 时，GANs 的结构多为深度编码-解码结构。对此，将编码器参数设置为共享参数，解码器参数设置为特定参数进行求解。

2.1 两目标帕累托最优解（K=2）

现在已经有一些基于梯度策略的方法能够有效搜索帕累托最优解。MGDA 就是一种典型的方法，该方法通过添加KKT（Karush-Kuhn-Tucker，KKT）条件到共享参数和特定参数上，进行求解。

文献[27]已经证明满足上述KKT 条件的任何解均为帕累托最优解，并且，帕累托最优解要么为0 且所得模型参数和权重参数满足KKT 条件，要么帕累托最优解位于参数梯度下降方向。因此，所得的多目标优化算法是针对任务特定参数的梯度下降，即，求解：

此时，搜索帕累托最优解比较容易，可以计算式（5）（二次方程）的最优权重参数为：

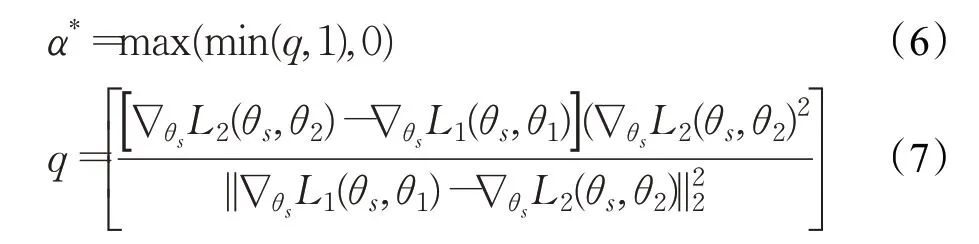
当确定最优权重参数后，可视化搜索帕累托最优解的过程，如图1所示。

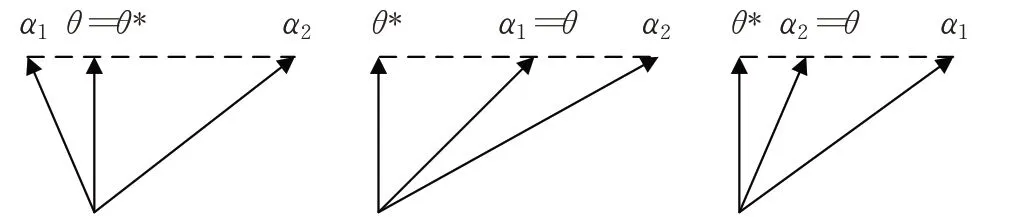
图1 K=2时，三种可能的帕累托最优解

根据以上分析，可以得出当K=2 时的搜索算法，如算法1所示。

算法1两目标帕累托最优解算法

图1 表明，当K=2 时，帕累托最优解的范围较小。因此，通过算法1能够有效地搜索出帕累托最优解。以CE 模型[4]和SRGAN 模型[7]为例，这两种模型只包含两种损失，采用式（6）确定的权重参数，与使用交叉验证的方式获得的权重参数，对GANs模型产生了相当的性能影响。但是算法1不需要繁琐的交叉验证，能够进一步缩短训练时间。

2.2 多目标帕累托最优解（K＞2）

K=1 或K=2 可以看作多目标GANs优化的特例，而K ＞2 是多目标GANs 优化的一般情况。当K ＞2时，采用常见的交叉验证方法确定权重参数非常耗时。随着目标数量的增加，验证过程的耗时情况几乎呈指数增长。同时目标数量的增加，目标之间的“冲突”情况更复杂；参数维度较高，直接应用线性搜索算法容易陷入局部最优。基于MGDA算法，所提算法将多目标GANs优化问题分解为多个两目标优化，确定最优权重参数之后，再沿着的方向使用线性搜索来获取帕累托最优解。具体如算法2所示。

算法2多目标帕累托最优解算法

此时，GANs 模型达到最优状态，各项损失不再变化，梯度不再更新。因此，α={α1,α2,…,αK}即为式（4）的最优权重参数，并且当前参数为该式的最优解。

其中，λ=1-ω 是常数，ω 表示固定权重参数的和。

综上所述，多目标GANs 优化取决于特定的目标数，当K=2 时，采用算法1进行优化求解；当K＞2 时，采用算法2进行优化求解。

3 实验结果

为了验证算法1 和算法2 在实际应用中的有效性，主要对比两种权重参数确定方式以及对图像任务的性能差异：

方式1利用交叉验证方法确定权重参数；

方式2利用算法1或算法2确定权重参数。

对比算法涉及图像修复，图像超分辨，图像-图像转换和图像哈希检索等多个领域。具体算法包括：CE[4]、SRGAN[7]、RankSRGAN[8]、BicycleGAN[12]、SNSR-GAN[13]和BGAN[15]。进行实验对比时，采用原文献提供的数据集和源代码，所提算法和所有对比算法的仿真实验建立在“四核Intel®Core™i-7685K CPU @3.6 GHz”处理器和四块“NVIDIA Titan V”的硬件环境上。

为了直观展示算法1 和算法2 的优势，选择PSNR和SSIM 收敛情况进行对比，所有模型重复训练500次。PSNR和SSIM的定义分别如下：

其中，M和N分别表示图像的大小，I(x,y)和I*(x,y)分别表示原始图像和变换图像。Max(I(x,y))表示原始图像中最大的像素值[30]。

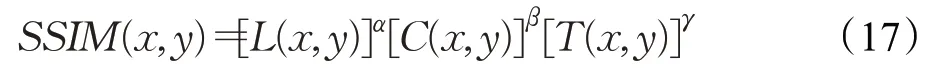
其中，L(x,y)表示亮度函数，C(x,y)表示对比度函数，T(x,y)表示结构函数。α、β和γ表示对应函数的权重[30]。

根据目标数（损失项数量），将从以下三方面讨论所提算法的有效性。

3.1 K=2

本节实验主要对比CE 模型[4]和SRGAN 模型[7]，这两种模型均包含两种损失函数，即，K=2。CE模型包含对抗损失和重建损失（L范数），SRGAN 模型包含对抗损失和内容损失。尽管内容损失还包括MSE 损失（Mean Square Error，MSE）和视觉感知损失，但二者权重相同，可以认定SRGAN 只包含两种损失。实验结果对比如图2、图3所示。

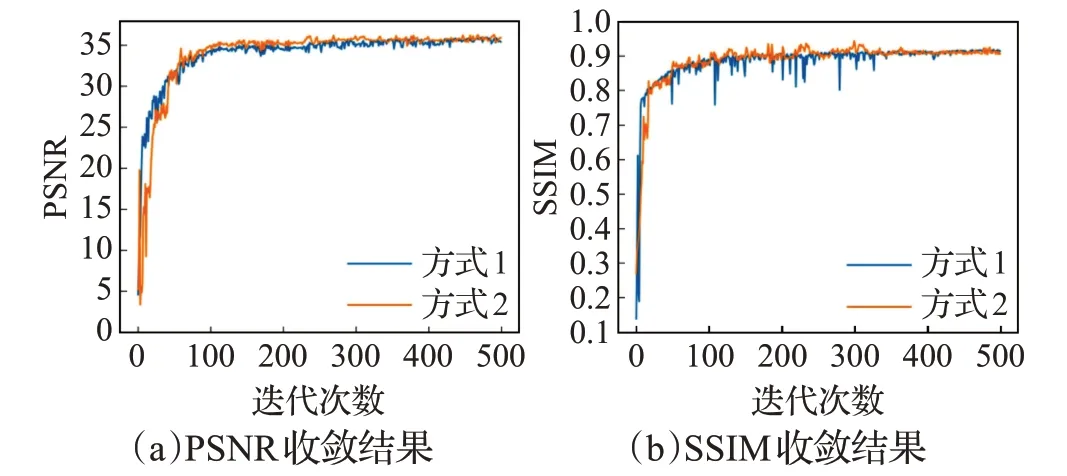
图2 方式1、方式2在CE模型上的性能对比

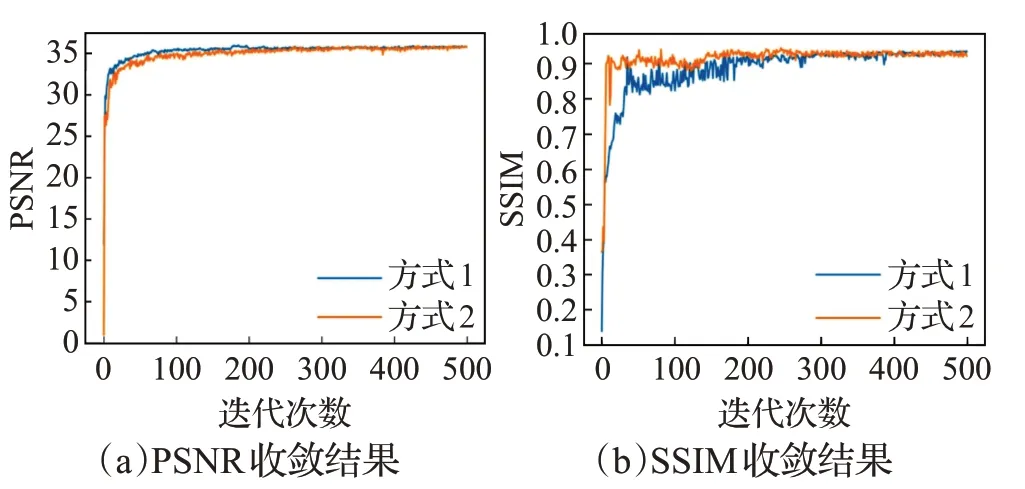
图3 方式1、方式2在SRGAN模型上的性能对比

图2、图3 显示，采用算法1 确定的权重参数与原文采用交叉验证方法确定的权重参数，对模型的整体性能影响相当，二者都能产生较好的实验效果。但是在实际训练过程中，算法1 耗时少，可操作性和参数自适应更强。

3.2 K＞2

本节实验主要对比RankSRGAN[8]、BicycleGAN[12]和BGAN[13]模型，这三种模型的目标数分别为：K=3、K=4 和K=5。如前文分析，由于目标数较多，采用交叉验证确定权重参数异常耗时。因此，实验直接采用原文中的权重参数和训练数据集。实验结果对比如图4～6所示。

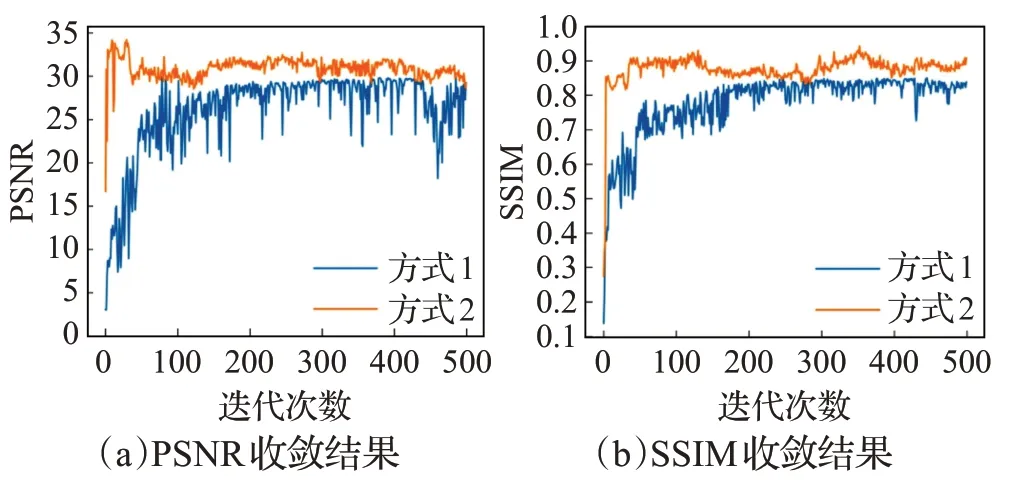
图4 方式1、方式2在RankSRGAN模型上的性能对比

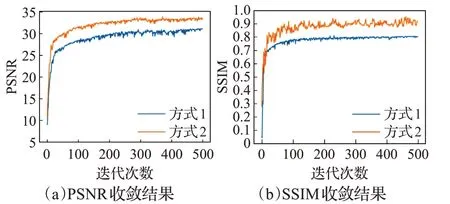
图5 方式1、方式2在BicycleGAN模型上的性能对比

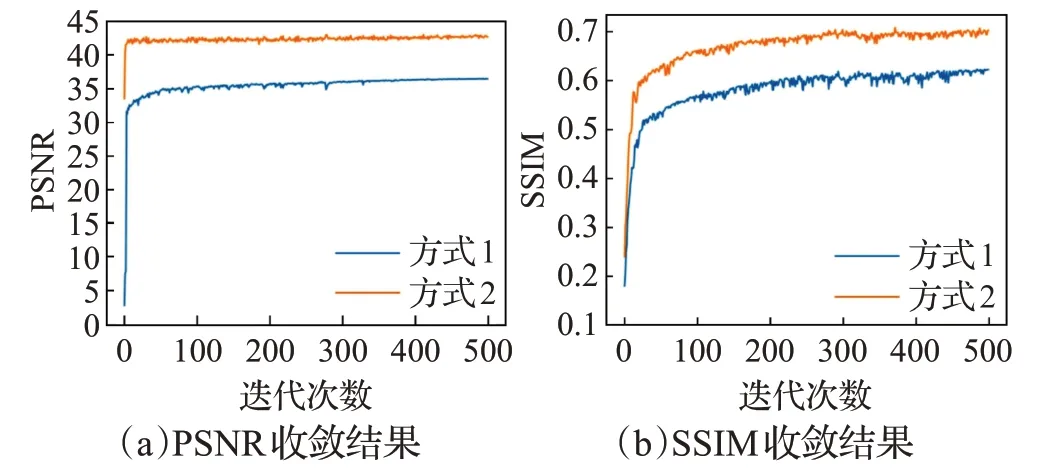
图6 方式1、方式2在BGAN模型上的性能对比

图4～6 显示，当K＞2 时，对比交叉验证，算法2 具有明显的优势，并且目标数量越多，产生的优势越明显。此外，结合图2～6 可以看出，采用方式1 训练的模型，获得的PSNR或SSIM值收敛性较差，这间接地说明了采用方式1确定权重参数并非最优权重，同时也说明了对于权重参数敏感的模型而言，非最优权重参数对模型的性能影响较大。

3.3 K＞2但部分权重参数固定

本节实验选择SNSR-GAN 模型[13]进行验证。该模型包含6种目标，但为保证病理不变性和保持医学图像的边缘信息，根据先验知识，设置了其中3个权重参数，即，该模型中的部分权重参数是确定的。此时，需要将算法2中的步骤8替换为式（15）。实验对比结果如图7所示。图7显示，对于多目标优化任务并且部分权重参数确定的情况，所提算法仍能产生较好的实验结果。

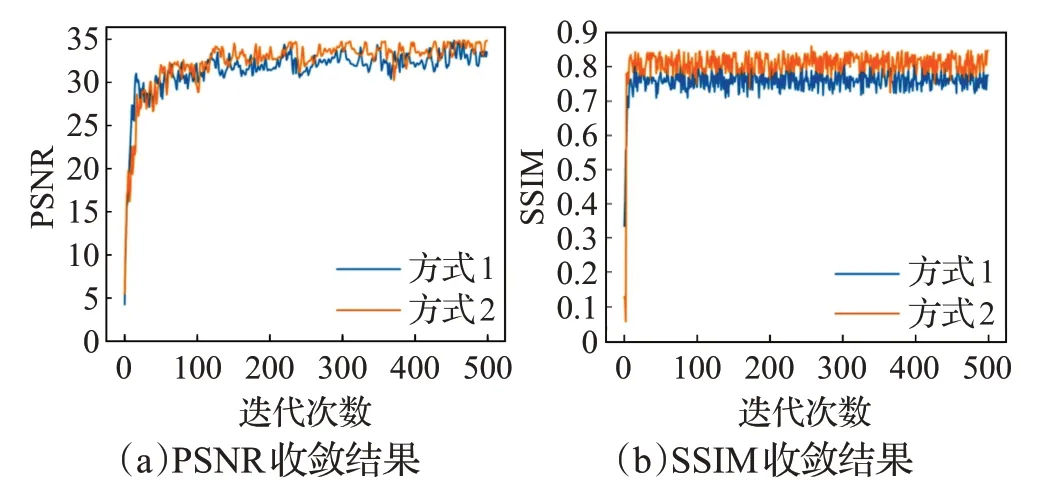
图7 方式1、方式2在SNSR-GAN模型上的性能对比

为比较所提算法与交叉验证方法的计算耗时情况，本文根据文献[4，7-8，12-13，15]提供的源码，估计获取最优参数的时间。结果如表1所示。

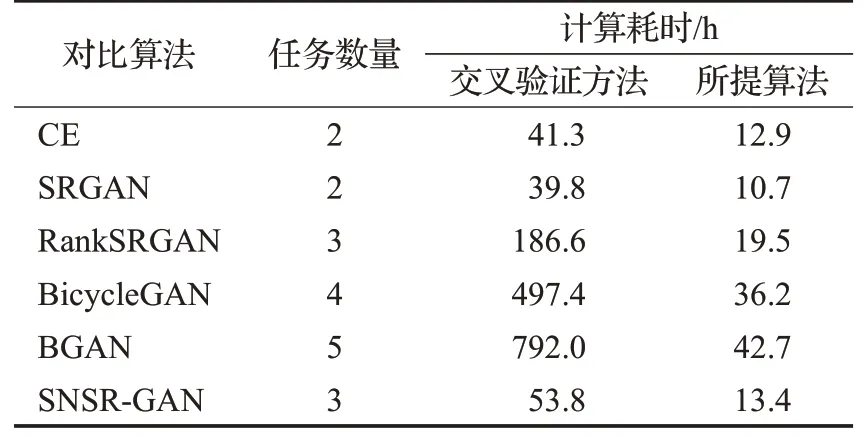
表1 交叉验证与所提算法计算耗时对比

结合图2～7 和表1 的实验结果可以看出，当不确定权重参数的数量等于2 时，方式1 和方式2 产生相当的实验结果，但所提算法可操作性和参数自适应性更强，耗时更少；当不确定权重参数的数量大于2 时，本文所提算法能够产生更好的实验结果，同时耗时少，可操作性、自适应性强。

4 结束语

为了优化多目标生成对抗网络及求得帕累托最优解，本文基于梯度策略，将多目标优化分解为多个两目标优化，提出帕累托最优解求解算法，较好地解决了求解多目标、高维度生成对抗网络最优解的NP 难问题。此外，将所提算法应用到多个图像子领域，实验结果进一步验证了所提算法的有效性。实验结果显示，即使部分参数权重确定，只要模型的待确定参数权重大于2，所提算法具有明显的性能和计算优势。在训练和更新深度神经网络时，由于梯度反向计算和更新比前向计算更耗时，导致整个算法比其他基于梯度策略的方法耗时。算法的耗时仍是文章值得改进的地方，这也是下一步的研究重点。