高速弯沉仪检测技术研究进展

徐艳玲，唐伯明，朱洪洲，王俊新

(重庆交通大学 土木工程学院,重庆 400074)

0 引言

随着我国公路建设的飞速发展，已建成的公路里程不断增加，截至2019年，中国公路总里程已达484.65万km、高速公路达14.26万km,居世界第一。我国未来公路的发展趋势以养护修复为主，随着无损检测技术的广泛应用，路表弯沉测试对于路面结构性能评价日趋重要，路面弯沉数据不但用于评价既有路面的结构状况，还可用于辅助路面结构加铺层设计、评估路面响应的季节性变化、评估工程的结构变异性、表征加铺层材料特性参数与路基承载能力等；对于刚性路面，弯沉测试还可用于确定接缝和裂缝的传载能力以及探测路表下的空洞等路面病害检测。路面行为特性的评价与预估可大大节约养护维修成本，所以关于弯沉测试方法及理论在国内外得到广泛的应用与研究。

目前国外用于确定弯沉形状及路面结构层特性的无损检测技术主要有以下6种：落锤式弯沉仪法(FWD)、滚动动力弯沉仪法(RDD)、滚轮式弯沉仪法(RWD)、机场滚轮式弯沉仪法(ARWD)，道路弯沉仪法(RDT)、高速弯沉仪法(HSD)。其中FWD理论体系较为完善，FWD弯沉数据的分析与应用较为成熟，具有国际公认性，而其他5种设备尚处于不同的研究阶段。国内的无损检测技术主要有以下4种：贝克曼梁法(BB)、自动弯沉仪法、落锤式弯沉仪法(FWD)、激光式高速路面弯沉仪法。而这4种方法中，传统贝克曼梁法将随着技术的发展逐渐被淘汰，FWD是国内目前道路验收以及路面结构评定的主要方法，而激光高速路面弯沉仪法是《公路路基路面现场测试规程》(JTG3450—2019)中新增入的测试方法，但其理论与应用仍处于初级水平。

FWD作为无损检测中最主要的检测技术，能够有效地测量荷载板下的弯沉值用于确定路面的刚度及其他特性，但是也有明显的缺陷,就是测试的间断性，在测试时需要进行交通管制，测试效率低。而高速激光弯沉仪的出现弥补了这些缺陷，以明显的优势成为未来检测技术发展新方向。这种技术发展的潜在优势有[1]：(1)相对于现有的随机选点测试弯沉值(如FWD)而言，这种高速弯沉测试系统能够连续测试路面的弯沉数据；(2)高速弯沉测试系统可以减少用户的延误时间成本，也可以避免交通安全问题，比如传统的弯沉测试需要进行交通管制时容易产生交通安全事故，高速弯沉测试仪以正常的交通流进行测试，不会影响其他车辆的运行。(3)路面管养单位可以利用这个系统获取路面的实时状况，以便做出最佳养护决策，从而达到路面最长的使用寿命、最少的养护成本以及最小的延误成本。(4)路面建设单位在施工过程中可以利用该系统对路面结构的薄弱环节进行定位、修补以及消除路面结构薄弱点，最终保证施工质量，降低寿命周期成本，延长使用寿命。(5)通过GPS实时获取弯沉测量数据与GIS数据库联系起来可以形成地图信息，这些信息显示路面结构的薄弱点、混凝土路面传荷率低以及加铺层易受反射裂缝影响的位置。(6)可对未来2～3年要发生的路面病害进行预警，以便进行合理的路面养护和修复管理。

1 高速弯沉仪原型理论研究

自20世纪80年代以来，全球很多公路机构已开始使用FWD进行柔性路面以及混凝土路面结构的评估，而自1991年弯沉仪取消应用后，丹麦公路研究院一直致力于寻找一种不同于FWD的方法对全国公路网的路面结构状况进行初步筛查，而后在20世纪90年代中期立项研制一种新型高速弯沉仪，项目的主要团队是丹麦公路研究院和Greenwood工程公司,而荷兰代尔夫特理工大学和丹麦科技大学做主要合作者从事理论工作[1]。TSD(traffic speed deflectometer)最原始的两个原型由丹麦的格林伍德工程开发，且其版本也在不断的更新与完善之中，目前国内外高速弯沉的研究与应用基本都是基于丹麦的TSD原型技术，比如国内武大卓越首研发的激光动态弯沉测试系统Laser Dynamic Deflectometer(LDD)。TSD基于多普勒效应的激光速度传感器测量路面弯沉变形速度，小角度安装的激光器测量车辆水平速度、竖向速度、暂停速度及竖向路面变形速度。为了消除对于速度的依赖性，路面变形速度与车辆水平瞬时测量速度的比值表示为路面测试弯沉的斜率，弯沉速率以μm/s计，车辆速度以m/s计，弯沉斜率则以μm/s[2]计。轮载作用下路面变形速度矢量示意图如图1所示。由于弯沉比弯沉斜率能更直观反映路面结构承载能力，国内外路面结构状况的评价以及在路面管理系统的应用中大多采用弯沉值指标，所以如何利用激光器采集的变形速度确定现场路面弯沉值成了重点关注问题，且弯沉计算理论的完善直接影响到设备的研发及应用。本研究对高速激光弯沉检测技术的理论模型及分析方法进行了归纳总结，弯沉计算方法可归纳为两大类：(1)基于力学理论计算法；(2)曲线面积积分法。

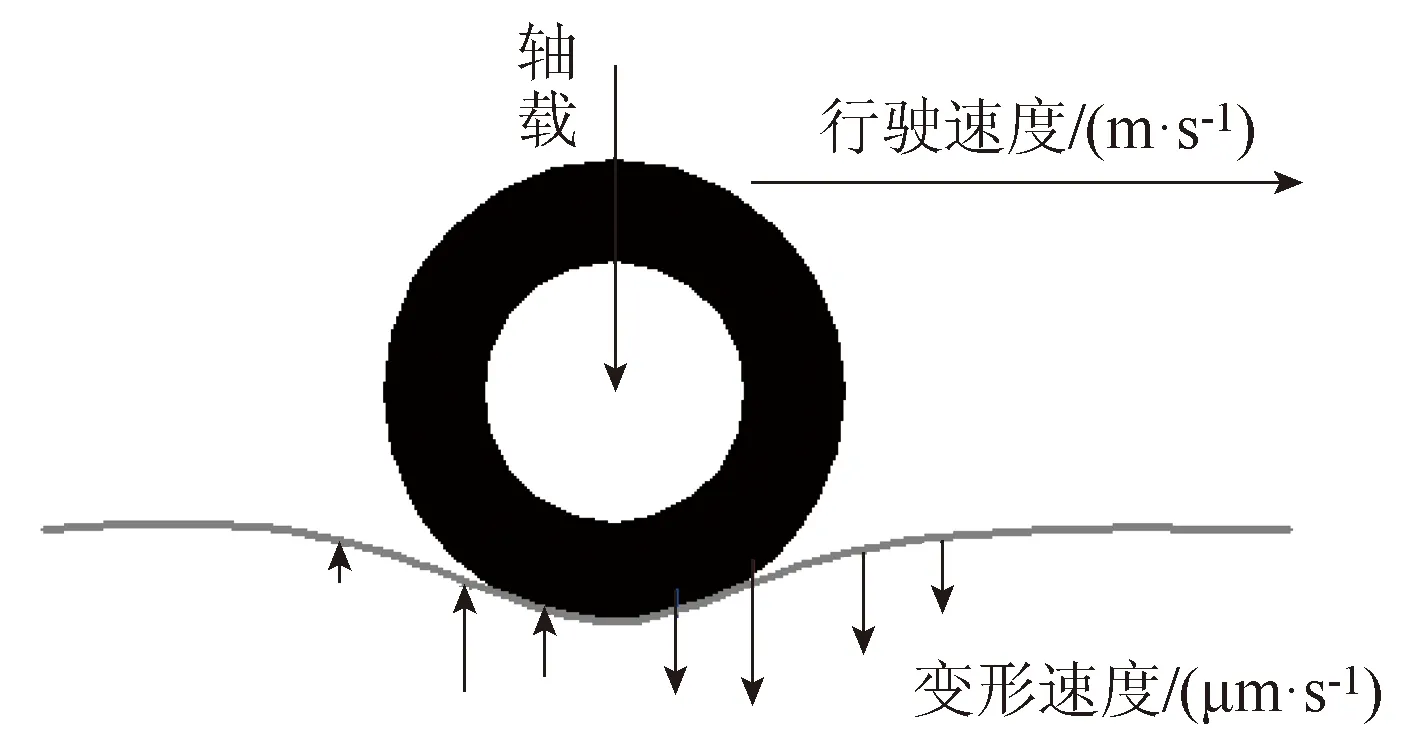
图1 滚动荷载作用下路面变形速度示意图Fig.1 Schematic diagram of pavement deflection velocity under a rolling load

1.1 基于力学理论计算法

基于高速弯沉仪测试的变形速度获取路面弯沉值，国外学者在理论上做了大量的研究。Kenneth[3]等首次提出了一种新的无损检测方法(高速弯沉仪法)测试路面结构承载能力，报告中采用多项式拟合路面变形速度的方法，然后通过拟合曲线积分得到弯沉值，具体拟合曲线实例见图2。

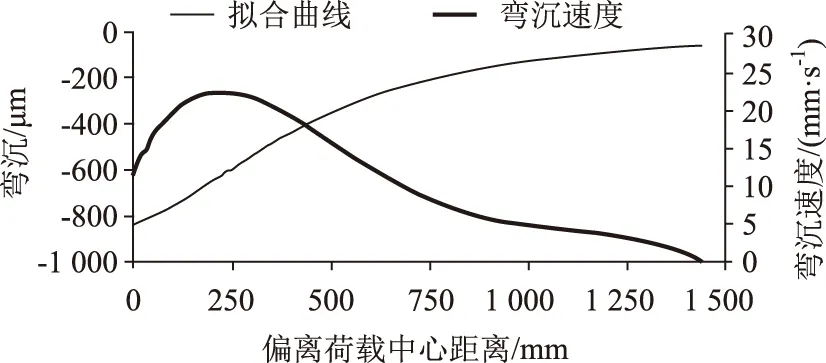
图2 20 m/s行车速度下弯沉速度及拟合曲线Fig.2 Deflection velocity and fitting curve at 20 m/s driving speed

Rasmussen[4]等以及国内的张德津[5]等采用Euler-Bernoulli梁理论和Winkler地基模型建模，路面受力简化后的弹性模型如图3所示，欧拉-伯努利方程表示为式(1),推导的曲线方程可表示为式(2)。但是Rasmussen在文中提到只有荷载作用位置附近的测点计算结果才可靠。

(1)

(2)

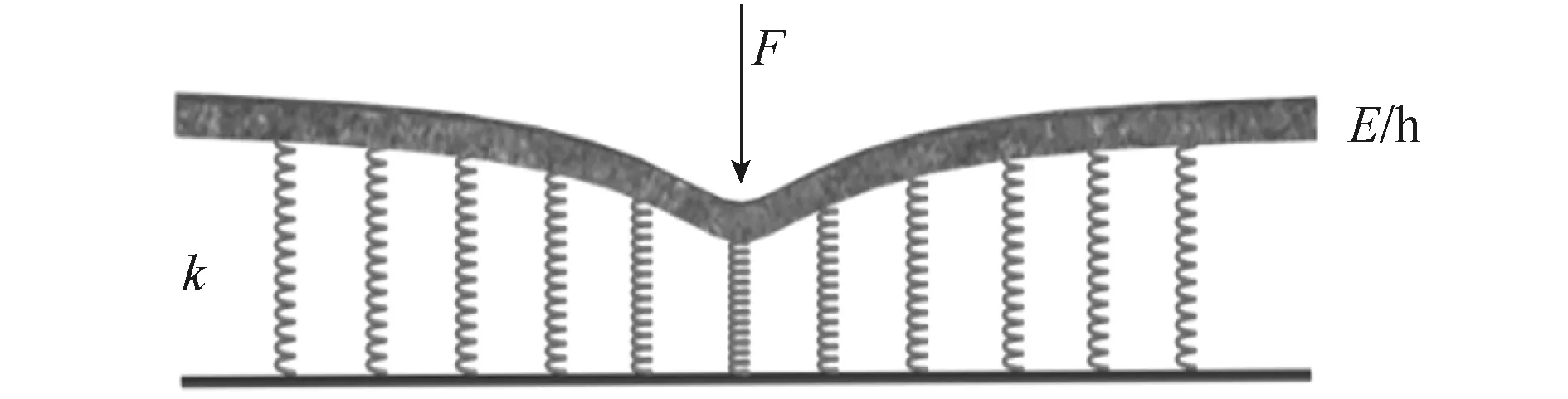
图3 弹性梁作用在线弹簧地基上的受力图Fig.3 Illustration of elastic beam acting on linear spring foundation

传统的梁/板模型计算的弯沉斜率与TSD实际测量的斜率比较时存在较大差异，Pedersen[6]等在greenwood公司的TSD弯沉算法基础上，对弯沉算法进行了进一步研究。根据2012年版TSD进行理论分析研究，路面结构假设为4层，如图4所示，基于连续介质力学的研究框架，对路面弯沉进行黏弹性模拟分析，弯沉斜率模拟为对称(高斯分布)与非对称(稳定分布)综合方程以及拟合弯沉曲线方程见式(3)～(12)，这些模型参数通过实测TSD弯沉斜率确定。

图4 层状路面结构示意图Fig.4 Schematic diagram of layered pavement structure

rSg1′(rxx,α,β,c,μ)+rNg2′(rxx,μ1,σ)，

(3)

g(rxx,α,β,c,μ,x,μ1,σ,rx,rS,rN):=

(4)

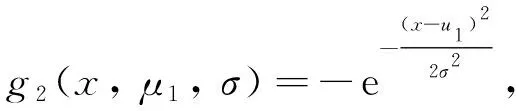
(5)

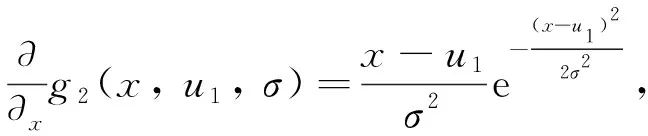
(6)

g1(x;α,β,c,u):=-f(-x;α,β,c,u),

(7)

φ(k;α,β,c,u)=eiku-|ck|α[1-iβsgn(k)φ(α, k)],

α=[0, 2],β∈[-1, 1],c∈[0, ∞],d∈R,

(8)

(9)

稳态分布f见式(10)：

(10)

f用于模拟弯沉，f的导数模拟弯沉斜率。方程(10)导数可以通过傅里叶转换为式(11)

(11)

或方程(10)的近似解为有限差分商

(12)

式中，α为特征指数，控制随机过程中的脉冲程度，值越小，脉冲越长，其尾部也越长，意味着远离中心位置的随机变量概率越大；β为对称参数，决定分布的倾斜度；c为控制参数，控制稳定分布的宽度；u为稳定分布的位置参数；rx为右侧x轴范围的尺度参数；rN为正态分布尺度参数；σ为高斯方程的变量，一般跟荷载的宽度有关，是一个固定值；u1为正态分布的位置参数，在稳定分布模式中是固定值；rs为稳定分布尺度参数。

为得到更准确的解析解，避免传统方法对模型的过于简化，Graczyk[7]等提出一种新的解析方法，将伽辽金法用于控制欧拉-伯努利梁变形的传统微分方程，基于单层路面体系分析路面弯沉，将路面模拟成由无限深黏弹性路基支撑的欧拉-伯努利梁，而实际作用的载荷以一组恒定速度运动的集中力来表示，见图5,图中欧拉-伯努利梁变形的经典运动方程见式(13)，推导的曲线方程见式(14)。

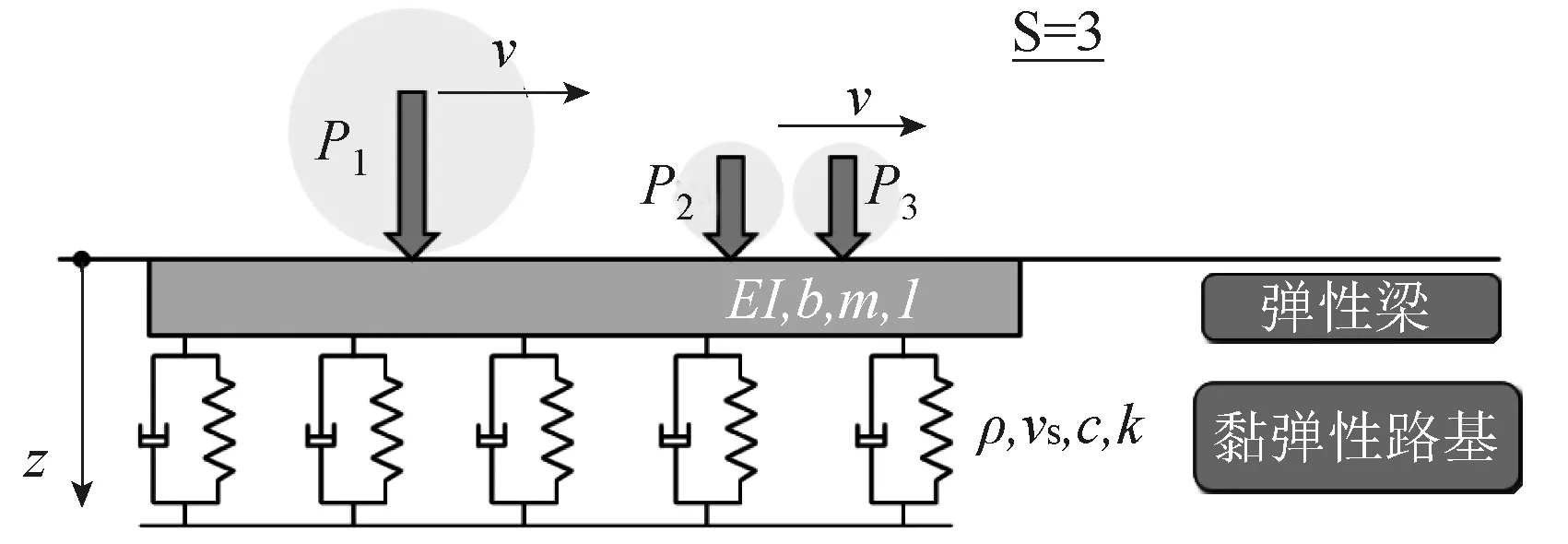
图5 移动荷载作用在无限厚度黏弹性地基支撑的弹性梁(欧拉-伯努利梁)上的结构Fig.5 Structure of moving load acting on elastic beam (Euler-Bernoulli beam) supported by infinite-depth viscoelastic subgrade

(13)

(14)

式中，z(x,t)为梁的竖向变形；EI为梁的等截面弯曲刚度；m为梁的单位截面质量；c为bρvs地基阻尼，b为基层宽度，β为地基密度，vs为地基压缩波速度；k为地基弹簧刚度；PS1为集中力；xs为荷载作用初始位置；v为荷载水平速度;S为集中力数量；δ(·)为狄拉克函数作为作用力位置方程函数。

Deng Y[1]认为在荷载作用下的路面响应如图6所示，延迟角φ反映了路面结构材料的黏弹性以及荷载的动态效应，在荷载作用下的弯沉盆是非对称的。为了模拟TSD测试条件以及有限元模拟计算的非对称弯沉盆，采用了Gumbel概率密度曲线进行拟合，如式(15)，此路面结构响应模型为路面结构材料的黏弹性、结构层的非线性以及荷载的动态模拟分析提供了理论基础。

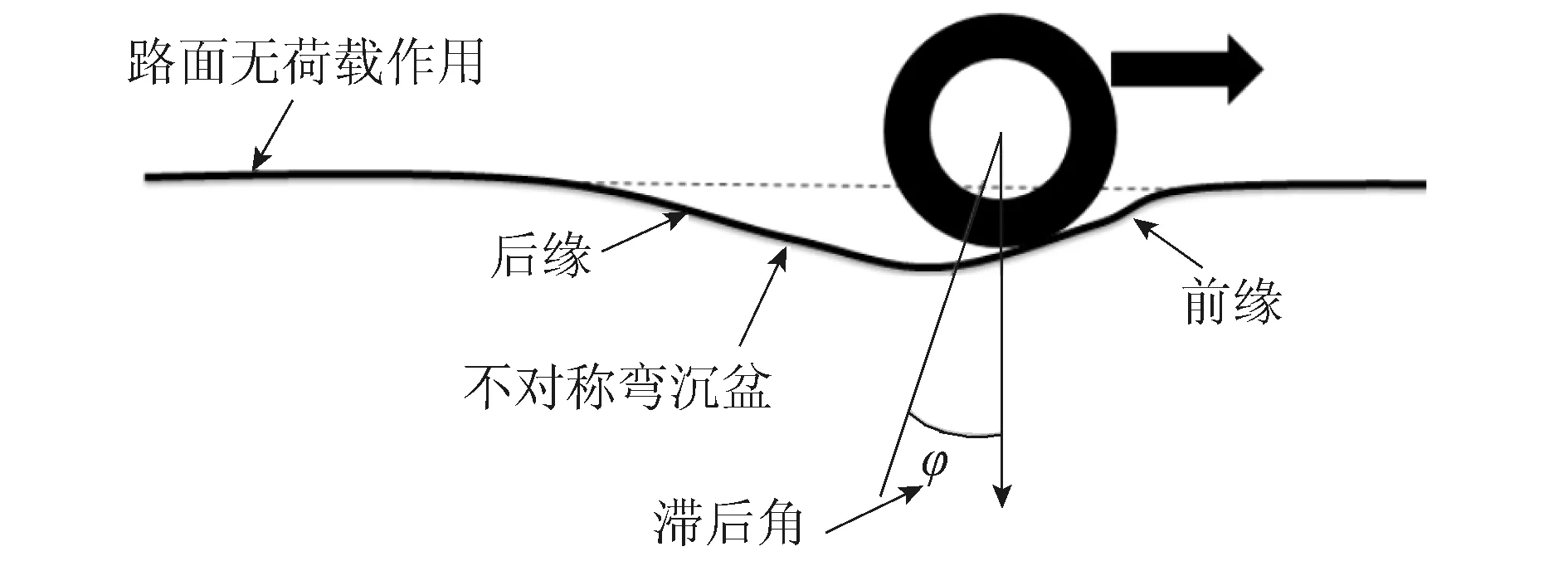
图6 移动荷载作用下非对称弯沉盆示意图Fig.6 Schematic diagram of asymmetric deflection basin under moving load

(15)

式中，W(x)为Gumbel概率密度曲线；x为测试距离，离参考点的距离；W0，ρ，β为模型参数。

1.2 曲线面积积分法

Muller[8]等通过TSD数据分析得到了不同的曲线段组合来模拟弯沉斜率曲线，计算曲线下的面积即弯沉值，弯沉盆形状通过从一参照点或者弯沉盆最边缘点的积分得到，利用的数值分析方法比较简单，具体计算式见式(16)～(19)，这个方法最大的优点是解决了离荷载作用位置较远处弯沉值计算结果不可靠的问题，得到荷载轴后面的弯沉盆形状，提高了测点最大弯沉值的准确度。

(16)

dx=VHdt,

(17)

(18)

(19)

将螺栓完全拧紧（指采用采用转角法拧紧螺栓时，拧紧螺栓的装配的扭矩达到上限，螺栓不再产生转角）[19-20]，并给电机通电，上位机测得曲线与相位差如图8所示，两曲线严格同步，所得相位差均小于0.1π，较为稳定。判定所得系统状态为正常工作，符合实验条件。

图7 通过VV/VH的描绘线下的面积计算路面变形轮廓线Fig.7 Deflected pavement profile calculated as the area under the plot of VV/VH

后续Zofka[9]等人提出了另一种处理TSD测试数据的计算方法，这种算法与欧拉方法描述类似，简称欧拉法，如图8，是除拉格朗日法外的另一种替换方法，其重点是离散点(i)沿着TSD测试路线分布,每个离散点的弯沉时程是时间函数(t)，即δi=f(t)，见图9。而利用韦布尔函数(Weibull)来拟合弯沉斜率，见式(20)，通过函数曲线与TSD荷载轴的距离积分来计算弯沉。

(20)

式中，k为形状参数；λ为尺度参数；u为位置参数。

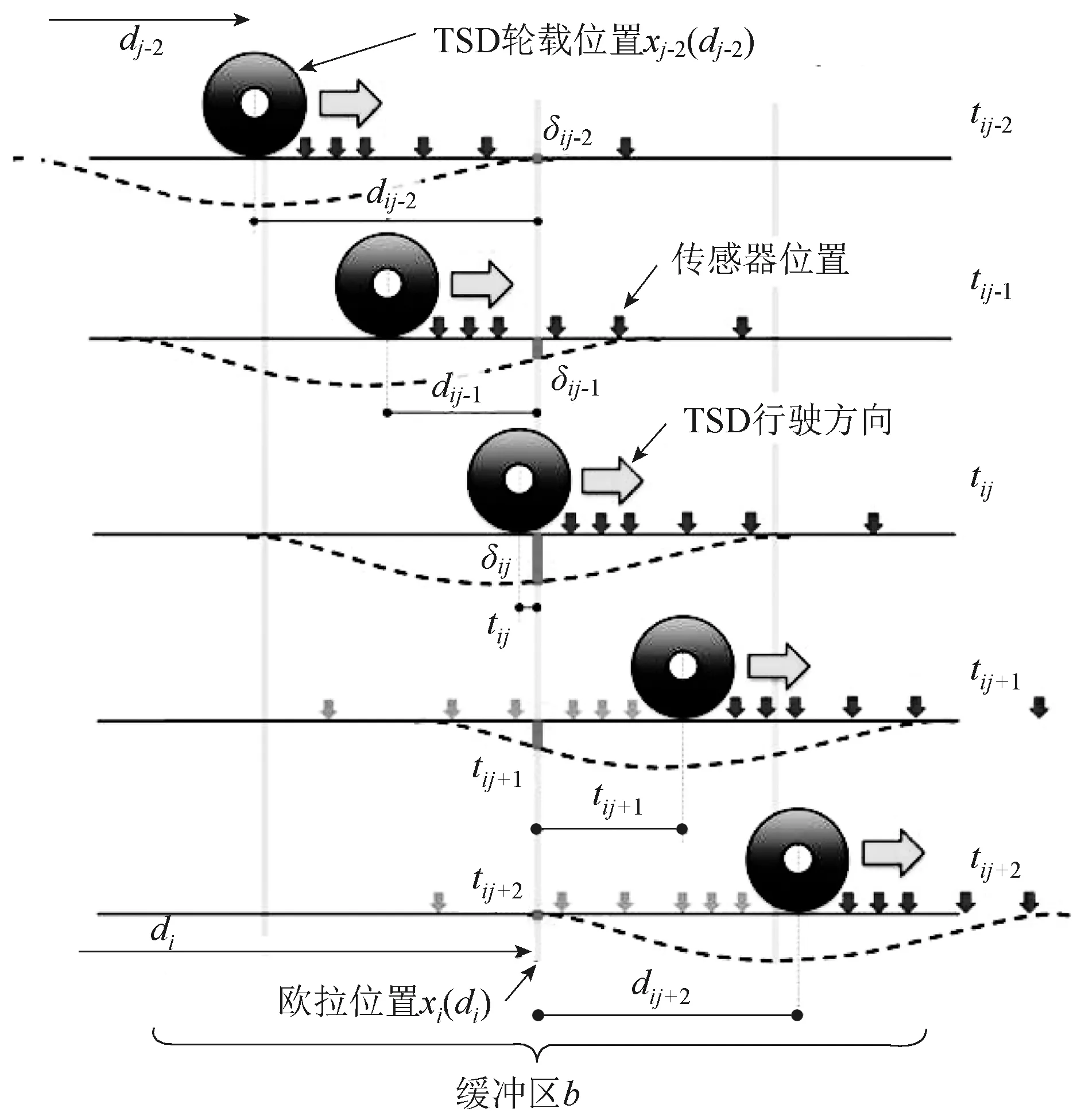
图8 欧拉方法概念图Fig.8 Eulerian approach concept diagram

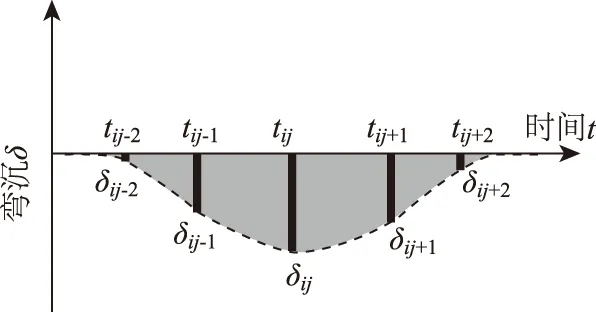
图9 TSD不同作用位置时欧拉离散点弯沉时程Fig.9 Deflection history of Euler discrete point at different TSD positions

利用韦布尔函数(Weibull)拟合弯沉斜率，通过求解函数曲线下的面积计算各点弯沉值，弯沉斜率函数如下式(21)。

(21)

式中，k为形状参数；λ为尺度参数

对国内外路面计算模型以及利用高速激光弯沉测试值计算路面弯沉的方法进行了详细的阐述，基于力学理论计算方面，为了使计算理论更准确，更符合现场路面结构响应，计算理论在不断完善，从简单的线弹性简化模型逐渐过渡到考虑移动荷载、黏弹性等因素的复杂模型。为了避免理论假设，演变出了曲线面积积分法，利用测试数据分析直接计算弯沉值。理论的不断更新完善为后续高速激光弯沉检测结果的分析与应用奠定了良好的基础，就TSD测试数据进行路面结构模量反算而言，合理的路面结构模型直接影响到反演方法的适用性和精度。目前国内对于高速弯沉仪理论方面的研究十分欠缺，应借鉴国外已有基础开展研究，提出适合国内路面结构体系的计算模型与方法，这对于高速弯沉仪国产化设备的完善与工程应用具有重要的推动作用。

2 高速弯沉仪测试精确度影响因素分析

高速弯沉仪在应用中，速度的提升往往会造成精度上一定程度的损失，所以在选用高速弯沉仪设备时，如何保证测试设备的精确度与可靠性是至关重要的问题，设备的精确度一般取决于下列几个因素：外部变量影响、平均值单元路段长度的选择、短期的重复性、与其他弯沉设备测量值的转换。

2.1 外部变量影响

在早期工作中,Hildebrand[10]和Kenneth[3]等根据当时激光器的精确度εvelocity为0.14 mm/s，测试系统1.5 m内安装了5个激光器，在正常的车辆速度(Vk=70 km/h(≈20 m/s))状态下的系统测试精度为4.7 μm/m，计算如下式(21)～(23)，从这个结果来看，激光器个数越多，系统测试精度越高。

(22)

(23)

(24)

在早期Flintsch[11]等人通过研究发现TSD测试时，噪音对测试结果有明显的影响。Levenberg[12]等通过统计学分析TSD和FWD的测量数据库，提出了一种新的比较方法，且基于TSD300指标利用泰勒图直接表示二者的关系，也可用来评估TSD设备的精确度。Katicha[13]等对噪音的变异性(噪音标准差)进行分析研究，认为TSD测量的噪声标准偏差的评估是确定测量精度的关键，因为只有排除了噪音的影响，才能得到路面结构测试值的“真值”，通过差分序列法求解噪音标准差以及路面“真值”标准差，而广义交叉试验法与平衡风险估算法对TSD测量值进行分析，发现风险平衡指标能更好地得到测试“真值”。Liao[14]等基于激光动态弯沉测试系统Laser Dynamic Deflectometer(LDD)分析了路面温度、车速、路面条件等因素对弯沉测试的影响，利用回归分析方法建立了动态激光弯沉仪(LDD)的测试弯沉环境参数修正模型，并通过多次实际工程验证了该校正模型在不同测量条件下的可靠性。通过与不同类型弯沉仪进行比较试验，验证了该校正模型在不同测量条件下的准确性。结果表明，该路面挠度连续测量修正模型在不同环境条件下具有较强的稳健性。Nasimifar[15]等基于动态-黏弹性分析了426种路面在TSD移动荷载下的动态响应，根据三维动态响应数据集值建立了SCITSD-Ref温度修正模型，该模型包括沥青路面层、温度以及结合料类型等敏感性参数，在美国的明尼苏达州试验路、维吉尼亚州、伊利诺斯州以及欧洲、澳大利亚进行实体路面验证，根据实体工程数据对模型进行了相应的调整。但是这些模型是基于模拟数据以及初步的实体工程验证分析，在全面实施之前还需要更多的实体工程来充分验证，因不同路面结构及不同气候条件下，修正模型会有差异。

2.2 平均值单元路段长度的选择及短期重复性

Flintsch[11]对单元长度0.1，1，10，100 m的弯沉斜率平均值分析发现100 m的平均值不能很好反映路面状况，所以在英国TSD采集的数据每1 m进行记录储存，而在出检测报告时用的数据是每10 m的平均值，TSD测试的短期重复性良好。美国联邦公路管理局(FHWA)基于TSD高速激光弯沉测试的现场试验立项了一个联合基金研究项目，加利福尼亚、乔治亚州、爱达荷州等9个州的交通局参与该项目，而Shrestha[16]等利用这9个州大约9 540 km的TSD测试数据进行分析，发现TSD测试具有良好的短期重复性以及长期的再现性。

2.3 高速弯沉仪法与其他测试法指标的转换性研究

由于FWD是目前国外路面结构状况无损检测的主要方法，是AASHTO设计指南以及MEPDG设计指南中通常推荐使用的弯沉测试设备,在国外FWD的应用、理论模型以及测试数据的分析较成熟，用于模量反演程序就有BAKFAA，DIADEF，BOUSDEF，CHEVDE，MODULUS，WESDEF等20多种，故一般都是高速弯沉仪与FWD测试数据进行对比分析。Flintsch[11]等人通过TSD测试弯沉斜率与FWD测试弯沉值进行了比较，发现二者数据具有一致性。Shrestha[16]等利用9个州大约9 540 km的测试数据进行对比分析，发现TSD与FWD二者测试的弯沉值具有一致性，对于FWD测试识别的需要加强路面结构承载能力部分同样能被TSD识别。Katicha[17]及Elseifi[18]等通过对比研究发现两种设备测试数据具有一致性，都能成功反映出测试路段的路面结构状况。但是上述研究中反映TSD测试并未对具体弯沉指标之间关系建立相关关系式。

一些学者对测试弯沉指标进行了进一步的研究，Roberts[19]等在澳大利亚和新西兰地区开展了丹麦的TSD与FWD弯沉测试值之间的关系研究，结果表明TSD和FWD最大弯沉测量值D0之间存在很强的线性相关性，但是不同地区关系式不同。Mano-haran[20]等利用TSD实测弯沉数据研究粒料基层柔性路面的结构性能，同样发现TSD及FWD最大弯沉D0之间具有良好的线性关系。Simonin[21]等在法国北部地区选用3种不同的道路(高速公路、主干道、次干道)进行了TSD试验以及FWD试验，发现TSD测试具有良好的重复性，弯沉斜率对于路面结构承载能力很敏感，利用高速公路、主干道、次干道3种道路的HSD测量值(弯沉斜率)与FWD弯沉测试值进行线性回归，能够得到良好的线性关系式，回归系数达到0.86，但是由于高速公路的回归点全部位于回归线以上，而主干路的回归点均位于回归线以下，故研究中说明不建议利用这种线性回归法将TSD测试弯沉斜率转换为弯沉值，但是HSD能够检测出道路承载力的状况以及反应有明显变异部分。Katicha[22]等发现简单的线性回归方法在分析设备的可重复性以及两种测试设备测量值之间的关系时会出现错误的结果，所以采用统计学中的一致性界限法(LOA)来评价TSD与FWD两种设备，二者测试值均转换成路表曲率指数(SCI)以及基层损坏指数(BDI)之后进行分析，结果表明利用LOA进行比较是非常有效的，尽管两种设备测量值计算的SCI和BDI之间的关系非常接近线性，但是关系中存在明显的变异性和偏差，比如SCI或者BDI的平均值为300 mm,偏差值为30 mm(一般FWD的值略小于TSD的值)，界限范围最大值可为380 mm，而简单线性回归无法反应出这些偏差。随着人工智能的发展，基于神经网络法的优点，一些学者开始利用此方法进行TSD数据的分析，Elbagalati[23]等利用BP神经网络分析路易斯安那州及明尼苏达州的TSD与FWD实际测试数据，得到了将TSD测试数据转换为FWD数据的ANN模型，ANN模型进行验证时能达到拟合度为0.9的高精确度。Zihan[24]等为了利用TSD测量的弯沉值进行路面结构层模量反算分析，提出了一种基于力学原理的方法将TSD测量值转换成等效的FWD弯沉值，利用人工神经网络算法进行分析163组不同路面结构的TSD及FWD数据，回归分析得到ANN模型，并基于ANN模型开发了windows软件程序将TSD弯沉值转换为相应的FWD弯沉。而关于ANN模型的下一步工作应增加现场实际测试数据进行优化，可以得到不同路面条件对TSD检测结果的影响，这将有助于创建具有更强泛化能力的稳健网络。

在国内，《公路沥青路面设计规范》(JTG D20—017)中规定荷载作用中心弯沉值仍是新建路的验收指标，《公路沥青路面养护设计规范》(JTG5421—2018)中既有路面结构参数推荐可通过弯沉盆反演路面结构模量参与养护修复设计。而在《公路技术状况评定标准》(JTG 5210—2018)中路面结构强度是沥青路面技术状况评定内容之一，属于抽样检测指标，按路面养护管理需要确定抽样率，路面强度指数(PSSI)及路面结构强度系数(SSR)模型计算都是基于静载作用下的层状弹性体系及现场实测贝克曼梁(BB)测试值。故目前高速弯沉仪在国内的应用，主要是利用荷载中心的弯沉值与FWD及贝克曼梁(BB)进行换算。巩建[25]等利用试验路段将高速弯沉仪测值与贝克曼梁回弹弯沉进行对比分析，也发现二者存在良好的线性相关性。郑涛[26]将激光动态弯沉检测车应用于高海拔地区沥青混凝土路面，通过快速弯沉检测与实测数据分析，建立了与传统贝克曼梁法的线性方程换算关系。但是由于上述对比试验路段数据量小，分析方法较为简单，其相关结论适用性具有局限性。

上述分析中关于高速弯沉仪测试弯沉指标中对TSD与FWD荷载中心弯沉之间关系研究较多，而对于其他弯沉点之间的关系研究较少，应增加其他弯沉点D200,D300,D450,D900对比研究。且从长远来看，高速弯沉仪与FWD测试值之间的弯沉指标关系应建立在大量的实际工程数据基础上，采用不同的方法进行分析，充分考虑到各种因素对于二者关系的重复性以及可靠性的影响，如测试车行车速度、测试温度、路面类型以及路表特性，且根据需要做适当的调整，从而为二者建立统一的指标换算关系与评价方法。国内现有的路面结构强度评定指标计算模型仍利用的是贝克曼梁弯沉值，在规范未更新之前，高速弯沉仪与贝克曼梁之间的弯沉指标换算关系仍需重点关注。

3 高速弯沉仪的数据分析及应用

路面状况可归纳为功能性状况和结构性能状况，二者在路网的路面管理系统里面起着非常重要的作用，但是路面结构性能状况主要用于项目级评价，而在大多数的路面管理系统(PMS)中的公路网级评价中被忽略了。主要原因是传统的无损检测设备由于其效率低等原因使得收集网级水平的路面结构状况数据成为一个很大的难题。随着高速弯沉仪的出现解决了这一问题，路面结构性能状况指标未来将纳入到PMS系统中，作为路面养护以及维修等决策制定的判定依据。同时结合GPS定位系统，提高PMS系统的管理效率，可实现路面监测的动态管理。

3.1 路面弯沉指标与路表功能性状况的关系

Shrestha[16]等利用TSD测试数据计算的路面结构曲率指数SCI300与PMS数据库中的疲劳裂缝进行对比分析，TSD实测值计算的有效结构数与PMS数据库中基于结构层厚度、结构层系数等计算的结构数进行对比分析，结果表明路表TSD指数(SCI300)与路表状况(疲劳裂缝)相关性很小，从大体趋势而言，路面结构弱的部位一般有较多的疲劳裂缝，但是路面疲劳损伤不能作为评定路面结构承载能力的稳定性指标。作者在后续研究中利用弗吉尼亚州2017年8月以及9月的TSD测试数据(2 414 km的洲际公路以及4 055 km里的主干道)进行网级水平的路面功能性状况和路面结构性能状况的关系研究[27]，发现路面弯沉值指标对于路面车辙不敏感，而试验路段裂缝与弯沉值指标存在较复杂关系，利用澳大利亚道路研究所的智能检测车(iPAVe)搜集的路表状况及结构状况数据分析研究了网级路面状况与结构状况之间的关系[28]，同样得到的结论是在网级水平路面结构评定时，路面功能性状况不能很好地反映路面结构性能，二者参数指标之间无明显相关性。Zihan[29]等通过研究发现，仅用路表指数(裂缝、车辙、平整度等)或者这些指标的损伤率来识别路面结构破损部位是不可取的，因为这些路表状况指标与路面结构承载力存在相关性，但是相关性不强。Elseifi[18]等通过统计分析以及钻芯取样同时考虑结构指数及路面功能性指标，调研结果表明一些部位通过功能性指标评价是处于非常良好的状态，但是已经出现路面结构缺陷。从上述分析中可以看出路表功能性指标不能全面反映出路面的整体状况，应将结构性指数评估也纳入到路面管理系统中，仅以路表状况指数进行决策具有较高的风险，二者参与决策过程做出更好的养护决策，为国家节省大量经费，所以基于高速激光弯沉检测技术的路面结构指数研究具有重要意义。

3.2 基于激光高速弯沉测试的路面结构性能指标研究

在MEPDG设计法中为了预估路面结构性能，疲劳和车辙应变通常作为主要的路面响应指标。为了使TSD能够成功应用于PMS管理系统，通过TSD测试数据计算的指数须稳定且能够反映路面关键性响应。目前对于高速弯沉仪TSD测试数据主要用于评估公路网级的路面结构状况，Nasimifar[30]利用3D-Move 模型计算数据以及TSD现场测试数据对各种路面结构进行弯沉盆指标敏感性分析，研究发现TSD弯沉斜率指标DSI200-300(D200-D300)以及DSI300-900(D300-D900) 分别与疲劳应变(沥青层底最大拉应变)以及路基顶面最大压应变具有良好的相关性，以沥青混凝土层厚度进行路面结构分类，根据不同类别的路面结构建立这些弯沉斜率指标与路面结构关键性响应的关系式。美国联邦公路局2015年一项研究报告显示基于TSD测试设备的现场评估中，DSI指标相对于其他指标而言更准确[31]。

路面结构数SN能够表征预期荷载作用下柔性路面的结构承载能力，是美国路面设计工作中最常用的路面结构指标。有效结构数SNeff是服役路面的结构承载能力表征指标，一般通过无损检测技术(如AASHTO推荐的FWD测法)进行评估。在AASHTO设计指南中提出了基于FWD测试数据的SN与SNeff的计算公式，但是由于在网级路面结构评价中FWD与TSD的荷载布置的不同(单个平板VS双轮胎)，作用荷载的不同(冲击荷载VS滚动荷载)以及记录弯沉值不同(峰值VS时间同步值)，所以现有的评估SNeff的方法不宜直接使用，需要寻找适用于TSD测试数据的SNeff计算方法。Manoharan[32]等基于粒料基层柔性路面的结构性能状况研究建立了两个简单的数学模型，将TSD测试数据直接转换为FWD等效结构数，如式(25)～(26)。

(25)

(26)

式中，SNP为修正结构数(基于TSD测试数据的等效FWD结构数)；D0(TSD)为TSD测试最大弯沉值。

Zihan[33]等利用路易斯安那州和爱达荷州的两个测试项目的数据进行回归分析，得到了基于TSD测试数据的SNeff模型方程如式(27)：

SNTSD=18.67×e(-0.013×D0)+8.65×(D48)0.11+

0.18×(Tth)+0.31×Ln(ADT)-24.28,

(27)

式中，SNTSD为基于TSD测试的结构数；D0为轮胎作用下的弯沉或中心点弯沉；D48为离弯沉中心距离为1.22 m处的弯沉；Tth为路面结构的总厚度；ADT为日平均交通量。

Nasimifar[34]等提出了一种用于PMS网级水平评估的SN计算方法，该方法利用426种路面结构的黏弹性以及线弹性分析结果进行数据回归分析，得到基于TSD测试数据的现有路面有效路面结构数SNeff回归公式见式(28)～(29)：

SNeff=C1SIPC2HPC3，

(28)

SIP=D0-D1.5HP，

(29)

式中，D0为TSD测试荷载中心点弯沉；D1.5HP为TSD测试离荷载作用中心1.5Hp处的弯沉值；SIP为路面结构指数(μm)；HP为路面结构层总厚度(mm)；修正系数C1,C2,C3,C1=0.436 9；C2=-0.476 8;C3=0.818 2并提出了SNR指标，见式(30)。

(30)

SNR>1说明有足够的路面结构承载能力，SNR<1的路段部分需要进行加铺满足结构性需求。规定需求的结构数SNreq通过交通量以及路基模量计算，采用AASHTO1993设计指南推荐公式，见式(31)：

lg(ESALs)=zRs0+9.36lg(SNReq+1)-0.2+

(31)，

式中，ESALs为80 kN等效单轴数量；ZR为标准正态偏差(基于道路功能分类)；总体标准偏差(设计一般取0.45)；ΔPSI为设计寿命周期末允许服务质量降低量(柔性路面取值1.7)；Mr为路基回弹模量。

在高速激光弯沉测试数据分析与应用方面，国内相对比较滞后，对于传统弯沉测试数据利用率最高的是荷载作用点中心弯沉值，在用于公路网级评定时，需要将激光高速弯沉测试值换算为贝克曼梁测试值，而后利用路面结构强度指数(PSSI)进行路面结构性能评定，PSSI计算式见式(32)，路面结构强度系数见式(33)。

(32)

(33)

式中，SSR为路面结构强度系数，lR为路面弯沉标准值(0.01 mm)；l0为路面实测代表弯沉(0.01 mm);α0为模型参数，取值为15.71；α1为模型参数，取值为-5.19。但PSSI指标不参与路面技术状况指数(PQI)的计算，而巩建[25]等认为2007版《公路技术状况评定标准》没有体现路面弯沉在路面使用性能评价中的作用，认为规范需要完善路面使用性能综合评价指标，提出了将路面结构强度指数参与PQI计算的新模型，而现有《公路技术状况评定标准》(JTG5210—2018)依然未对此方面做出变动。而国内基于高速激光弯沉检测技术的路面结构性能指数的研究尚处于缺失状态，随着国内新版的《公路沥青路面设计规范》(JTGD50—2017)以及无损检测技术的更新发展，路面结构承载能力评定指标也应进行相应的更新与完善，而不应仅停留在传统测试设备与新型设备之间的线性换算。

3.3 基于激光高速弯沉测试数据的模量反算

高速弯沉仪(TSD)已被证明是网级路面结构评估中很有价值的检测技术，但是TSD数据在路面项目级的应用目前是非常有限的，路面性能反演的标准方法是基于FWD检测技术，虽然TSD与FWD检测技术类似，但是不能等同，所以TSD测试数据不能直接利用FWD反算软件来进行路面特性分析，所以近期一些学者开始了基于激光高速弯沉测试数据的模量反算研究。Nasimifar[35]等基于TSD数据利用两种方法对路面结构层的模量进行反算，其中一种方法为速度法，即利用TSD弯沉斜率结合三维动态分析软件(3D-Move)模拟进行路面结构层模量反算，这种方法的分析过程包括了黏弹性分析、非均布荷载布置以及移动荷载作用。但是由于3D-Move软件需要反复试算，需要的计算时间过长，这就限制了速度法在网级评价中的应用。而另外一种方法则是弯沉法，即根据弯沉算法计算弯沉值，这种算法是基于均布双圆荷载作用下的多层线弹性体系下的反算方法。而后Nasimifar[36]等采用分段三次艾米插值多项式(TUTC-PCHIP)的方法、韦伯函数方法(WFFM)、TSD算法计算路面弯沉,然后利用这3种方法进行结构层模量反算，虽然每种方法的弯沉值很接近，但反算的路面结构层模量有明显的差异。鉴于弯沉算法的局限性，弯沉法反算路面结构层模量的合理性取决于弯沉计算理论的有效性，而分析结果表明Greenwood的TSD算法相对于TUTC-PCHIP法、韦伯函数WFFM法而言，与斜率法计算的结构层模量值更接近。Elbagalati[23]及Zihan[24]等利用ANN模型，将TSD测量的弯沉值转换为等效的FWD弯沉值,然后换算后的弯沉值利用现有的FWD反算软件进行路面结构层模量的反算。经ANN模型转换后弯沉反算的路面结构模量与FWD测试弯沉反算模量具有较好的一致性，认为基于TSD测试数据的反算模量可以用于计算路面结构响应(应力应变分析)、路面疲劳寿命预测及结构健康监测。Nielsen[37]研发了TSD专用反算程序方法，此方法基于层状线性黏弹性路面模型，开发的反算程序如实模拟现场TSD测试，考虑了检测车的行驶速度、TSD实测时的阻尼和黏弹性效应，得到的模型结果值与实测值具有良好的一致性。

根据高速弯沉检测技术的评估和验证方面的有益成果，世界各地的交通机构都在考虑将弯沉测试路面结构的评估纳入到网级PMS中进行路面综合评估。而在路面结构参数分析基础上，最终如何高效且有效地实现TSD检测技术在网级路面管理系统中的应用也是一项重要工作，Rada[38]等联邦公路局资助的基金项目中对高速弯沉设备用于网级路面结构评定进行了研究，通过数值模拟分析以及美国明尼苏达试验路段的现场试验数据选择与应变相匹配的最佳弯沉指标，然后利用实测弯沉指标预估HMAC层底拉应变值，利用应变值来进行路面结构的充分性，并详细说明了TSD弯沉指标在PMS中的应用过程。Katicha[17]等在9个洲际公路管理机构验证了TSD的应用，利用9 656 km的现场实测数据分析TSD数据在PMS中的应用。Nasimifar[39]等在其现有的研究基础上，通过一个现场实际工程案例详细演示了研发的方法和软件程序(TDEPS)利用TSD数据在PMS中的应用，TDEPS处理分析TSD数据然后输出路面结构参数如经温度调整后的SCITSD-Ref及结构数SN，以用来调整或确认根据路表功能性指数决定的路面处治分类。弗吉尼亚州的交通运输部门目前立项了一个新的基金项目，研究目的是搜集高速弯沉(TSSD)检测数据并将其融入到国家PMS管理系统。

4 结论

随着高速激光弯沉检测技术的发展，国内外实际工程应用也将会越来越广泛。本研究总结了高速激光弯沉检测技术现状，这种技术仍未完全成熟，理论体系和评价方法的研究成果有待于向深度与广度的进一步推进和创新。特别就国内而言，理论体系、数据分析与应用方面的研究相对比较滞后，更需加强以下几个方面的研究工作。

(1)持续改进现有理论模型。基于大数据分析手段，搜集现场TSD检测数据，建立数据库，并考虑外部因素对测试结果的影响，对现有模型进行验证或修正。

(2)加强高速弯沉仪的数据分析及应用。目前开展的研究工作主要是高速激光弯沉检测技术在网级路面评价中的应用，后期应在现有的理论基础上加强其在路面项目级评价中的应用研究，并探索高速激光弯沉检测技术在刚性路面中的适用性，用于评估刚性路面结构承载力、荷载传递和接缝状况等。

(3)推动高速激光弯沉检测技术与路面管理系统的融合。高速激光弯沉检测技术融入到路面管理系统的方法尚未成熟，开展的研究工作较少，应加强研发TSD测试数据专用分析及处理方法与软件程序，确定PMS中如何利用路面结构指数与路面功能性指标实现路面性能综合评价的有效方法。

(4)推动高速激光弯沉检测技术与地理信息技术、影像分析技术的融合。目前，地理信息技术、遥感分析技术得到广泛应用，将以上技术应用于高速激光弯沉检测，开发相应的软件程序，可实现路面弯沉测试数据空间化、可视化，对路面病害精准定位，实现路面病害监测预警，将有助于合理的路面养护和修复管理等工作。

(5)完善适合国内路面结构的高速激光弯沉检测技术理论研究。国外主要的路面结构类型是全厚式沥青路面和粒料基层沥青路面，基层的刚度和强度较低。但我国的情况却恰好相反，大部分路面基层都是半刚性基层，其强度和刚度较高。柔性基层与半刚性基层在力学性质、结构层传荷能力、路表变形、结构层内应力应变等方面都具有较大差别，所以应针对我国典型路面结构进行相应的研究，提出适合国内路面结构体系的力学模型以及弯沉计算方法，在此基础上深化高速弯沉仪的数据分析及应用研究。

(6)进一步研究高速激光弯沉测试方法与其他弯沉测试方法的关系及其可靠性。国内高速激光弯沉测试与传统弯沉测试法之间的比较过于简单，应该选取我国典型的路面结构作为试验道路，基于已有的高速激光弯沉测试数据库，利用不同的分析方法，如采用数理统计学法、人工神经网络法等分析评估高速弯沉仪测量值与贝克曼梁(BB)、落锤式弯沉仪(FWD)测量值之间的关系并建立相应模型。且高速激光弯沉测试结果的利用率较低，现有的路面结构强度指数模型对于高速弯沉仪法是否适用有待进一步验证，应借鉴国外研究成果，开展高速弯沉仪在公路网级评价中的应用研究，分析其他弯沉指标用于路面使用性能的评价，对路面管理系统中路面技术状况评定方法进行完善，以便规范的更新。