深圳抽水蓄能电站机组转速与导叶开度变化规律研究及预防过速逻辑分析
胡文兴,李 青,俞家良,万 波,陈丹琪,裴 军
(深圳蓄能发电有限公司,广东 深圳 518115)
0 引 言
抽水蓄能电站调速器系统中,通常采用冗余配置来提高容错率。深圳抽水蓄能电站采用GE公司H-SHE- 00-MEU11-SA00FE- 01型调速器系统,该系统主要由UPC、SPC和TADT组成。UPC为调速器的核心处理单元,将输入到UPC的信号值经过计算后,可以给定相应的导叶开度并发送给位置随动控制器SPC;TADT与中央处理器UPC硬件结构完全一致,通过齿盘测速和残压测速采集的信号计算出机组实际转速,通过继电器输出开关信号至LCU,参与LCU流程控制,同时输出4~20 mA的模拟量转速信号至LCU。
图1是位置随动控制器SPC双环反馈控制流程。该过程中实时采集比较导叶开度设定值、机组导叶实际开度值(Servomotor position)和主配压阀实际位置(Valve position)。经过一系列PID计算和有效性限制后,输出主配压阀开启命令。因此准确采集机组导叶实际开度和主配压阀实际位置直接关系到SPC能否输出合理的主配压阀开关命令。当导叶开度反馈传感器发生故障时,不能真实准确的反应导叶实际开度,将会导致机组误调误控,甚至引起机组过速等严重后果;在极端情况下,还可能诱发机组飞逸等安全事故。因此研究和判断导叶开度反馈传感器开度信号的真实性,对实际应用有着极其重要的价值。
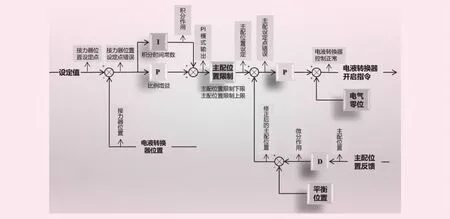
图1 位置随动控制器SPC双环反馈控制流程
1 异常升速识别方法
在工程实际中,通常需要分析多种数据之间的内在联系,通过数学分析寻找变量之间的函数关系。如果面对较多的观测数据点,需要根据观测数据样本空间的大小选取拟合次数的大小,若拟合次数选取的过小或过大,则会出现拟合效果不佳或过拟合的情形[1]。曲线拟合方法在求解确定性关系函数时有良好的效果,如果求解微分方程,还可以解决非确定性关系函数。在工程实际中,变量之间没有准确的相关关系,在处理这些问题时,我们可以利用样本数据,假定变量函数,通过整体逼近的方法求解拟合曲线,从而反映变量间的相关关系和变化趋势。因此,在工程实际中曲线拟合方法具有特别的价值。
为进行分析,本文采集了深蓄电站4号机组125组发电开机数据,其中包括2组因导叶开度反馈传感器损坏造成的机组异常升速数据和123组正常开机数据(包括2组机组在低水头下开机数据和2组高水头下开机数据)。通过数值分析机组转速随导叶开度、时间和水头的变化规律,最终用曲线拟合的方法找到了以时间为自变量的转速拟合曲线,并进一步用概率统计的思想设置合理置信区间,得到上下阈值。机组转速超过阈值时,则判定为导叶开度反馈出现故障。该方案可以及时发现因导叶开度反馈传感器损坏造成的机组异常升速过程,减小机组异常升速时间,避免机组过速,保障机组安全运行。
2 转速曲线趋势的分析
为便于理解内在逻辑关系,先简单地定性分析导叶开度、水头和时间对机组转速的影响。首先,从水头角度考虑,我们对比了4组不同水头下的机组转速数据,分别为125组数据中的两组最高水头和两组最低水头,结果如图2所示。
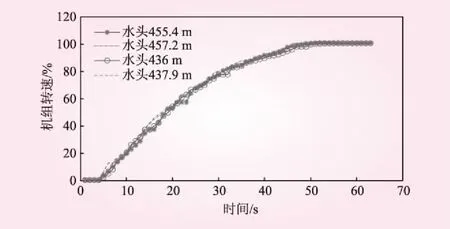
图2 不同水头对转速的影响
从对比结果可以看出,高水头比低水头更快达到额定转速,到达时间分别约为48 s和50 s。但两组曲线差距较小,甚至低于随机扰动造成的突变量,因此在我们生产实际中所达到的高低水头下,机组转速变化趋势基本保持一致。
接着我们对导叶开度进行分析,为了便于观察,我们将123组正常开机状态下的机组转速数据求平均值,如图3所示。
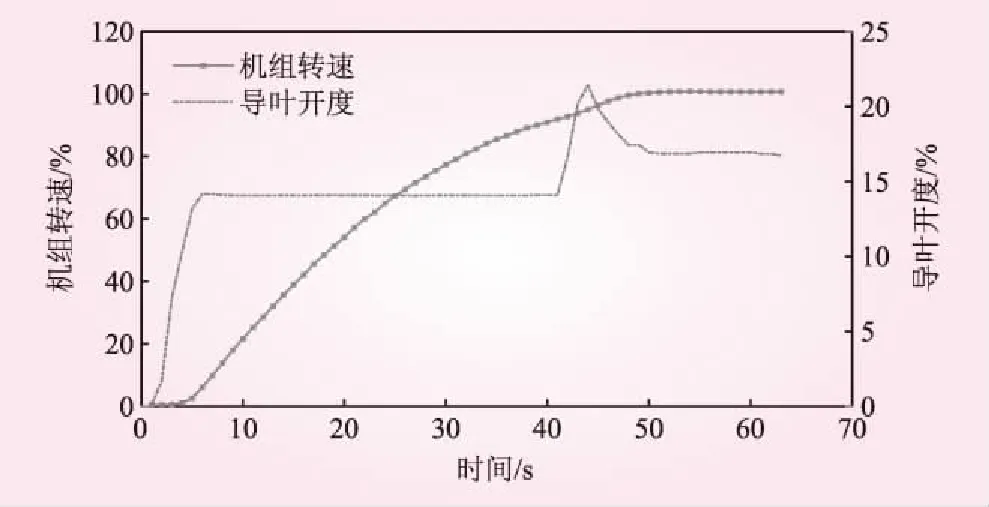
图3 机组转速平均值与导叶开度度的关系
按照机组设定,导叶开度变化过程分为四个阶段,第一阶段导叶开度度快速打开到14%,对应于0到7 s之间,机组转速上升,加速度逐渐增大。随后进入约30 s的保持阶段,机组转速持续加快,但加速度逐渐回落。当40 s左右,导叶开度再次短时间内增到21%左右,转速增加的同时,我们观察到加速度再次攀升。最后,导叶开度回落并保持在17%,机组转速也不再增加保持在100%左右。因此,导叶开度度决定了转速的最终稳定值。
图4为125组机组转速随时间的变化曲线,其中包括2组故障数据。从图中可以看到,转速与时间存在连续的函数关系,且不同的水头下趋势一致。系统导叶开度设置固定,实际应用的水头范围对转速曲线走势影响较小,因此拟合转速随时间的函数,可以有效反应当前系统转速变化趋势。

图4 机组转速与时间关系
3 机组转速线性回归
这里我们采用梯度下降法,对123组正常开机状态的转速样本曲线进行线性回归。通过观察,该转速与时间的曲线满足多项式。首先,我们假设机组转速与时间的关系式为
(1)
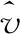
(2)
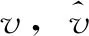
(3)

ak+1=ak-λ∘∇g
(4)
λ=[λ0,λ1,λ2,λ3,λ4,λ5]T为回归系数,运算符“∘”为哈达玛积,使两个向量对位相乘。找到合适的λ,会使每一次迭代都向梯度下降的方向靠拢,即L减小的方向。应用该梯度下降法,得到的一组合适的系数,其中a0=-0.310 834 850 875 394,a1=1.031 487 922 807 307,a2=0.151 488 250 066 986,a3=-0.003 440 281 082 441,a4=-0.000 011 590 589 849,a5=0.000 000 560 449 180。曲线拟合结果如图5所示。

图5 机组转速线性拟合结果与上下阈值
4 阈值设定
通过图5可以看出,机组转速值在拟合曲线周围小范围区域内随机扰动,这时利用统计学中的概率思想,来刻画实际值与预估值之间的偏移量。为了找到合理的阈值,我们首先分析样本数据每一个时刻的方差,结果如图6。观察可以发现,方差的整体趋势与时间负相关,在导叶开度突变的时间点,会瞬间增大。因为方差反映了系统的不确定度,方差越大机组转速不确定度越大。因此,合理的方差取值应全部大于样本方差。图6给出了样本数据实际的标准差,为便于阈值计算,我们选取了一条在所有标准差上方的关于时间t的一次函数作为标准差σt,公式为
σt=γ1t+γ2
(5)
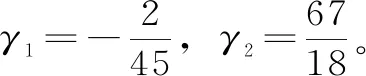
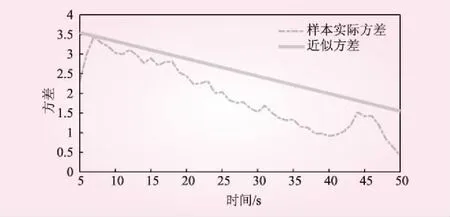
图6 实际样本方差曲线与近似方差曲线
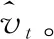
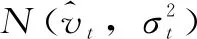
转速上限
(6)
转速下限
(7)
公式中各系数前面已经给出。我们以置信水平为0.999 9为例,查表得系数α=3.890 591 886 413,通过公式6求得上下阈值曲线,结果如图5所示。上下阈值可以完全覆盖123组机组正常状态下的转速曲线,没有误判。同时,我们也可以观察到两组故障曲线,超出了上限阈值,可以被区分判别出。且第一次超出边界时转速小于60%额定转速。因此实时对比当前转速和式(6)、(7)给出的转速上下阈值曲线,在99.99%的情况下能够快速识别机组异常升速现象。在实际应用中,可以在监控系统设置一组防过速逻辑:在机组升速阶段,当机组转速超出公式(6)、(7)给出的转速上下阈值曲线范围时,监控系统输出异常升速报警;该报警保持2S未复归时可触发事故停机,及时识别并阻止机组异常升速,避免过速。
5 结 语
根据深圳抽水蓄能电站机组运行实测数据,分析转速随导叶开度、时间和水头的变化规律,我们可以通过线性回归方法,拟合出转速随时间的变化规律,并给出指定置信区间下的上下阈值曲线。在实际生产中,通过检测转速是否落在置信区间内,可以简单有效的判别转速是否异常。因此,这种数学模型和分析方法,可以为抽水蓄能机组预防机组异常升速提供科学依据。且该方法具有普适性,当给定一个蓄能机组后,我们可以通过此方案找到对应的回归曲线和阈值。

