如何正确运用χ2检验——三种R×C列联表资料的CMH χ2检验

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

在横断面设计的二维列联表资料或称为R×C列联表资料中，根据两变量是否为有序变量，可以归纳出三种不同的二维列联表资料：①双向无序R×C列联表资料；②结果变量为有序变量R×C列联表资料；③双向有序且属性不同R×C列联表资料。对其进行统计分析的方法分别为“独立性假设检验”“秩和检验”和“相关分析”，它们可以被概括成一种统计分析方法，即CMH χ2检验。本文介绍广义CMH χ2检验统计量及其三种变形，并基于SAS软件实现统计计算。

1 适合进行CMH χ2检验的三种R×C列联表资料的实例

1.1 双向无序R×C列联表资料的实例

【例1】文献［1］中有一个双向无序R×C表资料（说明：不考虑“时间”的有序性），见表1，试分析“条目”与“时间”之间是否存在关联性。

表1 基层精防医护人员K6评定结果

1.2 结果变量为有序变量R×C列联表资料的实例

【例2】文献［2］给出了如下临床资料：比较三种对肥厚性鼻炎（HR）治疗方法的效果。将162例HR患者分为三组，A组（n=56）行下鼻甲骨黏骨膜下切除术，B组（n=43）行下鼻甲部分切除术，C组（n=63）行下鼻甲黏膜下微波热凝术。治疗效果见表2。试对三组治疗效果进行比较。

表2 三组下鼻甲手术治疗的临床效果

1.3 双向有序R×C列联表资料的实例

【例3】在文献［3］中，为探讨新冠肺炎疫情期间居民急性应激障碍（ASD）症状的检出情况及影响因素，得到有效问卷16 048份，有效问卷回收率为72.83%。在该研究中，因素“媒体暴露情况（时间）”与结果变量（出现ASD症状的程度）之间的数量关系如表3所示。试分析“媒体暴露情况（时间）”与“ASD症状的程度”之间是否存在线性相关关系。

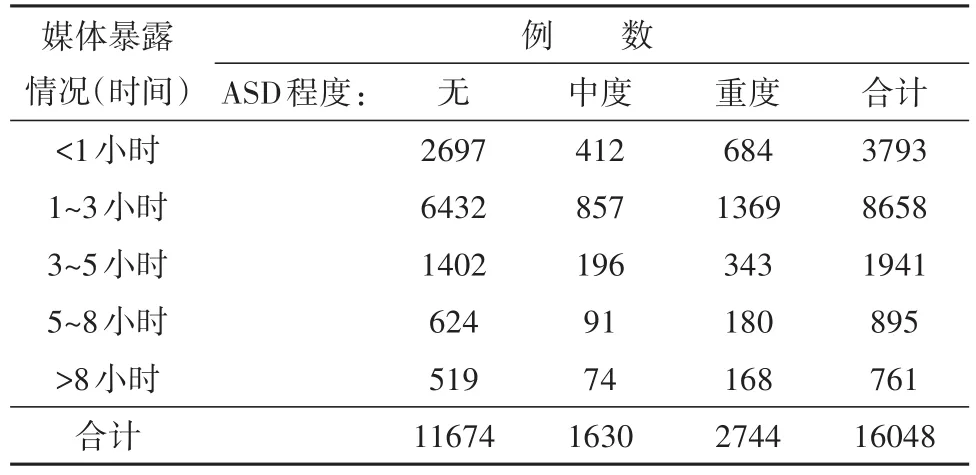
表3 媒体暴露情况（时间）与ASD症状检出情况的调查结果

2 CMH χ2检验的检验统计量及其三种变形

2.1 “CMH”的含义

“CMH”是“Cochran-Mantel-Haenszel”的缩写，即采用三位作者姓名的第一个字母来命名该分析方法 ，实际上，Cochran、Mantel、Haenszel、Mantel、Birch、Landis、Heyman和Koch都对该分析方法做出过贡献［4］。

2.2 广义CMH χ2检验统计量的定义

一般来说，CMHχ2检验统计量是为分析高维列联表资料而构造出来的。将高维列联表资料按某一个或多个因素进行分层，每层都应该是规模相同的R×C列联表资料。下面以表4形式表示第h层的R×C表，h=1、2、…、q。q为层数，R为行数，C为列数。

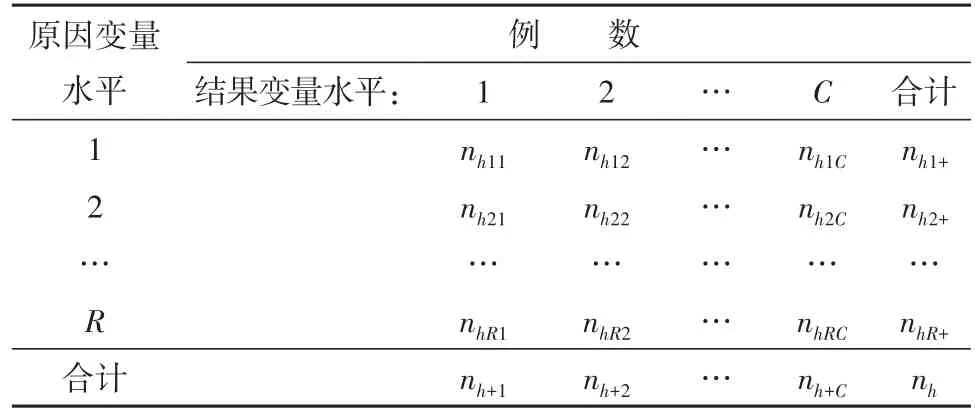
表4 第h层R×C列联表的列表格式

广义CMHχ2检验统计量［4］定义如下：

需注意的是，当各层间效应方向不一致时，CMHχ2检验统计量的检验功效很低。

2.3 广义CMH χ2检验统计量的三种变形

2.3.1 概述

式（1）是以矩阵形式呈现的计算公式，很不直观。由于它试图达到高维列联表资料的多种不同分析目的（例如独立性分析、相关性分析、差异性分析），故其隐含诸多前提条件，包括“是否存在有序变量”“如何给有序变量赋值”。基于不同的前提条件，就会产生出不同的统计计算公式。为了直观起见，现假定只有一层，即一个二维R×C列联表资料，基于不同的前提条件，将式（1）转变成三种具体的、直观的检验统计量。

2.3.2 与备择假设为“非零相关”对应的检验统计量

若拟分析的资料如本文表3（即双向有序R×C列联表资料）所示，此时式（1）就简化成下式：

2.3.3 与备择假设为“行平均评分不同”对应的检验统计量

若拟分析的资料如本文表2（即结果变量为有序变量R×C列联表资料）所示，此时式（1）就简化成下面两个式子之一：

在式（3）中，“∝”代表“呈正比”；当给R×C列联表的列变量（即结果变量）赋值或评分时，若按“表评分”方式评分，就采用式（3）（即单因素R水平设计一元定量资料方差分析）计算［4，7］；否则［包括“rank（秩）评分”“Ridit评分”和“修正的Ridit评分”］，就采用式（4）（即单因素R水平设计一元定量资料Kruskal-Wallis’s H秩和检验）计算［4，7］。在式（4）中，ni与Mi分别代表第i组中的“样本含量”与“秩和”。

在式（3）中，可对F统计量进行变换，见下式：

通过对式（5）变形，可以得到下式［8-9］：

式（6）的含义是：采用单因素R水平设计一元定量资料方差分析得到的检验统计量F值后，乘以组间自由度df组间所得到的结果，近似服从自由度为df组间的χ2分布。

2.3.4 与备择假设为“一般关联性”对应的检验统计量

若拟分析的资料如本文表1（即双向无序R×C列联表资料）所示，此时式（1）就简化成下式：

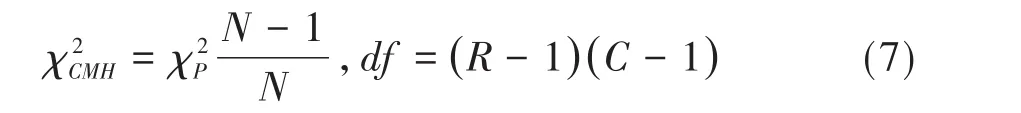
3 CMH χ2检验的SAS实现

【例4】沿用例3的资料，试将其分别视为“双向有序R×C列联表资料”“结果变量为有序变量R×C列联表资料”和“双向无序R×C列联表资料”，同时对其进行CMHχ2检验。基于“表评分”算法所需要的SAS程序如下：

以上是基于“表评分”算法所得CMH χ2检验的三种计算结果，分别对应三种不同的备择假设：第一种，“非零相关（即行、列两有序变量之间具有非零的相关关系）”，=6.635，df=1，P=0.0100；第二种，“行评分均值不同（即各行上有序结果变量的评分值的平均数不等）”，=33.7083，d f=4，P＜0.0001；第三种，“常规关联（即行、列两无序变量之间存在关联性）”，=36.6435，df=8，P＜0.0001。

以上三种检验都得出P＜0.01，故接受备择假设。对本例而言，可以认为：①“媒体暴露情况（时间）”与“ASD程度”之间存在“非零相关”，具体地说，随着媒体暴露时间延长，出现重度ASD症状的比例呈非线性上升趋势；②五种不同媒体暴露时间所对应的平均ASD值是不相等的，除第2个时间段之外，其他4个时间段都随着“暴露时间延长”，平均ASD值变大（即ASD症状程度逐渐加重）；③媒体暴露情况（时间）与ASD程度之间存在关联性（前面的“①”和“②”可以清楚体现出两变量之间是如何关联的）。

4 给有序变量评分的方法

4.1 表评分方法

在前面的SAS程序中，在“tables语句”中出现了选项“SCORES=table”，其含义是用表格里规定的方式给有序变量评分。这里的“表格”，其实是指SAS程序中如何给“行变量”或“列变量”赋值。“DO A=1 TO 5；”就是让“行变量 A”依次取 1、2、3、4、5分；同理，“DO B=1 TO 3；”就是让“列变量B”依次取1、2、3分。当然，也可以给变量A或B赋任意的几个由小到大的数值，例如“DO A=0.1，1.2，13.5，21.8，34.6；”。

4.2 其他评分方法

在SAS/STAT的FREQ过程中，还有另外三种评分方法，分别为“rank评分法”“ridit评分法”和“修正的ridit评分法”，对应的选项依次为“SCORES=rank”“SCORES=ridit”和“SCORES=modridit”。

4.3 评分方法与检验统计量计算方法之间的关系

对“常规关联”的计算结果而言，四种评分方法所得计算结果是完全相同的，因为计算公式中不涉及“评分”；对“非零相关”的计算结果而言，“表评分法”（采用Pearson’s相关分析）与另外三种评分法（其结果是一样的，采用Spearman’s秩相关分析）计算结果可能相差很大、甚至结论相反；对“行评分均值不同”的计算结果而言，“表评分法”（采用单因素R水平设计一元定量资料方差分析）与另外三种评分法（其结果是一样的，采用单因素R水平设计一元定量资料Kruskal-Wallis’s H秩和检验）计算结果稍有差别。例如，例4“基于秩评分”的结果如下：

【说明】“ridit评分法”和“修正的ridit评分法”输出结果与“基于秩评分”方法输出结果相同，此处从略。

注意：“非零相关”的结果与前面“基于表评分”的结果相反；四种评分法对应的“常规关联”结果都是χ2=36.6435、P＜0.0001；四种评分法对应的“行评分均值不同”有两个不同的计算结果，分别为“χ2=33.7083［采用方差分析计算再基于式（6）转换的结果］”与“χ2=31.2716（采用 Kruskal-Wallis’s H秩和检验计算的结果）”，但P值都小于0.0001。

5 讨论与小结

5.1 讨论

在给“scores=”选项指定“table”或其他三种非参数评分法（即rank、ridit和modridit）时，为什么“非零相关”有两个完全相反的结果？原因在于：前者采用的是“Pearson’s相关分析”，而后者采用的是“Spearman’s秩相关分析”。就例3资料而言，分别基于“Pearson’s相关分析”与“Spearman’s秩相关分析”得到“r=0.02033”与“rs=0.00568”。依据式（2）可算出对应的CMH χ2值分别为6.632368（与前面相应的计算结果6.6350很接近）和0.517715（与前面相应的计算结果0.5174很接近）。

在“常规关联”的分析中，将有序变量视为无序变量或名义变量，故给“scores=”选项指定四种内容（即table、rank、ridit和modridit）时，所得结果完全相同。就例3资料而言，。它在本质上就是=36.6458（即Pearson’s拟合优度χ2值），由式（7）可知：

在备择假设为“行评分均值不同”时，SAS/STAT中FREQ过程将此时的资料视为“单因素R水平设计一元定量资料”。若采用“表评分（即scores=table）”，则SAS/STAT中FREQ过程采用“单因素方差分析”；若采用其他三种评分，SAS/STAT中FREQ过程采用Kruskal-Wallis’s秩和检验。事实上，就是把结果变量B视为“定量变量”，因此，对结果变量B的赋值方法不同，将直接影响R×C列联表资料各行上结果变量平均值的计算结果。四种评分方法对应结果变量B的3个评分值如下：

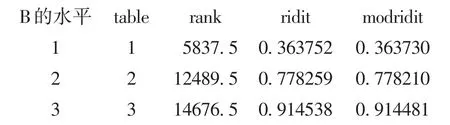
若直接采用SAS/STAT中ANOVA过程计算，得到F=8.44、df=4，基于式（6）可算得≈ 8.44 × 4=33.76，与“scores=table”对应的“行评分均值不同”时的“=33.7083”比较接近；若直接采用SAS/STAT中NPAR1WAY过程计算，得到H=31.2716，与“scores=rank”对应的“行评分均值不同”时的“=31.2716”完全相同。

值得一提的是，在分析二维列联表资料时，三种非参数评分法输出的三种检验结果相同；但若是分析高维列联表资料，情况就不尽相同了。因篇幅所限，此处从略。

5.2 小结

本文呈现了三种R×C列联表资料的实例及其三种相应的统计分析方法，这些方法可概括成广义CMH χ2检验；基于SAS/STAT中FREQ过程对R×C列联表资料进行分析时，可同时输出三种统计分析结果；本文还详细揭示了选取不同的“评分”方法，将会影响“非零相关”与“行评分均值不同”计算结果的真实原因。