基于频率法对钢箱提篮拱桥吊杆索力测试研究

易登军， 刘新文

(1.中交第二公路勘察设计研究院有限公司， 湖北 武汉 430056； 2.苏交科集团股份有限公司)

钢箱提篮拱桥主要由拱肋、吊杆、桥面系和横撑4部分组成，拱肋是主要的承力构件。吊杆作为提篮拱桥拱肋与桥面系之间的主要传力构件，在提篮拱桥结构中起着关键性的作用。与斜拉桥的斜拉索、悬索桥的主缆及吊索、施工中的缆索一样，系杆拱桥的吊杆索力是极其重要的参数，对吊杆索力测定的精确与否直接关系到施工控制的顺利实施和桥梁在运营期间的准确监测，因此索力测试也越来越被重视。

在实际工程中，精确测定钢箱提篮拱桥索力是一个比较复杂的过程。国内外学者在索力测试频率法的研究方面也做了大量研究。方志等在研究频率法识别索力时，分别讨论了拉索的刚度、垂跨比、不同边界条件以及在拉索上安装减振器等因素对频率法索力识别结果的误差分析，最后得出只要合理确定拉索的计算长度，就能利用振弦理论公式识别出精度较高的索力，但缺点是没有给出拉索合理计算长度的计算公式；宋一凡等引入动力计算长度概念，将两端固结的拉索振动模型动力等效为两端铰接的拉索振动模型；许俊采用环境随机振动法进行斜拉桥振动频率测试，然后采用有限元程序计算并通过简化计算公式修正，得出计算拉索索力。但对于短索而言由于刚度较大，采用近似计算误差大，而且随着频率阶数的提高，误差显著增大，要使误差尽可能小，宜采用低阶频率；段波等提出采用循环迭代来消除刚度的影响，但是没有进一步结合工程实例与实测结果分析比较来论证其可行性；苏成等通过有限元及样条拟合技术获取斜拉索索力与频率的对应关系，以工程实例为研究背景提出了一种基于多阶频率测试结果的斜拉索抗弯刚度识别方法；毛亚娜等研究了单侧安装阻尼器对吊杆振动模态的影响，提出了消除阻尼器对索力测试精度影响的计算方法，分析结果表明，该方法能广泛应用于频率法测估各种系杆拱桥的吊杆索力。

以上学者基本采用均匀拉索的振动模型，忽略了拉索锚头部分的刚度及其单位长度的质量与柔性索段的差异，且大多数研究在计算公式中考虑了抗弯刚度的影响，但由于实际吊杆的内部构造、钢丝黏结程度和索力大小等因素都会影响吊索刚度的计算，因此吊杆的抗弯刚度计算十分困难，容易造成误差；此外，相对于斜拉索，提篮拱桥吊杆相对较短，其线刚度集度(EI/l2)相对较大，这对频率法有不容忽视的影响。

该文充分讨论频率法相关理论、合理选择吊杆计算长度，最终推导出考虑抗弯刚度但不含抗弯刚度的索力计算公式，并通过实桥吊杆索力测试，与油压千斤顶法及索力动测仪法对比分析，以确定方法的可行性。

1 吊杆索力测试原理

1.1 索力动测仪的测试原理

实际工程中采用索力仪测试吊杆张拉过程中的索力，索力动测仪采用频率法进行索力测试，其工作原理为：

(1)

式中：f为弦的自振频率；l为弦长(m)；m为弦的材料线密度(kg/m)；T为弦的拉力(N)。

根据式(1)的张弦振动公式可知，弦的材料和长度获知后，在测得弦的自振频率后，可以计算弦的拉力。

对于两端固定质量均匀的钢索可以近似看作弦，钢索拉力T与基频f的关系为：

T=kf2

(2)

式中：k为比例系数，可按k=4ml2/1 000计算(l为钢索两锚固点之间的长度)；f=fn/n，fn为主振频率，n为主振频率的阶数。

索力系数k的计算公式是在作了如下假设后推导出来的：① 钢索只能受弯；② 钢索振动时没有其他外力作用，且横向位移非常小；③ 钢索全长质量均匀；④ 钢索两端嵌固。k=4ml2/1 000的计算值仅为理论近似值，如果现场条件允许可利用油表读数进行标定得到较精确的结果。

由式(2)可知：由油表读数得出T，索力动测仪测出f，而由式(1)可知f仅与计算长度l和索力T有关，对于同组吊杆，计算长度是相同的，则同组吊杆的f仅与T有关，又根据公式k=T/f2，同组吊杆的索力系数k值是一常数，不随张拉过程中索力的改变而改变。根据实测数据可反推吊杆索力系数k和吊杆对应基频。在实际吊杆张拉过程中可利用理论计算得来的索力系数k作为索力仪中的索力系数，根据理论基频大致判定吊杆张拉力是否接近目标值。

1.2 频率法的基本原理

吊杆简化假定如下：

(1) 吊杆在面内振动和面外摆振不具有耦合性，可以看成平面问题。

(2) 振动引起的挠度远小于吊杆的静载挠度。

基于上述假定，可建立如图1所示吊杆振动模型。

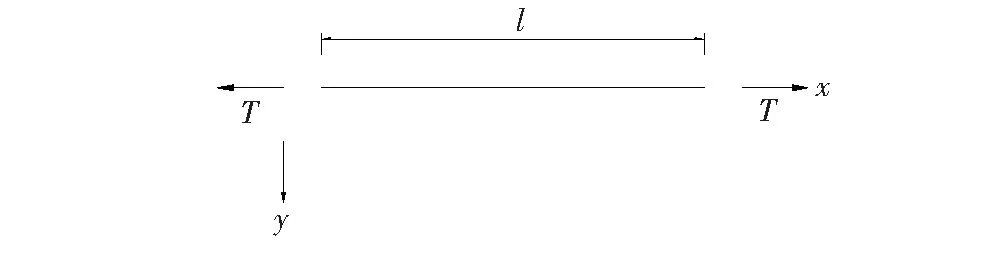
图1 吊杆振动模型

应用结构动力学原理建立吊杆振动微分方程：

(3)

式中：EI为吊杆的抗弯刚度；y(x,t)为吊杆的振幅；T为吊杆张拉力；m为吊杆的线密度。

为了方便起见，工程上往往把吊杆看作两端铰接，由文献[4]可知两端铰支边界条件下索力与自振频率之间的关系式：

(4)

式中:fn为吊杆的第n阶频率；n为频率的阶数；l为吊杆的计算长度。

式(4)就是两端均为铰接的吊杆张力计算公式，从公式可知在实际工程中，若能准确得到吊杆自振频率和抗弯刚度就可以准确计算出吊杆张力值。公式的第二项即为吊杆抗弯刚度对吊杆张拉力的影响量，该影响量随着频率阶数的减小和吊杆长度的增大而减小。当吊杆长度足够长时或采用低阶频率计算时，吊杆抗弯刚度的影响可以忽略不计，此时式(4)变成：

(5)

式(5)即为经典的振动理论计算索力的公式。在实际工程中往往吊杆长短不一，而且长度差异较大，其中也有很多短吊杆。对于钢箱提篮拱桥而言，靠近拱脚附近的吊杆往往长度较短且刚度较大，此时若忽略抗弯刚度的影响计算值会比实际值偏大。同样地对于两端铰支的吊杆，吊杆的振动频率受弯曲刚度的影响，相邻两阶频率的差值不会刚好等于基频，而且对于同一根吊杆其振动阶数越大弯曲刚度对振动频率的影响也会越大。

2 两端铰接吊杆索力计算

考虑到某些吊杆在索力计算时抗弯刚度的影响不能忽略，在实际工程中吊杆抗弯又不易识别，因此有必要在考虑抗弯刚度的情况下推导出无需使用抗弯刚度的索力计算公式。

令t、n均为正整数，且n>t。当式(4)中的n=t时，式(4)变为：

(6)

利用式(4)和(6)消去EI可得用两阶固有频率表示吊杆拉力T的公式：

(7)

式中：fn、ft分别为吊杆的n阶、t阶振动频率。

特别地当n=2、t=1时可得到利用吊杆频率1阶和2阶振动频率计算吊杆索力计算公式：

(8)

3 实桥索力测试分析

3.1 工程概况

蔡家坡跨渭河特大桥为主跨180 m的中承式钢箱提篮拱桥，其主桥孔跨布置为(50+180+50) m。主桥拱肋采用主、副拱肋双悬链线的形式，拱肋截面为宽度相等的钢箱截面，主、副拱肋截面在距离跨中74.2 m处(分叉点)合二为一，从分叉点到拱顶为等宽变高截面。拱肋每侧各布置24个吊耳，同侧吊点间距为6 m，每个吊点上设置有对应的上下耳板，每对耳板顺桥向布置2根吊杆，上游侧吊耳从南岸→北岸编号为DR1、DR2、…、DR24,下游侧吊耳从南岸→北岸编号为DR1′、DR2′、…、DR24′,上游侧吊杆从南岸→北岸编号为D1、D2、…、D48, 下游侧吊杆从南岸→北岸编号为D1′、D2′、…、D48′，全桥共布置96根吊杆，由于吊杆对称布置，因此吊杆D1、D2、…、D48与吊杆D1′、D2′、…、D48′参数一样，以下不再赘述。吊索和拱肋、纵梁采用插耳式锚固连接。渭河大桥主桥布置图如图2所示，吊杆的布置及编号如图3所示，吊杆构造图如图4所示。

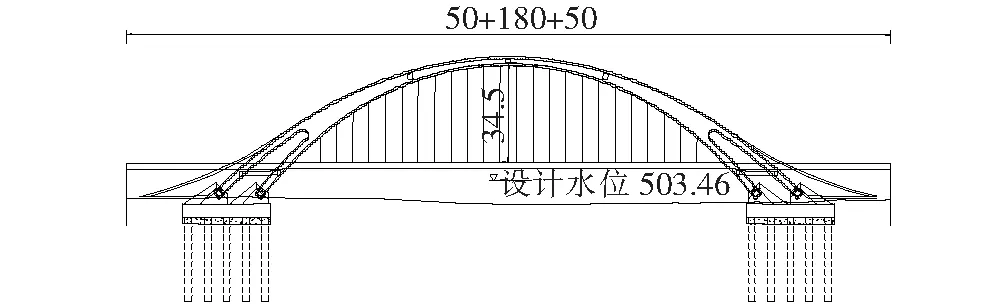
图2 大桥立面图(单位：m)

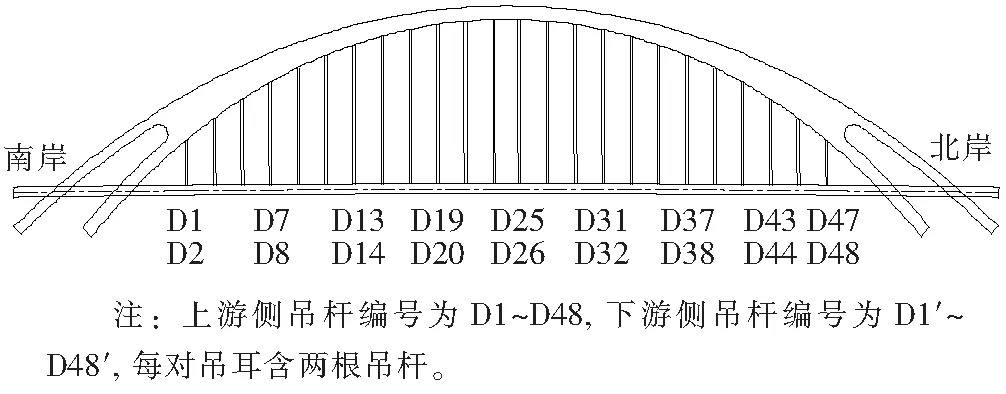
图3 吊杆纵向布置图

3.2 吊杆计算长度的选择

吊杆计算长度取值及构造如图4所示。根据索力动测仪中理论索力系数的计算公式，吊杆长度取参与振动的吊杆长度。对于吊杆两端由插耳或冷铸端头连接的吊杆，吊杆两端连接件体积较大或自重较大时，可取去除连接件后的吊杆长度作为吊杆计算长度。若知油压千斤顶油压表读数,则可由该设备的回归方程求得索力，再用索力动测仪测得该吊杆基频，则由式(2)可以反推出索力系数实测值k，而索力系数理论值由公式k=4ml2/1 000算得。吊耳DR1、DR24上的吊杆全长为8.617 m，吊耳DR2、DR23上的吊杆全长为13.302 m,这些吊杆均具有吊杆直径大、长度短、两头连接构件自重大的特点。图5为计算长度取值对索力系数k的影响图。

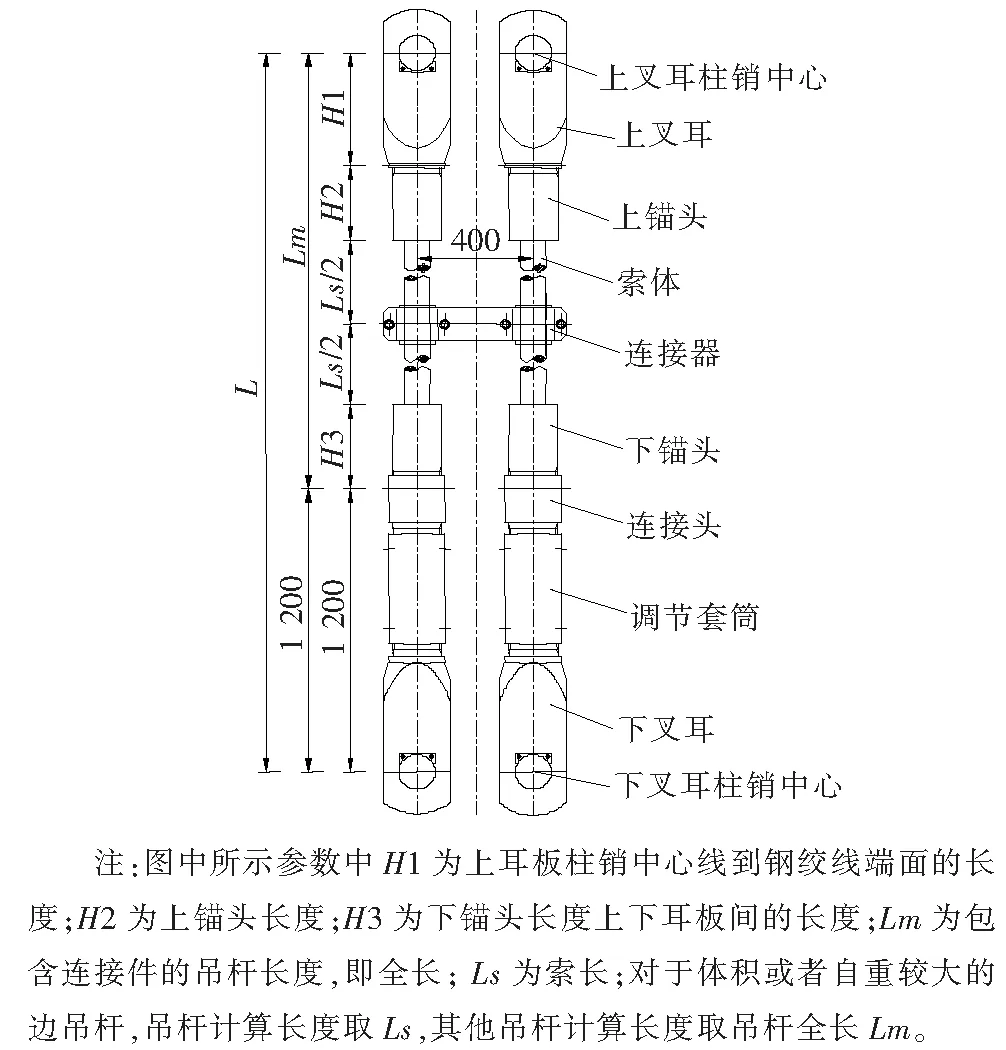
图4 吊杆构造图(单位：mm)

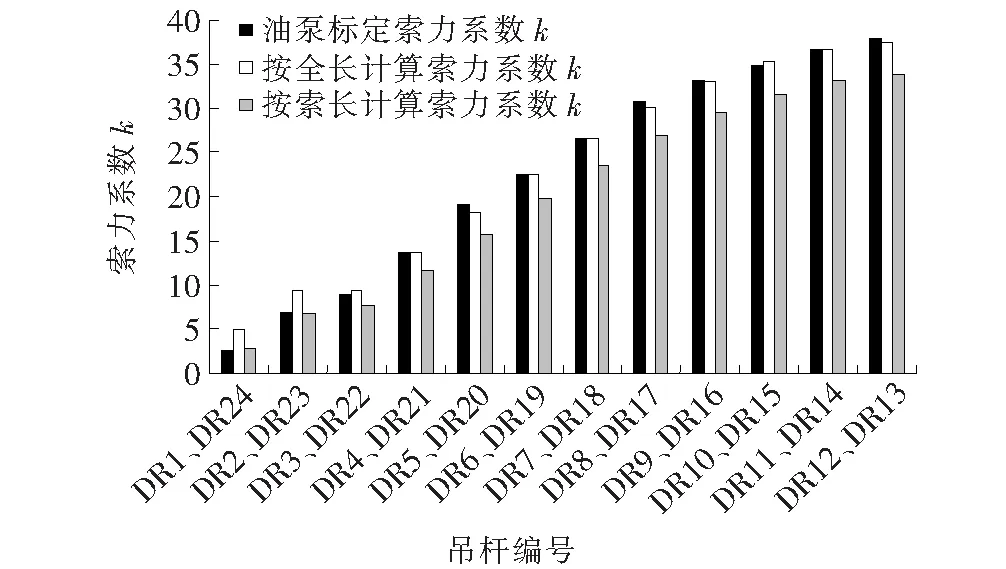
图5 计算长度取值对索力系数k的影响

由图5可知：计算长度取为吊杆的索长时计算所得索力系数k与实际油泵标定法相差较小。由此可见，两端连接件体积或者自重较大的吊杆，即全长小于13.302 m的吊杆，可取吊杆索长作为吊杆计算长度，其他吊杆取包含连接件的全长为计算长度。

3.3 索力动测仪、频率法、油压千斤顶法对比分析

该桥吊杆的初张在拱肋定位支架拆除完成之后，桥面系支架拆除之前进行。在吊杆张拉之前先安装吊杆，待全桥吊杆安装完成后开始进行吊杆的张拉。在张拉之前需要对液压千斤顶的油表进行标定，每套张拉设备对应一个回归方程，利用该回归方程可将千斤顶的张拉力转换成油表示数，在实际过程中可根据油表读数和设计值大致判定吊杆是否张拉到位，由油表读数换算成的索力值近似于设计值。

在实际索力测试过程中，油压千斤顶法所测得的张拉力可由油压千斤顶油表读数和该油压千斤顶对应的回归方程得到；利用索力动测仪可以得知吊杆基频，而由3.2节可以由油压标定得到较为精确的索力系数k值，而索力动测仪可以较精确地测得基频，故索力动测仪测得索力的误差主要由索力系数k引起，利用式(2)可以求得较为精确的吊杆索力；同样利用索力动测仪可以测得1阶自振频率和2阶自振频率，由式(8)得出索力。

由于篇幅有限，图6和表1为部分吊杆在张拉过程中的索力动测仪测量结果与油表读数换算索力对比数据，由表1不难看出：索力动测仪测得的结果与油表读数换算结果误差较小，最大误差为1.45%，小于5%的张拉精度要求。

图6 索力动侧仪与油压千斤顶测得索力值对比

表1 索力动测仪误差

图7、表2为部分吊杆在安装完成时的索力动测仪测量结果与频率法公式计算结果对比数据，由表2可知：索力仪测量结果与频率法公式计算结果相差不算太大，最大误差为4.24%，小于5%。分析两者的误差来源主要为：① 吊杆的频率测量存在误差；② 吊杆的索力系数计算存在误差；③ 利用频率法计算吊杆索力时吊杆的计算长度取值不当。

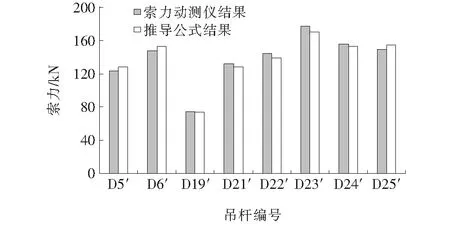
图7 索力动侧仪与推导公式结果对比

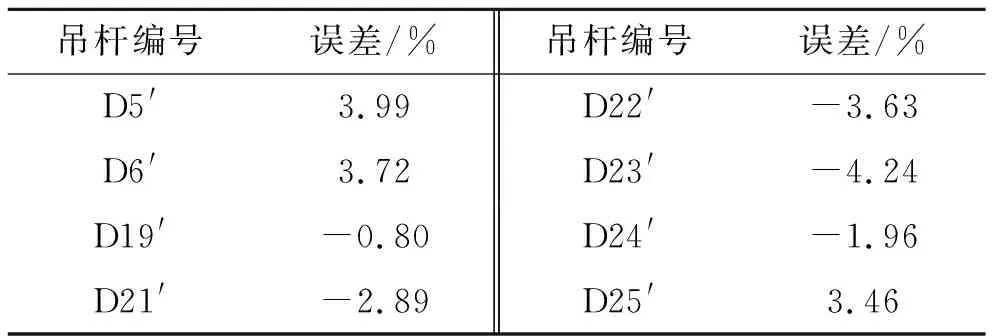
表2 推导公式计算误差

4 结论

从频率法基本原理出发，根据现有频率法测定索力过程中普遍存在的问题，推导出了考虑抗弯刚度但又不含抗弯刚度的索力计算公式，合理选择吊杆计算长度，结合工程实例中索力动测仪与油压千斤顶法实测结果误差分析，得出以下结论：

(1) 通过取边吊杆全长与索长所引起的相对油泵标定误差分析，结果表明：当吊杆包含连接件长度的全长小于13.303 m时，吊杆计算长度可取索长，其他吊杆计算长度取包含连接件长度的全长可得到较为精确的结果。

(2) 基于推导的考虑抗弯刚度但不含抗弯刚度的索力计算公式能实现吊杆索力较为精确、快速的测定。