目前世界最大跨度波形钢腹板PC箱梁桥
——安威川大桥的设计特点
张建勋, 赵谙笛 编译
(1.郑州市交通规划勘察设计研究院,河南 郑州 450008;2.新疆建设职业技术学院)
1 概述
日本新名神(名古屋至神户)高速公路安威川特大桥位于大阪府茨木市的北部,横跨一级河道安威川和茨木-龟冈市县道。上行线(即左幅)采用8跨预应力混凝土箱梁桥(4孔波形钢腹板组合箱梁+4孔预应力混凝土组合箱梁);下行线(即右幅)采用5跨波形钢腹板预应力混凝土组合箱梁桥。左幅桥梁最大跨度179.0 m(图1),是目前世界上最大跨径的波形钢腹板预应力混凝土组合箱梁桥,其主梁最大高度为11.5 m,横断面图见图2。针对现有设计方法能否适用于如此高的波形钢腹板组合箱梁问题,设计组通过非线性有限元分析法和缩尺模型试验对波形钢腹板的抗剪承载力进行了测试。结果表明:现有设计方法具有一定适用性。波形钢腹板按两种悬臂方法施工:第一种方法适用于右幅P2墩,将节段长度划为6.4 m,使用特殊移动挂篮;第二种方法适用于标准段,将节段设置为4.8 m,采用波形钢腹板与底板混凝土共同受力的架设方法。
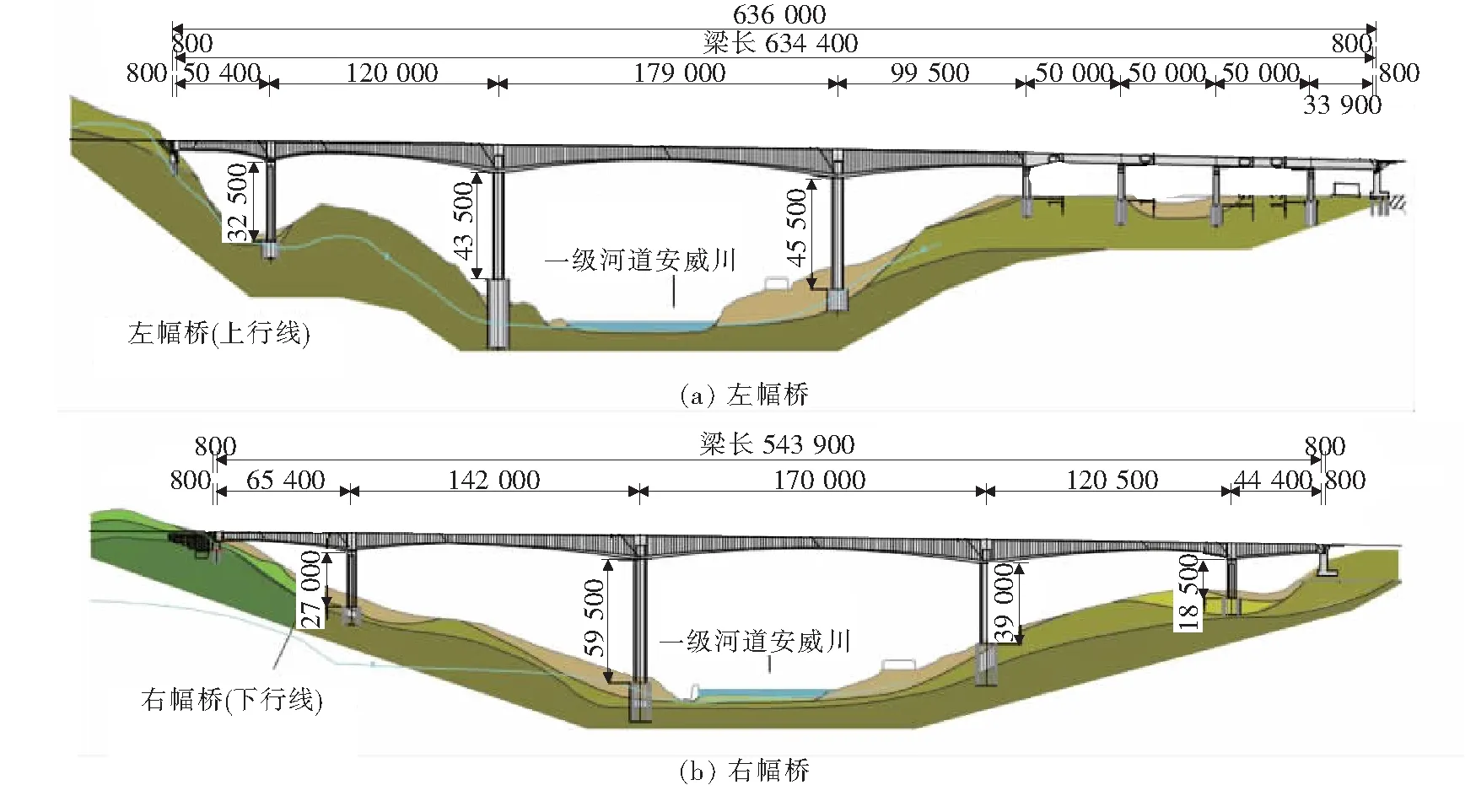
图1 桥梁立面图(单位:mm)
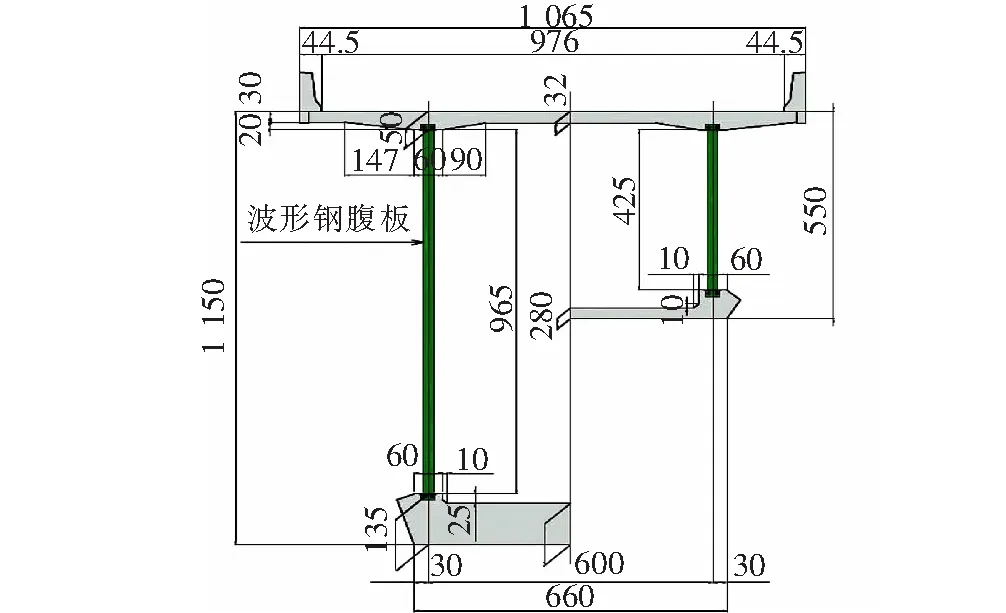
图2 桥梁横断面图(单位:cm)
2 截面剪切性能研究
2.1 数值分析结果与试验结果
通过非线性有限元分析和剪切屈曲试验,验证现有设计方案能否满足高梁波形钢腹板桥的受力要求。数值分析与试验结果的对比,如图3所示。试验载荷与挠度之间的关系与数值分析结果较为一致。以桥墩顶附近剪切屈曲参数约为1.0的非弹性区域梁段为试件,剪切屈曲强度的计算值和试验值分别约为现行设计方法屈曲强度的1.75倍和1.89倍,证明了此桥抗剪切屈曲的安全性。
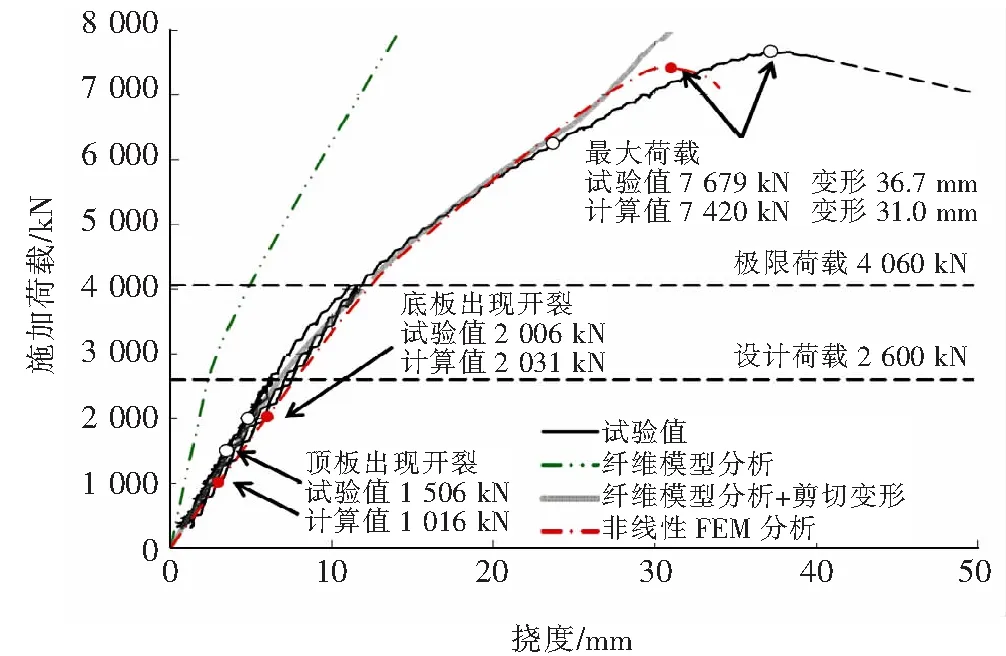
图3 数值分析与试验结果对比
2.2 波形钢腹板的设计方法
波形钢腹板桥梁设计通常假定由波形钢腹板承担横截面中的全部剪切力,设计应确保在极限载荷下不发生局部屈曲、整体屈曲和合成屈曲。其中,合成屈曲强度由局部屈曲强度和整体屈曲强度的相关指数之和表示。设计要确保每种剪切屈曲强度和剪切屈服应力均在安全范围内。剪切屈曲强度由弹性屈曲强度、剪切屈服应力和连接二者的非弹性屈服强度3部分组成,如图4所示。
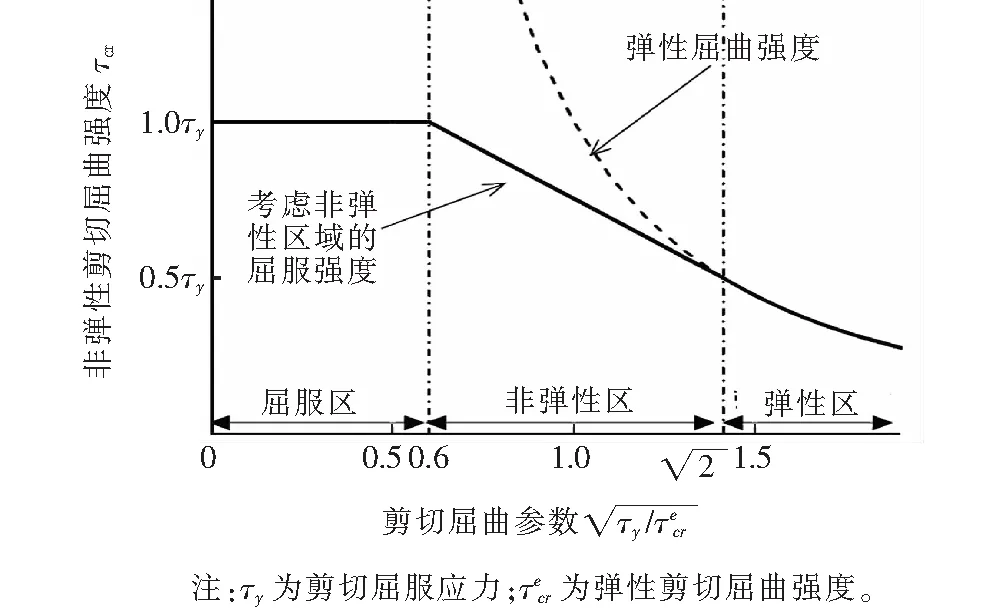
图4 剪切屈曲参数
2.3 波形钢腹板的结构设计
该桥波形钢板采用SM490Y和SM570两种钢材,考虑到经济性,采用变厚度钢板。支座中心剪力较小处使用SM490Y钢材;支座中心两侧剪力增大处使用SM570钢材。一般情况下,钢板厚度由非弹性区域屈服强度确定。为使钢板在非弹性区域优先屈服,剪切屈曲参数设置应小于1.0。经计算,在梁高11.5 m的墩顶附近,使用SM490Y和SM570两种钢材对应的板厚分别为25、42 mm,故该桥波形钢板选用SM490Y型钢材。
3 悬臂施工方法
3.1 悬臂施工方法的选取
该桥波纹钢腹板梁段采用两种悬臂施工方案进行施工。右幅P2墩各悬臂施工方案节段数量的对比见图5。传统的悬臂施工法将右幅P2墩悬臂梁节段分为20个。若采用4.8 m等节段标准施工法,将节段数由20个降至16个,可缩短施工时间;若采用6.4 m等节段的新施工法,可将右幅P2墩悬臂梁节段数从20个大幅降至12个,能进一步缩短工期。
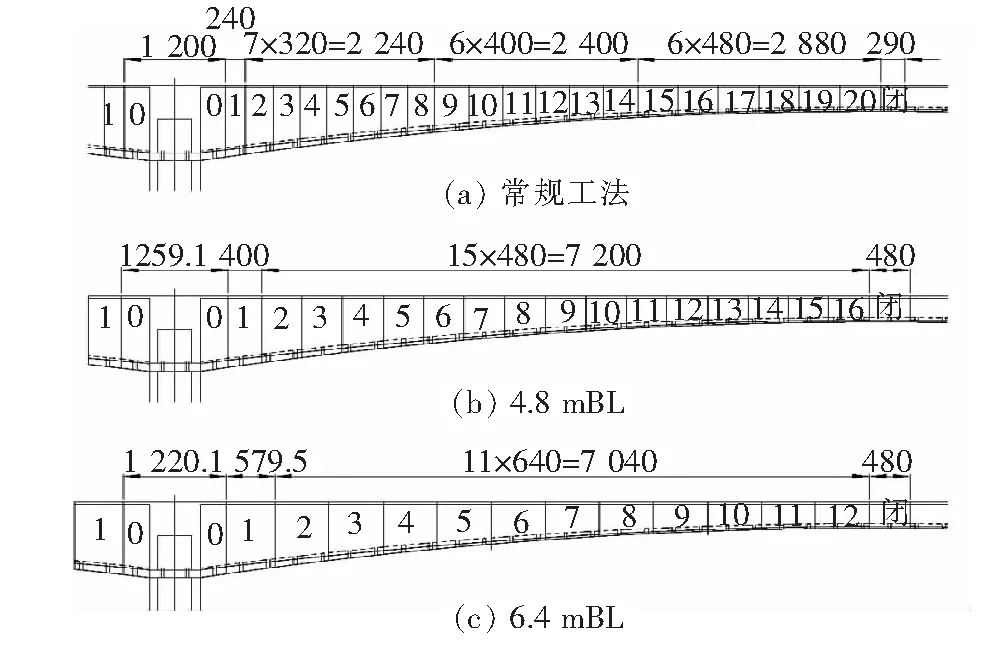
图5 右幅P2墩悬臂施工节段数量对比(单位:cm)
3.2 悬臂钢束设计
该桥的悬臂钢束由12束15.7 mm的高强度PC钢束组成。在悬臂法施工中,波型钢腹板的抗剪承载力是控制因素。为提高腹板刚度,需在波形钢腹板内侧增设内衬混凝土,由此,钢束的用量也将增加。随着主桥跨度的增加,悬臂钢束在顶板中的布置成了问题。如图6所示,普通强度PC钢(12束15.2 mm)无法全部布置于顶板中,故应采用高强度的PC钢材(12束15.7 mm)以减少钢束数量,确保钢束有足够的布置空间。
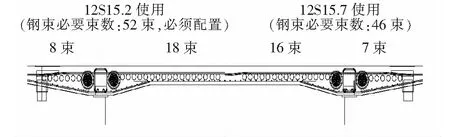
图6 体内钢束布置
3.3 标准节段(4.8 m)施工方法
顶板混凝土荷载由挂篮承担,底板混凝土荷载则由波形钢腹板承担。因挂篮不需要承受底板混凝土的重量,于是结构受力变得简单,从而可以将节段定为4.8 m的等长段,实现快速施工。底板混凝土荷载由通过螺栓和波纹钢腹板连接并安装在波形钢腹板上的支架承担,经有限元分析,支架应安装于距底板边缘1.5 m处。
3.4 长节段(6.4 m)快速施工方法
图7为右幅P2墩悬臂施工步骤:先将挂篮移动至提前安装好的波形钢腹板上,并通过挂篮安装后一节段波形钢腹板,然后在挂篮上浇筑6.4 m长节段的顶、底板混凝土,张拉钢束后,挂篮前移进入下一循环。该方法是该桥采用的第一种施工方法。由于简化了挂篮构造,挂篮尺寸得以增大,节段长度也可以延长至6.4 m。这样既能减少节段数量(与4.8 m节段划分相比,减少了4个块段),又大大缩短了施工工期。
采用新的施工方法后,需在每个节段的顶板内增加2束12φs15.7 mm的悬臂钢束。由于采用体内钢束,顶板加肋处的构造应相应改变,见图8。
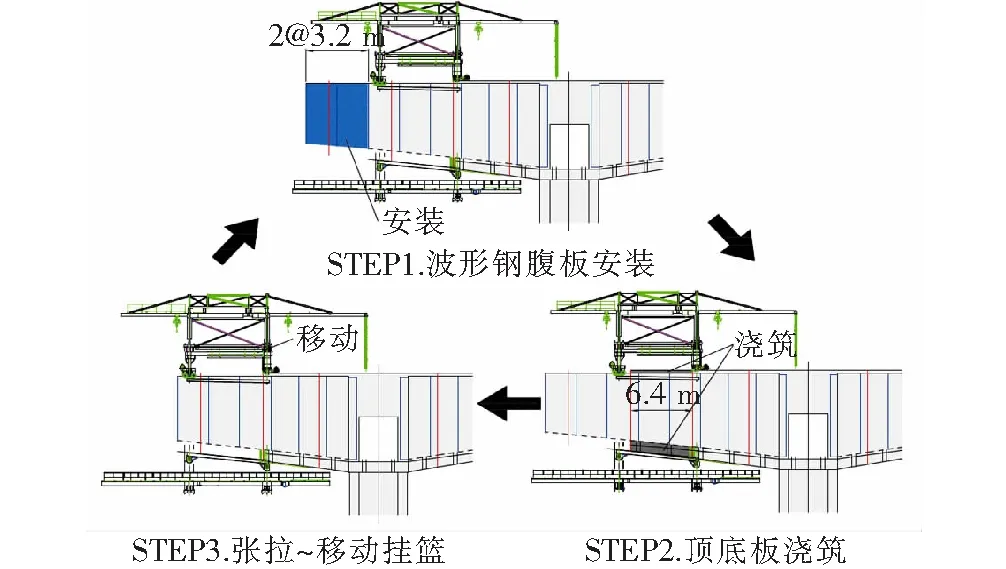
图7 新方法施工步骤图
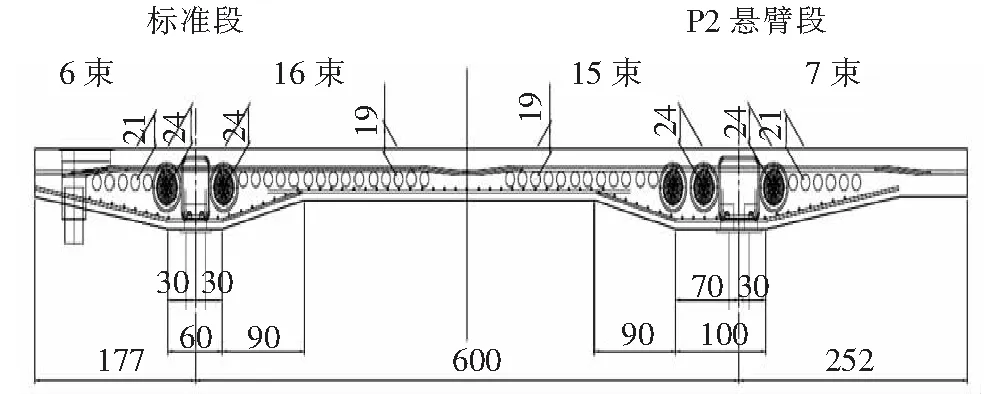
图8 右幅P2墩处与其他梁段顶板对比图(单位:cm)
另外,为了将高强度PC钢束集中锚固在顶板中,研究组对该位置进行了三维有限元分析,同时,通过对钢束锚固面进行钢筋补强控制结构拉应力。
在波形钢腹板的上翼缘处设置连接件,移动挂篮的前轮则放置于连接件上。连接件除作挂篮导轨外,还能承担挂篮的荷载和浇筑混凝土的荷载。
4 设计关键点研究
4.1 扭转性能研究
该桥中,波形钢板的高度已大于腹板间距,受偏载作用下扭转力矩的影响,活荷载可能会产生翘曲应力。为减小结构的扭转效应,行之有效的方法是增加横隔板。设计组试图通过有限元分析,确定横隔板数量并验证结构的抗扭安全性;选取跨度为179 m的单侧悬臂梁段进行建模分析,在横截面上施加活荷载(考虑偏载工况),并比较了结构在无隔板(方案1)、3道横隔板(方案2)和4道横隔板(方案3)3种工况下的断面变形情况,结果如图9所示。
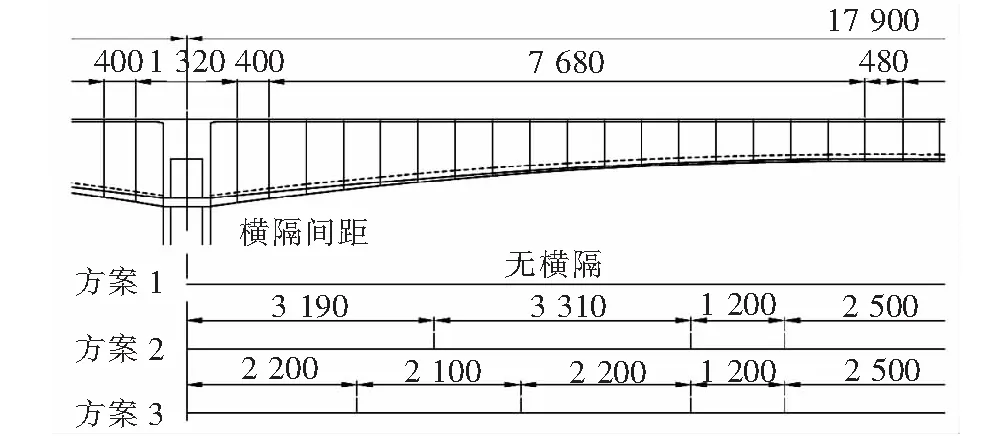
图9 横隔板方案对比研究(单位:cm)
在无横隔板情况下,波形钢腹板产生了弯曲应力,发生了面外变形。设置横隔板后,波形钢腹板产生的应力和变形均降低。由于翘曲应力的大小主要取决于有无横隔板,而横隔板布置数量的多少对翘曲应力的影响较小(0.2~0.4 MPa),考虑到桥梁的自重不应过大,综上所述,设计组采用了方案2:设置3道横隔板,不同方案的横断面变形如图10所示。
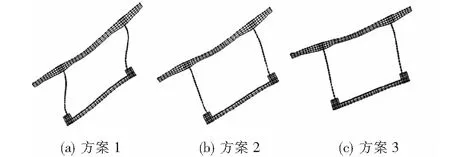
图10 横断面变形(活荷载下)
4.2 悬臂施工的横向屈曲研究
该桥主梁高度大且悬臂较长,悬臂施工时,存在横向变形的风险。因此,采用非线性有限元分析方法,验证了横隔板在施工前的横向抗屈曲性能的安全性。
设计组以桥梁实际的腹板厚度和钢板类型为参数,将左幅P6墩右侧最大悬臂状态下的梁段作为对象,进行了建模分析(图11)。初始荷载包括结构自身重力、悬臂状态下的预应力荷载、挂篮荷载和风荷载,见表1。
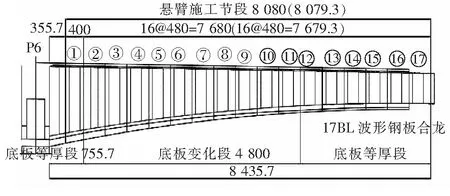
图11 分析模型(侧面图)(单位:cm)
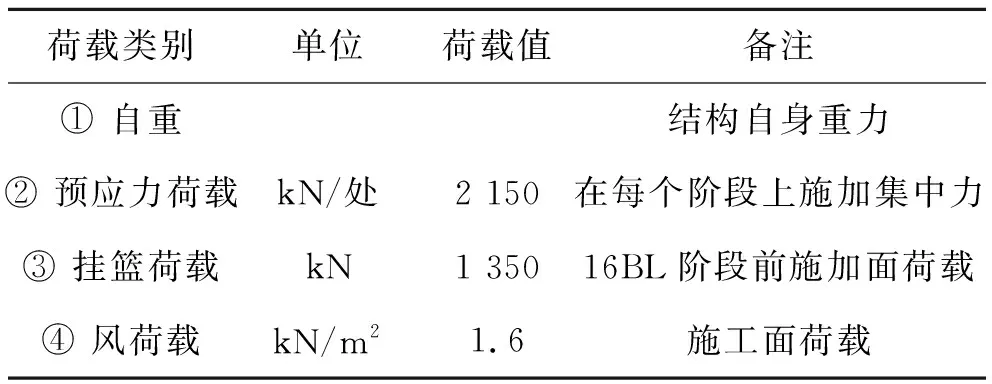
表1 荷载工况
为验证悬臂施工期间结构的横向屈曲状态,设计组分析了在初始载荷的基础上,分别逐级增加垂直荷载和横向荷载两种工况(表2)。结果表明:当垂直荷载约为自重和挂篮重量之和的4.4倍、横向荷载约为设计风速的8.8倍时(风速约为350 m/s),波形钢腹板均未发生横向屈服。由此确定,悬臂施工期间,即使没有横隔板,结构也足够安全。
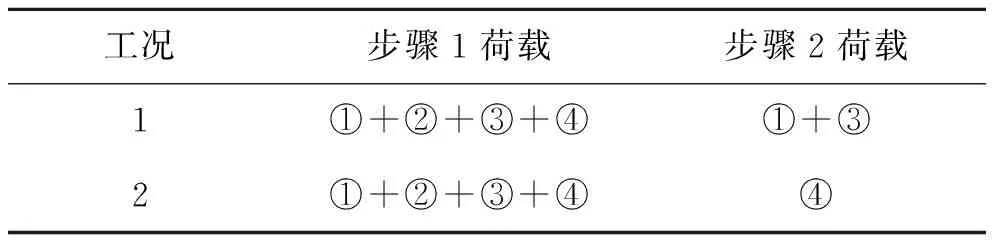
表2 加载步骤
5 结语
安威川大桥是目前世界上最大的波形钢腹板箱梁桥,其跨度和主梁高度在同类型桥梁中均居世界第一。因此,在设计阶段,该桥在施工和使用期的安全性问题就已经过充分考量。新的快速施工法能为未来的施工方案提供更多选择,该文可为今后同类型桥梁的设计和施工提供参考和借鉴。

