基于能量损失率最小原理求解稳定渗流场渗透系数

赵 磊，刘俊伟，刘冠杰

(烟台大学 土木工程学院， 山东 烟台 264005)

我国基坑工程和地下工程的建设规模和难度不断增大，其相关技术取得了长足的进步[1]，大基坑、深基坑层出不穷，但也发生了一些深基坑的工程事故。唐业清[3]对103项深基坑工程事故进行调查并分析了其原因，其中因为地下水处理(包含止水、降水、排水等)不当导致工程事故的案例有22项，占被调查总数的21.4%；杨子胜等[4]对大量深基坑工程事故资料进行了整理分析，总结出常见的导致基坑工程事故的因素，其中防水、降排水措施不当是事故发生的重要原因之一；周红波等[5]搜集了52例基坑事故资料，从工程风险的角度对这些案例进行分析归纳，总结出渗流破坏是该52起事故发生的主要因素，占比为62%。由此得出地下水控制是保障基坑工程安全的重要措施。

在基坑工程的建设中，地下水控制是十分重要的环节。目前，工程中基坑降水是普遍使用且经济有效的地下水控制措施，目的是为后续基坑工程的建设提供干燥且安全的施工环境。其中，对于降水区域渗流参数的求解是一个关键的环节。

常安定等[6]通过分析割离井法的井流函数性质，简化井流函数，将直线图解法引入割离井法中反求水文地质参数，但该方法未考虑水跃值对渗流场参数的影响；刘天霸等[7]将最频值算法与Jacob直线图解法耦合得出一种新的直线图解法，并将其运用到了用抽水试验获取含水层水文地质参数的思路上，但该方法仅在试验区进行验证，并没有实际工程案例的数据作为对比。

在实际工程中，渗透系数[8]的确定往往需要进行现场抽水试验，增加了时间成本以及工程造价。本文提出了一种计算稳定渗流场渗透系数的有限单元方法。该方法无需进行现场抽水试验，并考虑了水跃现象[9-11]的影响，基于能量损失率最小原理[12-14]计算潜水含水层的渗透系数。采用该方法计算了两个工程案例，求得了两个基坑渗流区域的渗透系数，并与实测值进行对比，结果表明本文方法具有较高精度，对其渗流场的分析与降水工程的设计有指导意义。

1 基本理论

由变分原理可知，渗流场基本微分方程的定解问题等价于求解渗流能量泛函的极值问题，构造如下泛函：

(1)

[K]{h}={f}

(2)

式中：[K]为总渗透矩阵；{h}为待求节点的水头向量；{f}为自由项。

2 稳定渗流场的渗透系数的计算方法

2.1 建立稳定渗流场模型

稳定渗流场由上游水头、下游水头、降水影响半径、下游逸出段以及降落曲线组成，据此建立图1所示的均质潜水完整井二维稳定渗流场剖面示意图。

图1 均质潜水完整井的二维稳定渗流场剖面示意图

图中A点为降水前地下水位点，AO段为渗流场影响半径R，E点为地下水实际逸出点，DE段为实际逸出点与降水井水位之间的出渗段，可将其看作下游逸出段[15-17]，D点为降水井水位点，AB段为潜水含水层厚度。

降水影响半径R可根据《建筑基坑支护技术规程》中给定的经验公式确定。在经验公式中，R与降水井降深sw、渗透系数k以及潜水含水层厚度H有关。在实际工程中，sw和H已知，R的大小直接取决于k的取值。

下游逸出段位于降水实际逸出点与井中水位之间，是一种当降水井水位降深较大时，出现的降水井水位低于井壁水位的现象，逸出段大小可由水跃值表示，水跃值可由阿布拉莫夫经验公式[18]确定：

(3)

式中：q为单井排水量,m3/d；F为过滤器工作部分表面积,m2；α为与过滤器构造、阻力有关的系数。

水跃值确定后，实际逸出点E点高度可由下式确定：

sd=b+Δh

(4)

根据图1所示的均质潜水完整井二维稳定渗流场剖面示意图建立图2所示的有限元计算模型。A1B1段赋予上游边界水头；C1D1段赋予下游边界水头；B1C1、A1G1、G1E1赋予不透水边界条件；D1E赋予逸出边界条件。

当已知稳定渗流场的上下游水头以及实际逸出点位置时，可基于能量损失率最小原理求解渗流场渗透系数。以下游水头位置水平往右一点O为坐标原点，建立图3所示的计算模型，图3(a)横轴代表不同逸出点计算出的能量损失率数值，图3(b)横轴代表渗透系数数值，两图纵轴均代表不同逸出点位置。

图2 均质潜水完整井的二维稳定渗流场有限元计算模型

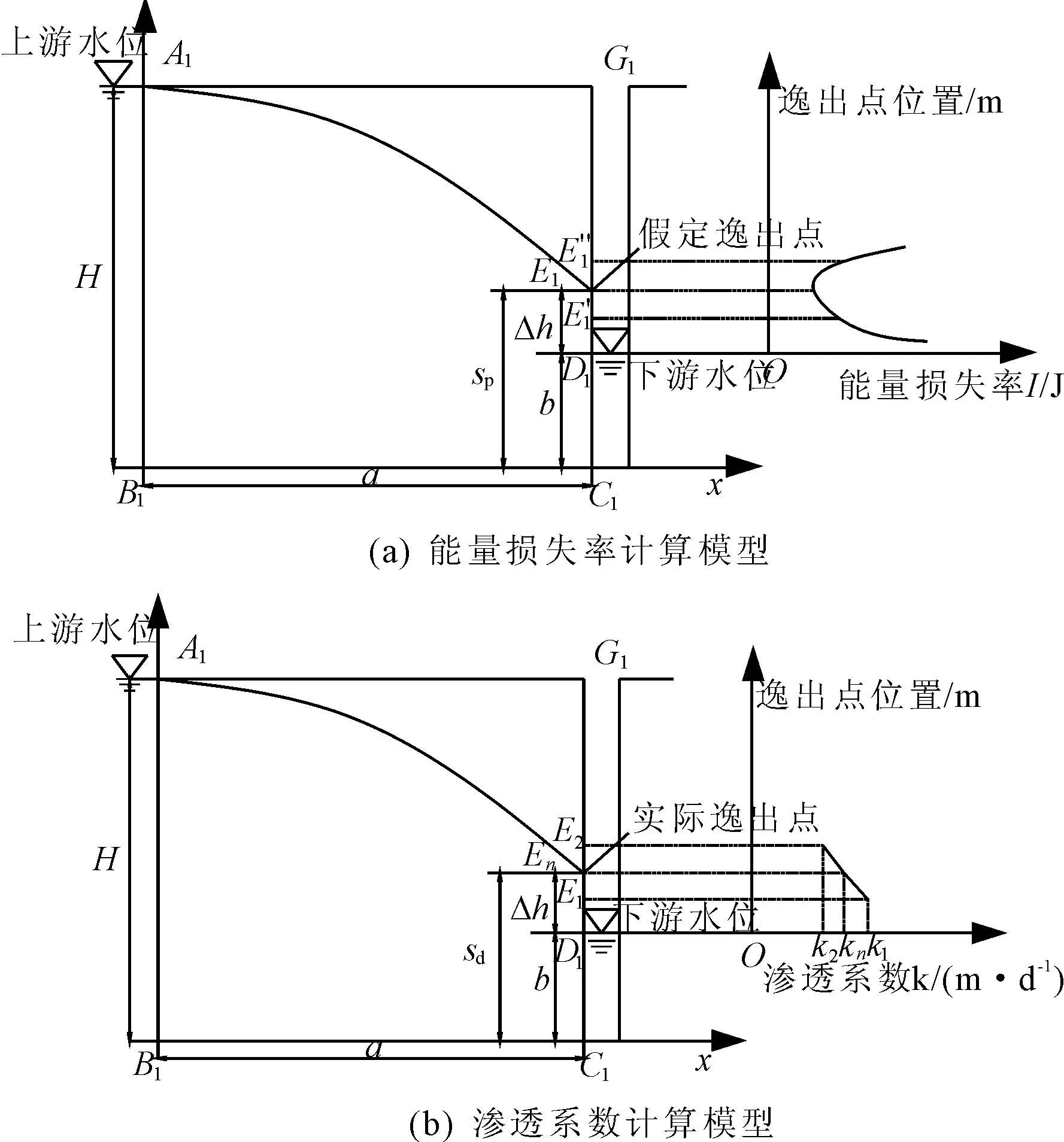
图3 渗透系数计算模型

2.2 计算步骤

根据能量损失率最小原理，编制Fortran程序，求解稳定渗流场中渗透系数，程序框图如图4所示，具体计算步骤如下：

(1) 假定一渗透系数k1，由经验公式可得影响半径R1，结合潜水含水层厚度H，确定稳定渗流场的横向尺寸和纵向尺寸。

(2) 由式(3)的阿布拉莫夫经验公式确定水跃值，式(4)确定渗流实际逸出点E。

(3) 将稳定渗流场进行有限单元划分，以三角形六节点为例，对单元和节点进行编号。读入单元节点信息、土层信息参数以及边界条件。

(4) 读入土层信息参数，基于能量损失率最小原理确定逸出点的位置E1。

(5) 若E1≠E′，则调整步骤(1)的渗透系数及影响半径，重复步骤(2)—步骤(4)，直至在渗透系数kn下求解出的逸出点位置En≠E′，此时的kn即为该稳定渗流场真实的渗透系数。

图4 有限元计算程序流程

3 工程实例

3.1 某市正海广场工程场区渗流参数计算

拟建某市正海广场工程场区位于该市开发区衡山路与珠江路交叉口处，基坑周长约462.0 m，开挖区域约14 135.0 m2，深度9.1 m～9.6 m。根据勘察，拟建场区地下水类型为孔隙潜水，含水层主要为粉细砂层、粉土层，厚度为12.0 m。静止地下水位在地面以下1.98 m处，实际降水井水位降深为8.65 m，由式(3)计算得水跃值Δh=2.52 m，实际逸出点位置为5.87 m，建立图5所示计算模型。

图5 案例1渗流场剖面及计算模型

采用本文2.2节介绍方法计算该渗流场渗流参数。将该渗流场剖分为图6所示的800个三角形六节点单元。

图6 计算模型网格划分

依据图4的计算流程，基于能量损失率最小原理先计算该稳定渗流场的渗透系数。本文方法计算的渗透系数与实测渗透系数对比情况如表1所示，本文方法计算的渗透系数k为10.8 m/d，与现场实测值相比绝对误差为0.47 m/d，相对误差为-4.17%，具有较高的精度。

表1 案例1渗透系数精度对比

3.2 西安地铁北客站工程场区渗流参数计算

西安地铁北客站位于西安市北部郊区，地处渭河平原，地势平坦。该场地主要含水层为第四系冲积砂孔隙潜水含水层，主要土层是中粗砂层，厚度为23 m。

该工程基坑面积约为36 600 m2，深度为19.2 m，为保证施工安全，场地地下水水位应降至基坑底下部1.0 m处。静止地下水位在地面以下12.0 m处，实际降水井水位降深为8.2 m，由式(3)计算得水跃值Δh=2.21 m，实际逸出点位置为17.01 m，由已知条件建立稳定渗流场渗流参数计算[19]模型，如图7所示。

图7 案例2渗流场剖面及计算模型

采用本文2.2节介绍方法计算该渗流场渗流参数。将该渗流场剖分为图8所示的800个三角形六节点单元。

图8 计算模型网格划分

依据图4的计算流程，基于能量损失率最小原理先计算该稳定渗流场的渗透系数。本文方法计算的渗透系数与实测渗透系数对比情况如表2所示，本文方法计算的渗透系数k为24.1 m/d，与现场实测值相比绝对误差为0.8 m/d，相对误差为-3.5%，具有较高的精度。

表2 案例2渗透系数精度对比

4 结 论

(1) 为了能更精准的确定基坑降水工程中渗流区域的渗透系数，节约时间成本和工程造价，本文提出了一种计算稳定渗流场渗透系数的有限单元方法。该方法无需进行现场抽水试验，并考虑了水跃现象的影响，基于能量损失率最小原理计算潜水含水层的渗透系数。

(2) 研究了稳定渗流场渗透系数有限元数值计算方法的步骤，利用Fortran编制了一套二维有限元数值计算程序。

(3) 采用该方法计算了两个工程案例，求得了两个案例渗流区域的渗透系数，并与实测值进行对比，结果表明本文方法具有较高精度，对渗流场的分析与降水工程的设计有指导意义。