橡胶连杆的几何参数对机构动力学的影响分析

程寿国，苏春芳

橡胶材料作为一种非线性材料，其减振隔震非线性动力学问题一直备受关注［1-3］.SYED 等学者利用高频动态力学分析仪测量原始信号，对橡胶材料的非线性响应进行了分析［4］.安林等结合实验和有限元法研究了炭黑填充橡胶在加载情况下的温度变化和应力软化问题［5］.程寿国等考虑了橡胶材料构件的柔性、曲柄转速、铰链接处轴承外径尺寸等因素对曲柄滑块机构运动的影响，并分析了机构运动的稳定性［6］.

众所周知，橡胶材料构件在力的作用下产生大变形，而不同截面形状的橡胶材料连杆在匀速曲柄作用下发生怎样的变形，以及它的变形对与之相连接的滑块动力学响应有何影响，是本文研究的主要内容.

1 含橡胶连杆的曲柄滑块机构简介

为了表述方便，在连杆的两个铰孔中心距不变的情况，改变连杆的形状尺寸.橡胶连杆的基本几何参数见图1，连杆的两个铰孔中心距320 mm，厚度20 mm，图中定义了两个尺寸参数a和b.根据a、b值的大小和材料是否是柔性体定义四种情况：

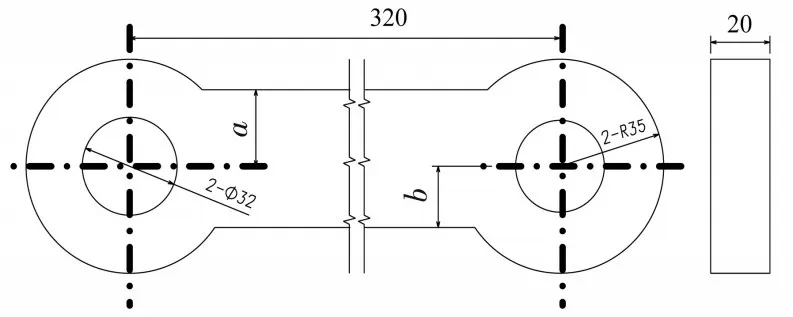
图1 橡胶连杆的基本几何参数图

condition 1：全刚体模型，a=b=25 mm.

condition 2：连杆为橡胶材料的柔性体，a=b=25 mm.

condition 3：连杆为橡胶材料的柔性体，a=20 mm，b=25 mm.

condition 4：连杆为橡胶材料的柔性体，a=25 mm，b=20 mm.

对后面的三种情况分别利用NASTRAN 求解器做有限元仿真，生成*.mnf 文件，在利用SIMDESIGNER 软件做动力学仿真时激活柔性体作刚柔耦合分析.

2 仿真结果分析

仿真时曲柄以5 r/s 的速度转动.机构初始情况下，a=b=25 mm，全刚体模型（condition 1）仿真计算时不激活柔性体.在condition 2 条件下，激活橡胶材料连杆为柔性体.在condition 3和condition 4 条件下，先修改连杆尺寸，重新生成柔性体并在仿真时激活连杆为柔性体.

滑块动力学响应见图2.图2（a）为滑块在两个周期内的位移变化图，从图中可以看出，考虑橡胶材料为柔性体时，滑块位移曲线中位移都比全刚体情况大得多，比较四种条件下滑块的位移曲线可知，当考虑橡胶连杆柔性时，连杆两轴承孔的孔距在曲柄转动时被动态拉长，即连杆的有效长度被拉长，滑块的位移大于曲柄长度的两倍，在波峰和波谷之间也会出现一些小的波动.condition 2 比condition 3 和condition 4 的波峰值（例如在曲柄转到427°附近）更大一些，也就是说柔性连杆为对称结构时变形量更大一些.当曲柄转到183°、367°和550°附近时出现了小的波峰和波谷，这也是曲柄转动时对柔性连杆的作用力所导致的.同时还发现柔性橡胶材料后整个位移图比全刚体条件下波峰和波谷更加陡峭.图2（b）为滑块在两个周期内的速度变化图.对比全刚体条件下，后三种情况下速度的波动更大一些.condition 2 比condition 3 和condition 4 在每一个波峰或者波谷到来的位置要提前一点，这与从图2（a）中得到的信息是一致的，而且condition 2 比condition 3 和condition 4的波峰或者波谷到来的时间差越来越大.虽然condition 3 和condition 4 的波峰或者波谷到来时间接近，但他们的波峰（或者波谷）的幅值差值逐渐增大，condition 3 和condition 4 条件下连杆的截面积相同但结构分布不同，所以使得受力后变形量不同，滑块的速度随之改变.图2（c）为滑块在两个周期内的加速度变化图.比较condition 2、condition 3 和condition 4 可以发现，condition 2 中波峰或者波谷到来位置要提前一些.数值上，两种不对称结构（condition 3 和condition 4）比 较 接 近.从 图2（c）中可以看出，柔性橡胶材料的机构中滑块的加速度增添了很多频率成分.

图2 滑块动力学响应图

3 系统稳定性分析

相图观察法与计算最大Lyapunov 指数值是讨论系统稳定性常用的定性和定量分析方法.

3.1 相图观察法

在非线性系统稳定性讨论的判据中，相图观察是采用的最普遍的方法之一.图3 为滑块的速度与加速度相图，图3（a）、3（b）、3（c）分 别是condition 2、condition 3 和condition 4 与condition 1 的对比相图.condition 1 时机构构件为全刚体，所以相图为一封闭曲线，代表其为周期性运动.condition 2、condition 3 和condition 4三种情况考虑了橡胶连杆为柔性体，在运动过程中橡胶连杆受到曲柄拉压作用不断地发生变形，所以橡胶连杆为柔性体时（condition 2、condition 3 和condition 4）的相图与condition 1时的相图有很大差别.四种条件下滑块的位移、速度和加速度的相图如图4 所示.

从滑块的速度与加速度相图（图3）可以看出，两侧端点像两个“吸引子”，相图围绕在两个端点周围，这一点和其他典型的非线性系统非常相似.

从图4（a）和图4（c）的相图看出，condition 2、condition 3 和condition 4 三种条件下的相图都似乎有两个“吸引子”，相图曲线围绕着“吸引子”.图4（b）中condition 1 的相图是“一段”曲线，其他三种情况都是不重合的相轨迹，初步观察系统有可能是混沌的，需要通过其他非线性判据进一步研究.

图3 滑块的速度与加速度相图

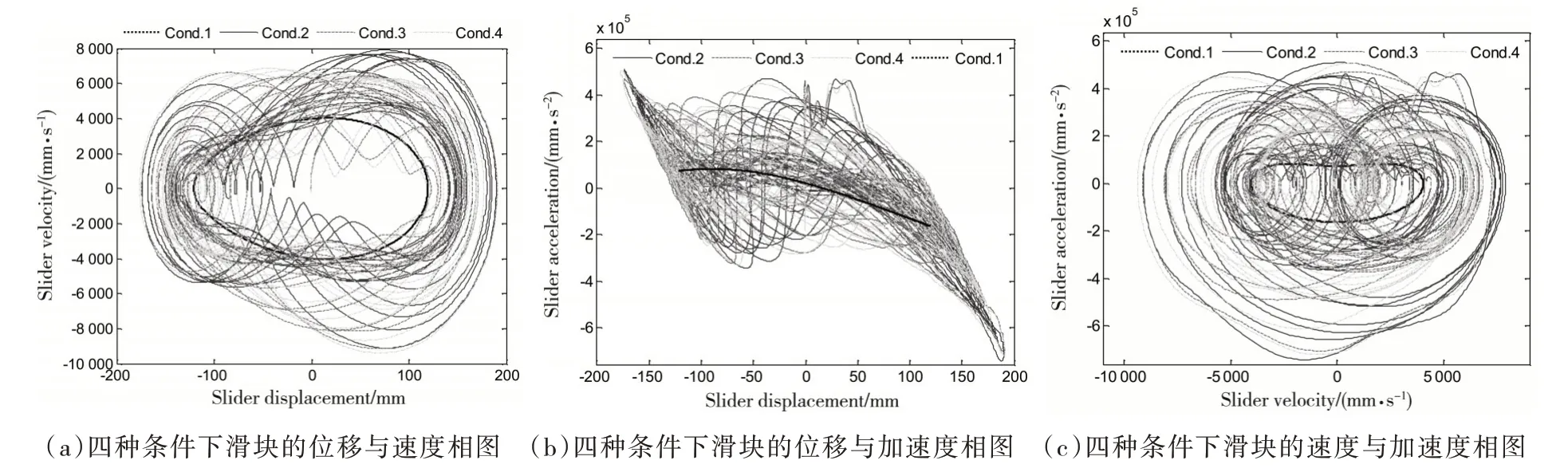
图4 四种条件下滑块在三个周期内的相图

3.2 计算最大Lyapunov 指数值

计算最大Lyapunov 指数值是定量分析系统运动稳定性常用的方法之一，如果计算最大Lyapunov 指数值为正，通常判定系统的运动是混沌的（有时需要几个判据一起考虑）.图5 为用WOLF 法计算的后三种情况下的Lyapunov 指数谱.condition 2、condition 3 和condition 4 等条件下计算的最大Lyapunov 指数值分别为0.020 7、0.014 9 和0.016 7.

图5 Lyapunov 指数谱

4 结论

通过对橡胶材料连杆进行有限元建模并生成柔性体，在机构做动力学仿真时激活柔性体进一步揭示含橡胶材料连杆的机构的动力学行为，通过全刚体机构分析与刚耦分析对比、对称连杆结构与非对称连杆机构对比来研究滑块的动力学响应.将非线性橡胶材料特性在机构运动中展现出来，为橡胶材料和复合材料在机构学中的应用打下基础.