基于机器视觉和卷积神经网络的轨道表面缺陷检测方法

姚宗伟，杨宏飞，胡际勇，黄秋萍，王 震，毕秋实

(1.吉林大学 机械与航空航天工程学院,吉林 长春 130025；2.数控装备可靠性教育部重点实验室,吉林 长春 130025；3.一汽-大众汽车有限公司，吉林 长春 130011)

高速铁路钢轨的质量是影响高铁列车运行安全的关键因素，实时准确检测轨道表面缺陷，对于及时排除轨道的潜在风险至关重要。轨道缺陷检测方法主要分为以下三类：一是人工应用工具敲打和裸眼目测的方法，具有较大的主观性；二是借助于激光[1]、超声波[2-3]、红外线[4]和涡流[5]等传感器的检测方法，此类方法对传感器本身的可靠性和精度要求较高；三是基于传统的图像处理和机器视觉方法[6]，此类方法的主要关注点在于异常对象的定位，其中图像处理过程占用了大量的计算时间[7]。

除此以外，随着计算机和信息技术的发展，出现了利用机器视觉和基于神经网络的检测方法[8-10]。该方法可以较好地降低检测人员的主观影响，文献[9]应用该方法对轨道表面质量进行了检测，但查准率和召回率不够高，距离实际应用相差较远。

本文提出一种基于机器视觉和卷积神经网络的轨道表面缺陷检测方法。首先应用灰度化、分割ROI(Region of Interest)、图像形态学变换以及概率霍夫变换等机器视觉方法对图像中的轨道进行智能识别；然后通过中值滤波[11]和双边滤波[12]剔除图像中的噪声信息，并结合Canny算法[13]，顺次应用阈值法和离散法去除伪边缘，提取轨道的真正边缘；最后，基于卷积神经网络建立高效的轨道表面形态分类器[14]，完成对轨道表面特征的自动提取，从而将轨道分成完好和有缺陷两类。轨道表面缺陷检测方法流程见图1。

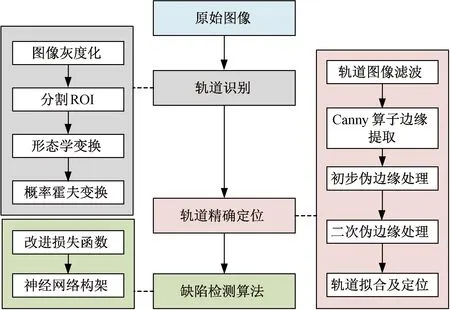
图1 轨道表面缺陷检测方法流程

1 轨道识别

在此部分，需要依次对图像进行灰度化、分割ROI、形态学变换和概率霍夫变换4个预处理步骤，具体流程见图2。

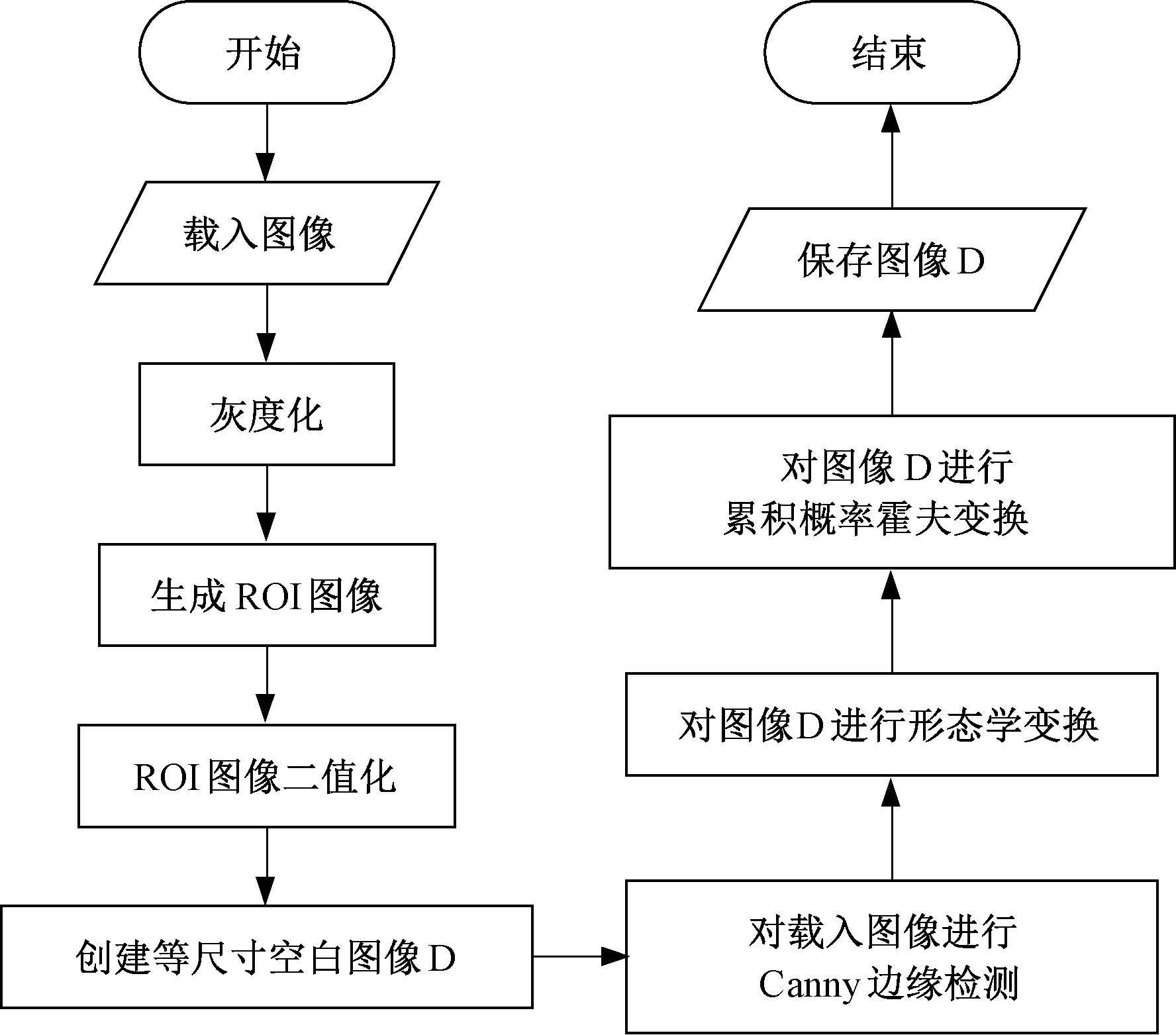
图2 轨道识别算法流程

1.1 图像灰度化分割ROI

采用灰度加权法，将原始RGB图像转化为易于识别的灰度图像。考虑到轨道和路基有较大色差，用矩形滑动检测窗口遍历，进行模板匹配，识别出ROI区域。在ROI区域，计算各像素点灰度的均值μf和方差σf，根据式(1)计算出分割阈值IT，以此为据对灰度图进行分割，得到二值图像。

IT=μf+3σf

(1)

将ROI区域分为左右两个部分，分别记为LD和RD。将LD和RD区域内的有效像素点分别按列放入集合D中，再进行后续的处理。

1.2 形态学变换和概率霍夫变换

为了消除噪声的影响以寻找图像中明显的极大值区域，应用形态学膨胀和腐蚀作差的方法进行处理。

(2)

(3)

(4)

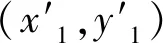
为了降低运算时间，采用概率霍夫变换方法，只需要操作平面内部分点即可完成检测。

1.3 轨道识别结果

分别采用经典霍夫变换和结合形态学滤波的改进霍夫变换的方法对轨道进行识别，轨道识别精度与用时对比如表1所示，对轨道进行识别的结果见图3。在所有识别的8 523张轨道图像中，识别轨道的轨迹与人工标记相同为正确识别，经典霍夫变换方法正确识别到8 152张轨道图像，改进霍夫变换正确识别到8 431张轨道图像。根据轨道识别结果，经典霍夫变换精度为95.65%，10次识别平均时间为131 ms；而采用改进霍夫变换相结合的方法精度为98.92%，10次识别平均时间为25 ms。

表1 两种方法精度、用时对比

图3 轨道识别

2 轨道的精确定位

经过前文的处理，已经识别到了图像中的轨道，但还需要进行精确定位。

2.1 轨道图像滤波和Canny算子边缘提取

首先采用中值滤波，再进行双边滤波，消除图像中的噪声，经过Canny算法对边缘进行检测。轨道原图及其顺次处理结果见图4，轨道原图像见图4(a)，边缘检测后的结果见图4(b)。可以看到，检测的结果包含了大量伪边缘，需要进行伪边缘处理。

图4 轨道原图及其顺次处理结果

2.2 伪边缘初步处理

对轨道位置进行检测，若检测到轨道垂直放置，则对像素值矩形进行转置处理；若检测到轨道水平放置，则不进行处理。

伪边缘初步处理，将待检测图像第i行像素进行加和得到Si，然后将Si与阈值ST进行比较，如果Si>ST则保留为边缘，否则跳过，进行第i+1行像素的加和、比较，直到找到满足条件的像素行，并将其所在行数记为L1，作为轨道的一侧边缘界限。同理，可以找到轨道另外一侧的边缘界限L2。此算法关键在于阈值ST的选择上，其值会直接影响算法的效果和分割的准确性。经过大量试验，提取效果较好的阈值ST为

(5)

式中：n为图像总列数；Imax为最大像素值；Is为像素缩小倍数，取Is=5。

伪边缘初步去除程序流程见图5。

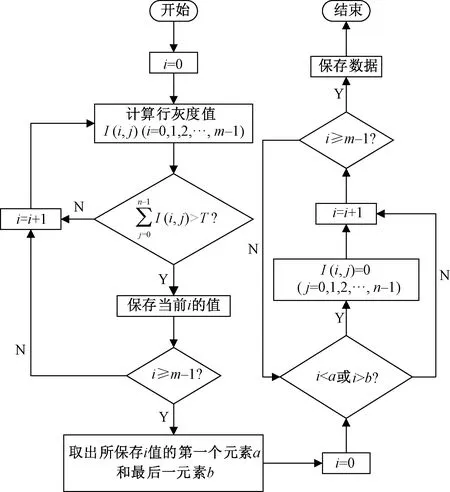
图5 伪边缘初步去除程序流程

此时得到的边缘并不仅有L1和L2两条，只是初步去除了Canny算法检测得到的一些具有较大偏差的伪边缘。伪边缘初步处理效果见图4(c)。

2.3 伪边缘二次处理

由图4(c)可知，图像中连续性最好的两条边缘为真正的边缘，其各像素点的像素值与算术平均数的差异程度较小；其他各像素点的像素值跳跃性较大为伪边缘。因此，应用每条边缘的离散程度判断其是否为伪边缘，取其中标准差最小的两条作为真正的边缘保留，其他作为伪边缘去除。根据以上分析，应用约束条件式(6)对伪边缘进行去除。

(6)

式中：STDi为轨道图像第i行的像素值标准差，i=0,1,2,…,m-1；n为输入图像的总列数；m为输入图像的总行数；c为可以调整的动态因子，其对结果的影响将在试验部分给出。伪边缘二次去除效果见图4(d)。

2.4 轨道拟合及定位

由于除去伪边缘的操作可能对真实边缘造成影响，从而需要进一步恢复。将伪边缘清理后保留下的两组边缘点进行线性拟合，得到两直线的截距和斜率后可以近似恢复实际边缘。边缘拟合结果见图4(e)，轨道最终定位结果见图4(f)。

3 缺陷检测算法

经上文处理已经得到了轨道的精确图像，可以输入到卷积神经网络中进行模型训练。

3.1 构建交叉熵函数

由于铁路安全的特殊性对查准率和召回率的要求有别于其他案例，所以需要定义一个能用于权衡查准率和召回率的损失函数。

在机器学习中，一般根据查准率P和召回率R来评价检测与识别效果，应用交叉熵代价函数C(r)来衡量神经网络预测值与实际值的接近程度以促进模型的训练，其定义分别如式(7)～式(9)所示。

(7)

(8)

(9)

式中：TP为准确检测出的缺陷轨道数量；FP为错误检测出的缺陷轨道数量(即实际为完好轨道却错误检测为缺陷轨道)；FN为实际为缺陷轨道却检测为完好轨道的数量；M为样本总数；yr为样本r的实际值；y(r)为样本r的预测值。

由于在常规卷积神经网络应用的交叉熵代价函数与召回率没有直接关系，所以引入变量K(r)来平衡查准率和召回率，以满足轨道缺陷检测的特殊要求。K(r)的定义为

(10)

式中：ω为权重，其对结果的影响将在试验部分进行具体分析。

由于训练期间的当前样本的参数对现阶段的结果影响最大，所以需要关注其变化趋势。用t和s分别表示中间迭代次数和当前迭代次数，当前样本的查准率和召回率可表示为

(11)

(12)

为了便于后续的计算,将变量K(r)和交叉熵C(r)进行均值标准化[10]

(13)

(14)

式中：μK、σK为K(r)的平均值和方差；μC、σC为交叉熵函数C(r)的平均值和方差。进一步，提出新的代价函数为

(15)

从式(15)可以看出，变量K(r)对查准率、召回率和损失函数都有比较强的约束，可以使分类器向最优化的方向运行。

3.2 卷积神经网络结构

建立Orbitcnn网络进行轨道表面分类，Orbitcnn网络[15]结构见图6。该网络由47层网络构成，可将大卷积核分解为几个小卷积核，包含11个Inception-v3原始模型[16]和96个并行卷积层，并将原Inception-v3网络的第3个池化层后的最终层替换为2个神经元。较早层采用5个模块A，见图7，主要将一些较大的卷积核分解成几个较小的卷积，比如可将5×5的卷积分解为两个3×3的卷积，参数量减少了28%，但是两者感受野是等价的，中间层是采用4个模块B，图8是将n×n的卷积分解成1×n和n×1卷积，同样地这种分解在保证相同效果下降低了参数量。后面层采用了2个模块C，见图9，其特点是卷积组被扩展以产生更多不一样的特征，为了防止直接使用max pool层进行采样从而导致信息损失较大，该网络采用一个池化层和一个卷积层[17]，最后将两者的结果连接在一起，这样可以防止特性数量的减少，从而在较小的计算量情形下避免瓶颈层。

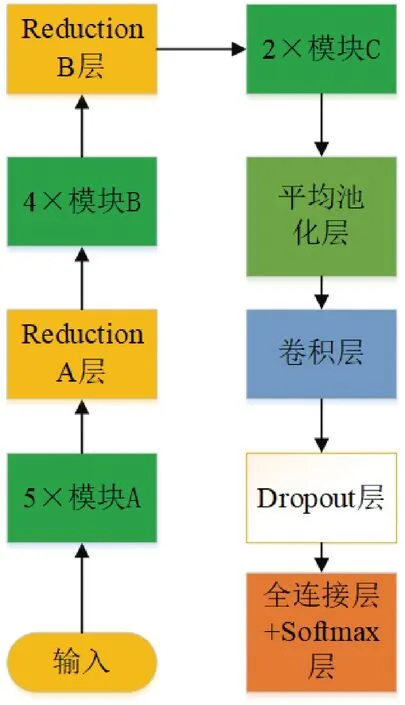
图6 Orbitcnn网络结构

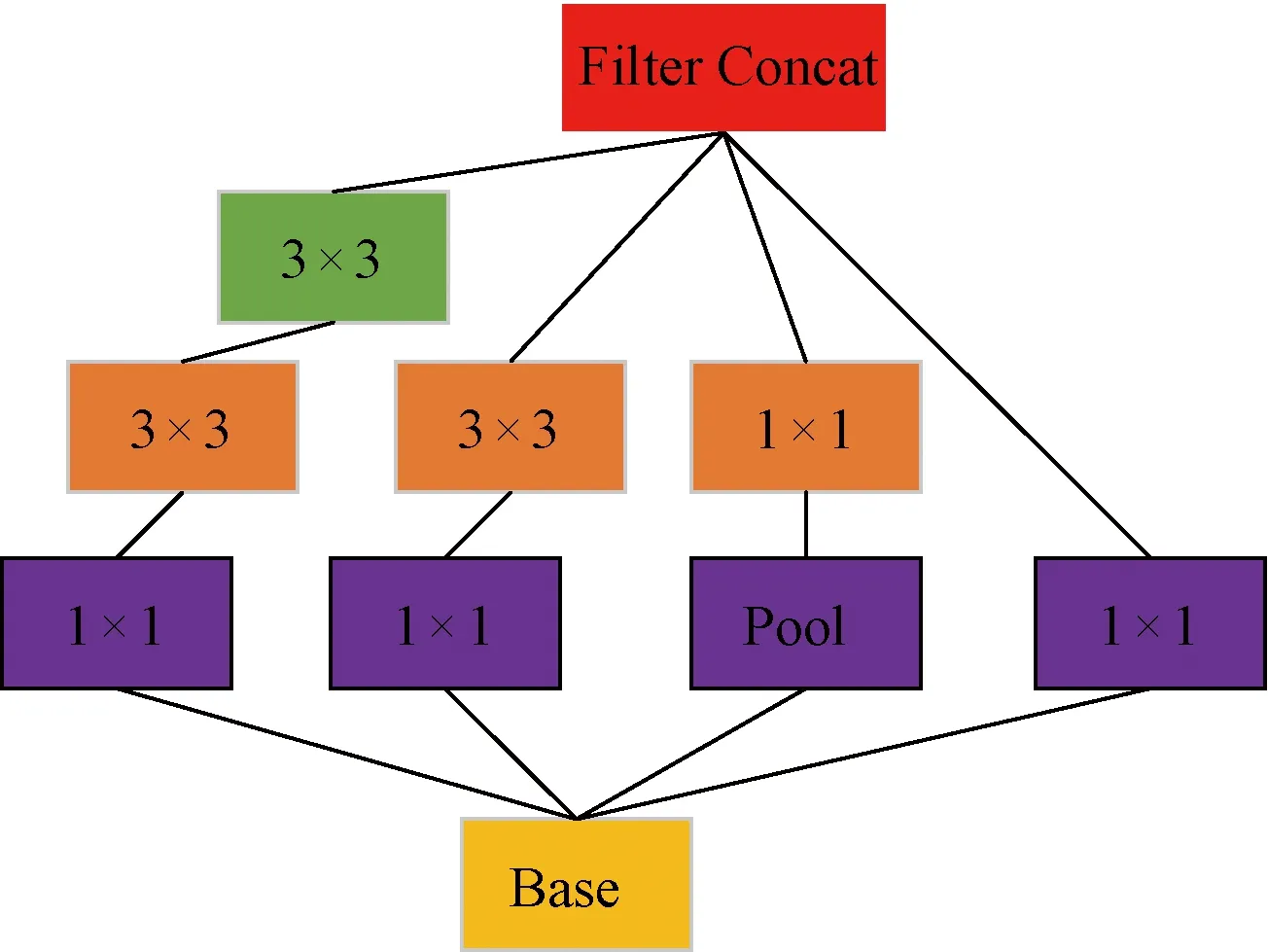
图7 模块A

图8 模块B

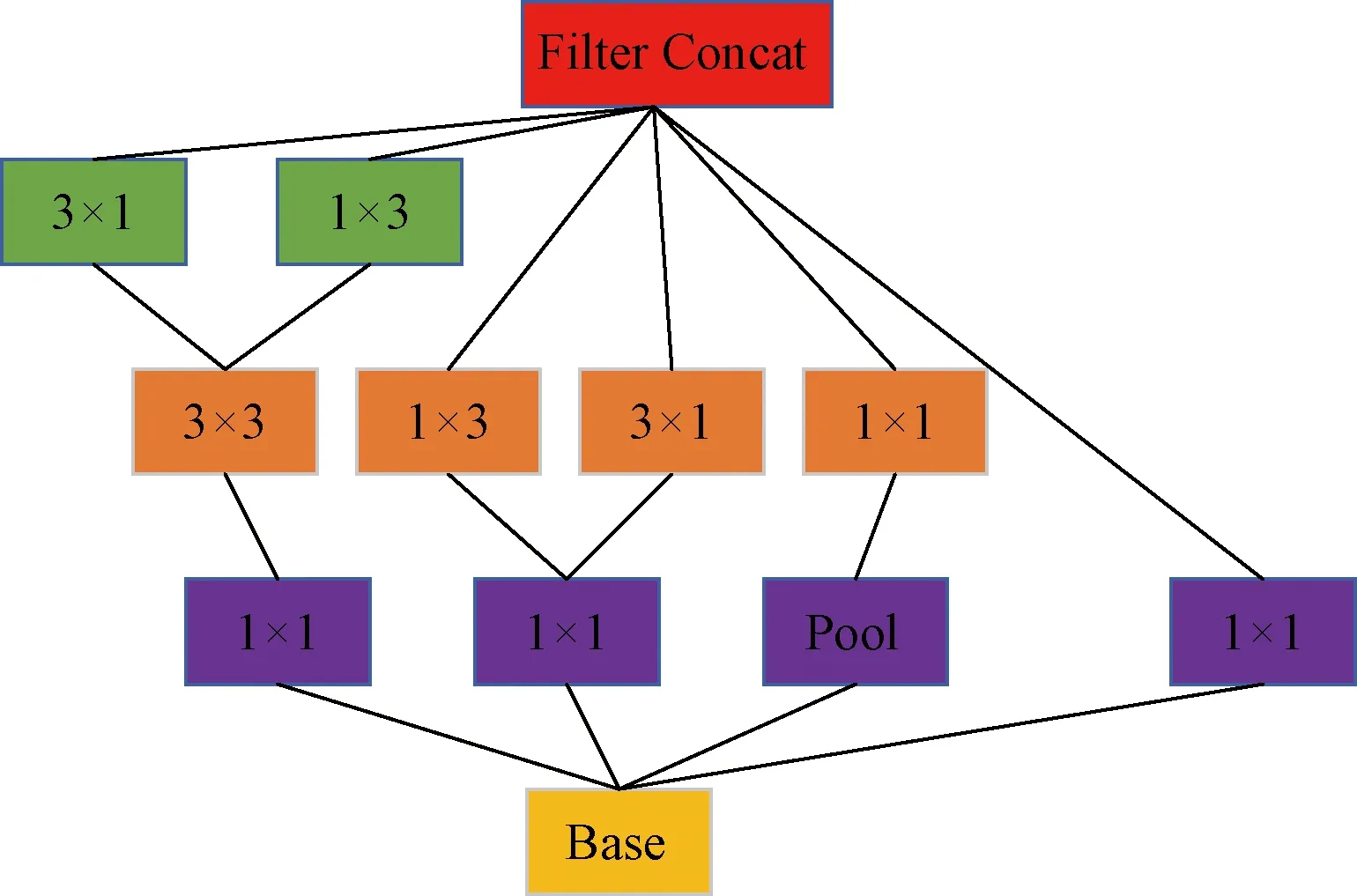
图9 模块C

为了防止出现过拟合现象，在网络中增加一个dropout层，并将其值设为0.7。将轨道数据分成72批进行处理，迭代次数为6 000次。输入的预处理轨道图像大小720×960，与25×25×265卷积核进行特征提取后进入6×6×265池化层进一步压缩特征数据，最后进入到1×1×2 048的全连接层进行参数训练，学习率设置为0.000 1。

模块A是输入被复制为4份不同的层使用，即图中3个1×1卷积层和1个最大池化层组成。第2层为2个3×3的卷积层，1个1×1的卷积层。第3层的1个卷积层为3×3。

模块B是输入被复制为4份不同的层使用，即图中3个1×1卷积层和1个池化层组成。第2层为2个1×n的卷积层，1个1×1的卷积层。第3层的2个卷积层为n×1，第4层的一个卷积层为1×n，第5层的一个卷积层为n×1。

模块C是输入被复制为4份不同的层使用，即图中3个1×1卷积层和1个池化层组成。第2层的4个卷积层为3×3、1×3、3×1、1×1。第3层的2个卷积层为3×1、1×3。

4 卷积神经网络试验结果与分析

4.1 试验样本数据

所采用的轨道图像数据集，是从安装于沿轨道行驶的测量车上的摄像机俯视拍摄轨道视频中，截取了轨道图像8 253张，其中7 123张为完好轨道图像，1 130张含有缺陷轨道；训练集中轨道图像3 521张，其中完好轨道图像3 134张，缺陷轨道图像387张；其余图像汇集在测试集中，对训练的模型进行测试。

4.1.1 权重值ω对查准率和召回率的影响

由于引入了新的损失函数，从而对网络优化方向产生了影响，需要分析ω值对网络召回率和查准率的影响。权重值ω对召回率的影响见图10，当ω≥3时召回率有大幅增加；权重值ω对查准率的影响见图11，当ω≥2的时候查准率有大幅度增加；由图10和图11可知，随着ω的增加，召回率和查准率有所升高，为了同时确保较高的召回率和查准率，确定ω≥3。

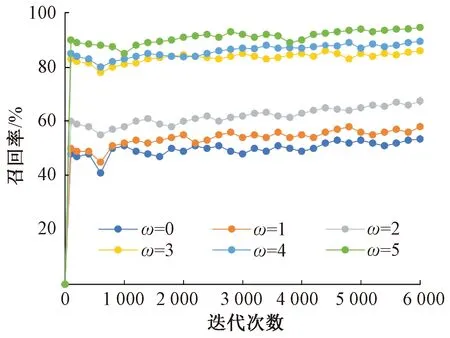
图10 权重值ω对召回率的影响

图11 权重值ω对查准率的影响

4.1.2 动态因子c对召回率和查准率的影响

为尽量避免缺陷轨道漏检的情况出现，要求有较高的召回率，所以应用不同优化器和动态因子c进行网络训练，从而获得较高的召回率和查准率。在保持ω=3不变时对c取不同值，查看Orbitcnn网络的性能表现，不同优化器和动态因子c对召回率的影响见图12，不同优化器和动态因子c对查准率的影响见图13。由图12和图13可知，当c增加时不同优化器的响应不尽相同，但在c=8 时，均方根算法RMS(Root Mean Square)召回率和查准率均达到最高，此时其召回率分别比随机梯度下降算法SGD(Stochastic Gradient Descent)和自适应梯度算法Adagrad(Adaptive Gradient Algorithm)高3%和5%，查准率分别比SGD优化器和Adgrad优化器高1.5%和3.5%。因此可以认为，c=8时的RMS为较高性能的优化器。

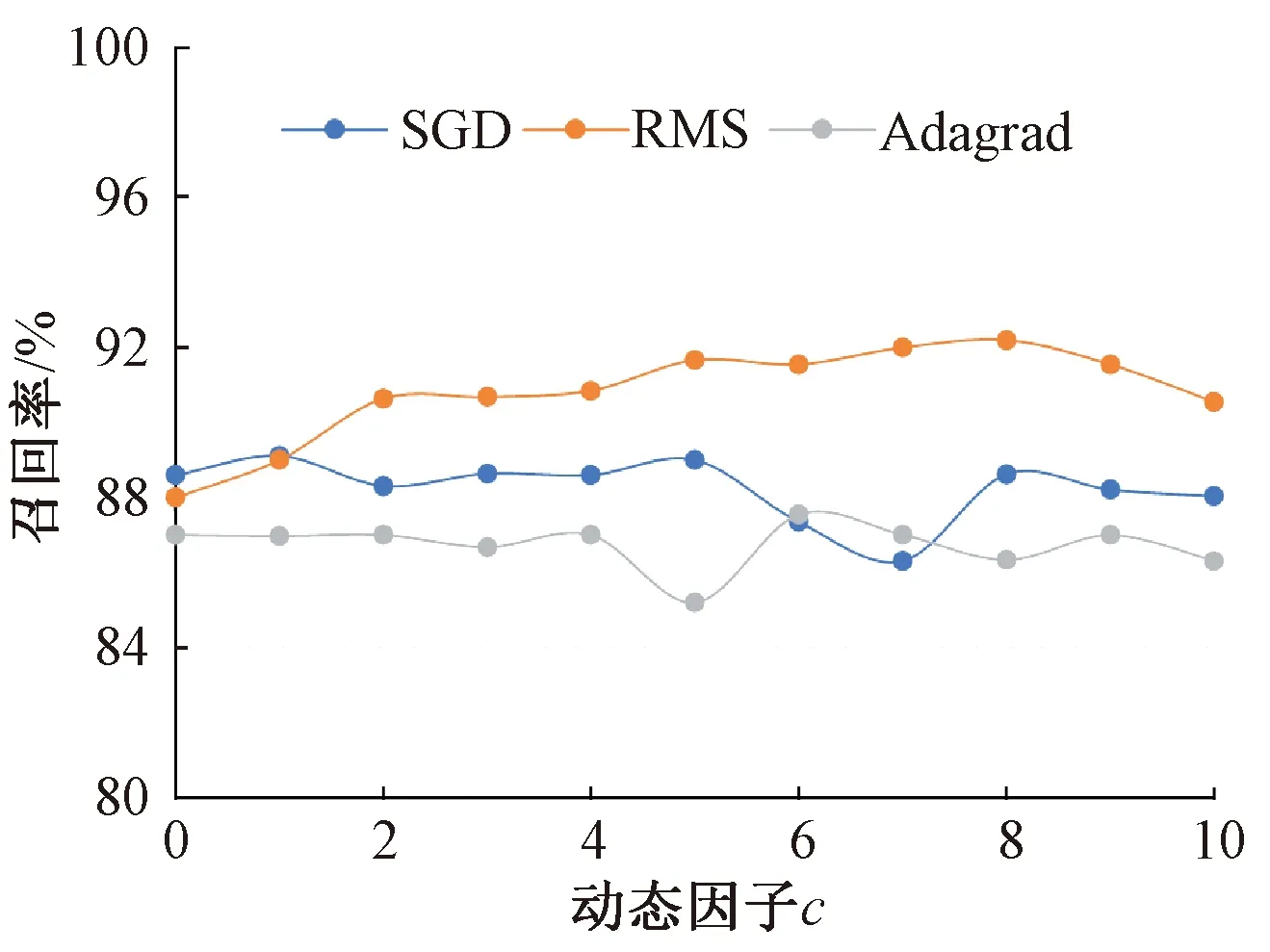
图12 不同优化器和动态因子c对召回率的影响

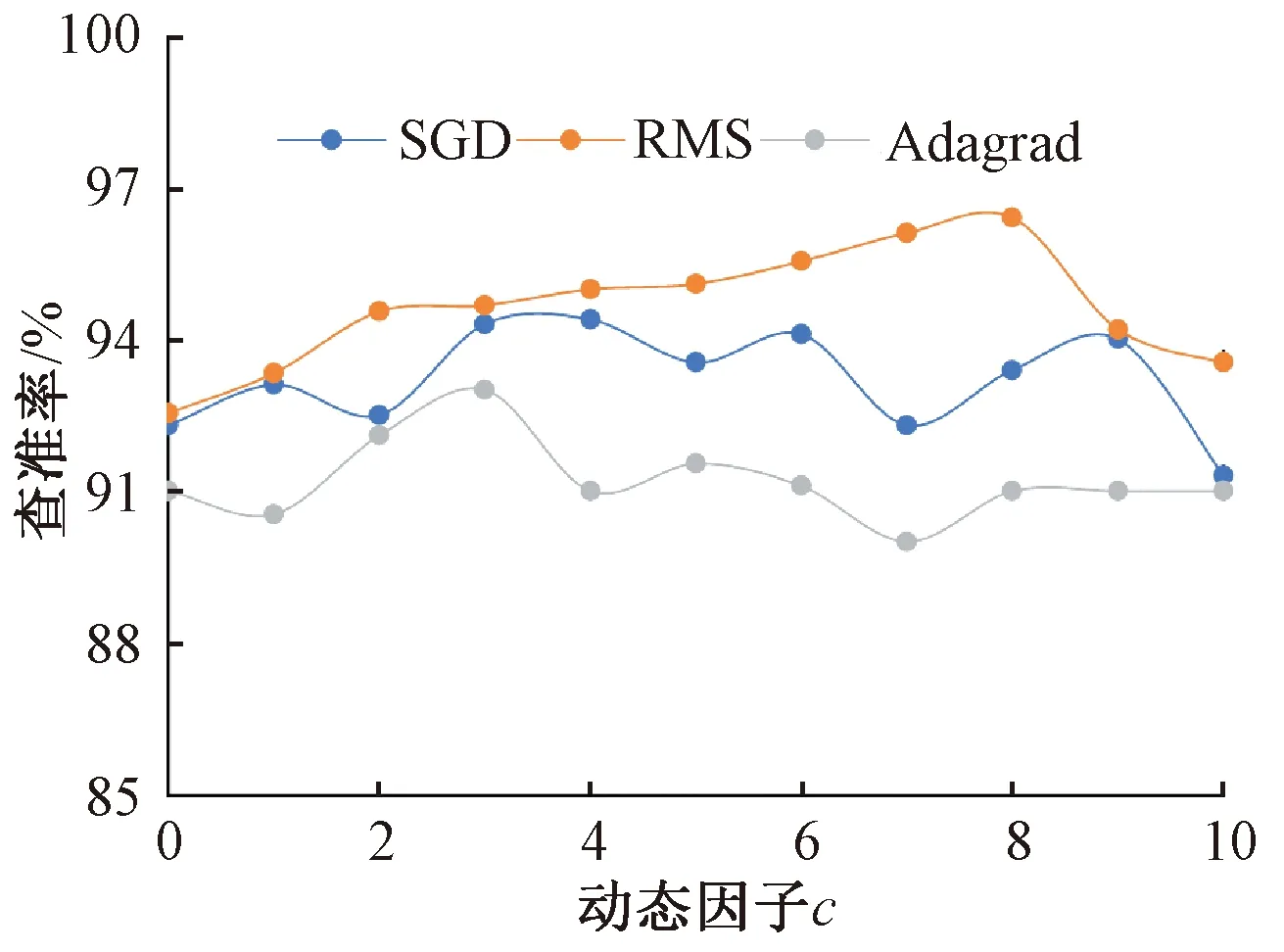
图13 不同优化器和动态因子c对查准率的影响

4.2 结果对比

将训练好的Orbitcnn与原始Inception-v3、MLC以及Cropimagecnn[18]分类器进行比较，结果如表2所示。Orbitcnn在召回率和查准率方面比MLC模型分别高了1.02%和15%，比原始inception-v3网络分别提高了2.38%和4.75%，比Cropimagecnn分别提高了1.02%和1.06%，在算法运行时间上Orbitcnn比Inception-v3节约63 ms，比Cropimagecnn节约16 ms，虽然相比MLC方法有7 ms的落后，但依然能满足实时性的要求，同时其在查准率方面相对MLC方法有大幅领先。综上可知，Orbitcnn在轨道缺陷检测上的综合性能表现优于其他模型。

表2 四种模型的比较

5 结论

(1)应用加权法对图像进行灰度化，将感兴趣区域从图像中分离，采用形态学滤波与概率霍夫变换相结合的方法进行图像形态学变换；采用阈值法去除明显不能形成连续边缘的噪声，应用离散法去除存在较多断续且离散性较大的伪边缘，得到了轨道的真正边缘；应用卷积神经网络的大卷积核分解成多个小卷积核的特性来降低特征图像的维度，提高网络的非线性以节约计算成本；构建了改进交叉熵损失函数，并对Inception-v3神经网络进行有针对性地调整，得到了轨道表面分类器Orbitcnn。

(2)采用对实拍轨道图像进行分类试验，结果表明：该方法可以在保证精度的同时，在极短的时间(平均单次识别时间为25 ms)内高效完成识别任务；在查准率、召回率和检测效率三方面综合表现优于MLC、Inception-v3和Cropimagecnn三种方法；为了最终实现轨道质量在线实时检测，尚需对轨道表面缺陷和内部结构之间的关系、分类器的在线学习以及轨道缺陷的物理定位等问题进行深入研究。