中低速磁悬浮双线简支轨道梁的冲击效应研究

王亚朋, 蔺鹏臻

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

中低速磁浮交通因其转弯半径小、爬坡能力大、运营噪声低、环境污染小且适应地形强等优点，特别适合城市中短距离的运输，在未来城市交通中具有良好的前景[1]。中低速磁浮列车通过主动调节带有控制的电磁力使列车悬浮在额定间隙附近，从而实现车辆的平稳运行，而该悬浮力的大小与悬浮间隙密切相关，因此磁浮车辆对轨道的不平顺性要求较高[2]。磁浮列车在预应力混凝土简支轨道梁上运行时，轨道梁产生的变形会改变磁浮间隙，进而改变轨道的平顺性，需要不断改变电磁力的大小来保持运行平稳性，因此该过程与轮轨交通一样，涉及车辆与轨道梁的动力相互作用问题[3-8]。相比传统轮轨交通的桥梁，磁浮轨道梁刚度小、质量轻，因此在磁浮车辆动载作用下的冲击效应对轨道梁系统的平稳性尤为重要，这也是磁浮车辆-轨道梁动力相互作用问题研究的重要内容之一。

目前国内对中低速磁浮研究中，主要侧重于磁浮车辆系统的动力学性能和悬浮控制系统[3-5]，而对于磁浮轨道梁的动力响应的相关研究较少，李小珍等[3]研究了中低速磁浮列车-桥梁系统竖向耦合振动，但并未分析F轨对轨道梁动力系数影响。耿杰等[6]以长沙中低速磁浮快线简支梁为例，实测并分析了磁浮车辆通过轨道梁时的耦合振动特性，通过实测拟合得到了动力系数关于速度的函数关系式，并未讨论与轨枕间距、扣件刚度的变化关系。刘德军等[9]构建了磁浮车辆-控制器-桥梁系统耦合动力模型，讨论和分析了典型车速、车辆荷载下桥梁、车辆和悬浮系统的动力响应，并未对冲击系数问题进行讨论分析。杨平等[10]研究了中低速磁悬浮车辆作用下车速、车重及桥梁阻尼比对20 m简支轨道梁冲击系数的影响规律，并未讨论不同轨枕间距及扣件刚度的影响。目前各国规范对动力系数的规定也不统一，在实际桥梁设计时，一般通过动力系数的经验公式，近似考虑车辆荷载的动力效应，但动力系数不仅与桥梁结构基频有关，还与行车速度、车重、扣件刚度及轨枕间距等因素有关。

中低速磁浮车辆与轨道梁的动力相互作用问题涉及桥梁动力学、车辆系统动力学、控制理论、电磁理论等多种学科，准确模拟车辆-轨道梁动力相互作用是制约该问题解决的瓶颈。本文针对我国中低速磁浮交通，建立了完整考虑滑台、迫导向等复杂运动机构的中低速磁浮车辆模型，在此基础上建立了车辆-F轨-钢轨枕-轨道梁耦合振动分析模型，对25 m双线简支轨道梁动力系数进行分析，提出了中低速磁悬浮轨道梁动力系数计算的相关建议。

1 中低速磁浮列车-F轨-钢轨枕-轨道梁耦合系统振动分析模型

将中低速磁浮车辆、U型悬浮铁、悬浮控制器、F轨、钢轨枕及轨道梁模型，按照一定的磁轨作用和空间位置关系进行组合，考虑轨道不平顺影响，建立磁浮车桥耦合动力仿真分析模型，见图1。

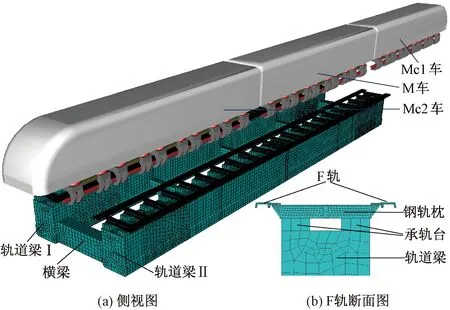
图1 中低速磁浮车-桥耦合动力分析模型

运用车辆系统动力学、电磁理论、控制理论、桥梁动力学等研究方法，分别建立车辆、F轨道、钢轨枕、轨道梁的运动方程，车辆与F轨以悬浮控制力为纽带，采用数值分析方法，求解磁浮车-桥系统动力响应[8,11]。

1.1 中低速磁浮车辆系统模型

中低速磁浮车辆主要由车体、悬浮架、悬浮电磁铁、抗侧滚梁、空气弹簧、牵引拉杆等组成。每节车体由五个悬浮架单元支撑，每个悬浮架单元由左、右两个悬浮架组成，且左、右悬浮架之间由前、后共两套抗侧滚梁连接，每个悬浮电磁铁上设置前后4个加速度传感器,车体下共5组滑台及2套迫导向机构，每套迫导向机构由T型长、短转臂及拉杆组成。每节车辆模型中，车体和悬浮架分别考虑伸缩、横移、沉浮、侧滚、点头、摇头共6个自由度，U型悬浮铁考虑伸缩、沉浮、点头共3个自由度，抗侧滚梁仅考虑摇头自由度，T型长、短转臂仅考虑摇头自由度，第1、3、5组滑台考虑横移自由度，第2、4组滑台与车体固结。空气弹簧、牵引拉杆等视为弹簧-阻尼单元。每节车辆模型共计216个自由度，见表1，三编组车辆共计648个自由度。

表1 车辆模型自由度

根据达朗贝尔原理可建立车辆系统动力方程[11]

(1)

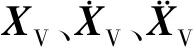
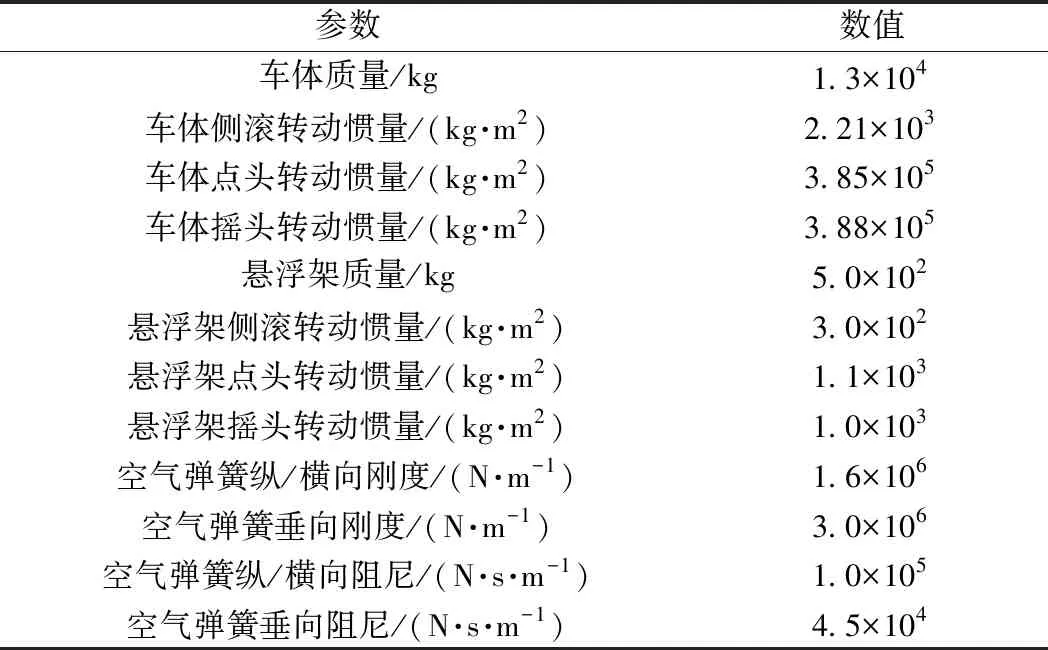
表2 中低速磁浮车辆主要计算参数(24 t车重为例)

1.2 F轨、钢轨枕、轨道梁系统模型

F轨、钢轨枕、轨道梁均采用有限元法建立，因此根据达朗贝尔原理分别建立F轨、钢轨枕、轨道梁的运动方程

(2)

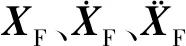
1.3 U型磁铁悬浮控制系统模型及电磁力计算

中低速磁浮列车依靠吸力悬浮，系统自身不能自稳，必须加入主动控制，通过计算电磁铁的位移、速度和加速度，将该结果输入给控制系统，计算得到电磁力大小，并反馈给多体系统，如此反复迭代，使得列车在额定间隙附近稳定悬浮[10-11]。

对于图2所示中低速磁极模型，由于角点的存在只对磁场的局部区域产生影响，并导致产生横向力，即当产生横向距离y时产生横向力Fy，使得U型磁铁恢复到轨道中心线位置，垂向力大小按照电磁铁宽度Wm增加一个附加宽度δ时按照平行区域磁场强度分布计算得到。图2中U型磁铁单侧矩形磁极为细长型矩形磁铁，可将其简化为单位长度的图3所示二维模型问题。S为悬浮间隙；N为线圈匝数；Wm为极板宽度。

图2 具有横向位移y的U型磁铁与F轨道模型

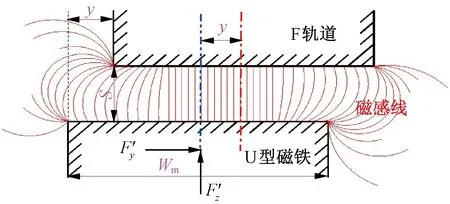
图3 矩形磁极二维四角问题模型

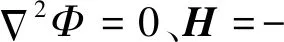
dF=μ0[H(H-dS1)-0.5H2dS1]

(3)

式中：μ0为真空磁导率；dS1为间隙S中包围产生电磁力的一个闭合曲面在投影平面的闭合曲线的线积分。

参考文献[12-13]，图3所示四角问题经保角变化及根据柯西-黎曼方程，再根据式(3)计算得到图3所示模型在单位长度电磁铁发生横向位移y时的垂向力与横向力

(4)

对于图2所示完整U型磁铁，根据式(4)，对于长度为l0的U型电磁铁垂向力与横向力

(5)

对于图2所示电路，假定铁芯磁通等于气隙磁通，全部磁阻等于气隙磁阻，则此时整个回路中的电流则为I=0.5I′，带入式(5)化简

(6)

式中：F=μ0AN2I2/(4S2)，A=l0Wm。

由式(6)可知，F=μ0AN2I2/(4S2)恰好为图2所示磁路中假定气隙均匀分布，并忽略磁阻和磁通饱和得到的电磁力计算式，即Brezina基于平面矩形磁极的二维电磁力计算式。因此可先计算F，再计算U型磁铁所需要的垂向力与横向力。令λ=2S0/(πWm)，S0为额定气隙，则式(6)可进一步化简

(7)

根据电磁定律计算电压方程

(8)

式中：R为磁阻，R=2S/(μ0A)；Ψ为线圈的磁链；L为绕组瞬时电感，L=μ0AN2/(2S)。

引入电压控制模型

(9)

式中：U0为额定电压；I0为额定电流；F0为额定电磁力；Us为位移反馈系数；Uv为速度反馈系数；Ua为加速度反馈系数；Uis为在不同荷载条件下维持恒定的额定间隙引入的积分项反馈系数。

将式(7)带入式(8)，得到最终的控制模型

(10)

结合式(7)与式(10)编写中低速磁浮U型磁铁控制模型见图4。

图4 基于电压的中低速磁浮控制流程

1.4 电磁力与F轨的传力计算

电磁力F作用于F轨单元(本文采用6面体8节点单元)时，首先判断其作用单元位置(设此刻单元为单元m)，再判断力作用到单元的具体位置(设该位置为n)，通过坐标变化，建立该单元自然坐标系(ξ,η,ζ)下的八结点六面体等参单元(即为母单元)，单元形函数取

i=1,2,…,8

(11)

位移u的插值函数取

u=α1+α2ξ+α3η+α4ζ+α5ξη+α6ηζ+

α7ζξ+α8ξηζ

(12)

式中：α1～α8为待定系数，由结点上的函数值ui确定。单元其他两个方向位移v和w的插值函数取与式(12)相同形式。可知式(12)中一个自变量固定时，函数为另外两个自变量的双线性函数，因此在立方体单元每个侧面上，该插值函数由该面四个结点的函数值唯一确定，故相邻单元公共面上，只要在其中四个公共结点上函数值相同，插值函数就一定是连续的。式(12)可写为

(13)

式中：Ni(ξ,η,ζ)为多项式函数，在结点i处取值1，其余结点取0。

因此单元m的n点作用电磁力Fn时，各结点力的分配可按下式进行计算

(14)

式中：Fex=[Fx1,…,Fx8]T；Fey=[Fy1,…,Fy8]T;

Fez=[Fz1,…,Fz8]T；ξn,ηn,ζn为点n的无量纲坐标，即为单元自然坐标系下；Fnx、Fny、Fnz为力Fn的投影。

由以上分析，可将电磁力作用到轨道梁上，实现磁浮列车与轨道梁的动力相互作用。

2 算例背景

针对某中低速磁浮快线上一孔25 m双线简支梁桥进行车桥耦合振动分析，该线路设计为双线，设计速度最高100 km/h。单线轨道梁梁宽1.4 m，梁高2.1 m，梁体采用C50混凝土；两幅轨道梁之间设置5道横梁连接为整体，端部横梁顺桥向宽0.6 m，高1.2 m，中横梁顺桥向宽0.3 m，高0.8 m。承轨台高0.208 m，宽0.4 m，纵桥向宽0.6 m，采用C40混凝土。F轨与钢轨枕固结，钢轨枕通过扣件与承轨台连接，扣件下垫橡胶垫片。每片轨排长12.5 m，纵桥向相邻轨排间通过指型板连接成整体。图5分别给出了简支梁跨中截面和F轨、钢轨枕、承轨台截面尺寸。

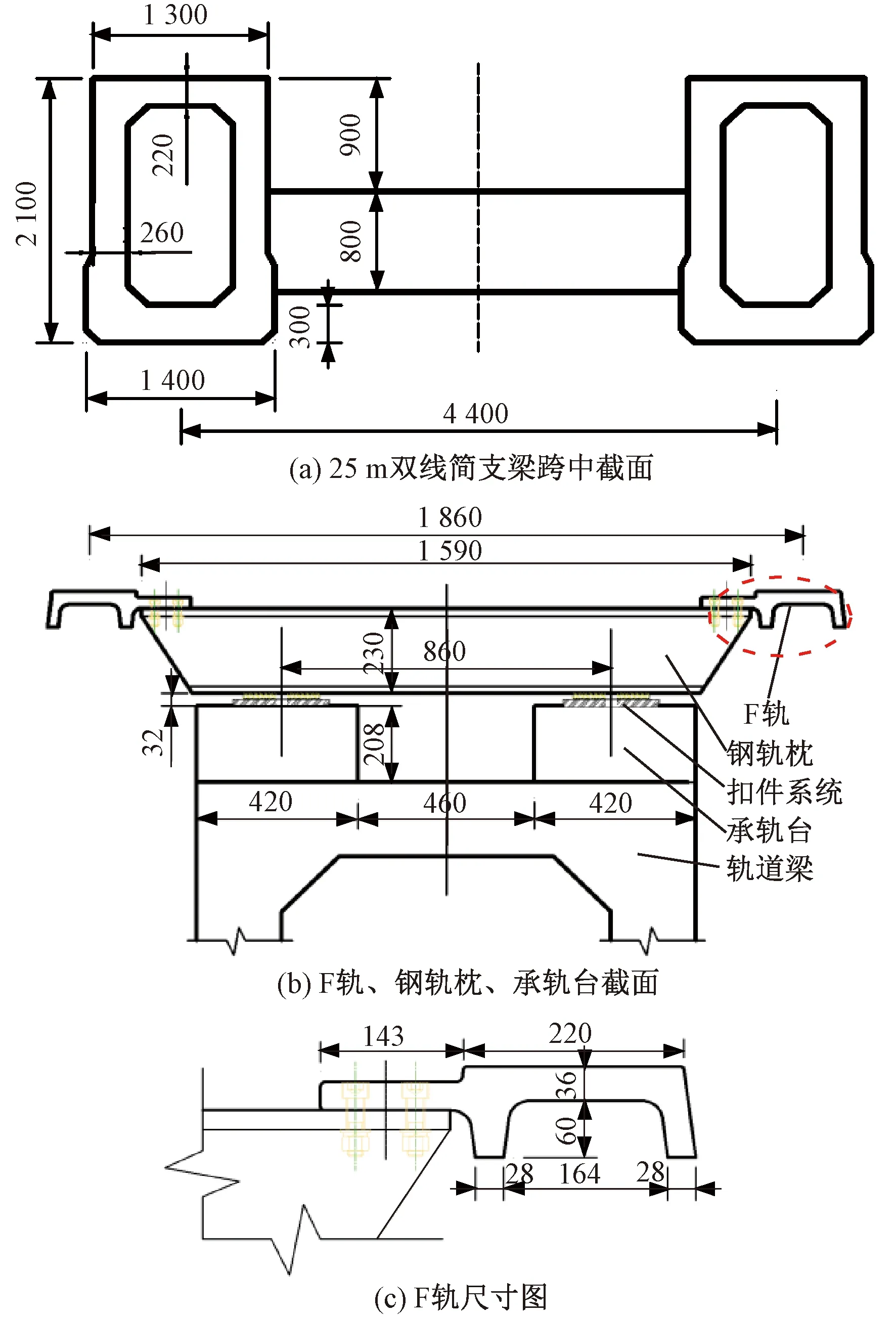
图5 结构尺寸图(单位:mm)

F轨、钢轨枕、轨道梁采用Ansys软件建立三维实体模型。扣件、指型板采用线性弹簧-阻尼力元考虑。F轨与钢轨枕通过螺栓固结。轨道梁按照实际简支受力施工模型约束。

中低速磁浮车辆多刚体模型采用UM软件建立，编组形式为“Mc1+M+Mc2”。电磁力控制模型采用公式(9)的电压控制模型。

本文采用文献[3,10]中提供的针对磁浮柔性高架线路随机不平顺谱理论推导得到的不平顺功率谱，其函数为：φ(ω)=Ar/ωn，其中ω为空间波数(本文取为3 000)，n为频率特征参数(本文取为2)，Ar为表面粗糙度系数(取6.1×10-8)。依次生成10组随机不平顺样本共分析，其中某条左垂向不平顺见图6。

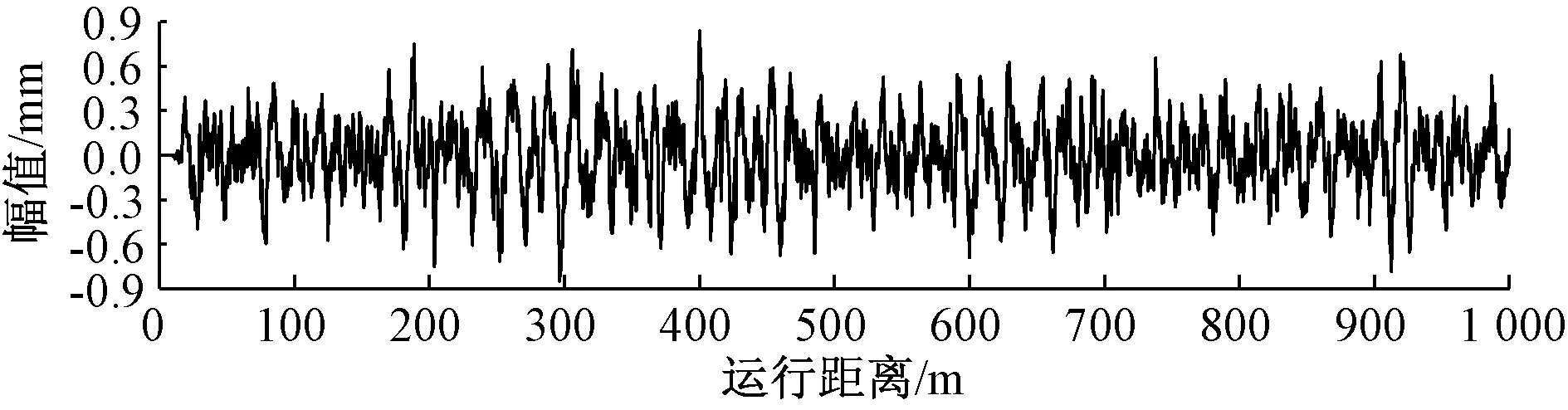
图6 左轨道垂向不平顺

磁浮车-桥耦合系统动力学微分方程组为刚性微分-代数方程组，因此本文采用Park[14]提出的刚性稳定法进行该方程组的积分求解，该方法为“预估-校正”格式的隐式变步长迭代算法[15]。

仿真工况见表3，分析各参数对轨道梁动力冲击系数的影响，取10条不平顺计算值的平均值作为最终值。磁浮混凝土轨道梁相关规范规定见表4。

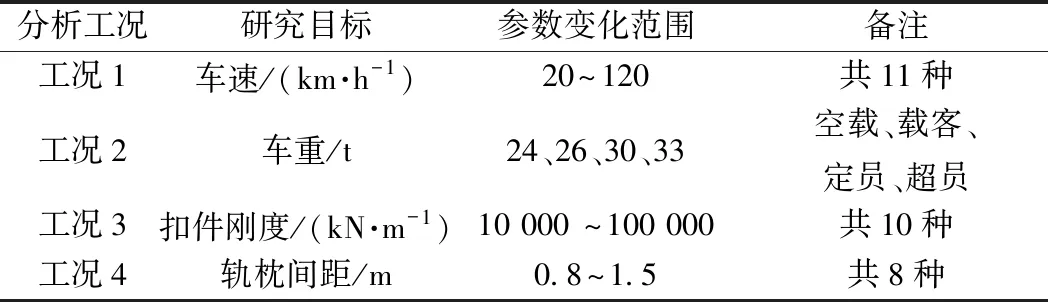
表3 分析工况

表4 磁浮混凝土轨道梁(直线)动力系数φ规范规定

为验证模型正确性，取轨枕间距1.0 m、车重24 t (空载)、车速90 km/h仿真结果，与文献[6]提供实测结果进行对比，见图7。由图7可知,该仿真结果与实测结果基本吻合，因此该模型可作为前述车桥耦合动力分析计算。

图7 轨道梁仿真与实测结果对比

3 轨道梁动力系数分析

3.1 车速变化对轨道梁动力系数的影响

为分析中低速磁浮车辆通过轨道梁时，车速变化对轨道梁动力系数的影响，选取表3分析工况1，统计不同轨枕间距、车速下轨道梁Ⅰ的动力系数见图8。由图8可知，中低速磁浮车辆以20～120 km/h通过25 m双线简支轨道梁时：①不同轨枕间距下轨道梁动力系数随车速增大而增大，这一规律与普通铁路桥梁的动力系数趋势一致，但相同速度不同轨枕间距时冲击系数并非随间距增大而增大或减小，尤其是当速度较低时此规律更不明显，整体而言刚度较低时冲击系数增长较为缓慢；②该分析工况下，轨道梁动力冲击系数变化范围为1.011～1.131，对比120 km/h速度下轨道梁时域曲线可知轨枕间距较大时存在共振现象，而较小时共振不明显；③与国内外相关规范对比，该结果且大于文献[17]和文献[20]规定，而小于其他4种规范的设计取值。

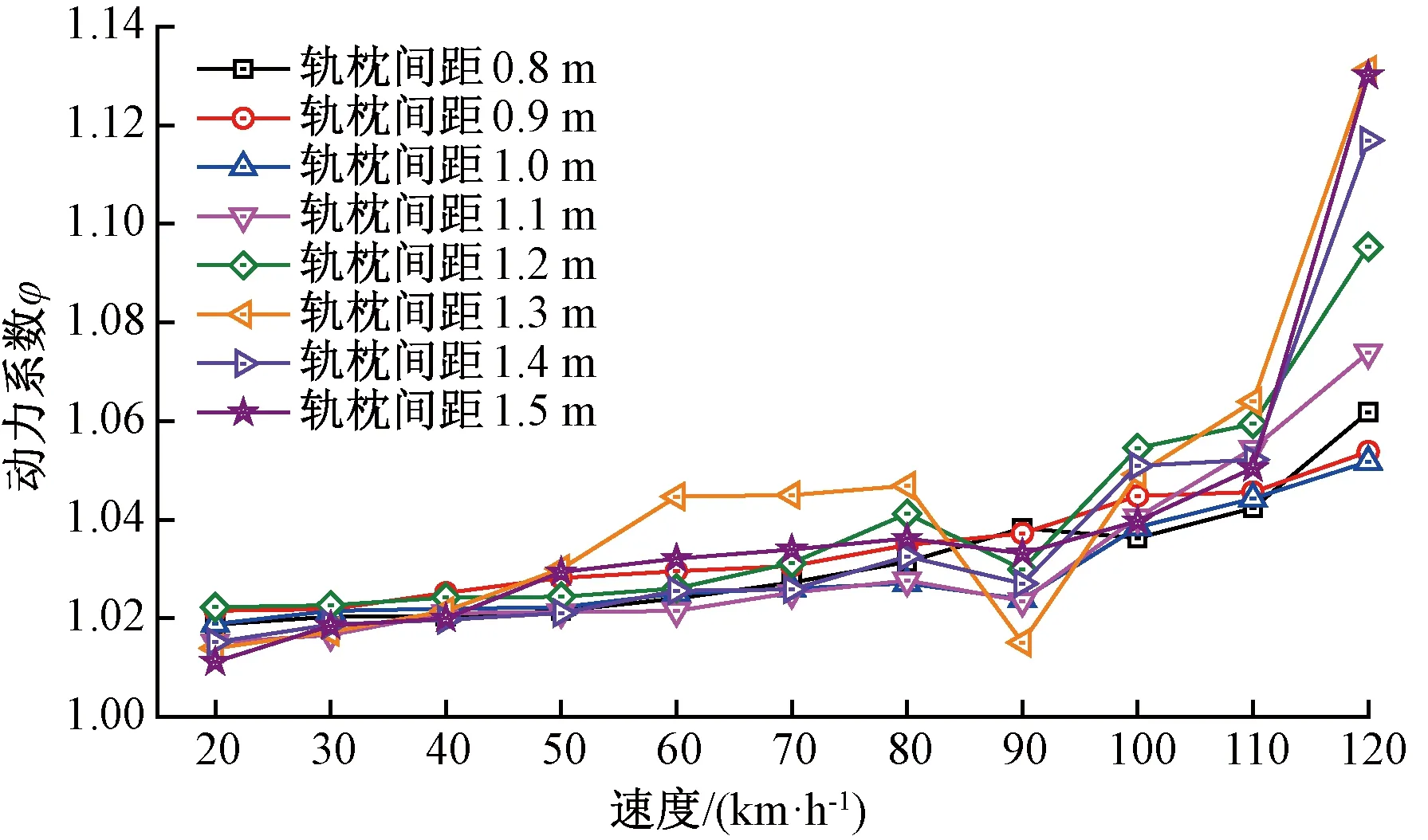
图8 速度变化对轨道梁动力系数的影响

3.2 车辆质量变化对轨道梁动力系数的影响

为研究车辆质量变化对动力冲击系数的影响，取车辆空载、座客、定员、超员载荷四种情况，对应车辆重量为24、26、30、33 t，其他各参数保持不变。不同轨枕间距、车辆质量下，轨道梁Ⅰ动力系数见图9。由图9可知：①整体而言轨道梁跨中动力系数随车辆质量增大而增大，但结果不同质量下动力系数相差较小，部分轨枕间距下随质量增大先增大后减小，这是由于该工况下系统共振所引起；②该分析工况下，轨道梁动力系数变化范围为1.014～1.038，与国内外磁浮规范相比，该动力系数介于文献[17]规定的1.1和文献[20]规定的1.0之间，小于其他5种规范的设计取值。

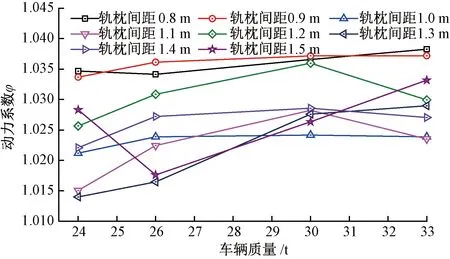
图9 车辆重量变化对轨道梁动力系数的影响

3.3 枕下扣件刚度变化对轨道梁动力系数的影响

中低速磁浮钢轨枕通过扣件系统与轨道梁的承轨台连接，扣件系统由轨枕下胶垫及连接螺栓等组成。为研究枕下扣件刚度变化对轨道梁动力系数的影响，取表3所示分析工况3，统计不同轨枕间距、扣件刚度下轨道梁Ⅰ动力系数见图10。由图10可知：①整体而言轨道梁动力系数随扣件刚度增大而增大，个别轨枕间距下会先增大后减小，这是由于该轨枕间距及扣件刚度共同影响下轨道梁与车辆频率接近，存在共振现象所导致；②该分析工况下，轨道梁动力系数变化范围为1.010～1.077，与国内外磁浮规范对动力系数规定相比，该结果大于文献[20]规定的1.0，而小于其他5种规范的设计取值。

图10 轨下扣件刚度变化对轨道梁动力冲击系数的影响

中低速磁浮车辆通过不同扣件刚度、轨枕间距时轨道梁Ⅰ的跨中挠度见图11。由图11可知，随着扣件刚度的增大，轨道跨中挠度减小，且呈反比例函数形式减小，这是因为F轨、钢轨枕与轨道梁组合成为一个空间体系，其整体竖向抗弯刚度随扣件刚度增大而增大，在相同车辆荷载作用下，轨道梁挠度将减小，因此减小轨枕间距，可有效降低轨道梁跨中挠度。

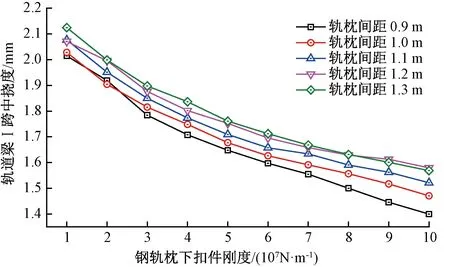
图11 轨下扣件刚度变化对轨道梁跨中挠度的影响

3.4 轨枕间距变化对轨道梁动力系数的影响

为研究轨枕间距对轨道梁动力冲击系数影响，取表3所示分析工况4，不同速度、车辆质量、扣件刚度随轨枕间距变化见图12。由图12可知：①相比轮轨关系的车桥耦合动力问题，磁轨关系的车桥耦合问题其动力冲击问题规律性并不明显，整体而言轨道梁动力系数随轨枕间距会减小，当轨枕间距为1.2 m时，较大的扣件刚度使得系统共振更明显；②相比车辆质量变化，速度、扣件刚度变化对轨道梁动力系数影响显著；③该分析工况下，轨道梁动力系数变化范围为1.010～1.131，与国内外磁浮规范对动力系数规定相比，该结果大于文献[17]和文献[20]规定，而小于其他4种规范的设计取值。

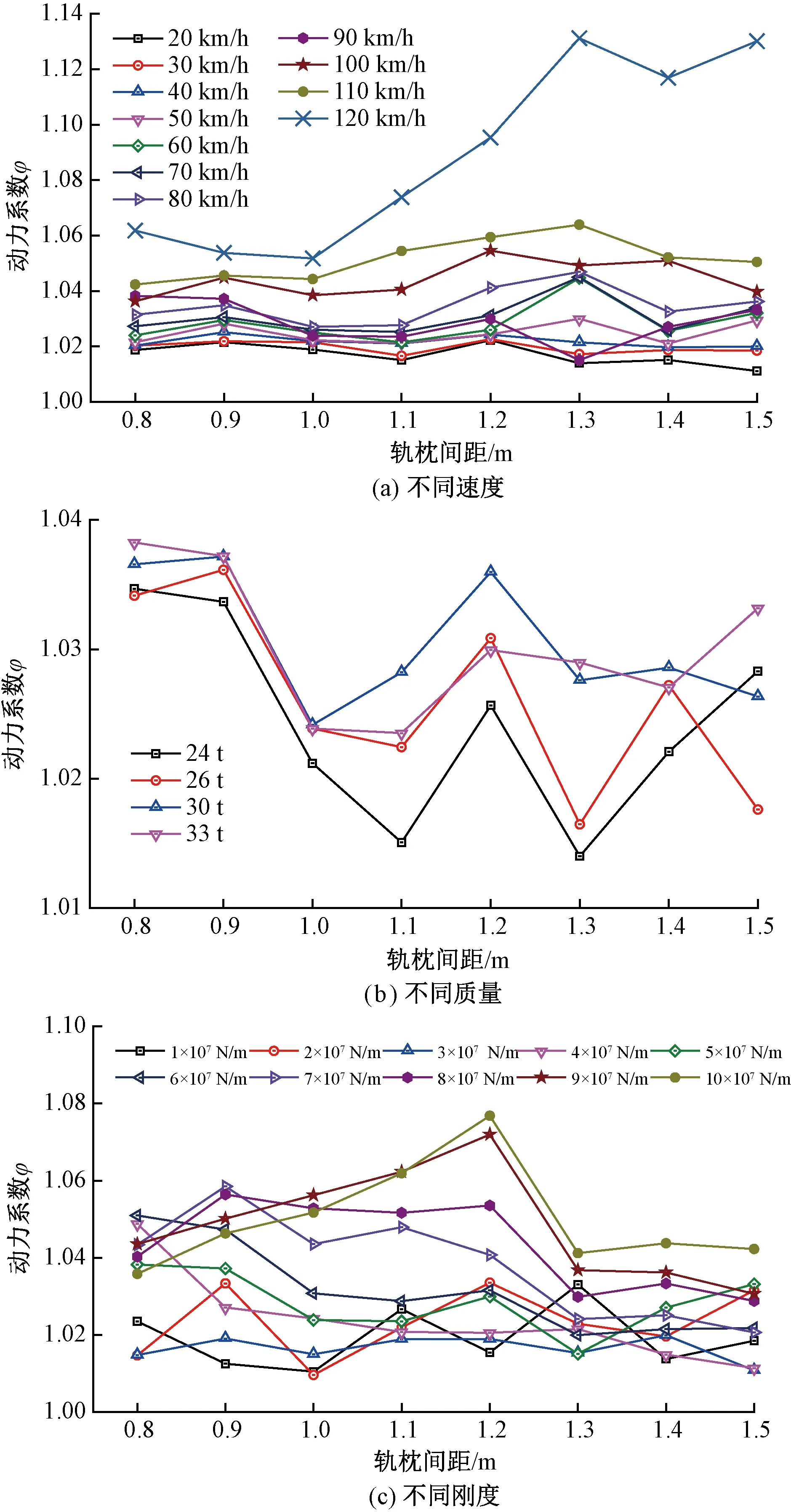
图12 轨枕间距变化对轨道梁动力冲击系数的影响

4 结论

本文以某中低速磁浮快线25 m双线简支轨道梁为研究对象，基于UM和Ansys联合仿真，建立了中低速磁浮车辆-F轨-钢轨枕-轨道梁动力相互作用模型，通过与该线实测结果对比验证了模型正确性，重点研究了车速、车重、扣件刚度及轨枕间距对轨道梁动力系数的影响，主要结论如下：

(1)本文基于电磁铁理论和PID主动悬浮控制原理建立了适用于中低速磁悬浮车辆-轨道梁动力相互作用的分析模型，通过与实测结果的对比具有较好的精度，说明本文模型可用于分析中低速磁浮轨道梁的动力冲击效应。

(2)由于磁浮车桥耦合系统的复杂性，共振极易出现，规律性不太明显，整体而言轨道梁动力冲击系数随车速、车辆质量、轨下扣件刚度增大而增大，随轨枕间距增大而减小。

(3)算例结果分析表明，各分析工况下，中低速磁浮轨道梁动力系数最大为1.131，其值大于文献[17]和文献[20]的取值，接近文献[19]规定的1.15，而对所有计算的动力系数值统计可知，约99%的计算值小于等于1.10，而95%的数据点小于等于1.06，这表明文献[20]对动力系数的取值偏小，不利于桥梁的运行安全，而文献[19]规定的1.15偏大，文献[20]的1.10取值较为合理。

(4)磁浮车辆与轨道梁的动力相互作用是个复杂的系统问题，由于PID主动悬浮控制存在，轨道不平顺的随机性对系统影响很大，极易出现共振现象，本论文将电磁力简化为集中力进行分析，与均布荷载时结果以及不同电磁力计算公式情况下的结果进行对比，下一步将结合电磁有限元分析手段，使得计算模型更接近实际工作状态，对F轨及轨道梁动力问题细致分析。