柔版印刷油墨转移特性研究
刘美华,李 艳*,袁英才,乔俊伟,金 琳
(1.数字化印刷装备北京市重点实验室,北京 102600;2.印刷装备北京市高等学校工程研究中心,北京 102600;3.北京市印刷电子工程技术研究中心,北京 102600;4.上海出版印刷高等专科学校,上海 200093)
近年来,随着社会发展的需要,柔性版印刷技术以其绿色环保的优势在全球范围内得到快速发展[1],其应用领域也在逐渐拓展.柔版印刷是一种利用雕刻了着墨孔的网纹辊施墨、以可挠曲材料作为印版的轮转凸版印刷方式[2].在柔印过程中,网纹辊的施墨过程是均匀准确地控制油墨转移量的关键环节[3].
随着数字化技术和新材料的发展,柔版印刷电子在高新技术产业得到了广泛的应用[4],如太阳能电池、触摸屏、RFID(无线射频识别)标签、OLED(有机发光元件)等.因此,研究网纹辊的油墨转移情况对柔印技术的发展有重要意义.本文通过将网纹辊运动简化为槽与版之间一个网穴单元的运动,使用守恒定律建立了油墨转移过程的数学模型,并通过仿真验证了这一模型的可行性.
1 油墨接触印版滚筒的临界状态分析
网穴中的油墨受表面张力的控制,在一段时间内保持固定状态.以恒速接近印版的过程中,在某一临界时刻,油墨液体分子会与印版表面气体分子接触,两者之间形成分子力,出现润湿现象,见图1.
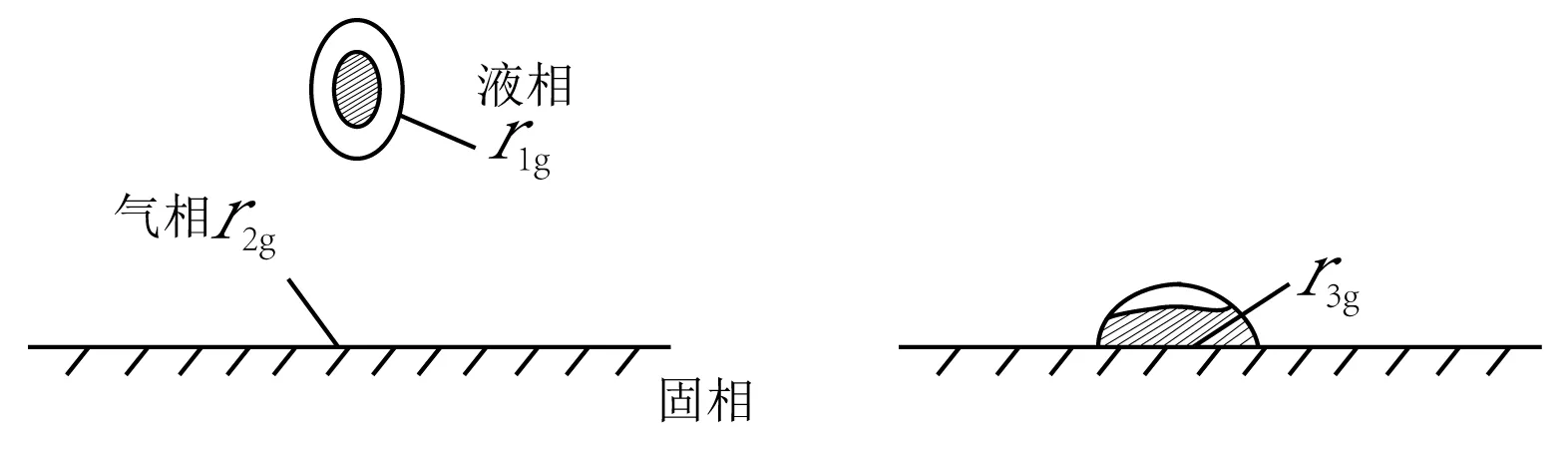
图1 润湿现象示意图
由热力学第二定律可知,在温度、压强不变的条件下,体系的能量ΔG≤0时,润湿过程才可以自发地进行,即固-液界面增加的自由能r3g、液体和固体表面减少的自由能r1g、r2g需要满足以下公式:
△G=r3g-r1g-r2g≤0,
(1)
或者体系对外所做的黏附功为
Wa=r2g+r1g-r3g≥0.
(2)
体系对外所做的黏附功是逐渐增大的,所以从能量角度有利于油墨径向扩散.以此刻为起点,油墨会在间隙中扩散,印版表面的大气分子逐渐被液体分子替换.根据Asakura和Oosawa“构型熵”改变来源于高分子链和表面相互作用的理论[5],根据平板硬球模型[6],可得到在转移临界状态时,油墨受力主要来源于排空力,排空力的表达式如下:
(3)

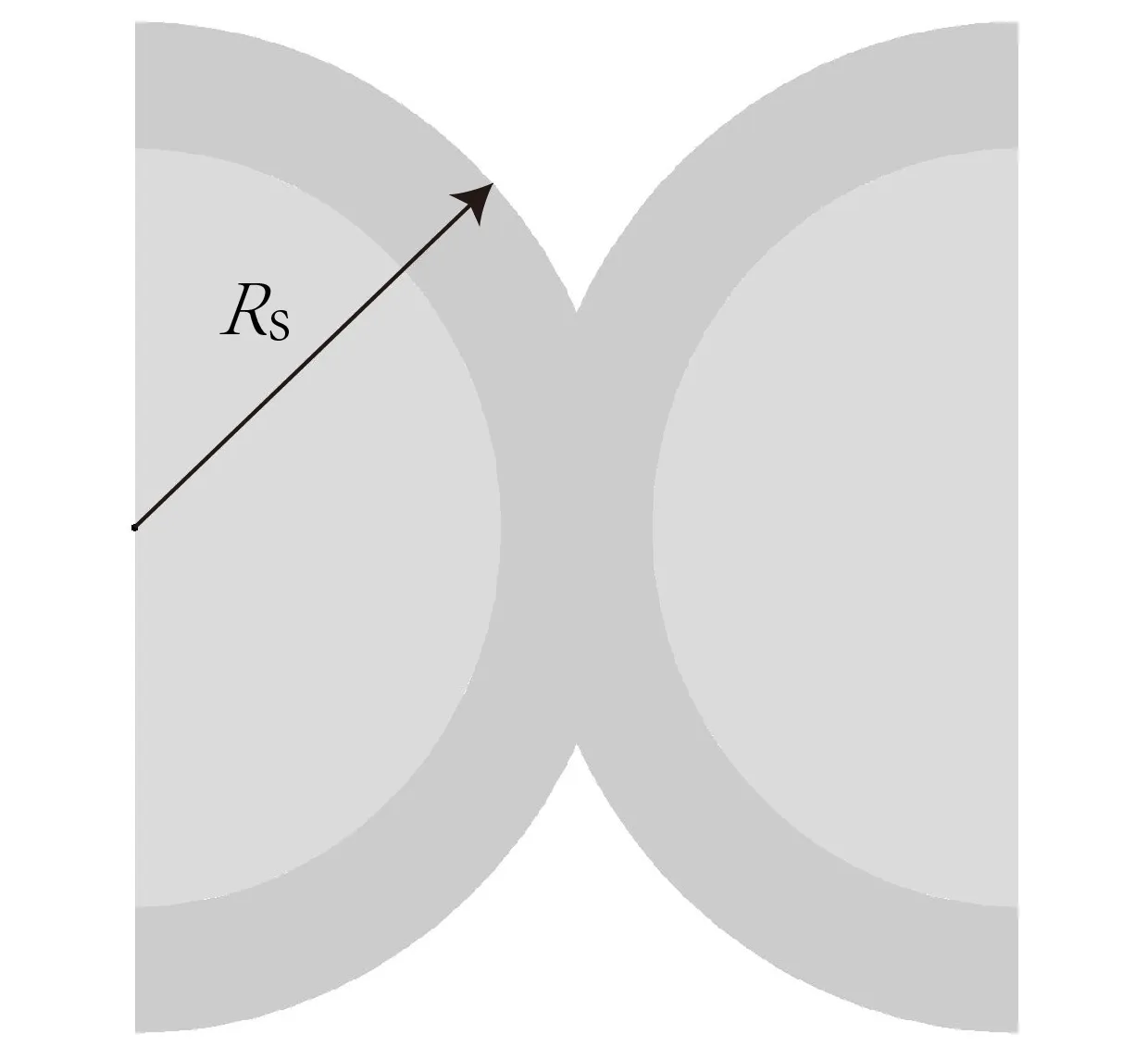
图2 排空力来源:溶液颗粒交叠体积
2 间隙处黏滞状态模型分析
为了便于探究规律,创建一个适用于有弹性版的印刷间隙内存在黏性油墨流动的数学模型,根据网穴与印版接触区结构、油墨层内动态压力作用,预测油墨在转移过程中的液体桥拉伸流变情况.
当网穴内部的油墨与网穴与印版之间的油墨逐渐形成压差,克服网穴材料渗透性所带来的流动阻力,驱动流体流出网穴.当压差不足以克服阻力时,液体桥的剪切运动在将液体从凹槽中拉出的同时,表面张力会将其滞留在网穴腔边缘,增加固液接触面积,提高黏性强度,限制转移率.
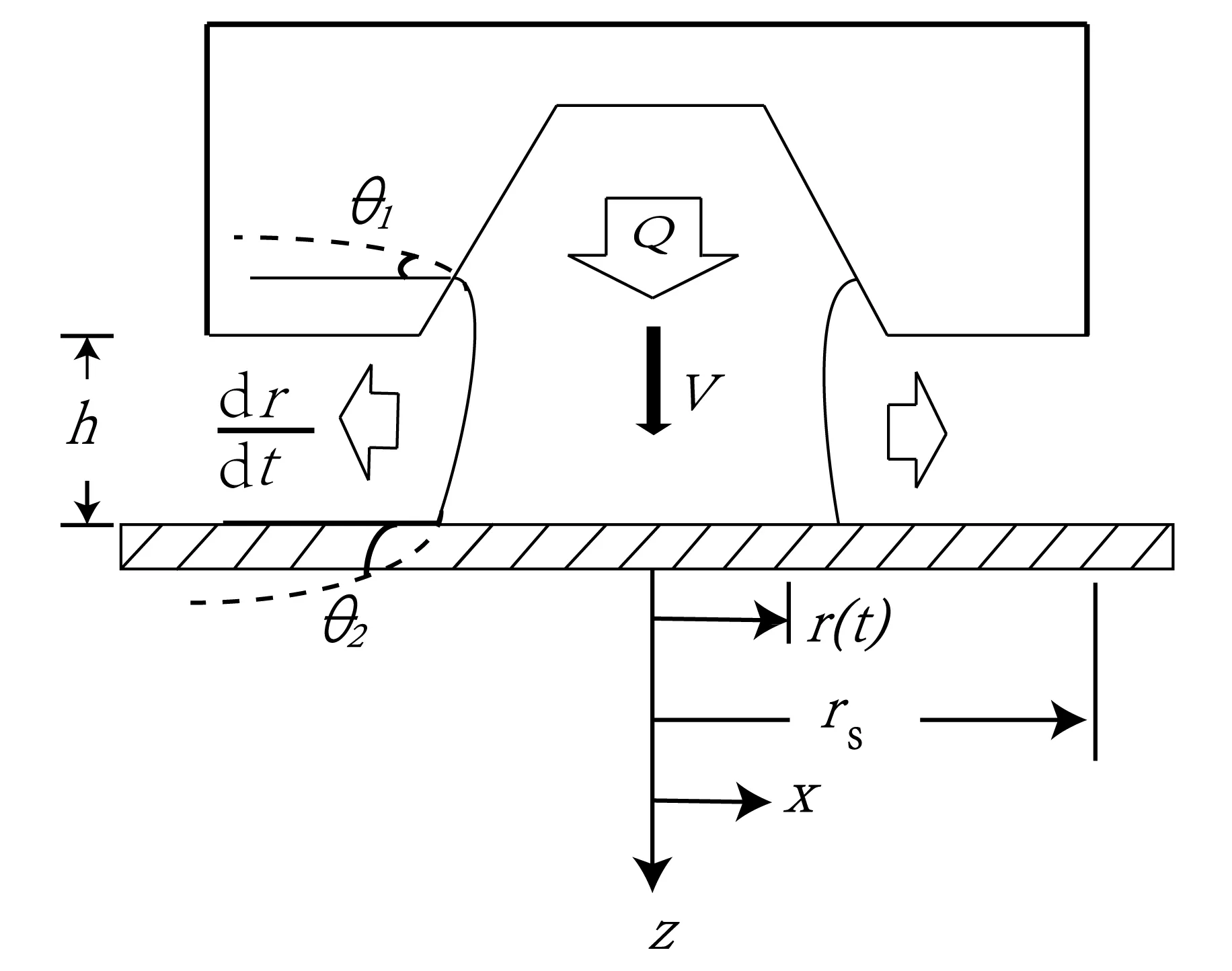
图3 间隙中油墨转移示意
根据图3所示模型可以得到油墨转移体积流量Q[7],
(4)
式(4)中,kzz为轴向渗透率,krr为径向渗透率[8],ΔP为液滴表面到其内部的压力差,r为印版上油墨铺散半径,μ为油墨黏度.
体积守恒定律:
(5)
式(5)中,t为油墨接触印版瞬间的计时时间,ρ为油墨的密度,r为印版上油墨铺散半径,h为给定时间内网纹辊与印版的高度间隙.将式(4)带入式(5)得
(6)
由于网纹辊以恒定的速度va运动,导致了润湿半径r持续变化,并改变了网纹辊传递油墨的体积流率.
(7)
利用式(7)将式(6)的左半部分展开得
(8)
h=ha-vat,
(9)
其中,ha是油墨开始接触印版滚筒那一时刻网穴的高度.
定义临界速度为v*,此刻油墨扩散半径r=rs,则
(10)
式(8)可转化为
(11)
将式(9)带入式(11)得
(12)
两边取积分得
(13)
常数c可以从初始条件t=0,r=0开始,整理可得
(14)
即
(15)
定义油墨扩散平均速度为vs,则
(16)
将v*无量纲量化处理可得
(17)
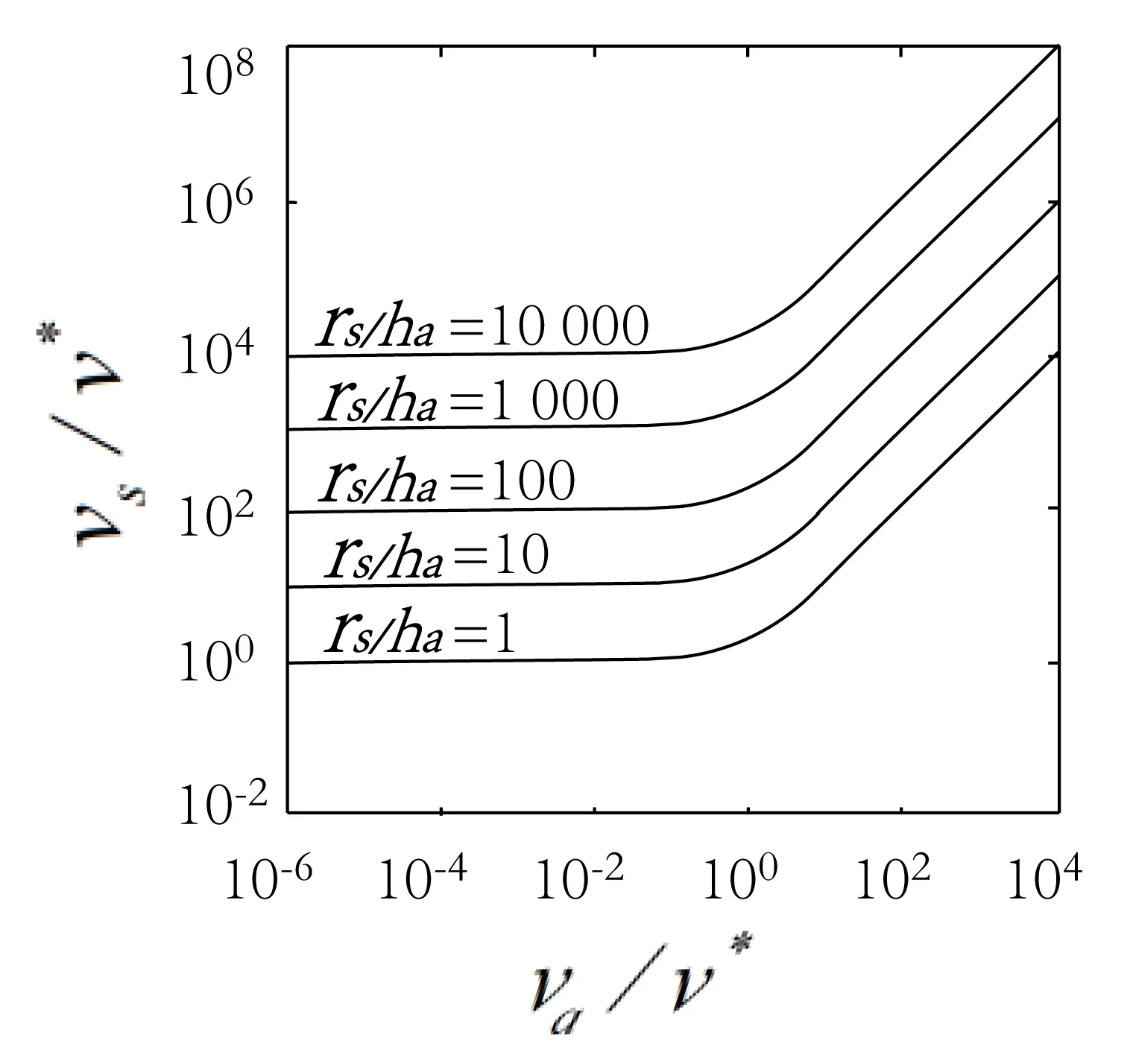
图4 接触速度与油墨扩散速度之间函数关系
将式(17)函数绘图可得图4,由图4可知在不同网纹辊接触速度下,油墨扩散速度呈现两种不同的状态.在速度较小时,毛细力是驱动液体流动的主要动力,流动速度受到黏性力的控制,黏性力阻止油墨流出网穴,油墨扩散速度为常数,即:
(18)
(19)
式(19)中γ为表面张力系数,l为液体弯月面曲率半径,θ1、θ2为油墨上下接触角,由式(19)可知伴随着速度增大毛细力逐渐增大;当速度较大时,油墨扩散速度与网纹辊接触速度成正比,即
(20)
在高速极限状态下,毛细现象对油墨的转移没有很大影响[9],接触印版的油墨经过间隙变形产生挤压流动.在此模型中,忽略油墨在间隙中由于流动引起的黏性压降,假设黏性压降与将油墨挤压出网穴的压力相比可以忽略不计.根据黏性流动学关于二者压力差公式:
(21)
其中,v是径向运动过程中的速度差距,z为平板间距,x为液体扩散半径.
通过分析可以得到,在高速状态下传墨,压差的产生并不足以驱动油墨扩散,间隙变形驱动了油墨的转移运动;然而在低速状态下压差的产生会对运动状态产生重要影响,在不同速度下,根据LLD液膜理论[10],网穴与印版分离后残留膜厚e存在重要的标度关系:
e~k-1(Ca)2/3,
(22)
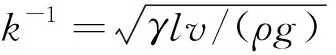
3 油墨自由表面变化

表1 仿真模型参数
XFlow作为新一代广泛应用于研究自由表面及多相流问题的 CFD 软件[11],具有易于使用、边界条件处理方便、不需要对流体区域划分网格、表面复杂性低的优点[12].同时,基于波尔兹曼方程的最小动力学模型而发展出来的离散格式,能够可靠地替代常规的CFD技术[13].在使用数值模拟软件进行模拟实验时必须给出模拟所需的基本参数,本实验中使用的基本参数如表1所示.
使用文中第二部分所述的柔版印刷模型对印刷过程中油墨的自由表面变化情况进行分析,利用仿真软件XFlow取微单元化的梯形槽进行处理,如图5.

图5 柔版印刷仿真示意图
如图5(a)所示,油墨在排空力的作用下被挤压到间隙中,且这个填墨区在网纹辊与印版接触点的前方;如图5(b)、5(c)所示,油墨球形分子颗粒形成液膜薄层的凹面曲率随着球体分子润湿性能影响而增加,与空气分子接触的最外层单层球形颗粒之间毛细作用力亦随之增加,液滴内部受到的毛细压力差增加,液体的流动加剧,且拉丝点逐渐后退;如图5(e)所示,在网穴离开的过程中,网孔中的油墨受到网穴的黏附力和油墨分子之间的表面张力作用,油墨部分滞留在网穴中;如图5(g)、5(h)所示,由于法向毛细力造成油墨拉丝纳微系统的黏附失效[14-15],油墨最终在网穴后侧下方发生断裂,然后油墨表面开始流平,形成印刷线条.

图6 接触速度对印版受力的影响
为了研究油墨转移量与网纹辊接触速度的关系,在总填墨量不变的基础上,改变接触速度的大小,观察印版所受力的动态变化,在转移过程完成后稳定状态的受力主要为油墨的压力,便可以知道油墨转移量的变化趋势.假设印刷过程中印版受力均匀,分别仿真求解不同网穴接触速度为:1,20,50,80 mm/s下的印版所受压力,可得趋势图6.
由图6可知,随着网穴接触速度的增大,印版受力逐渐减小即转移墨量减少,即随着接触速度增大转墨量呈减少趋势,仿真结果与Darhuber[16]的结果基本吻合.在速度处于1~20 mm/s时,油墨转移量受接触速度影响较大,所以油墨转移在较小速度状态下对接触速度比较敏感.
4 结论
本文以柔版印刷油墨转移模型为研究对象,通过数学模型的建立对油墨转移过程中的速度、压力、黏性力因素进行了研究,并利用计算流体力学软件XFlow建立了三维的柔版印刷仿真模型,采用流体体积函数模型对自由界面进行追踪,明确了柔版印刷过程中油墨转移情况,得到的主要结论如下:
(1)明确了柔版印刷过程的油墨转移机理,并基于润湿理论和自由表面效应对油墨从网穴中转移到印版上的过程建立了数学模型.
(2)不同网纹辊接触速度下,油墨扩散速度呈现两种不同的状态.在速度较低时,压差是驱动液体流动的主要动力;在高速状态下,辊筒之间间隙变形挤压为驱动液体流动的主要动力.
(3)建立了三维的柔版印刷仿真模型,发现填墨区在版辊接触点的前方,随着网穴移动,油墨最终在接触点后方发生断裂.
(4)利用所建立的三维仿真模型对网纹辊接触速度对油墨转移量的影响情况进行了数值模拟,结果表明,随着速度的增加,拉丝逐渐变长,转移量在模拟速度数值范围内呈线性关系且在速度数值较小的范围内变化时对转移量的影响较大.

