基于双谱和谱特征的心电信号分类方法

刘 姝，邵 杰，张颐婷，张善章

(南京航空航天大学 电子信息工程学院,江苏 南京 211106)

据世界卫生组织(World Health Organization, WHO)统计，因心血管死亡的人数疾病占了全球死亡人数的1/3，且呈现逐年增加的趋势。心血管疾病已逐渐成为危害人类生命的最常见疾病之一[1]。有效地诊断和预防心血管疾病已成为当今医学界面临的重要问题。心电(Electrocardiogram，ECG)信号不仅可以用来分析和鉴别心律失常、心肌梗死等多种疾病，还可以反映心肌细胞损伤程度、发育过程、心房和心室功能结构[2]，是心血管疾病诊断中一种简明有效的工具。

双谱作为一种成熟的信号方法，能够有效抑制高斯噪声带来的干扰，在许多领域得到了广泛应用[3]。然而，由于双谱矩阵较为复杂，目前大多数算法是在得到双谱矩阵的基础上进一步降维提取特征，例如围线积分[4]、双谱切片[5]、主成分分析(Principal Component Analysis，PCA)[6]、独立成分分析(Independent Component Analysis，ICA)[7]、核鉴别分析方法如核主成分分析(Kernel Principal Component Analysis，KPCA)[8]等。

本文引入的算法在双谱矩阵上直接提取二维谱特征对心电信号进行分类识别，不仅实现了有效的特征提取，也提高了识别率，降低了计算量。

1 原理

ECG信号的分类识别过程主要包括4个步骤：(1)对ECG信号进行预处理；(2)计算ECG信号的双谱；(3)通过双谱矩阵提取二维谱平坦度、二维谱亮度以及二维谱滚降度3个特征，并组成特征向量；(4)针对特征向量使用基于径向基函数(Radial Basis Function，RBF)核的支持向量机(Support Vector Machine，SVM)进行分类识别。

1.1 预处理

通常需要对现有数据库中的ECG信号进行去噪和分段，即使用多种滤波器去除信号中的噪声并分离出单个心拍。

1.2 双谱

理论上，双谱可以完全抑制高斯有色噪声的影响，具有高阶谱的时移不变性、相位保持性和尺度变化性等特点。计算双谱时，一般可以采用参数化和非参数化两种方法。其中非参数法比较简单，也可以保证较高的分辨率和较低的估计方差。非参数化的估计方法又包括了直接法和间接法。本文主要采用非参数化的直接双谱估计方法，也就是在得到信号的离散傅里叶变换(Discrete Fourier Transfarm,DFT)系数之后，对该系数作三重相关，得到信号的双谱估计[3]。

假定一段长度为N的观测数据{x(1),x(2),…,x(N)}，采样频率为fs，总的频率采样数即FFT点数是N0，双谱区域内沿水平和垂直方向上的频率采样间隔Δ0=fs/N0。本文中采用的算法步骤为：

步骤1将数据序列平均分成K段，此时每段中包含M个样本，对每段数据去均值处理，生成样本{x(k)(1),x(k)(2),…,x(k)(M)}，其中k=1,…,K。相邻的两段数据之间重叠率为α(%)；

步骤2计算DFT的系数

(1)

其中，{x(k)(n)}是第k段数据，n=1,2,…,M。

步骤3计算DFT系数的三重相关函数

(2)

其中，k=1,…,K；0≤λ2≤λ1；λ1+λ2≤fs/2；N0和L应满足M=(2L1+1)N0；

步骤4得到K段数据双谱估计后，用它们的平均值来表示初始序列的双谱估计

(3)

式中，ω1=2πfsλ1/N0；ω2=2πfsλ2/N0。

1.3 谱特征

普通双谱矩阵是二维数组，包含很多冗余信息，直接用于识别分类会增加分类的难度和计算量。因此，许多研究者使用多种方法对双谱特征进行降维，将二维双谱数据变换为一维谱来提高运算速度。这样虽然后续运算简单，但是降维本身就是一步计算的过程，并且步骤中容易忽略掉一些有用信息。本文直接在双谱矩阵上提取特征，使用的谱特征包括谱平坦度、谱亮度和谱滚降度3种[9]，并由一维扩展到二维。

1.3.1 谱平坦度

谱平坦度测量的是信号谱与噪声谱的接近程度，由谱的几何平均值与算术平均值之比给出。由此可以得到二维欧式空间中谱平坦度的计算式为

(4)

式中，s(i,j)代表的是点(i,j)处的谱幅度值；N是双谱矩阵的点数。由式(4)可得，当谱平坦度接近0时，表示功率集中在少数频段。当所有谱带中功率的分布相似，比如完全平坦谱，那么谱平坦度值为1，此时的信号即为白噪声。

1.3.2 谱亮度

信号的谱亮度可以表示为给定边界频率F以上的谱强度之和与谱总强度之比。推广到二维空间时，可得到式(5)。

(5)

由式(5)可知，谱亮度的值越大，说明在给定频率范围内的能量越多也越集中。

1.3.3 谱滚降度

谱滚降度也是一个对应于边界频率F的函数，可用作测量信号不均匀性的倾斜度。根据信号的特性，在二维域定义如下

(6)

这里β是系数，本实验中经过多次实验，选择为0.3。

2 实验结果分析

2.1 实验数据选定和预处理

本实验中，数据来自美国麻省理工学院提供的MIT-BIH心律失常数据库，这是国际公认的标准数据库之一。被记录者具有不同性别，且来自不同年龄段，因此更具代表性。数据库中一共48条记录，本文采用其中通过修正肢体导联II(Modified Limb Lead II ，MLII)的记录，每条记录时长约为30 min，采样频率为360 Hz。根据美国医疗仪器促进协会(The Association for the Advancement of Medical Instrumentation，AAMI)标准，将数据分为N类(正常或者束支传导阻滞节拍)、S类(室上性异常节拍)、V类(心室异常节拍)、F类(融合节拍)和Q类(未能分类的节拍)等几类。由于Q类数据量过少，此处只讨论数据量比较多的4类[10]。

心电信号极易受到噪声干扰，包括工频干扰、基线漂移，低频和高频噪声等[11]。因此，需要对信号进行预处理。分别使用中值滤波器去除基线漂移，用低通滤波器去除工频干扰和工频噪声，用高通滤波器去除低频干扰，之后使用小波方法寻找信号QRS复合波中的峰值R波位置[12]。以峰值点为原点，该点和之前以及之后各取100个数值，形成长度为200点的单位心电信号片段，共75 604条数据。

2.2 ECG信号的双谱

直接双谱估计算法受多个参数影响，包括每段数据包含的点数记作M，相邻两段数据之间的重复度α以及FFT运算的点数N0。其中点数M与N0存在一定的联系，即M=(2L1+1)N0，L1为任意自然数。信号双谱随不同的M和α参数值而变化。本文选择N0=128，α=50作为双谱计算时的FFT点数和重复度。上文所述4种类型ECG信号的归一化频率的双谱等高线图如图1所示。这4种类型ECG信号分别来自第100、232、208、213号数据。

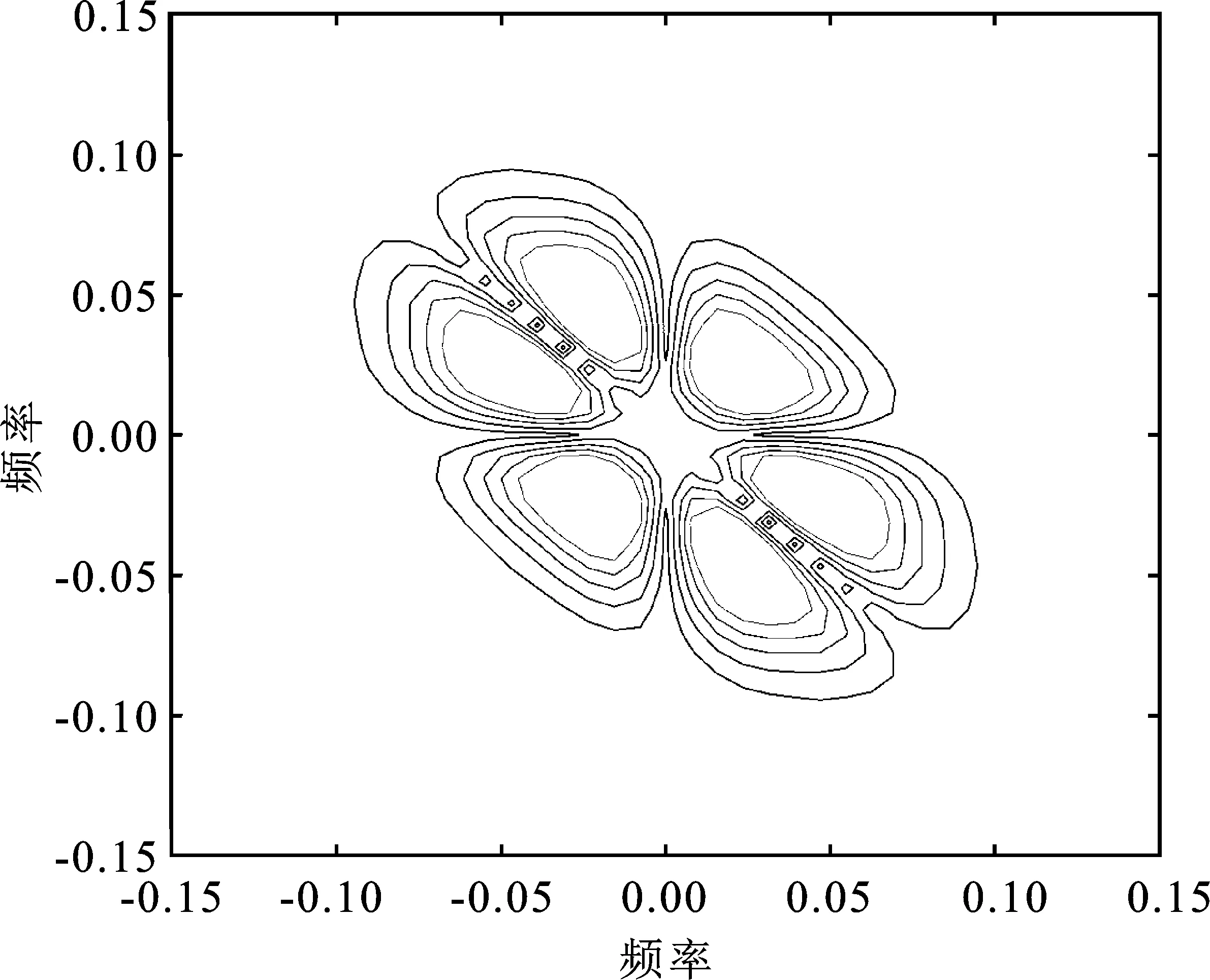
(a)

从图1中可以看出，4种类型ECG信号的双谱等高线图之间差异较为明显。图1(a)的N类和图1(b)的S类即使在频率归一化之后依然在比较大的一个区域内有取值。从内部结构看，图1(c)的V类最为复杂，图1(d)的F类最为简单。由图可知，4种类型ECG信号的双谱图之间的可区分度较高。

2.3 谱特征获取

在双谱矩阵的基础上，直接提取二维谱特征。如图2所示分别是3种谱特征分布的箱型图。共75 604条数据，其中N类67 994条，S类2 577条，V类4 249条，F类784条。

图2中，矩形框外的两条横线分别代表最大值和最小值，框内横线表示中值，矩形框代表上下四分位数之间的区域，框外的加号代表系统判定的异常值。从图2可以看出，对于4类信号，使用二维谱特征是有一定区分度的，尤其是F类信号。S类相对于N类信号，异常值比较多，方差比较大。对应于V类信号的谱平坦度和谱亮度箱型图上下四分位数之间的范围最宽。在图2(c)中，N类信号的谱滚降度大多分布在28和29，后3类信号的谱滚降度分别集中于29、30和31。

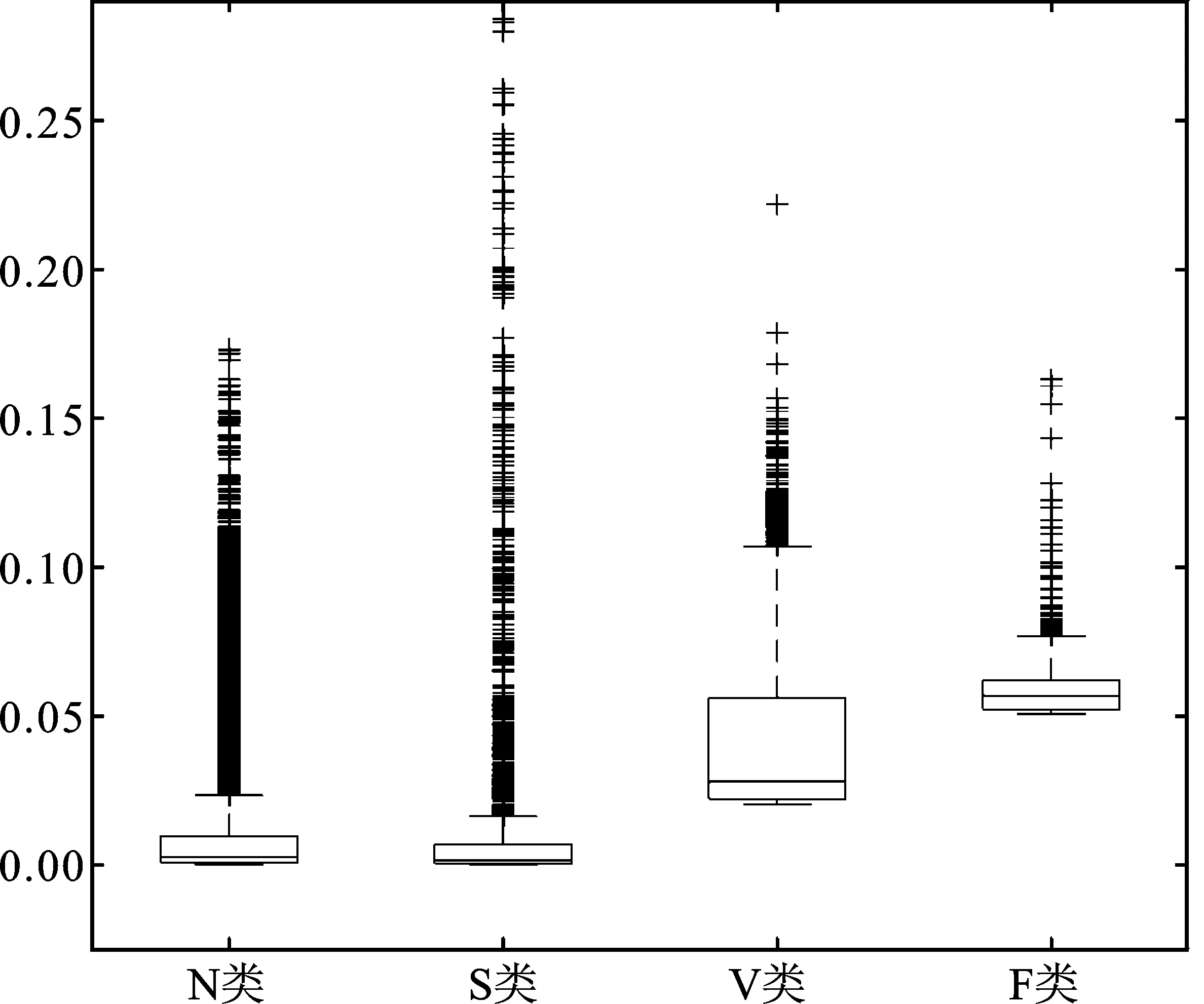
(a)

2.4 分类识别结果

将包含4类ECG信号的样本随机等分成两份，50%用于分类器训练，50%用于性能测试。将3种谱特征构成特征向量,使用RBF-SVM[13]进行分类识别。分类结果如表1所示。

从表1结果可见，4类ECG信号基本得到正确识别，准确识别率约为90%。但是正常心电信号，也就是N类信号样本量过大，对其余几类信号分类效果产生了较大影响。所以，在去掉N类信号后，重复以上实验步骤，得到的分类结果如表2所示。

表1 对N、S、V、F 4类信号分类矩阵

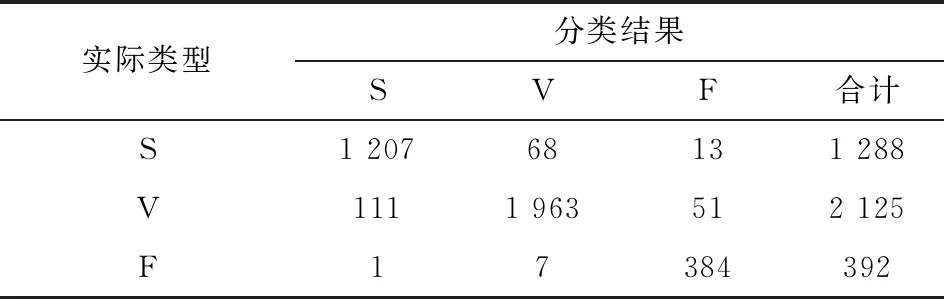
表2 对S、V、F 3类信号分类矩阵

表3是在表2条件下总识别率与其他文献的对比。

表3 本文所提出算法与其他算法比较

从表2和表3可以看出，仅考虑S、V、F 3类信号时，此时ECG信号的识别率达到了93.4%，超过了文献[14～17]中的分类识别效果，与文献[18]相比，低了1.7%。但是在文献[18]中，用于训练的样本数占总样本的80%，测试集仅为20%。这样不仅增加了计算量和时间，也无法在足够多的样本上验证算法的有效性。

表3的识别率结果表明，使用双谱矩阵直接提取的二维谱特征对心率失常信号进行分类识别是有效的。

3 结束语

本文介绍了一种在双谱矩阵基础上直接提取二维谱特征的信号处理方法，并将其结合RBF-SVM以实现心电信号分类识别。实验结果表明，本文提出的双谱和谱特征相结合的特征提取方法既能充分利用高阶谱分析的优良特性，又具有计算量较小、准确度高的特点，是一种有效的ECG信号特征提取方法，为进一步提高ECG信号分类效果和心血管疾病的诊断提供了参考探索。除了MIT-BIH心律失常数据库，还可以通过更多的数据库或临床心电信号数据作进一步的研究和验证，以实现心电信号的自动分析与检测。