微纳卫星在轨温度场快速分析
李志松,马昌健,毛云杰,郭 涛,汪 行,牟旭娜
(1. 上海卫星工程研究所,上海 201109; 2. 上海航天技术研究院,上海 201109)
0 引言
微纳卫星具有体积小、重量轻、结构简单等优点,其研发周期短,经济成本低。随着外形尺寸的缩小,卫星的体积比表面积缩减得更快;如果器件的密度变化不大,则微纳卫星自身的热容和热惯性将随着整星质量的下降而减小。因此,微纳卫星比普通大中型卫星更容易受到内、外热流的影响而出现温度波动[1]。
传统的卫星热设计方法从平台整体到局部单机的建模和仿真分析,细节繁多而复杂,并不适用于微纳卫星快速设计的思路。因此,有必要针对微纳卫星开发新的简化热分析方法。Tsai[2]总结了一系列的卫星热分析数学模型,将现有的热分析模型划分为通用型和简化型:通用型的分析模型过于复杂,难以应用于概念设计、迭代优化和地面测试模拟等阶段;而简化型的分析模型仅考虑辐射传热,精度无法满足工程设计的需要。Totani 等[3]综合了辐射热传递和单个零部件内的传导热传递两方面因素,提出了单节点和双节点的微纳卫星简化热分析数学模型,且计算结果对比表明,双节点模型能达到与多节点模型类似的计算精度。Reiss 等[4]指出,对于目前高度模块化的微纳卫星,热分析模型对于不同的微纳卫星应该具备大部分重用的能力,而无须对每个型号都建立一个新的模型。此外,Elhady[5]在其微型卫星设计研究中指出,接触热传导也是热控系统设计中重要的影响因素。
在现有的热分析商业软件中,基于蒙特卡罗光线追踪方法的角系数计算消耗了很大的建模和运算工作量,而微纳卫星上规则分布的电路板叠层有利于简化星内热辐射中角系数的计算,可大幅提高建模和仿真的效率。
本文将综合内、外热流,内、外辐射及接触导热等因素,以集总参数法对微纳卫星上的各主要部件进行建模,通过有限复杂度的热网络节点的构建来完成整星的热分析,以期快速实现热控设计,并确保模型具有较好的通用性。
1 理论方法
1.1 轨道参数分析
在卫星外热流的计算中,为确定卫星的光照条件,首先要确定卫星的运行轨道情况。以轨道6 根数(半长轴a、偏心率e、倾角i、升交点赤经Ω、近地点幅角ω、真近点角θ)作为输入条件[6],需要求得卫星轨道的周期T0,运行周期内的真近点角θ及其对应时刻t,每个轨道周期内卫星进、出地影时的真近点角θ1、θ2及其对应时刻t1、t2,以及卫星-地心连线与太阳光线之间的夹角ρ。再结合卫星的形状和姿态信息,就可以确定星上各表面的外热流情况。在短期的分析里,不考虑轨道升交点赤经和近地点幅角的摄动变化,也不考虑轨道倾角和偏心率的摄动变化。根据开普勒第二定律,设卫星过近地点的时刻为t0、轨道周期为T0,可求得在半个周期内任一时刻t与真近点角θ之间的对应关系为

计算卫星表面的太阳外热流时,需要确定太阳光照与卫星运行轨道之间的关系,2 个关键的参数是太阳光线与轨道面的最小夹角β(可以看作卫星轨道平面与黄道平面之间的夹角)和轨道近地点与日-地连线之间的夹角Λ。Λ作为轨道近地点到会日点的地心角距,Λ-ω相当于会日点从升交点起量得的地心角距(幅角),Λ+θ相当于卫星在轨道面上与会日点之间的地心角距,如图1 所示。

图 1 Λ 角示意Fig. 1 The Λ angle
对Λ值的求解,可以利用Cunningham 的坐标转换方法[7]。相对于以赤道平面为XY平面、春分点方向为+X轴、地球北极方向为+Z轴的不转动的地球坐标系,设太阳在给定时刻的等效位置坐标为[XS,YS,ZS],根据太阳所在的赤经ΩS和赤纬δS,可以算得:
可以确定在该地球坐标系中,日-地连线的单位矢量为[SX,SY,SZ],其中:
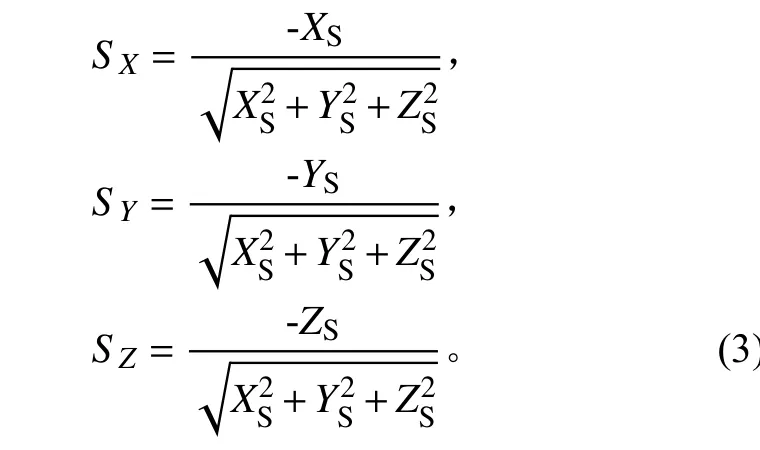

图 2 坐标变换示意Fig. 2 The coordinate transformation
利用Ω、ω和i所确定的空间对应关系,对XYZ坐标进行转换,可以得到一个以地心为原点、卫星轨道平面为xy平面、地心指向卫星近地点方向为+x轴的新的地球坐标系(如图2 所示)。
在新坐标系中,日-地连线的单位矢量为[Sx,Sy,Sz]。新旧坐标间的转换关系为
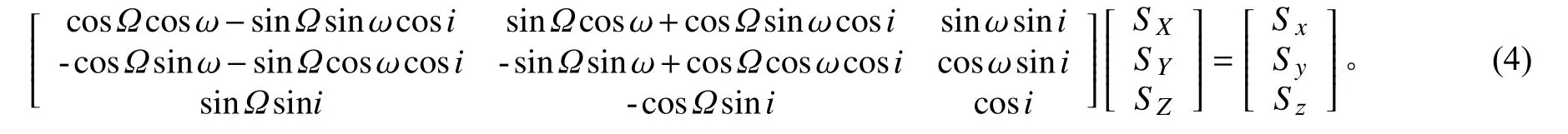
根据Sx和Sy的值,按具体情况选取Λ的角度为0、π/2、arctan(±Sy/Sx)或π-arctan(±Sy/Sx)。获得Λ值以后,可以算出在真近点角θ,卫星-地球连线与太阳光线之间的夹角ρ(相角,取0≤ρ<π)为
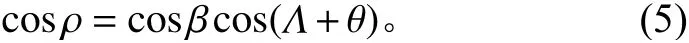
对卫星进、出地影的计算,当Sx和Sy均为0 时,β=π/2,卫星在整个轨道周期内均接受太阳外热流;其他情况下,β范围设为0~π/2,计算式为
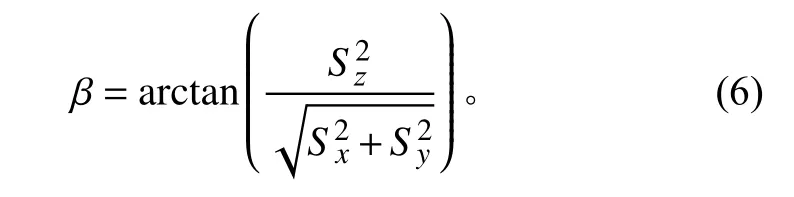
假定地球的阴影区为一圆柱体空间,卫星轨道平面与该圆柱体空间相交的区域为半个椭圆面,则该椭圆的半短轴为地球半径RE、半长轴为RE/sinβ,不考虑卫星轨道非常高和位于半阴影区时的情况。卫星进、出地影的具体时刻主要通过Sx、Sy和卫星所在位置的真近点角θ来判断[8],当阴影函数
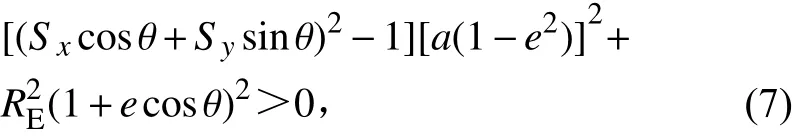
且其中的(Sxcosθ+Sysinθ)>0 时,即认为卫星处于地影之中。
1.2 外热流计算
卫星外热流计算主要包括太阳辐射、地球红外辐射和地球反照,暂不考虑卫星自身对外热流的二次辐射。
在地球附近,太阳辐射强度可以表示为
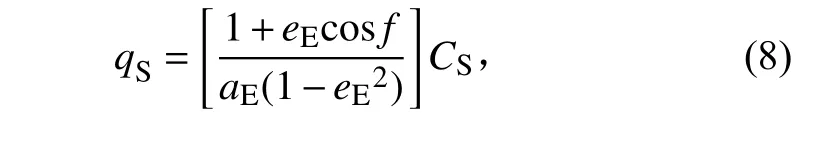
式中:aE为地球与太阳之间的平均距离,即1 个天文单位(AU);eE为地球绕太阳运行的轨道偏心率;f为太阳在天球坐标系中的真近点角;CS为太阳常数。
地球红外辐射所产生的外热流为

式中FE为地球与卫星之间的角系数。
仅考虑卫星运行在光照区内和轨道高度不太高的情况,地球反照的热流密度为
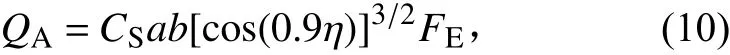
式中:定义(ab)为地球反照系数,由地球反照角系数和地球反照率共同决定,计算中取其值为0.35;η为卫星-地心连线与太阳光线之间的夹角,与ρ一致,系数0.9 是考虑了当卫星-地心连线与太阳光线之间的夹角超过π/2,但仍然可能受到地球反照的情形。
式(9)、(10)中,FE的近似拟合计算式[9]为

其中:λ为卫星的某个表面相对于卫星-地心连线(天顶方向)的夹角,例如对地定向的卫星,其对地的那一面的λ值恒为π;r为地球半径RE与卫星到地心距离(RE+h)之比,即

S的拟合经验表达式为
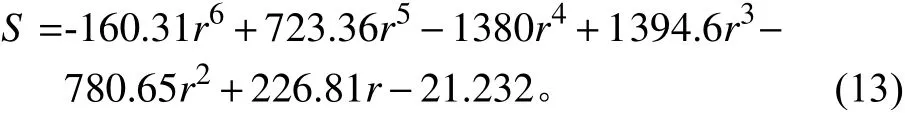
根据以上的理论和近似分析结果,可在MatLab SimuLink 中建立模型,计算外热流随卫星真近点角的变化。
微小型卫星多采用六面体外形,其姿态控制采用三轴稳定并对地定向时,假定+X面为指向飞行方向,+Z面指向地心,+Y面的方向通过右手定则确定。以此卫星质心为坐标系原点,卫星指向地心的单位矢量为[0, 0, 1]。卫星姿态发生变化时,假定偏航角为φ,俯仰角为γ,滚动角为φ,其姿态矩阵为
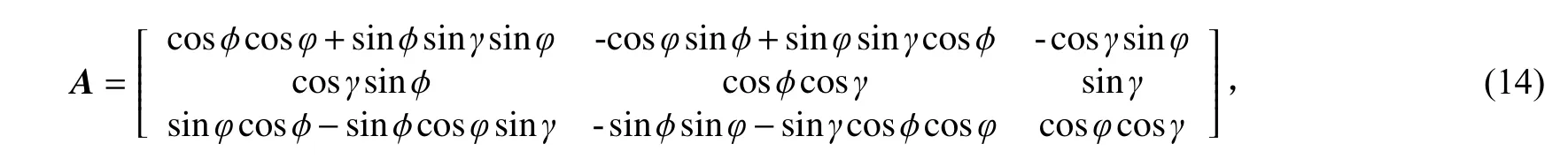

到达该平面的太阳辐射热流为Ei=CScosζ。
根据以上论述,在加入卫星的姿态角信息以后,可以获得外形为六面体的卫星各面上所受的外热流的值Ei。
1.3 卫星温度场计算
卫星温度场的确定,除了轨道外热流的计算,还需考虑卫星内外表面的吸收与反射,星内热源以及卫星内部的辐射、传导等耦合传热关系。针对小型卫星的结构和布局特点,其整体温度场可采用整星的热平衡方程进行分析,即
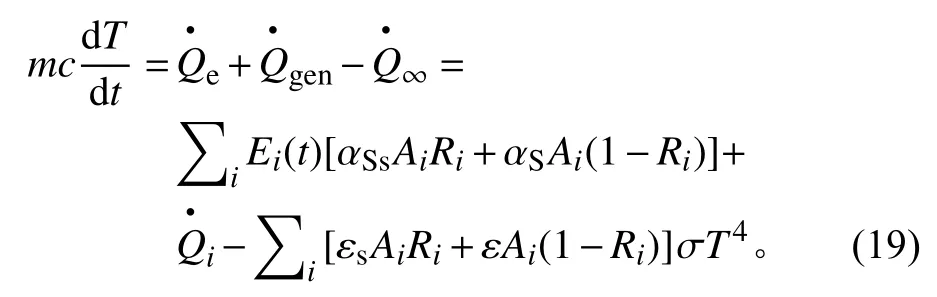


在前面的论述中,外热流Ei是轨道真近点角θ的函数。而式(1)中轨道真近点角θ却是时间t的隐函数,从任意t求出对应的θ需要采用数值方法。因此,Ei难以表示为时间t的函数。现有的一个解决方法[3]是,先将轨道按真近点角θ从0 到2π平均细分成很多份(如8000~10 000 份);然后将各θ值与具体的时间点t以及对应的Ei通过列表进行记录,从而得到离散的Ei(t);最后对t进行数值积分,以求出温度T的变化。这种方法虽然可行,但是操作烦琐,难以对任意参数的轨道进行自动求解,且计算精度受到细分份数的限制。本文提出一个简单的连续积分的方法,在式(1)的两端对t求导,可以求得
从而能够通过对θ求积分,求出整星温度T随真近点角θ变化的情况。通过θ与t之间的连续对应关系,可获得温度T随时间t变化的连续曲线。
2 算例
目前大量的微纳卫星采用了如图3 所示的印制电路板-机箱式结构布局,内热源的分布较大中型卫星更为简单和规律化,使得采用集总参数法进行简化分析成为可能。设:微纳卫星对地定向,偏航角、俯仰角和滚动角均为0,几何外形为正六面体,尺寸为0.3 m×0.3 m×0.3 m,单个外表面的面积A为0.09 m2,整星质量m为15 kg,整体比热容c为720 J/(kg·K),星内热源Qi为50 W;各表面上铺设太阳电池的面积比为0 或0.6,太阳电池的太阳吸收比αSs为0.92、发射率εs为0.85;卫星各部件的初始温度均为20 ℃(293 K)。

图 3 典型微纳卫星的内部结构Fig. 3 Typical internal structure of a nanosatellite
设微纳卫星外壳为铝合金蜂窝板,厚0.015 m,单个面板面积较小,面内近似等温。星内热源主要在印制电路板上,发热元器件通过电路连接和导热硅橡胶等与电路板整体形成热耦合,故可近似认为电路板本身就是均温体热源,从而假定每片电路板就是热网络中的一个节点,并可进一步简化为没有厚度的薄平板。各平板相互平行,面积相等,间距远小于板长和板宽,板与板和板与卫星外壳之间的辐射及传导换热可通过分析的方法求解。卫星的六面体外壳可以进一步分解为6 个单独的外壳节点。按电路板堆叠分布的特点,假设前方的外壳板仅与排列在最前方的电路板和四侧的外壳板换热,后方的外壳板仅与排列在最后方的电路板和四侧的外壳板换热。并假设,6 片外壳板之间的相互接触热传导很弱;正前方、正后方的外壳板不与侧面的4 片外壳板辐射换热,同时由于电子元器件的遮挡,4 片侧面外壳板之间也不考虑互相辐射换热。星上各部件之间的辐射换热,其角系数可以通过理论公式[10]算出。假设星内有5 片大小相同的电路板,均与X轴垂直,正面均为单一朝向,则整星的传热关系可以等效于图4 所示的部件节点划分和图5 所示的热网络节点及热阻关系。将整星连同宇宙空间共划分为16 个节点和40 个热阻关系,在SimuLink中进一步构建数学模型求解。
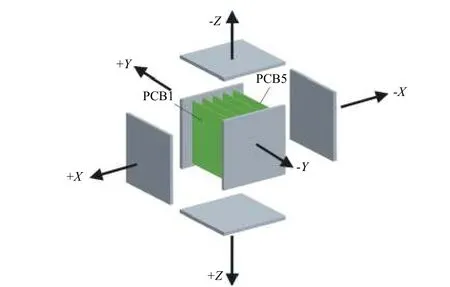
图 4 微纳卫星上等温化假设的简化部件Fig. 4 The simplified isothermal components of a nanosatellite
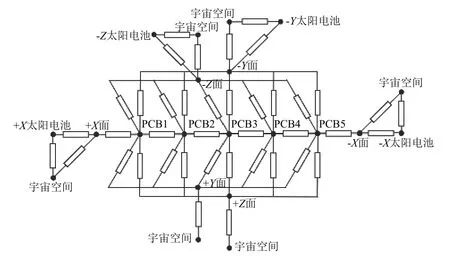
图 5 多节点热网络节点及热阻关系Fig. 5 The multi-nodal network of thermal resistances
图5 的热网络中存在一系列的传导热阻需要进行计算评估。卫星通过聚酰亚胺(PI)薄膜隔热,各接触面用硅橡胶粘贴太阳电池片,故其总传热系数U可以估算为
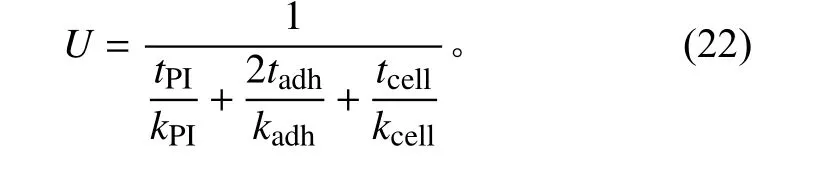
式中:t为厚度,聚酰亚胺薄膜厚度tPI设为1.0 mm,硅橡胶涂覆厚度tadh设为0.08 mm,太阳电池片厚度tcell设为1.5 mm;k为热导率,kPI约为0.12 W/(m·K),kadh约为0.39 W/(m·K),kcell约为14 W/(m·K)。
据此估算的传热系数约为1653 W/(m2·K),对于0.054 m2大小的面积,其热阻仅约0.011 2 K/W。因此可以认为太阳电池片与外壳是接近等温的,在分析中可作为同一节点处理,总节点数可由16 个减少到12 个。电路板相邻间距设为0.05 m,相互之间的导热连接主要依靠电连接器、支撑柱和在卫星壳体上固定点,相邻两片电路板之间的传导热阻估算为2.32 K/W。电路板与±Y面和±Z面的外壳接触固定,根据国外的经验数据,每片电路板与外壳面板之间的热阻设为1.4 K/W。非相邻的电路板之间,以及电路板与没有接触固定的外壳面板之间不考虑直接热传导。
各节点的热物理性质[11]和建模参数如表1 所示。表中带上划线的为面内平均值。
基于以上设定,对于星内各节点的温度变化,可以计算如下:
对于电路板节点,



3 算例结果与讨论
在此,以常见的800 km 高度太阳同步轨道和地球同步轨道为例。两轨道偏心率均为0.0,太阳同步轨道的倾角为95.597°、半长轴为7178 km,地球同步轨道的倾角为0°、半长轴为42 164.17 km,初始真近点角均取为0°。在春分日,两个轨道的外热流分别如图6(a)、(b)所示。为了对建模计算结果的正确性进行校验,图6 还给出采用Thermal Desktop 5.0商业软件的仿真数据进行对比,假设表面太阳吸收比为1。可以看到,建模计算结果与软件仿真数据在具体的热流强度和进入地影时刻等方面均符合良好;在最大热流密度方面两者稍有偏差,应该是计算时太阳常数的设置存在差异所致。

图 6 春分日六面体卫星各面所受轨道外热流随真近点角变化的情况Fig. 6 The external heat flux vs. the true anomaly for each surface of an orbiting hexahedron satellite
分别对高温工况和低温工况进行热控设计数值模拟评估,模拟结果如图7 和图8 所示。轨道参数依照前述的太阳同步轨道设置。
由图7 可见,高温工况(星上热源全部启动)下,由于初始温度比较接近稳态值,卫星在经历了约4 个轨道周期后就基本达到稳定的温度循环。图7(a)显示,各外壳面板之间温度差异较大。这是由于,±Y和±Z面与星上载荷(电路板)有热耦合,且面外侧做了隔热多层和喷漆等热控设计,加之地球红外辐射和反照的影响,使得这些面的温度波动较小(13~35 ℃);而±X面受外热流影响较大,且与卫星内部热耦合程度不高,故温度变化剧烈(-10~75 ℃)。图7(b)显示,星内各电路板间温差较小,在卫星外壳遮挡和内部热耦合的作用下,平均温度约为22 ℃,在1 个轨道周期内的变化范围仅约15 ℃,有利于电路板上电子设备的可靠工作。

图 7 高温工况下卫星各部件温度随时间的变化Fig. 7 Temperature vs. time for each satellite component under high temperature condition
由图8 可见,低温工况(星上热源全部关闭)下,从初始到稳态的温度差距较大,卫星实现稳定温度循环所需的时间较长,约为8 个轨道周期。各面板的温度波动现象与高温工况类似,但温度下降,星内平均温度维持在-25 ℃左右,轨道周期内变化范围也约15 ℃。通过与Thermal Desktop 5.0 的仿真结果进行对比,可以发现本研究之建模计算的瞬态温度曲线在时间和变化趋势上与仿真结果吻合良好,温度值的最大偏差仅约2~3 ℃,表明建模计算的精度已可满足工程应用的需求。建模计算与仿真结果间的差异主要表现在电路板的温度预测上,其原因是星内的热耦合建模较为简化,一些辐射换热关系被忽略,不如Thermal Desktop 5.0 中的详细完整。若模型内继续添加热网络内各节点间的换热关系细节,则计算精度有望进一步提高。

图 8 低温工况下卫星各部件温度随时间的变化Fig. 8 Temperature vs. time for each satellite component under low temperature condition
4 结束语
本文在分析微纳卫星热控系统需求特性和结构布局特点的基础上,对一般性椭圆轨道卫星的外热流进行建模,并利用集总参数法建立微纳卫星的简化多节点分析热阻网络模型。在建模过程中,突破了卫星进入地影、热平衡方程对真近点角变化的连续积分和星内热耦合分析等技术问题。该热阻网络模型与真实的微纳卫星具有较高的热物理相似性,其对卫星的高温和低温工况计算示例结果与专业航天器热分析软件的仿真数据对比显示,该模型能有效预测轨道外热流和卫星的瞬态温度场,并具有较好的精度,而计算耗时仅为几秒钟。该分析模型可以根据用户的具体需求选择不同的轨道参数,调整卫星的外形尺寸、飞行姿态、电路板数量、热负荷工况以及各部件的热物理性质。在现有模型的基础上,还可以进一步细化结构,如加入连接各外壳面板和电路板的金属框架,通过固体导热提升系统整体的等温性等,而数学模型本身的复杂程度不会大幅增加。因此,该模型将是微纳卫星研制过程中实现热控设计快速迭代优化和方案比较评估的有力工具。

