基于STM32低轨卫星轨道预报系统研究与设计
何建 旷小兵

【摘要】 在低轨卫星过顶时间段内,卫星地面站根据轨道预报完成自动跟踪才能实现与卫星通信。针对轨道预报需要,提出了一种基于STM32单片机卫星轨道预报系统平台。将轨道预报算法进行了嵌入式软件设计,满足于在STM32单片机上运行。该设计在保证轨道预报精度情况下,系统平台较传统的轨道预报方法实用性强,简化预报程序和相应的上位机软件, 提高预报效率。
【关键词】 轨道预报 数值积分 卫星轨道根数 STM32单片机
引言
在低轨卫星过顶这段时间内,卫星地面站处于低轨卫星天线波束覆盖范围内,过顶预报用到的轨道预报算法十分复杂。大都是采用上位机软件进行过顶预报,再将预报结果下发给卫星地面站。这样以来,过顶预报需要人为操作,而且容易出错,预报实时性不高。
为此,本文提出了一种基于STM32低轨卫星轨道预报系统,该系统位于卫星地面站内,只需要将预报卫星轨道根数下发给该系统就能进行实时预报,操作简单、长时间全天候预报,不需要人为干预。
一、系统硬件电路设计
系统硬件电路包括:单片机电路、FLASH存储电路、GPS接收电路、串口接口电路等组成。系统电路框图如图1所示。
该电路以单片机STM32F429ZTI6为核心,主要用于控制整个系统的运行以及星历解算的实现;FLASH存储电路主要用于存储计算章动时需要的DE405星历数据,计算极移和地球自转角时需要的EOP数据,将这些外部数据从得到的原始数据中提取出来,存放在二进制文件中,以提高计算程序的效率;GPS接收电路主要用于接收地面站的位置、速度和时间信息;串口接口电路主要用于将卫星轨道预报结果输出给地面站,接收卫星轨道根数的输入。
二、系统软件设计
系统软件能够根据预先设定的轨道参数实时计算出卫星在WGS-84坐标系下的经度、纬度和高度,结合地面站位置坐标,计算出地面站天线指向卫星的方位角和俯仰角。
2.1数值积分
Cowell法是求解航天器运动微分方程时最为简单的数值积分算法——它直接对运动方程在J2000.0赤道惯性坐标系中的分量形式进行数值积分:
式中:
μ——地球引力常数;
fx、fy、fz——分别为三轴摄动加速度,主要包括地球形状摄动、大气阻力摄动、日月摄动、太阳光压摄动。
2.2地面站天线指向
地面站指向卫星的矢量s在WGS-84坐标系中表示为:
其中:表示卫星在WGS-84坐标系中的位置坐标
表示地面站在WGS-84坐标系中的位置坐标
地面站指向卫星的矢量s在“北-天-东”坐标系中表示为:
地面站指向卫星的矢量s在地面站天线本体坐标系中表示为:
地面站天线俯仰角
地面站天线方位角
2.3系统流程设计
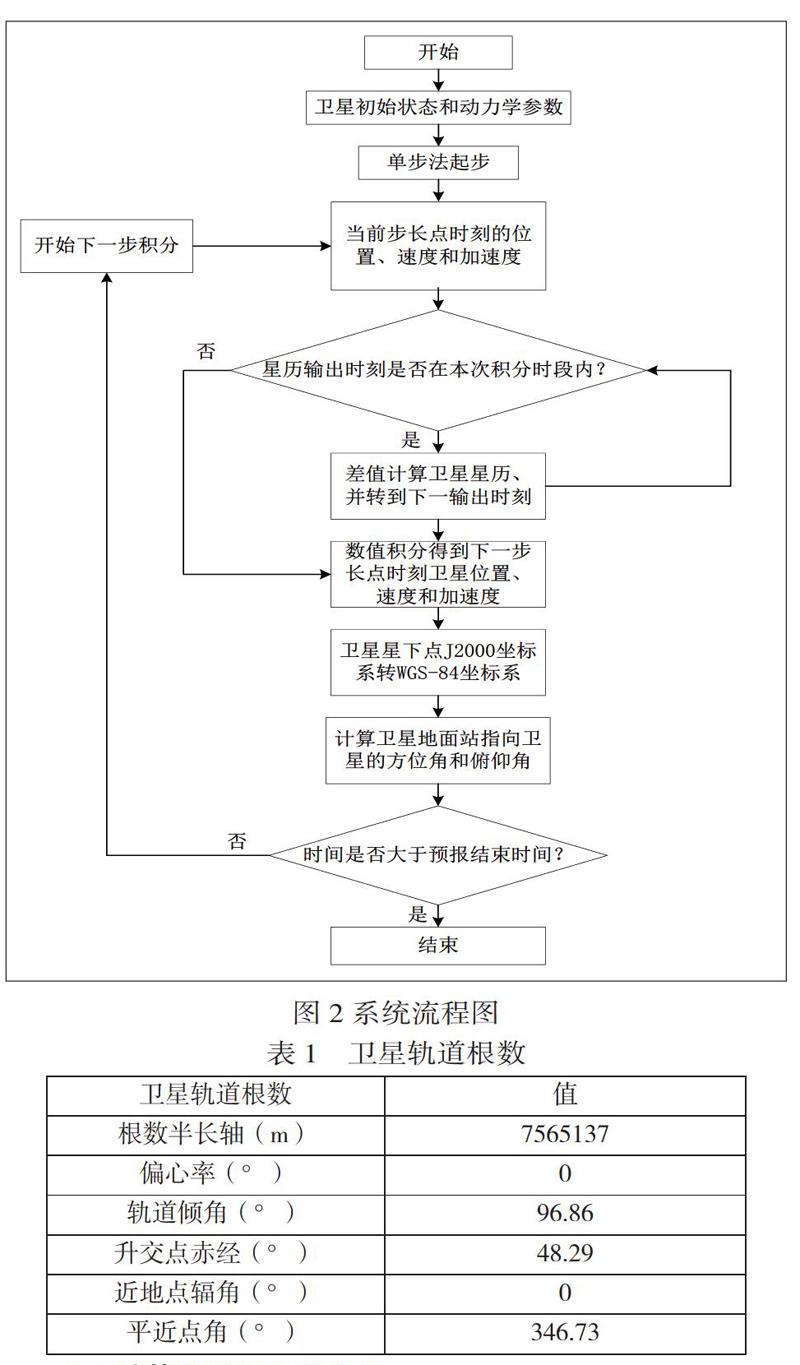
结合卫星轨道预报的输入参数,用单步法起步,开始进行轨道积分并依次计算卫星星历,使用Cowell 数值积分器轨道预报,整个卫星轨道预报具体流程见图2所示。
三、系统验证与分析
3.1 输入数据
以低轨卫星为验证对象,使用美国AGI公司开发的STK(Satellite Tool Kit,卫星工具包)中的HPOP(High Precision Orbit Propagator,高精度轨道预报)模型为验证基准。卫星轨道根数采用表1所示。
3.2计算结果及误差分析
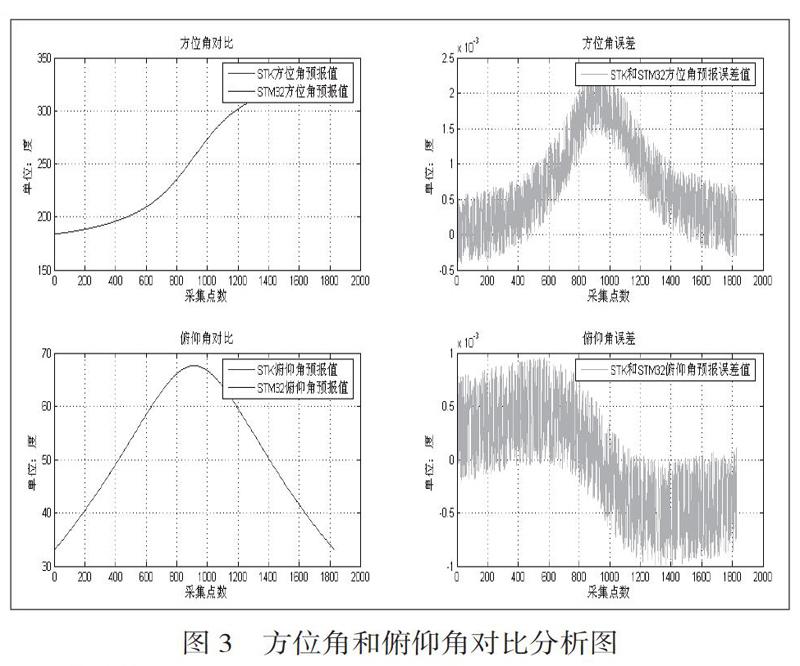
如图3所示,STK与STM32计算的方位角与俯仰角预报值进行对比分析可知,在低轨卫星过顶时间段内,当低轨卫星进入可视范围,方位角180度时方位误差最小为0.2×10-3,俯仰角33度时误差最大为+0.5×10-3;当低轨卫星经过头顶,方位角250度时方位误差最大为2.2×10-3,俯仰角68度时误差最小为0;当低轨卫星离开可视范围,方位角340度时方位误差最大为2.2×10-3,俯仰角33度时误差在-0.5×10-3。方位角誤差在10-3数量级,俯仰角误差在10-3数量级,误差范围很小,满足低轨卫星跟踪需要。
如图4所示,STK与STM32计算的经度、纬度、高度进行对比分析可知,在低轨卫星过顶时间段内,经度误差在10-5数量级,纬度误差在10-4数量级,高度误差在0.1米以内,误差范围很小,满足低轨卫星跟踪需要。
四、结束语
本文设计了一种基于STM32低轨卫星预报系统平台,通过与STK软件中HPOP模型卫星预报数据进行对比分析。分析结果表明,计算结果与STK软件星历预报结果偏差较小,能够满足空间低轨卫星轨迹预报的精度要求。本系统平台较传统的轨道预报方法实用性强,简化预报程序和相应的上位机软件, 提高预报效率。可应用于地面卫星站跟踪卫星目标的需要。
参 考 文 献
[1] 孟祥强,马广彬,黄鹏,等.一种大椭圆轨道卫星星历预报方法[J].飞行器测控学报,2017(3)
[2] 张如伟,刘根友.低轨卫星轨道拟合及预报方法研究[J].大地测量与地球动力学,2008(4)
[3] 雷伟伟,张捍卫,李凯.岁差章动模型更新等因素对坐标转换的影响[J] .飞行器测控学报,2016(01)
[4] 付兆萍,卫星轨道运动方程数值算法研究[D], 华中科技大学硕士学位论文,2006
[5] 王威,于志坚,航天器轨道确定——模型与算法[M].北京:国防工业出版社,2007
[6] 郑慧娆,陈绍林,莫忠息等.数值计算方法[M].武汉:武汉大学出版社,2002
[7]马忠梅等.单片机的C语言应用程序设计[M].北京:北京虹口航天大学出版社,2003

